Capítulo 32 Análisis de componentes principales
José-María Montero\(^{a}\) y José Luis Alfaro Navarro\(^{a}\)
\(^{a}\)Universidad de Castilla-La Mancha
32.1 Introducción
En el estudio de cualquier problema de interés, lo ideal es tomar información del mayor número de variables posible, lo cual, actualmente, no es un impedimento. Sin embargo, trabajar con muchas variables es incómodo (por ejemplo, si fueran 30 y se estuviese interesado en su correlación dos a a dos, habría que calcular 435 coeficientes). Además, tener muchas variables no implica necesariamente tener mucha información. Si están correlacionadas entre ellas (que suele ser el caso en la realidad), parte de la información que proporcionan es redundante. Por consiguiente, el reto es reducir la dimensionalidad del problema sin reducir la cantidad de información proporcionada por las variables originales, midiéndose dicha cantidad de información a través de su variabilidad, en consonancia con el concepto de entropía. En concreto, se adopta como medida de la variabilidad de las variables originales la suma de sus varianzas.
Pues bien, el análisis de componentes principales (ACP, perteneciente al ámbito del aprendizaje no supervisado) es una técnica de reducción de la dimensionalidad, un problema importante en ciencia de datos, tanto en el aprendizaje supervisado como no supervisado. ACP opera sustituyendo las variables originales por un número reducido de combinaciones lineales de ellas, incorrelacionadas, denominadas componentes principales (c.p.), que capturan un elevado porcentaje de la variabilidad de las variables originales (Boehmke & Greenwell, 2020; Hothorn & Everitt, 2014). ACP es el primer intento de reducción de la dimensionalidad y el único utilizado a tal fin hasta el advenimiento del escalamiento multidimensional (aunque no es su función principal) y otras técnicas más complicadas pertenecientes al ámbito del aprendizaje múltiple (manifold learning).
La reducción de la dimensionalidad no solo es útil en el estudio de fenómenos complejos con un elevado número de dimensiones, sino también para facilitar la implementación de otros métodos de aprendizaje no supervisado, como el análisis clúster218 (reduciendo el número de dimensiones a utilizar para configurar los clústeres), o supervisado, como, por ejemplo, la regresión (reduciendo el número de regresores y haciéndolos incorrelacionados, evitando así información redundante y la multicolinealidad); o la técnica de partial least squares (PLS, similar a la regresión con c.p., pero que, en vez de ignorar la variable respuesta en la determinación de las combinaciones lineales, busca aquellas que, además de explicar la varianza de las variables originales, predicen la variable respuesta lo mejor posible).219 También es muy útil para representar gráficamente relaciones multivariantes.
En R hay varias opciones para la realización de un ACP: princomp(), prcomp() y PCA(), de la librería FactoMineR (Lê et al., 2008), entre otras. Se ha optado por la última porque \((i)\) incorpora notables mejoras gráficas; \((ii)\) permite el ACP con missing values, imputando dichos valores (paquete missMDA); \((iii)\) proporciona una descripción e interpretación automática de los resultados, seleccionando los mejores gráficos, mediante el paquete FactoInvestigate; \((iv)\) permite la implementación de técnicas híbridas (por ejemplo, clusterización con c.p.); y \((vi)\) posibilita la predicción de las coordenadas de individuos y variables adicionales utilizando únicamente inputs del ACP previo.
Como ilustración práctica del ACP, se abordará la reducción de la dimensionalidad de un problema del ámbito de la sociedad de la información en la UE-27, en 2021. Se dispone, para 2021 y a nivel de país, de información sobre 7 variables: 4 relacionadas con el uso de las TIC por parte de las empresas y 3 relativas al uso de dichas tecnologías por parte de las personas y a la equipación TIC de los hogares. Dicha información, así como la descripción de las variables, puede consultarse en la base de datos TIC2021 del paquete CDR.
32.2 Obtención de las componentes principales
32.2.1 Descripción formal del proceso
Sea \(\mathbf{X^\prime}=(X_{1},\dotsc,X_{p})\) un vector \(p\)-dimensional de variables aleatorias con vector de medias \(\boldsymbol{\mu}\) y matriz de covarianzas conocida \(\boldsymbol{\Sigma}\). Puesto que los cambios de origen no afectan a la covarianza, las variables originales se consideran centradas, de tal manera que \(\boldsymbol{\mu}=\mathbf {0}\) y \(\boldsymbol{\Sigma}= E\left (\mathbf{X^\prime} \mathbf{X}\right)\). Se trata de encontrar un conjunto de \(p\) combinaciones lineales incorrelacionadas de dichas variables,220 \(Y_{m}=a_{1m}X_{1}+a_{2m}X_{2}+\dotsb+a_{pm}X_{p}=\mathbf{a}_{m}^{\prime}\mathbf{X}, \hspace{0,1 cm}{m=1,2,\dotsc,p}\), denominadas c.p., que recojan la variabilidad existente en los datos. La idea es ordenar las c.p. tal que \(V(Y_1)> V(Y_2)>...> V(Y_p)\), y seleccionar \(k\) de ellas (las \(k\) primeras), \(k<p\), que capturen un elevado porcentaje de la variabilidad de los datos.
Nota
Geométricamente, las c.p. representan un nuevo sistema de coordenadas obtenido mediante la rotación de los ejes originales. Los nuevos ejes representan las direcciones de máxima variabilidad y proporcionan una descripción más simple de la estructura de covarianza.
La varianza de cada componente y la covarianza entre ellas vienen dadas por: \[\begin{equation} \begin{split} Var(Y_{m})=\mathbf{a}_{m}^{\prime}\mathbf{\Sigma}\mathbf{a}_{m}, \quad{\forall m=1,2,\dotsc,p}, \\ Cov(Y_{m}, Y_{s})=\mathbf{a}_{m}^{\prime}\mathbf{\Sigma}\mathbf{a}_{s}, \quad{\forall m, s \{m\neq s\} =1,2,\dotsc,p}. \end{split} \tag{32.1} \end{equation}\]
32.2.1.1 Obtención de la primera componente principal
La primera c.p., \(Y_1\), se obtiene seleccionando el vector \(\mathbf{a}_{1}\) que maximice su varianza. Sin embargo, dado que la varianza de cada c.p. puede incrementarse arbitrariamente multiplicando \(\mathbf{a}_{1}\) por una constante, se impone la condición \(\mathbf{a}_{1}^{\prime}\mathbf{a}_{1}=1\); es decir, se normalizan los vectores, de tal forma que tengan longitud unitaria. Por tanto, se trata de encontrar el vector \(\mathbf{a}_{1}\) que maximiza \(Var(Y_{1})=\mathbf{a}_{1}^{\prime}\mathbf{\Sigma}\mathbf{a}_{1}\) sujeto a que \(\mathbf{a}_{1}^{\prime}\mathbf{a}_{1}=1\). En otros términos, se selecciona el vector \(\mathbf{a}_{1}\) que maximiza el lagrangiano: \[\begin{equation} \mathcal{L}(\mathbf {\mathbf a}_{1})=\mathbf{a}_{1}^{\prime}\mathbf{\Sigma}\mathbf{a}_{1}-\lambda (\mathbf{a}_{1}^{\prime}\mathbf{a}_{1}-1). (\#eq:ecuacion2acp) \end{equation}\] Para ello, se deriva respecto a \(\mathbf{a}_{1}\) y \(\lambda\), y se igualan a cero dichas derivadas: \[\begin{equation} \begin{split} \frac{\partial\mathcal{L} (\mathbf{a}_{1})}{\partial\mathbf{a}_{1}}=2\mathbf{\Sigma}\mathbf{a}_{1}-2\lambda\mathbf{a}_{1}=(\mathbf{\Sigma}-\lambda\mathbf{I})\mathbf{a}_{1}= \mathbf{0}, \\ \frac{\partial \mathcal{L}(\mathbf{a}_{1})}{\partial\lambda}=\mathbf{a}_{1}^{\prime}\mathbf{a}_{1}-1=0. \end{split} (\#eq:ecuacion3acp) \end{equation}\] La primera ecuación tendrá solución distinta del vector nulo cuando \((\mathbf{\Sigma}-\lambda\mathbf{I})\) sea singular; es decir, cuando \(|\mathbf{\Sigma}-\lambda\mathbf{I}|=0\), o en otros términos, cuando \(\lambda\) sea un autovalor de \(\mathbf{\Sigma}\). Dado que,
- \(\boldsymbol{\Sigma}\) es semidefinida positiva y, en general, tendrá p autovalores no negativos,
- y que en el proceso de optimización, premultiplicando \((\mathbf{\Sigma}-\lambda\mathbf{I})\mathbf{a}_{1}= \mathbf{0}\) por \(\mathbf{a}^{\prime}_{1}\) y teniendo en cuenta que \(\mathbf{a}_{1}^{\prime}\mathbf{a}_{1}=1\), resulta que \(\lambda= \mathbf{a}_{1}^{\prime}\mathbf{\Sigma}\mathbf{a}_{1}= V({Y_1})\),221
se seleccionará el mayor de los autovalores de \(\boldsymbol{\Sigma}\), obteniéndose el autovector \(\mathbf{a}_{1}\) de tal forma que cumpla la condición \(\mathbf{a}_{1}^{\prime}\mathbf{a}_{1}=1\).
32.2.1.2 Obtención de la segunda componente principal
\(Y_{2} = \mathbf{a}_{2}^{\prime}\bf{X}\) se obtiene igual que \(Y_{1}\), pero añadiendo la condición de incorrelación con \(Y_{1}\): \(Cov(Y_{1}, Y_{2}) = \mathbf{a}_{2}^{\prime} \mathbf{\Sigma} \mathbf{a}_{1} = 0,\) o equivalentemente, \(\mathbf{a}_{2}^{\prime}\mathbf{a}_{1}=0\) (\(\mathbf a_1\) y \(\mathbf a_2\) son ortogonales).222
Por tanto, el lagrangiano a maximizar es:
\[\begin{equation} \mathcal{L}(\mathbf {a}_{2})=\mathbf{a}_{2}^{\prime}\mathbf{\Sigma}\mathbf{a}_{2}- \lambda (\mathbf{a}_{2}^{\prime}\mathbf{a}_{2}-1)- \gamma (\mathbf{a}_{2}^{\prime}\mathbf{a}_{1}-0). \tag{32.2} \end{equation}\]Derivando respecto a \(\bf{a}_{2}\) e igualando a cero:
\[\begin{equation} \frac{\partial \mathcal{L}(\mathbf {a}_{2})}{\partial\mathbf{a}_{2}}= 2\mathbf{\Sigma}\mathbf{a}_{2} -2\lambda \mathbf{a}_{2}- \gamma \mathbf{a}_{1}= 2(\mathbf{\Sigma}- \lambda \mathbf{I}) \mathbf{a}_{2}- \gamma\mathbf{a}_{1} = \mathbf{0}. \tag{32.3} \end{equation}\]Premultiplicando por \(\mathbf{a}_{1}^{\prime}\) y considerando la condición de ortogonalidad se tiene que \(\gamma=2 Cov (Y_1,Y_2)=0\), con lo que \(\frac{\partial \mathcal{L}(\mathbf {a}_{2})}{\partial\mathbf{a}_{2}}= 2{\mathbf \Sigma}{\mathbf {a}_2} - 2 \lambda \mathbf a_2 = 0\), que implica que \((\mathbf \Sigma -\lambda \mathbf I)\mathbf a_2=0\).
Siguiendo el mismo razonamiento que en la obtención de la primera componente, se elige el segundo mayor autovalor de \(\mathbf\Sigma\),223 \(\lambda_{2}\), siendo \({\bf{a}}_{2}\) el autovector asociado a él.
32.2.1.3 Obtención del resto de las componentes principales
Repitiendo este procedimiento, se obtienen las p c.p., siendo los coeficientes de la j-ésima los componentes del autovector asociado al j-ésimo mayor autovalor de \(\mathbf \Sigma\).
El vector de c.p. se puede expresar como \(\mathbf{Y}=\mathbf{A}^{\prime}\mathbf{X}\), donde \(\mathbf{A} = [{\bf{a}}_{1}, {\bf{a}}_{2},\dotsc,{\bf{a}}_{p}]\) es la matriz de autovectores (ortogonales) obtenidos.
32.2.2 Cuestiones importantes en el análisis de componentes principales
32.2.2.1 Varianza de las variables originales y las componentes principales
La matriz de covarianzas de las c.p., \(\mathbf V(\mathbf Y)=\mathbf A^\prime \mathbf \Sigma \mathbf A\), coincide con \(\mathbf{\Lambda}\), que es una matriz diagonal, puesto que las c.p. están incorrelacionadas y sus varianzas (los valores de la diagonal principal) son los autovalores de \(\boldsymbol{\Sigma}\). En consecuencia: \[\begin{equation} \begin{split} \sum_{m=1}^{p}Var(Y_{m})= tr (\mathbf{\Lambda})= tr (\mathbf{A}^{\prime} \mathbf{\Sigma} \mathbf{A}) = tr (\mathbf{\Sigma} \mathbf{A} \mathbf{A}^{\prime}) = tr (\mathbf{\Sigma}) = \sum_{j=1}^{p}Var(X_{j}), \end{split} (\#eq:ecuacion6) \end{equation}\] pudiéndose comprobar que la suma de las varianzas de las variables originales224 coincide con la suma de las varianzas de las c.p.
Por tanto, la m-ésima c.p. captura un porcentaje de la variabilidad de las variables originales cifrado en \(\frac{\lambda_{m}}{\sum_{m=1}^{p} \lambda_{m}} 100\), siendo \(\frac{\sum_{m=1}^k\lambda_{m}}{\sum_{m=1}^{p} \lambda_{m}} 100\) la proporción capturada por las \(k\) primeras componentes.
32.2.2.2 Componentes principales a partir de variables estandarizadas
A menudo, no solo se centran las variables originales sino que también se estandarizan, para que tengan varianza unitaria.225 La razón es que si las variables originales presentan grandes diferencias en sus escalas de medida o en los rangos de las unidades de medida (edad en años, altura en metros, longitud en kilómetros…), sus combinaciones lineales tendrán poco significado, porque las variables que las conforman no son “igualmente importantes” y en la primera componente tendrá un gran peso la variable original con mayor magnitud (Chatfield & Collins, 1980). Si no fuera el caso, es mejor partir de \(\bf\Sigma\); además, la teoría muestral de las c.p. es mucho más compleja cuando las variables están estandarizadas que cuando no lo están (Morrison, 1976).
El mecanismo de obtención de las c.p. no cambia en absoluto, pero su punto de arranque ya no es \(\boldsymbol{\Sigma}\) sino \(\bf{P}\), la matriz de correlaciones de dichas variables. Los autovectores de \(\bf{P}\) son, en general, distintos a los de \(\boldsymbol{\Sigma}\). Además, la suma de los autovalores, como coincide con la suma de las varianzas de las variables originales, es p, luego el porcentaje de la variación total capturada por la componente m-ésima es \(\frac{\lambda_{m}}{p} 100\), siendo \(\frac{\sum_{m=1}^k\lambda_{m}}{p} 100\) la proporción capturada por las \(k\) primeras componentes.
32.2.2.3 Correlación entre las variables originales y las componentes principales
Considérese la variable original \(X_{j}\) y la c.p. \(Y_{m}=a_{1m}X_{1}+a_{2m}X_{2}+\dotsb+a_{pm}X_{p}=\mathbf{a}_{m}^{\prime}\mathbf{X}\). Dado que \(\mathbf{X}^{\prime} = [X_{1},\dotsb,X_{p}]\), entonces \(X_{j}=\mathbf{e}_{j}^{\prime}\mathbf{X}\), donde \(\mathbf{e}_{j}\) es un vector de ceros excepto un 1 en la j-ésima posición.
Entonces, como \(({\bf \Sigma}-{\lambda_{m}} {\bf I)}{\bf {a}}_m=0\), se tiene que \({\bf\Sigma} {\bf a}_m={\lambda}_m {\bf {a}}_m\) y que:
\[\begin{equation} Cov(X_{j},Y_{m})=Cov(\mathbf{e}_{j}^{\prime}\prime\mathbf{X},\mathbf{a}_{m}^{\prime}\mathbf{X})= \mathbf{e}_{j}^{\prime} \mathbf{\Sigma} \mathbf{a}_{m}= \mathbf{e}_{j}^{\prime} \lambda_{m} \mathbf{a}_{m}= \lambda_{m} a_{jm}, \tag{32.4} \end{equation}\] \[\begin{equation} r_{X_{j},Y_{m}}=\frac{Cov(X_{j},Y_{m})}{\sqrt{Var(X_{j})}\sqrt{Var(Y_{m})}}= \frac{\lambda_{m} a_{jm}}{\sqrt{\sigma_{jj}} \sqrt{\lambda_{m}}}= \frac {\sqrt{\lambda_{m}}a_{jm}}{\sigma_{jj}} \tag{32.5}, \end{equation}\]donde \(\sigma_{jj}\) es el elemento j-ésimo de la diagonal principal de \(\boldsymbol{\Sigma}\).
Si se parte de variables estandarizadas, entonces se tiene que \(r_{Z_{j},Y_{m}}=\sqrt{\lambda_{m}}a_{jm}\), donde ahora \(\lambda_{m}\) es el m-ésimo autovalor de \(\bf{P}\) y \(a_{jm}\) es el elemento j-ésimo de su autovector asociado. Sin embargo, el coeficiente de correlación lineal no varía por el hecho de haber estandarizado las variables originales.
Como se verá posteriormente, estos dos coeficientes, \(r_{X_{j},Y_{m}}\) y \(r_{Z_{j},Y_{m}}\), serán de gran utilidad en la interpretación de las c.p. Además, como \(r_{X_{j},Y_{m}}\) coincide con el coseno del ángulo que forma \(X_{j}\) con \(Y_{m}\) (que es la proyección o coordenada de \(X_{j}\) en el eje de \(Y_{m}\)), resulta de gran ayuda para representar las variables originales en el espacio de las componentes y, por consiguiente, para la interpretación de estas últimas. A mayor coseno, mayor correlación lineal entre \(X_{j}\) e \(Y_{m}\). Matricialmente, y denominando \({\mathbf A}^*\) a la matriz de coeficientes de correlación lineal entre las variables originales estandarizadas y las c.p., se tiene que \({\mathbf A}^{*}= {\bf A} {\bf\Lambda}^{\frac {1}{2}}\). \(\mathbf{A}^*\) (imprescindible en la interpretación de las c.p.) no cambia por el hecho de estandarizar también las c.p.
Los cuadrados de los elementos de \(\bf A^*\) expresan la proporción de varianza de la variable \(X_j\) explicada por la componente \(Y_m\). Por tanto, la suma de los cuadrados de las filas de \(\bf A^*\) será la unidad. Se denomina contribución (individual) de \(X_{j}\) a la componente \(Y_{m}\) a la cantidad \(\frac{r_{X_j,Y_m}^2} {\sum_{j=1}^{p} r_{{X_{j},Y_{m}}}^2}=\frac{cos(X_j,Y_m)}{\sum_{j=1}^{p}{cos(X_j,Y_m)}}\).
Otras dos expresiones interesantes que involucran \(\bf A^*\) son \(\bf A^*\bf A^*{^\prime}=\bf {R}\) y \(\bf A^*{^\prime}\bf A^*=\bf {\Lambda}.\)
32.3 Estimación de las componentes principales
Hasta el momento, se han derivado las c.p. suponiendo conocida la matriz de covarianzas poblacional \(\boldsymbol{\Sigma}\) (o la de correlaciones \(\bf P\)). Sin embargo, este no suele ser el caso en la práctica, por lo que se sustituyen por sus homónimas muestrales \({\bf{S}}=\frac {1}{N}\bf{X}^\prime\bf{X}\) (o \(\bf{R}\)). Nada cambia en el proceso de obtención de las c.p., salvo que el punto de partida es \(\bf{S}\) (o \(\bf{R}\)) y que los valores de los autovalores y autovectores asociados son estimaciones.
En el ejemplo que nos ocupa, la matriz de correlaciones muestrales, \(\bf R\), se muestra en la Fig. 32.1. Puede apreciarse que la correlación entre las variables es notable en la mayoría de los casos, lo que invita a analizar el problema con menos variables e incorrelacionadas, es decir, mediante ACP.
library("CDR")
data("TIC2021")
TIC <- TIC2021
library("corrplot")
corrplot.mixed(cor(TIC))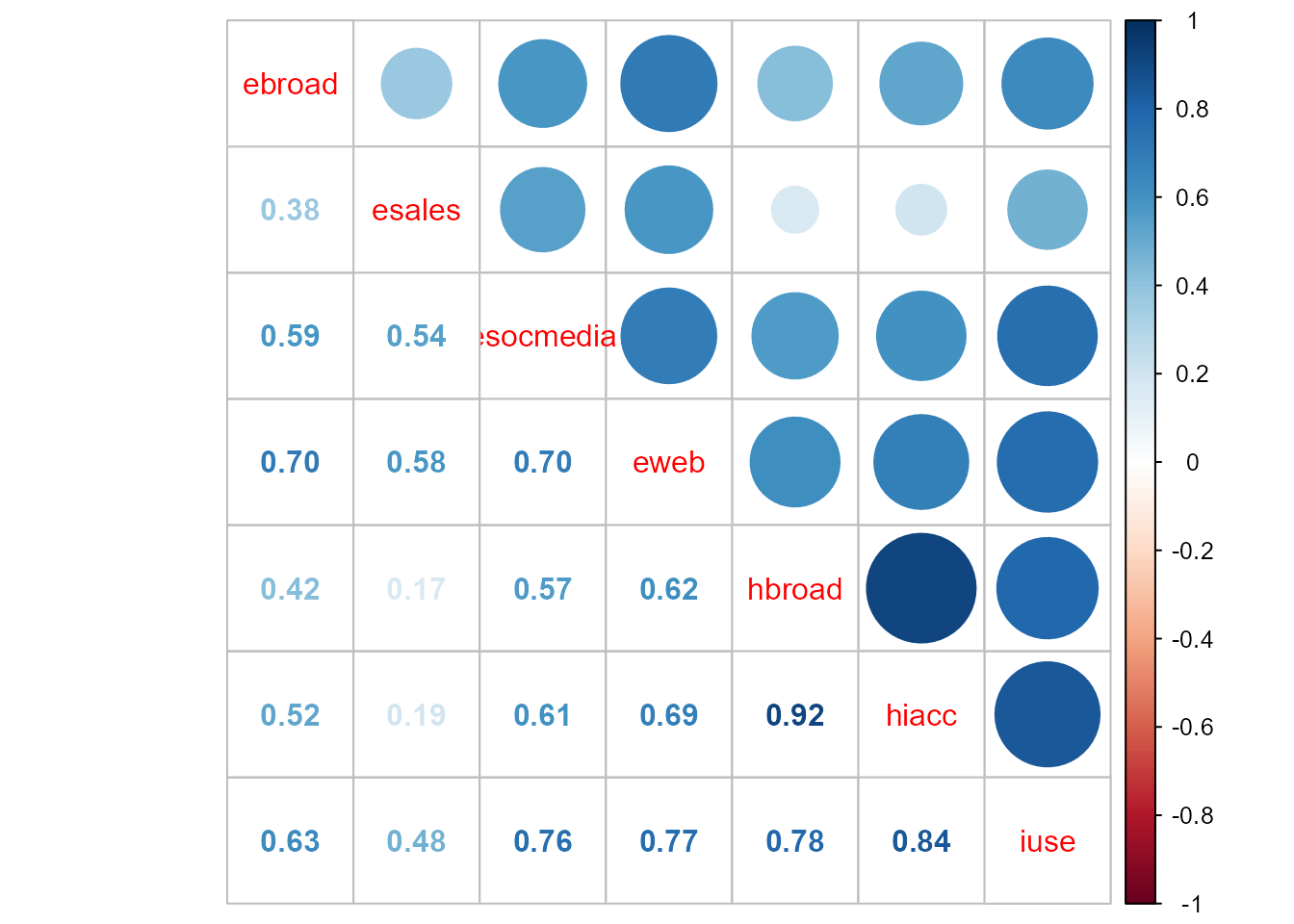
Figura 32.1: Matriz de correlaciones.
library("FactoMineR")
acp<- PCA(TIC, ncp=7, graph=FALSE)32.4 Número de componentes a retener
Dado que la finalidad de la técnica de componentes principales es la reducción de la dimensionalidad, una decisión clave es el número \(k\) de componentes a retener. Los criterios más populares para tomar esta decisión son:
- Seleccionar un número de componentes que capturen, entre todas, un porcentaje de la variabilidad total determinado
Dicho porcentaje suele estar alrededor del 80%, si bien, si el número de c.p. es elevado, su interpretación es muy difícil.
- Criterio de la media aritmética o criterio de Kaiser
Dado que la variabilidad total coincide con la suma de los autovalores, se seleccionan aquellas c.p. cuya varianza exceda la varianza media. Es decir, se selecciona la componente m-ésima si \(\lambda_{m}> \bar{\lambda}\) (si se parte de \(\mathbf\Sigma\)) o si \(\lambda_{m}> 1\) (si se parte de \(\mathbf R\)). En caso de valores anómalos (outliers) es recomendable utilizar la media geométrica en vez de la aritmética.
- Criterio de Catell
Se basa en la representación gráfica de los autovalores vs. su número de orden, que se denomina gráfico de sedimentación porque se asemeja a la ladera de una montaña con su correspondiente zona de sedimentación. Se seleccionan las c.p. asociadas a los autovalores previos a la zona de sedimentación. En general, el criterio de Catell tiende a incluir demasiadas c.p., al contrario que el de la media, que tiende a incluir demasiado pocas (sobre todo si \(p<20\)) (Mardia et al., 1979).
- Otros criterios
Otros criterios menos populares son la validación cruzada, el test de esfericidad o igualdad de autovalores de Anderson (requiere normalidad multivariante) y el criterio del bastón roto (véase Cuadras, 2007 para los dos últimos). Para grandes conjuntos de datos, (jobson1992?) propone un criterio basado en la partición de la muestra en submuestras mutuamente excluyentes, similar a la validación cruzada.
La Fig. 32.2 muestra el gráfico de sedimentación en el ejemplo que nos ocupa. Puede apreciarse que con tan solo las dos primeras c.p. se captura el 82,07% de la variabilidad total de las siete variables originales.
round(acp$eig[1:7,1:2], 3)
#> eigenvalue percentage of variance
#> comp 1 4.644 66.341
#> comp 2 1.101 15.731
#> comp 3 0.547 7.814
#> comp 4 0.328 4.679
#> comp 5 0.191 2.731
#> comp 6 0.124 1.768
#> comp 7 0.066 0.937
library("factoextra")
fviz_eig(acp, addlables=TRUE)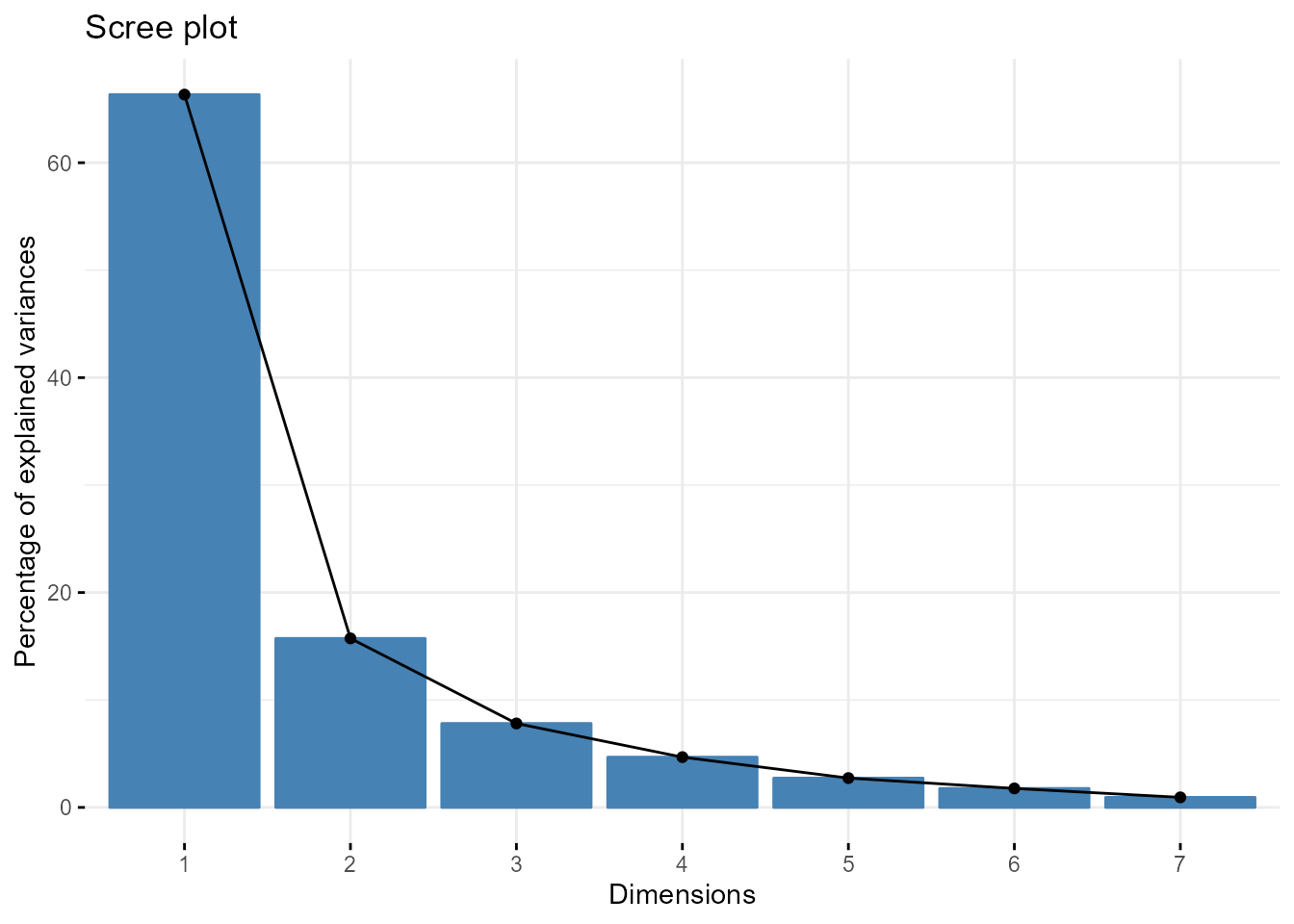
Figura 32.2: Gráfico de sedimentación.
32.5 Interpretación de las componentes principales
Una primera vía consiste en analizar el signo y la magnitud de los coeficientes (cargas o loadings) de cada variable original en cada componente.
loadings<- sweep(acp$var$coord,2,sqrt(acp$eig[1:7,1]))
round(loadings,3)
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7
#> ebroad -1.410 -0.854 -1.358 -0.561 -0.303 -0.271 -0.259
#> esales -1.604 -0.318 -0.411 -0.404 -0.310 -0.262 -0.225
#> esocmedia -1.317 -0.858 -0.645 -1.062 -0.536 -0.311 -0.244
#> eweb -1.264 -0.865 -0.825 -0.356 -0.773 -0.422 -0.284
#> hbroad -1.343 -1.550 -0.570 -0.495 -0.413 -0.159 -0.386
#> hiacc -1.290 -1.496 -0.675 -0.495 -0.413 -0.348 -0.053
#> iuse -1.217 -1.135 -0.652 -0.587 -0.255 -0.608 -0.331- Una segunda vía es el análisis de los \(r_{X_{j},Y_{m}}, \hspace{0,2cm} \forall {j,m=1,...,p}\).
round(acp$var$cor,3)
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7
#> ebroad 0.745 0.195 -0.618 0.012 0.134 0.081 -0.003
#> esales 0.551 0.731 0.328 0.169 0.128 0.090 0.031
#> esocmedia 0.838 0.191 0.095 -0.490 -0.099 0.040 0.012
#> eweb 0.891 0.185 -0.085 0.217 -0.336 -0.070 -0.028
#> hbroad 0.812 -0.501 0.170 0.077 0.024 0.193 -0.129
#> hiacc 0.865 -0.446 0.065 0.077 0.024 0.003 0.203
#> iuse 0.938 -0.086 0.087 -0.014 0.183 -0.256 -0.075
fviz_pca_var(acp,
col.var = "contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)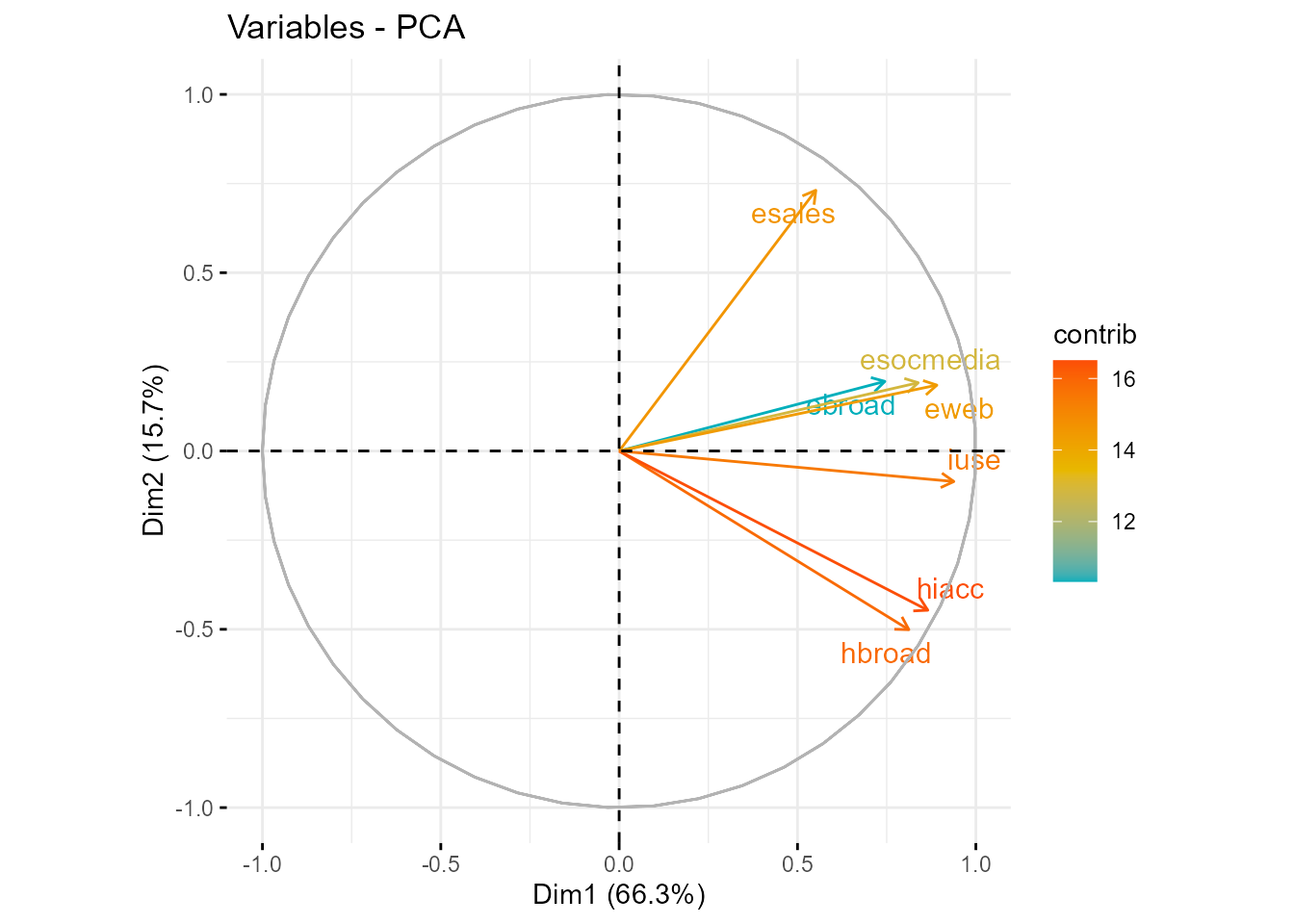
Figura 32.3: Gráfico de cosenos o coeficientes de correlación variables-componentes.
Se puede utilizar cualquiera de las dos vías, pues los resultados no serán contradictorios (véase Fig. 32.3). Sin embargo, algunos autores recomiendan no utilizar solo la segunda, pues los \(r_{X_{j},Y_{m}}\) tienen en cuenta únicamente la variable original considerada y no el resto; es decir, se estarían interpretando las componentes desde una perspectiva univariante.
Nota
También es de interés la siguiente consideración: cuando las variables originales están correlacionadas positivamente, la primera c.p. tiene todas sus coordenadas del mismo signo y puede interpretarse como un promedio ponderado de todas ellas.
En la matriz de cargas (o loadings) se aprecia que la primera c.p. es una media ponderada (con ponderaciones similares) de las variables originales, mientras que esales, hbroad y hiacc cargan fuertemente en la segunda (esales positivamente y las otras dos de forma negativa) (Fig. 32.4). La interpretación desde la perspectiva univariante de los coeficientes de correlación lineal es prácticamente la misma. Por ello, cabe interpretar la primera c.p. como un indicador general del uso de las TIC, mientras que la segunda, positivamente relacionada con la dotación TIC de las empresas pero con una fuerte relación negativa con la de los individuos y hogares, pudiera estar relacionada con las ayudas públicas a la implantación de las TIC en el tejido empresarial.
acp1<- fviz_contrib(acp, choice = "var", axes=1, top = 10)
acp2<- fviz_contrib(acp, choice = "var", axes=2, top = 10)
library(patchwork)
acp1 + acp2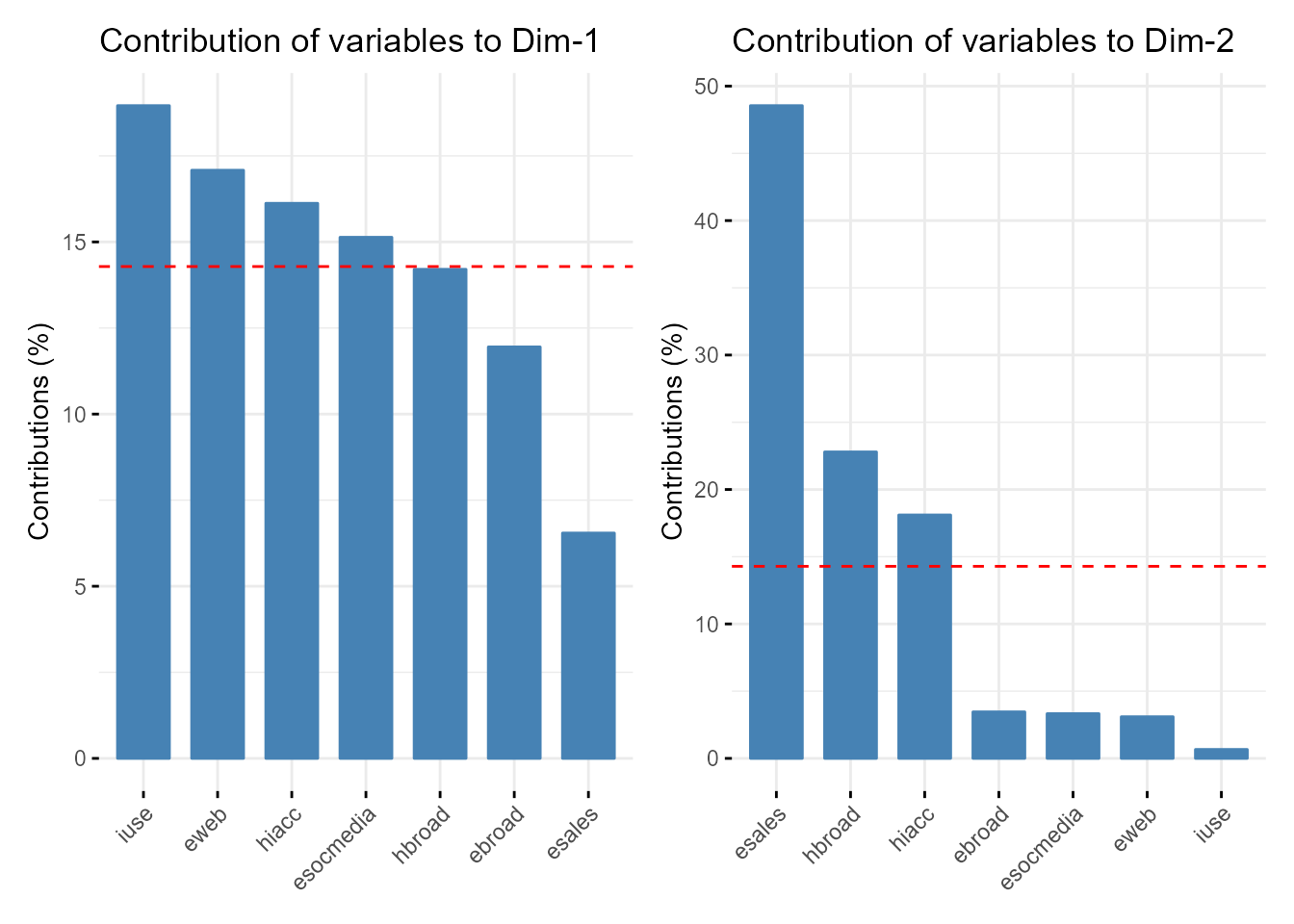
Figura 32.4: Contribución de las variables originales a las componentes retenidas.
32.6 Reproducción de los datos tipificados y de \(\bf R\) a partir de las componentes principales
En la práctica, el punto de partida del ACP es la matriz \(\bf R\), y en tal caso se suelen estandarizar también las c.p. Pues bien, se tiene que:
\[\begin{equation} \tag{32.6} {\bf Y^*}= {\bf X A} {\bf \Lambda}^{-\frac {1}{2}}= \bf X\bf A \bf{\Lambda^{\frac {1}{2}}} \bf\Lambda^{-1}=\bf X\bf A^*\bf\Lambda^{-1}=\bf X\bf F, \end{equation}\]
donde \(\bf F\) es la matriz de puntuaciones de las c.p. La expresión anterior proporciona las coordenadas de los \(N\) elementos en el espacio de las c.p. y, por tanto, sirve de ayuda en la interpretación de estas. La estandarización de las c.p. asegura que los \(m\) ejes (componentes) tengan una métrica homogénea que facilitará la visualización e interpretación. Dichas coordenadas también constituyen el input de técnicas híbridas como, por ejemplo, regresión con c.p., clúster o PLS.
En el ejemplo del uso de las TIC se tiene que:
puntuaciones<- acp$ind$coord
round(puntuaciones[1:5,],3)
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7
#> BE 1.651 1.053 0.310 -0.238 -0.196 0.296 -0.196
#> BG -4.759 -0.127 -0.128 -0.223 0.023 -0.013 -0.106
#> CZ -0.324 0.875 -0.564 0.870 -0.082 -0.032 -0.345
#> DK 3.188 1.331 0.497 0.262 0.343 -0.300 0.319
#> DE 0.024 0.144 -0.183 0.560 -0.871 -0.485 0.115De la expresión (32.6) se deduce que \({\bf X}={\bf Y} {\bf \Lambda}^{-\frac{1}{2}} {\bf\Lambda}^{\frac{1}{2}}{\bf A}^\prime={\bf Y^*}_{N \times k}{\bf A^*}^\prime_{k \times p}\), expresión que permite reproducir la matriz \(\bf X\) a partir de las \(k\) primeras c.p. estandarizadas. En consecuencia, la reproducción de \(\bf R\) a partir de las \(k\) primeras c.p. estandarizadas se lleva a cabo como sigue: \[\begin{eqnarray} {\bf R}_{p \times p} = \frac {1}{N} {\bf X}^{\prime}_{p \times N} {\bf X}_{N \times p}= {\bf A}^{*}_{p \times k} \frac {1} {N} {\bf Y}^{*^{\prime}}_{k \times N} {\bf Y}^{*}_{N \times k} {\bf A}^{*^{\prime}}_{k \times p} \nonumber\\ ={\bf A}^{*}_{p \times k} {\bf I}_{k\times k}{\bf A}^{*^{\prime}}_{k \times p}={\bf A}^{*}_{p \times k}{\bf A}^{*^{\prime}}_{k \times p}. \end{eqnarray}\] Debajo se muestran las tres primeras filas de la reproducción de \(\bf R\) a partir de las dos primeras c.p. De la comparación de sus valores con los de la verdadera \(\bf R\) (Fig. 32.1) se concluye que se trata de una buena reproducción.226
32.7 Limitaciones del análisis de componentes principales
Una primera limitación es que su implementación solo es posible si todas las variables se trabajan bajo un nivel de análisis numérico. Otra limitación importante es el supuesto subyacente de que los datos observados son combinación lineal de una cierta base. Es decir, solo se consideran las combinaciones lineales de las variables originales. Otros métodos de reducción de la dimensionalidad como, por ejemplo, el t-distributed stochastic neighbor embedding (\(t\)SNE), o la versión Kernel de la técnica, que también funcionan con no linealidad, superan esta limitación.
Además, el hecho que todas las c.p. sean combinaciones lineales de todas las variables originales dificulta su interpretación. Para superar esta limitación han surgido algunas alternativas, como el sparse PCA, que obtiene las c.p. como un problema minimización del error de reconstrucción forzando a que los autovectores tengan una gran parte de sus componentes nula.
El \(t\)-SNE no es la única alternativa no lineal procedente de la comunidad de machine learning. Otras, denominadas actualmente “aprendizaje múltiple” (manifold learning), incluyen el Sammon’s mapping, el curvilinear component analysis (CCA) y sus variantes: los Laplacian eigenmaps y el maximum variance unfolding (MVU); véase Wismüller et al. (2010).
Finalmente, cabe señalar que el ACP es una técnica matemática que no requiere que las variables originales sigan una distribución normal multivariante, aunque, si así fuera, se podría dar una interpretación más profunda de las c.p.
Resumen
El ACP es una técnica de reducción de la dimensionalidad que captura un gran porcentaje de la variabilidad de un conjunto de variables correlacionadas a partir de un número mucho menor de componentes latentes (las componentes principales) incorrelacionadas.
La piedra angular de la construcción de estas componentes son los autovalores de la matriz de covarianzas (o de correlaciones) de las variables originales.
En el ACP son cuestiones importantes, entre otras: \((i)\) la determinación del número de componentes a retener, \((ii)\) su interpretación y \((iii)\) la cuantificación del valor de las componentes para cada observación (puntuaciones), que constituyen el input de técnicas híbridas como, por ejemplo, regresión con componentes principales, clúster o partial least squares.