Capítulo 17 Modelos aditivos generalizados

María Durbán$^{a}$ y Víctor Casero-Alonso$^{b}$

$^{a}$Universidad Carlos III de Madrid
$^{b}$Universidad de Castilla-La Mancha

17.1 Introducción

Los modelos lineales, o los lineales generalizados (GLM), vistos en los capítulos 15 y 16 tienen la ventaja de ser fáciles de ajustar e interpretar. Además, se dispone de técnicas para contrastar las hipótesis del modelo. Sin embargo, cuando la variable respuesta no está relacionada de forma lineal con las variables explicativas no tiene sentido utilizar modelos lineales (generalizados o no) y hay que acudir a modelos que flexibilicen esta relación, que, en el caso de una única variable explicativa, se puede expresar como sigue: \[Y=\beta_0+f(X)+\varepsilon.\]

Puede que la función $f()$ sea conocida de antemano, como ocurre en muchos modelos biológicos, donde existe una dependencia de tipo exponencial, $f(x)=e^{\beta_0+\beta_1x}.$ En otras ocasiones, dicha función es desconocida y se puede utilizar una aproximación. Por ejemplo, mediante la regresión polinómica, muy utilizada en la práctica: \[\begin{equation} Y = \beta_0 + \beta_1 X + \beta_2 X^2 + \ldots + \beta_p X^p + \varepsilon, \quad \varepsilon \sim N(0,\sigma^2). \tag{17.1} \end{equation}\]

Sin embargo, la regresión polinómica tiene un gran inconveniente: que no se lleva a cabo de forma local y, por tanto, cada vez que se cambia un coeficiente del modelo, el cambio impacta a los valores ajustados en todo el rango de la variable explicativa. No obstante, es posible utilizar técnicas (como las que se presentan en este capítulo) en las que el valor predicho en un punto dado solo depende de las observaciones en ese punto y de las observaciones vecinas, es decir, el ajuste se lleva a cabo de forma local.

En el caso de disponer de más de una variable explicativa, la extensión del modelo de regresión múltiple sería el modelo aditivo (en el caso de variable respuesta gaussiana), donde no se asume que la relación entre la variable respuesta y cada una de las variables explicativas tenga que ser lineal:

\[\begin{equation} Y= f(X_{1})+\ldots +f(X_p)+\epsilon, \quad \varepsilon \sim N(0,\sigma^2). \tag{17.2} \end{equation}\]

Las funciones $f()$ incluyen también a las funciones lineales vistas en el Cap. 15. Los modelos aditivos generalizados, GAM, extienden el modelo anterior a respuestas no gaussianas, como lo hacen los GLM respecto de los modelos lineales con respuesta gaussiana (véase Cap. 16).

17.2 Splines con penalizaciones

Las funciones de la ecuación (17.2) se estiman mediante técnicas de suavizado o smoothers, cuyo objetivo es extraer las tendencias (o señales) existentes en la relación entre la variable respuesta y las variables explicativas, sin presuponer una forma funcional a priori para ellas; solo se asume que la relación entre $Y$ y $X$ es suave (tiene poco ruido). Las predicciones obtenidas mediante estas técnicas tienen menos variabilidad que la variable respuesta; de ahí que a estas técnicas se les denomine suavizadores (la regresión lineal es un suavizador llevado al extremo). Las siguientes son algunas de las técnicas de suavizado más populares:

Regresión polinomial local con pesos, lowess.
Kernels.
Splines.

Este capítulo se centra en uso de los splines, ya que es la técnica de suavizado más utilizada. Los splines son funciones polinómicas a trozos de la variable explicativa, que se unen en puntos llamados nodos. Existen muchos tipos de splines (naturales, cíclicos, B–splines, O–splines, etc.). Independientemente del tipo de spline, este capítulo se centra en los splines con penalizaciones (P–splines), que se basan en: $(i)$ hacer una aproximación de la función $f()$ mediante una base de funciones, y $(ii)$ añadir una penalización a la hora de estimar el modelo, de manera que se pueda controlar la variabilidad de la curva que se quiere estimar. Hay muchas maneras de representar una función a través de una base de funciones (un ejemplo sencillo de una base de funciones es el caso de la regresión polinómica, en la que la base de funciones, es decir, la matriz de regresión, es una matriz cuyas columnas son las potencias de la variable explicativa: $[X:X^2:\ldots : X^p]$). Una de las mejores opciones son los B–splines (De Boor, 2001), debido a sus buenas propiedades numéricas. La penalización se añade en la función de verosimilitud y se construye a partir de la derivada de la curva que se quiere penalizar. Generalmente se utilizan penalizaciones de orden 2, lo que implica que se penaliza todo aquello que no es lineal en la función; por tanto, si la penalización es muy grande la curva estimada es simplemente una línea recta. La penalización está controlada por un parámetro llamado parámetro de suavizado (Eilers et al., 2015 para más detalle; véanse Eilers & Marx, 2010).

A la hora de ajustar este tipo de modelos hay que tomar dos decisiones importantes:

El número de nodos del B–spline: generalmente se utiliza esta regla: \[\begin{equation} \text{número de nodos}=min\{40,\text{valores únicos de }X/4\} \tag{17.3} \end{equation}\] (por ejemplo, si se tienen 100 observaciones diferentes, se elegirían $100/4=25$ nodos).
El valor del parámetro de suavizado: se puede estimar por distintos métodos: validación cruzada, validación cruzada generalizada, máxima verosimilitud, máxima verosimilitud restringida, etc. Se recomienda reexpresar el modelo como un modelo mixto (véase Cap. 18) y estimarlo mediante el método de máxima verosilimitud restringida, REML,¹⁴² para así poder estimar el parámetro de suavizado junto con los demás parámetros del modelo.

La Fig. 17.1 muestra el impacto que el parámetro de suavizado tiene en el ajuste final de la curva (los datos corresponden al dataset fossil del paquete Semipar).

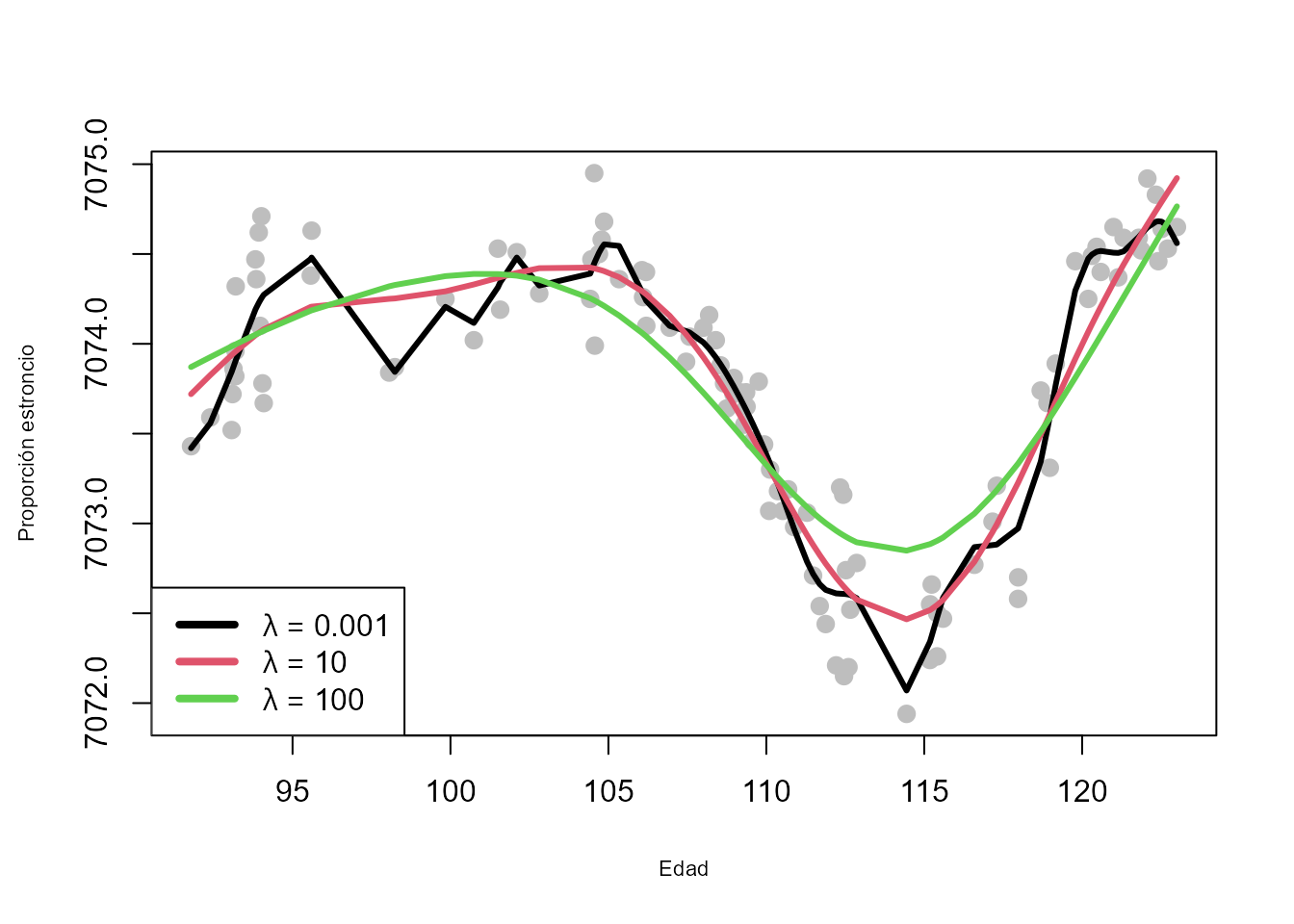
Figura 17.1: Regresión con $P$-$splines$ para diferentes valores del parámetro de suavizado.

17.3 Aspectos metodológicos

Al igual que en el caso de los modelos lineales y los modelos GLM, en los modelos GAM es necesario conocer algunos aspectos metodológicos que son fundamentales para llevar a cabo un ajuste correcto de los modelos y entender los resultados obtenidos en el ajuste. A continuación se muestran los más relevantes.

17.3.1 Estimación de los parámetros del modelo

La estimación de los modelos GAM se lleva a cabo mediante máxima verosimilitud penalizada. Supóngase el caso de una sola variable explicativa y que se quiere ajustar el modelo: \[Y= f(X)+\epsilon.\] Como se comentó anteriormente, los modelos GAM tienen como punto de partida la aproximación de la función a estimar mediante una matriz formada por B–splines; es decir, se busca transformar el modelo lineal o lineal generalizado tradicional de tal forma que $f(X)$ sea el producto de una matriz multiplicada por unos coeficientes (esa matriz está formada por los B–splines). En otros términos, se elige una base (una matriz $\textbf{B}$) que permita escribir la función $f(X)$ como una combinación lineal de sus elementos (los elementos de esta base son conocidos ya que se calculan a partir de las variables explicativas): \[f(X)=\sum_{l=1}^k b_l(X)\theta_l,\] donde $b_l(X)$ son las funciones B–spline que componen la base. En forma matricial: \[f(X)=\textbf{B}\boldsymbol{\theta}.\] Los parámetros $\boldsymbol{\theta}$ se estiman minimizando la siguiente expresión (en el caso de asumir gaussianidad para los errores, y por tanto para la variable respuesta, los mínimos cuadrados penalizados son equivalentes a la máxima verosimilitud penalizada):

\[(\bf{y}-\bf{B}\boldsymbol{\theta})^\prime(\bf{y}-\bf{B}\boldsymbol{\theta}) + \lambda\boldsymbol{\theta}^\prime\bf{P}\boldsymbol {\theta},\] donde $\boldsymbol{P}$ es la matriz de penalización y $\lambda$ es el parámetro de suavizado. Dado un valor del parámetro de suavizado, las estimaciones de los parámetros vienen dadas por:¹⁴³

\[\begin{equation} \hat{\boldsymbol{\theta}} = (\bf{B}^{\prime}T \bf{B} +\lambda \bf{P} )^{-1}\bf{B}^\prime\bf{y}, \tag{17.4} \end{equation}\]

y las estimaciones de la variable respuesta se obtienen como: $\hat{ \bf{y}}= \underbrace{\bf{B}(\bf{B}^\prime\bf{B} +\lambda \bf{P} )^{-1}\bf{B}^\prime}_{\bf{H}}\bf{y}$. La matriz $\bf{H}$ juega un papel importante, ya que la suma de su diagonal da una idea de la complejidad de la curva ajustada (la curva más compleja sería la que interpola los datos). Dicha suma se denomina grados de libertad efectivos (que no se corresponden con el número de parámetros ajustados).

17.3.2 Inferencia sobre las funciones suaves

Para saber si la relación estimada entre $Y$ y $X$ es o no estadísticamente significativa, se debe proceder al contraste: \[\begin{eqnarray*} H_0: f(X)=0 & \text{ (no efecto)}\\ H_1: f(X)\neq 0 & \text{ (efecto)}. \end{eqnarray*}\]

Dado que la función $f(X)$ depende de los coeficientes que acompañan a las bases de B–splines, el contraste anterior es equivalente al contraste: \[\begin{eqnarray*} H_0: &&\boldsymbol{\theta}=0 \\ H_1: && \boldsymbol{\theta}\neq 0. \end{eqnarray*}\] La distribución del estadístico de contraste dependerá de si la variable respuesta sigue una distribución normal o no: en caso afirmativo el estadístico de contraste sigue un distribución $F$. En caso negativo, sigue una distribución $\chi^2$.

Comparación de modelos

Cuando se trabaja con un modelo aditivo (17.2) en el que hay más de una variable explicativa, puede ser de interés comparar versiones de ese modelo que contengan distintos conjuntos de variables. La comparación dependerá de la relación entre los modelos a comparar:

Modelos anidados. La comparación se basa, igual que en los GLM, en la diferencia en la deviance residual. Si se quieren comparar dos modelos $m_1$ y $m_2$ (donde $m_1\subset m_2$), entonces:

En el caso de variable respuesta normal, el estadístico de contraste es: \[\frac{(DR(m_1)-DR(m_2))/(df_2-df_1)}{DR(m_2)/(n-df_2)}\approx F_{(df_2-df_1), (n-df_2)},\]

donde $DR$ es la deviance residual (suma de cuadrados residual) y $df$ son los grados de libertad asociados con cada modelo.

En otro caso, se utiliza como estadístico de contraste el siguiente:

\[DR(m_1)-DR(m_2)\approx \chi^2_{df_2-df_1}.\]

Modelos no anidados. En este caso los contrastes anteriores no son válidos y se utilizarán criterios basados en el AIC (criterio de información de Akaike).

17.3.3 Suavizado mutidimensional y para datos no gaussianos

Para el suavizado penalizado en 2 dimensiones (o más) también se necesita una base y una penalización. El modelo sería: \[{Y} = \beta_0+ f\left({X}_{1},{X}_{2}\right)+{\epsilon},\] donde $f()$ es una función de las dos covariables ${X}_{1}$ y ${X}_{2}$. Dicha función se aproxima mediante el producto tensorial de las bases de B–splines marginales para cada una de las covariables y la penalización dependerá de dos parámetros de suavizado. Los términos de suavizado multidimensional se pueden combinar con términos unidimensionales y términos lineales. En este caso, la penalización dependería de dos parámetros de suavizado (uno para cada covariable).

La extensión de los modelos de suavizado al caso en el que la variable respuesta no sea gaussiana, se hace de forma similar al caso lineal, cuando se pasa de un modelo de regresión lineal a un GLM. Al igual que en el caso de los GLM, $g({\boldsymbol\mu})=\boldsymbol{\eta}=f(\bf{X})=\bf{B} \boldsymbol{\theta}$, y se añade la penalización a la función de verosimilitud de la distribución correspondiente: \[\ell_p(\boldsymbol{\theta})=\ell(\boldsymbol{\theta})+\lambda \boldsymbol{\theta}^\prime \bf P \boldsymbol{\theta},\] donde $\ell(\boldsymbol{\theta)}$ es la log-verosimilitud.

17.4 Procedimiento con R: la función `gam()` del paquete `mgcv`

Aunque hay muchas librerías disponibles, la principal es mgcv, que implementa una gran variedad de modelos de suavizado a través de la función gam() (generalized additive models).¹⁴⁴

gam(formula, method = "", select = "", family = gaussian())

formula es el argumento principal de esta función; es la ecuación del modelo: por ejemplo, y ~ x1 + x2 + s(x3).
- Lo primero que se tiene que elegir es la base a utilizar para representar las funciones suaves, s(x) (véase ?s o ?smooth.terms), o te(x1,x2) en el caso de suavizado bidimensional. Por defecto se usan los llamados thin plate splines. El tipo de base usada se puede modificar utilizando el argumento bs dentro de s(x, bs = "ps"); en este caso ps indica el uso de B–splines con penalizaciones. A continuación se describen otras alternativas:

`bs`	Descripción
`tp`	Thin plate regression splines
`ts`	Thin plate regression splines con regularización
`cr`	Splines cúbicos de regresión
`crs`	Splines cúbicos de regresión con regularización
`cc`	Splines cíclicos
`ps`	P–splines

m indica el orden de la penalización; por defecto es 2.
k es el número de nodos para construir la base. El número por defecto suele ser demasiado bajo, por lo que siempre se recomienda que el usuario elija el número utilizando la regla dada en (17.3).
by debe igualarse a una variable numérica o factor de la misma dimensión de cada covariable, para hacer interacciones entre curvas y variables.
id se utiliza para forzar que diferentes términos suaves utilicen la misma base y la misma cantidad de suavizado.
method selecciona el método para estimar el parámetro de suavizado. Se puede elegir entre: REML (máxima verosimilitud restringida), ML (máxima verosimilitud), GCV.Cp (validación cruzada generalizada), GACV.Cp (validación cruzada aproximada generalizada). En la práctica, como se indicó anteriormente, se prefiere REML.
family permite elegir la distribución de la variable respuesta (binomial, Poisson, etc.); por defecto asume gaussiana.
select = TRUE contrasta si una variable debe entrar o no en el modelo.

Es importante reseñar que si el método elegido para estimar el parámetro de suavizado es REML, entonces, internamente, el modelo se transforma en un modelo mixto y lo estima junto con el resto de los parámetros del modelo (véase Cap. 18).

17.5 Casos prácticos

En este apartado se ven una serie de aplicaciones que permiten mostrar los diferentes usos de este tipo de modelos.

17.5.1 Modelo unidimensional con `fossil`

Se empieza ilustrando el uso de la función gam() con el conjunto de datos fossil del paquete SemiPar. El objetivo es estimar la relación entre la edad de los fósiles y la proporción de isótopos de estroncio.

library("SemiPar")
data(fossil)
Y <- 10000 * fossil$strontium.ratio
X <- fossil$age
plot(X, Y, xlab = "Edad", ylab = "Proporción de estroncio")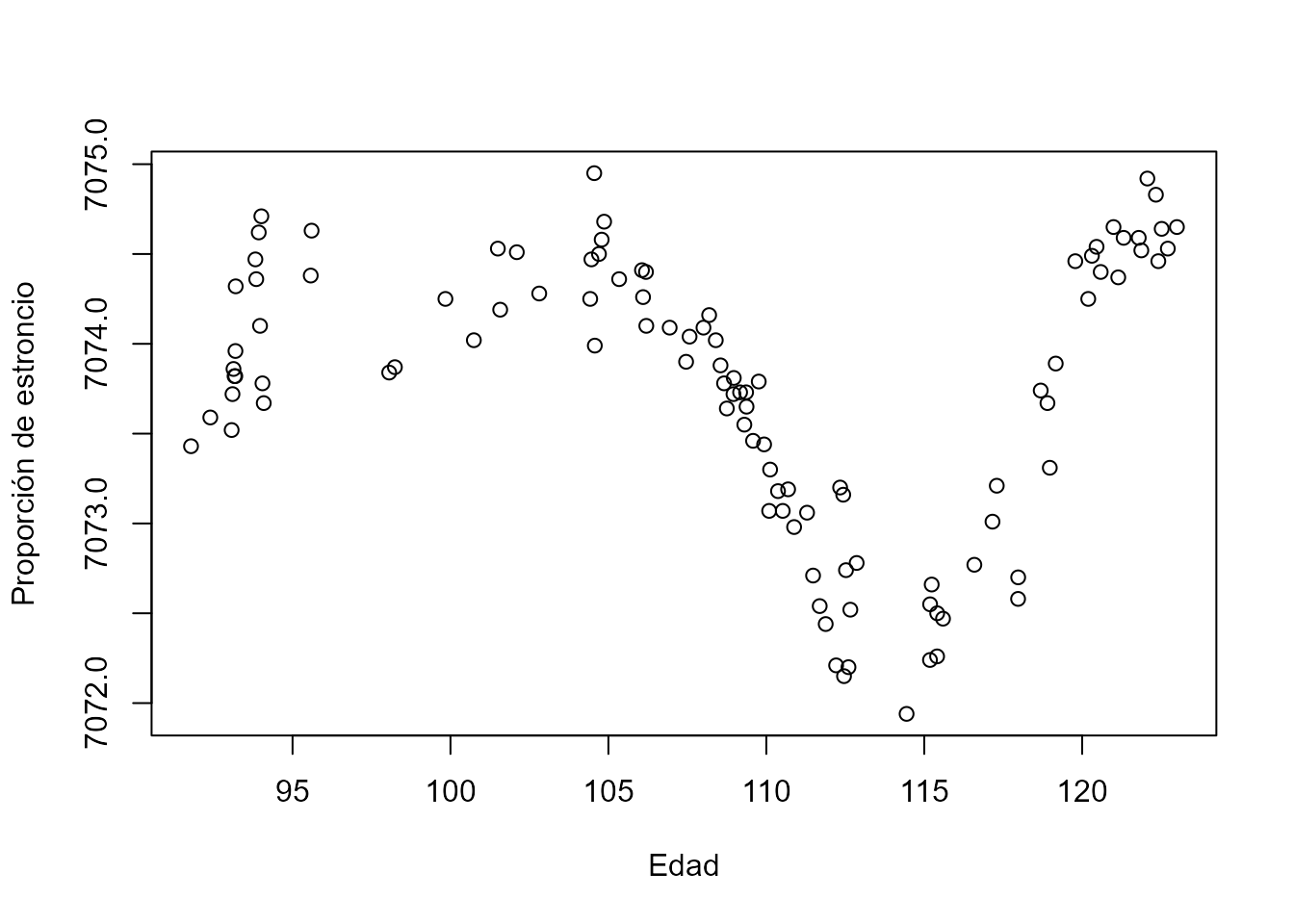

Figura 17.2: Edad de los fósiles con respecto a la proporción de isótopos de estroncio.

A la vista de la Fig. 17.2, está claro que se necesita ajustar una curva (y no una línea) para estimar la relación entre ambas variables. Para ello se utiliza la función gam(), que devuelve un objeto de tipo "gam" y que se puede usar con las típicas funciones print(), summary(), fitted(), plot(), residuals(), etc.

library("mgcv")
fit_gam <- gam(Y ~ s(X, k = 25, bs = "ps"), method = "REML", select = TRUE)
# se eligen 25 nodos ya que se lavariable tiene 106 observaciones
summary(fit_gam)
#> 
#> Family: gaussian 
#> Link function: identity 
#> 
#> Formula:
#> Y ~ s(X, k = 25, bs = "ps")
#> 
#> Parametric coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 7.074e+03  2.435e-02  290504   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Approximate significance of smooth terms:
#>        edf Ref.df     F p-value    
#> s(X) 10.22     24 35.89  <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> R-sq.(adj) =  0.891   Deviance explained = 90.2%
#> -REML = 23.946  Scale est. = 0.062849  n = 106

Como se puede ver, la relación entre la variable respuesta (Y, proporción de estroncio) y la variable explicativa ($X$, edad) se ha especificado mediante un spline, s(), de tipo penalizado, ps, con 25 nodos. Se ha seleccionado REML como método para estimar el parámetro de suavizado (los parámetros del spline se estiman también mediante REML, ya que da lugar a las mismas estimaciones que máxima verosimilitud).

En la primera parte de la salida anterior aparecen los términos que entran linealmente en el modelo (en este caso solo el término independiente o intercepto); en la parte de abajo se muestran los términos de suavizado. Como se indicó anteriormente, dado que se ha usado select=TRUE, se está contrastando si la variable edad debe entrar en el modelo o no. En este caso, es claro que ha de entrar ya que el p–valor de s(x) es pequeño y los grados de libertad asociados son aproximadamente 10, lo que indica que la relación entre $Y$ y $X$ está lejos de la linealidad.

La función gam.check() devuelve los gráficos de residuos usuales (residuos frente a valores ajustados, gráficos de cuantiles para comprobar la normalidad, etc., Fig. 17.3), pero, además, proporciona información sobre el proceso de ajuste del modelo.

gam.check(fit_gam, cex = 1.2)
#>
#> Method: REML Optimizer: outer newton
#> full convergence after 5 iterations.
#> Gradient range [-4.557319e-06,5.900149e-06]
#> (score 23.94602 & scale 0.06284944).
#> Hessian positive definite, eigenvalue range [4.557347e-06,53.03185].
#> Model rank = 25 / 25
#>
#> Basis dimension (k) checking results. Low p-value (k-index<1) may
#> indicate that k is too low, especially if edf is close to k'.
#>
#> k' edf k-index p-value
#> s(X) 24.0 10.2 1.03 0.63

knitr::include_graphics("img/gam_check.png")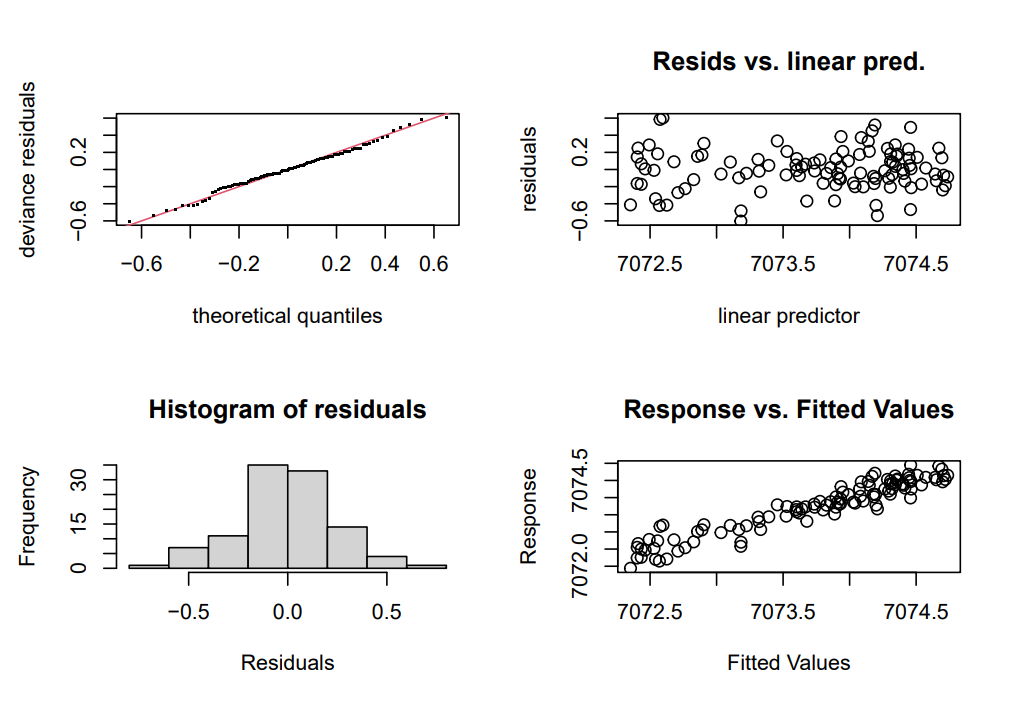

Figura 17.3: Gráficos de residuos obtenidos con $gam.check().$

El test que aparece en la parte de abajo está contrastando si el número de nodos elegido es suficiente. Si el valor de k está muy próximo al de edf, entonces se debería reajustar el modelo con más nodos.

El comando plot() permite dibujar la función suave que relaciona $Y$ con $X$. La curva estimada que aparece en la Fig. 17.4 está centrada (la función plot() siempre lo hace de esta forma), el argumento shade hace que se sombree el intervalo de confianza y seWithMean hace que la incertidumbre sobre el término independiente se incluya en el cálculo del intervalo de confianza.

plot(fit_gam, shade = TRUE, seWithMean = TRUE, pch = 19, 1, cex = .55)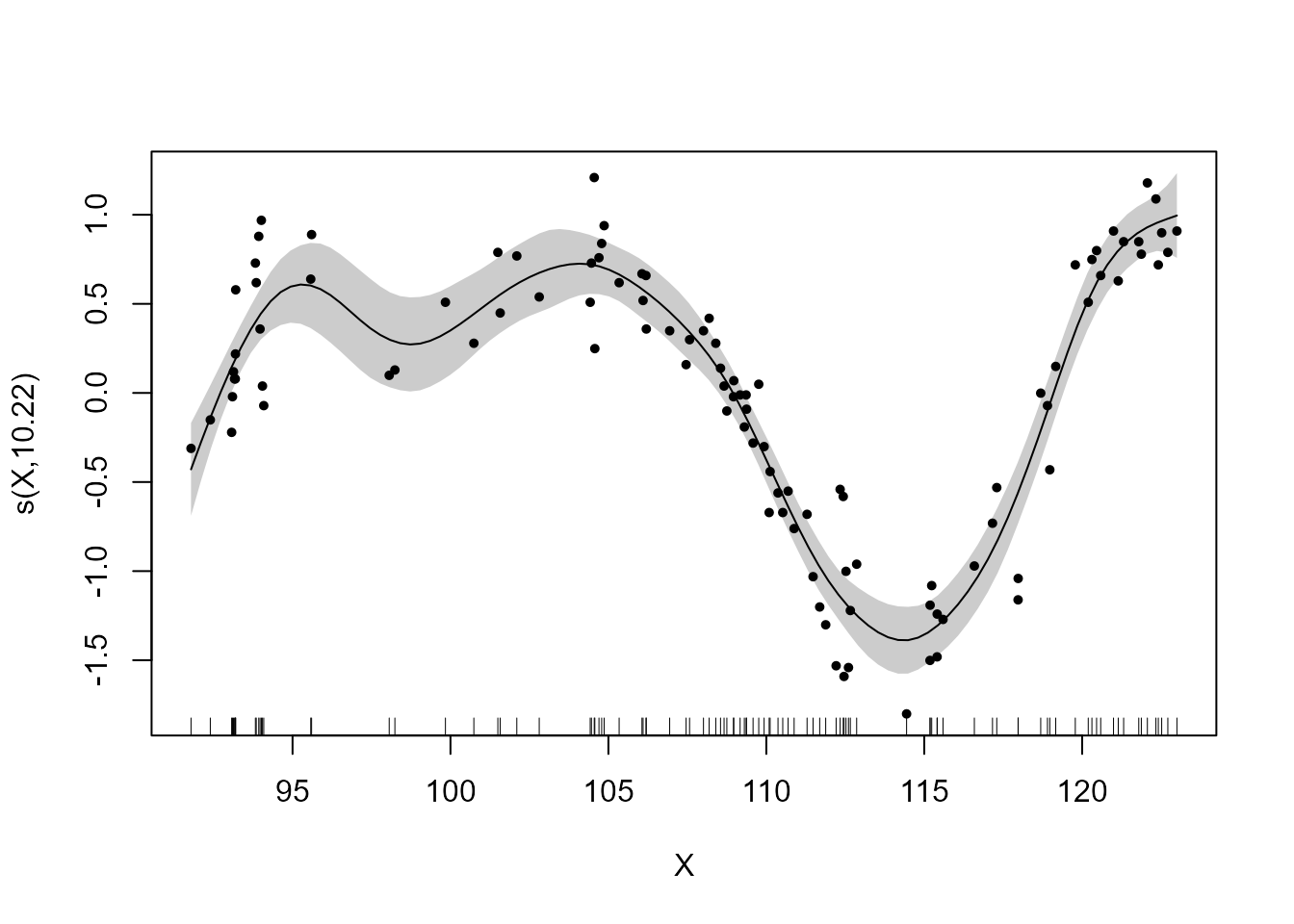

Figura 17.4: Curva ajustada e intervalo de confianza.

17.5.2 Modelo aditivo con `airquality`

En esta sección se analizan de nuevo los datos airquality (ver airquality¹⁴⁵), que consisten en 154 medidas de calidad del aire en Nueva York, de mayo a septiembre de 1973. El objetivo es establecer la relación entre las variables meteorológicas y el nivel de concentración de ozono en la atmósfera. Ya se ha analizado dicha relación en el Cap. 15, donde los ajustes lineales realizados eran satisfactorios pero se encontraban problemas en los residuos del modelo, lo cual impedía validar la modelización realizada. Allí se sugería que la relación entre la variable respuesta y alguna explicativa fuese no lineal. Además, se consideró la transformación logarítmica de la variable Ozone, y con dicha trasformación se obtenía una distribución más similar a la distribución normal.

En consecuencia, se va a ajustar el modelo incluyendo las variables explicativas sin imponerles linealidad; en particular, se van a incluir las variables Wind, Temp y Solar.R. Las variables Wind y Temp tienen solo 31 y 40 valores únicos, respectivamente, aunque el conjunto de datos tiene 154 valores; por eso, para estas dos variables, se decide establecer el número de nodos en 10 y no más; para la variable Solar.R el número de nodos se fija en 20.


airq_gam <- gam(
  log(Ozone) ~ s(Wind, bs = "ps", k = 10) +
    s(Temp, bs = "ps", k = 10) + s(Solar.R, bs = "ps", k = 20),
  method = "REML", select = TRUE, data = airquality, na.action = na.omit
)
summary(airq_gam)
#> 
#> Family: gaussian 
#> Link function: identity 
#> 
#> Formula:
#> log(Ozone) ~ s(Wind, bs = "ps", k = 10) + s(Temp, bs = "ps", 
#>     k = 10) + s(Solar.R, bs = "ps", k = 20)
#> 
#> Parametric coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  3.41593    0.04586   74.49   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Approximate significance of smooth terms:
#>              edf Ref.df     F  p-value    
#> s(Wind)    2.318      9 2.255 3.13e-05 ***
#> s(Temp)    1.852      9 6.128  < 2e-16 ***
#> s(Solar.R) 2.145     19 1.397 2.31e-06 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> R-sq.(adj) =  0.689   Deviance explained = 70.7%
#> -REML = 86.106  Scale est. = 0.23342   n = 111

Los resultados indican que todas las variables son significativas (p–valores pequeños), estando la variable Temp próxima a la linealidad (los grados de libertad efectivos asociados a la variable son 1,8). El $R^2$ ajustado es 0,69, por lo que el modelo ajusta moderadamente bien los datos.

La Fig. 17.5 muestra las tres curvas ajustadas junto con sus correspondientes intervalos de confianza. También incluye los denominados residuos parciales que corresponden a, por ejemplo, en el caso del gráfico del viento, $log(Ozone)-\hat \beta_0-\hat f(Temp)- \hat f(Solar.R)$, es decir, lo que queda sin explicar después de haber ajustado los demás términos del modelo.

library("mgcViz")
# getViz es otra opción para dibujar los términos de un modelo gam()
b <- getViz(airq_gam)
pl <- plot(b) + l_points() + l_fitLine(linetype = 2) + l_ciLine(colour = 2)
print(pl, pages = 1)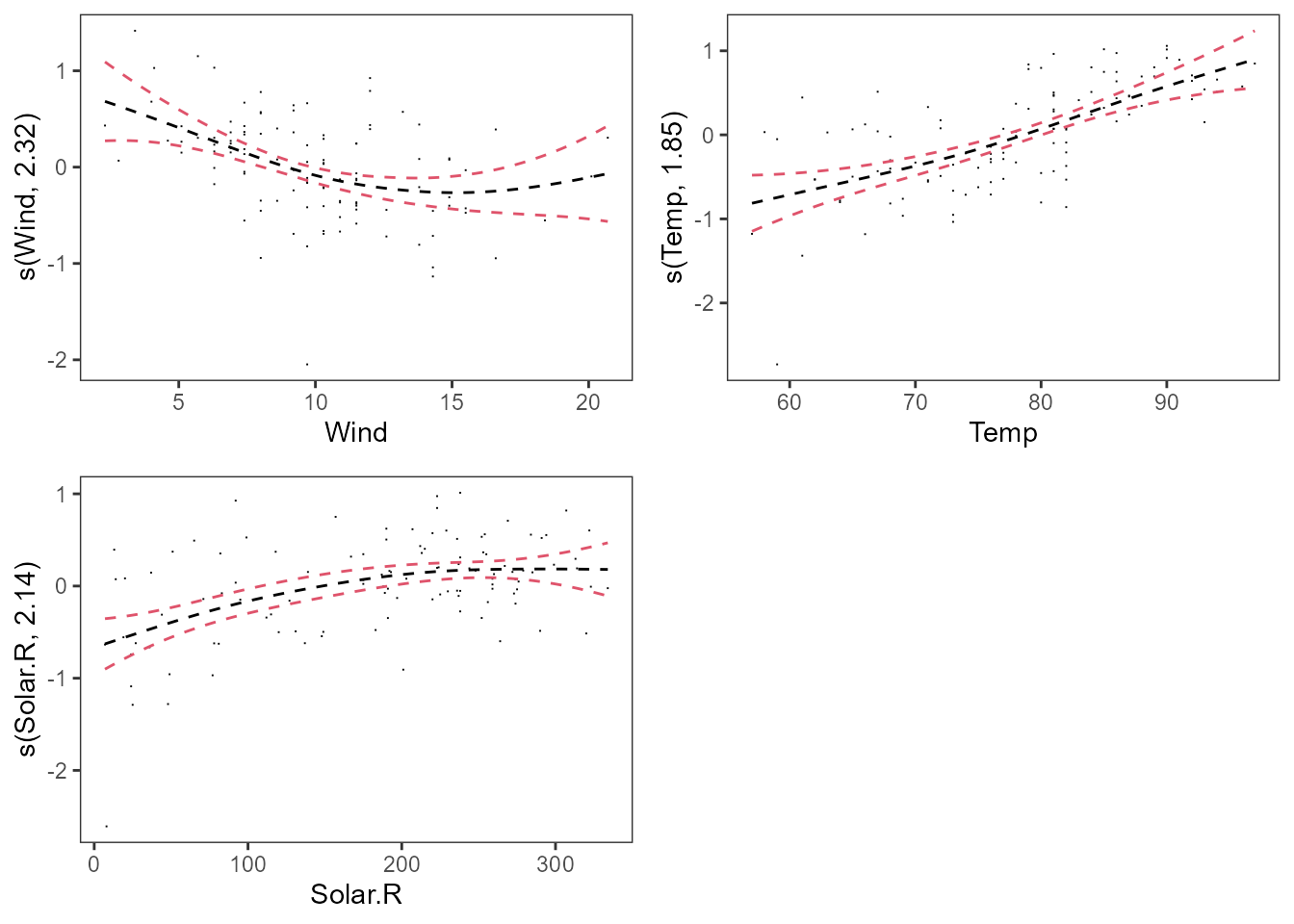

Figura 17.5: Curvas estimadas para $Wind$, $Temp$ y $Solar$.

17.5.3 Modelo semiparamétrico con `onions`

Es un caso particular del modelo aditivo, pues en este modelo todas las variables entran de forma lineal excepto una: \[{Y}= \beta_0 +\beta_1 {X}_{1}+\ldots + \beta_{p-1}{X}_{p-1}+f({X}_p)+\epsilon.\]

La forma de ajustar el modelo es exactamente igual a la anterior. Pero hay un caso que merece especial interés: cuando en la parte paramétrica se incluye una variable categórica con dos o más niveles. Al igual que en el caso de regresión lineal, se puede plantear si se quieren ajustar dos o más rectas paralelas (modelo aditivo) o no paralelas (modelo con interacción).

Para ilustrar este caso se acude al data.frame onions (librería SemiPar). Contiene 84 observaciones de un experimento sobre la producción de un tipo de cebolla en dos localidades: Purnong Landing (la localidad de referencia) y Virginia. El objetivo es relacionar el logaritmo de la producción de cebollas con la densidad de plantas por metro cuadrado, dens. El modelo lineal básico sería: \[ \log(\text{yield}_i) = \beta_0 + \beta_1\text{location}_{i} + \beta_2 \text{dens}_i + \epsilon_i,\] donde \[\text{location}_{i} = \left\{\begin{array}{cl} 0 & \mbox{si la observación $i$ es de Purnong Landing.} \\ 1 & \mbox{si la observación $i$ es de Virginia.} \end{array}\right.\]

Se comienza por ajustar el siguiente modelo: \[ \log(\text{yield}_i) = \beta_0 + \beta_1\text{location}_{i} + f(\text{dens}_i) + \epsilon_i.\]

library("mgcv")
library("SemiPar")
data(onions)
# Se indica a R que la variable locationVirginia es categórica
onions$location <- factor(onions$location)
# Se recodifica la variable
levels(onions$location) <- c("Purnong Landing", "Virginia")
fit1 <- gam(log(yield) ~ location + s(dens, k = 20, bs = "ps"),
  method = "REML", select = TRUE, data = onions
)
summary(fit1)
#> 
#> Family: gaussian 
#> Link function: identity 
#> 
#> Formula:
#> log(yield) ~ location + s(dens, k = 20, bs = "ps")
#> 
#> Parametric coefficients:
#>                  Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)       4.85011    0.01688  287.39   <2e-16 ***
#> locationVirginia -0.33284    0.02409  -13.82   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Approximate significance of smooth terms:
#>           edf Ref.df     F p-value    
#> s(dens) 4.568     19 72.76  <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> R-sq.(adj) =  0.946   Deviance explained = 94.9%
#> -REML = -54.242  Scale est. = 0.011737  n = 84

En este ejemplo se ve que en la parte lineal aparecen dos parámetros, ambos significativos: la ordenada en el origen o intercepto y el coeficiente de la categoría Virginia de la variable location, que es negativo, indicando que la producción media en Purnong Landing es mayor que en Virginia. El término de suavizado también es significativo.

En este caso, la función plot.gam() solo dibuja una curva, pues las curvas para las dos localizaciones son paralelas y la diferencia entre ellas es igual al valor del parámetro correspondiente a localización. Para dibujar las curvas para cada localización se utiliza la función plot_smooth() de la librería tidymv. Los argumentos son: primero el modelo, después la variable explicativa y, por último, la variable categórica (Fig. 17.6).

library("tidymv")
library("ggplot2")
plot_smooths(fit1, dens, location) +
  theme(text = element_text(size = 12))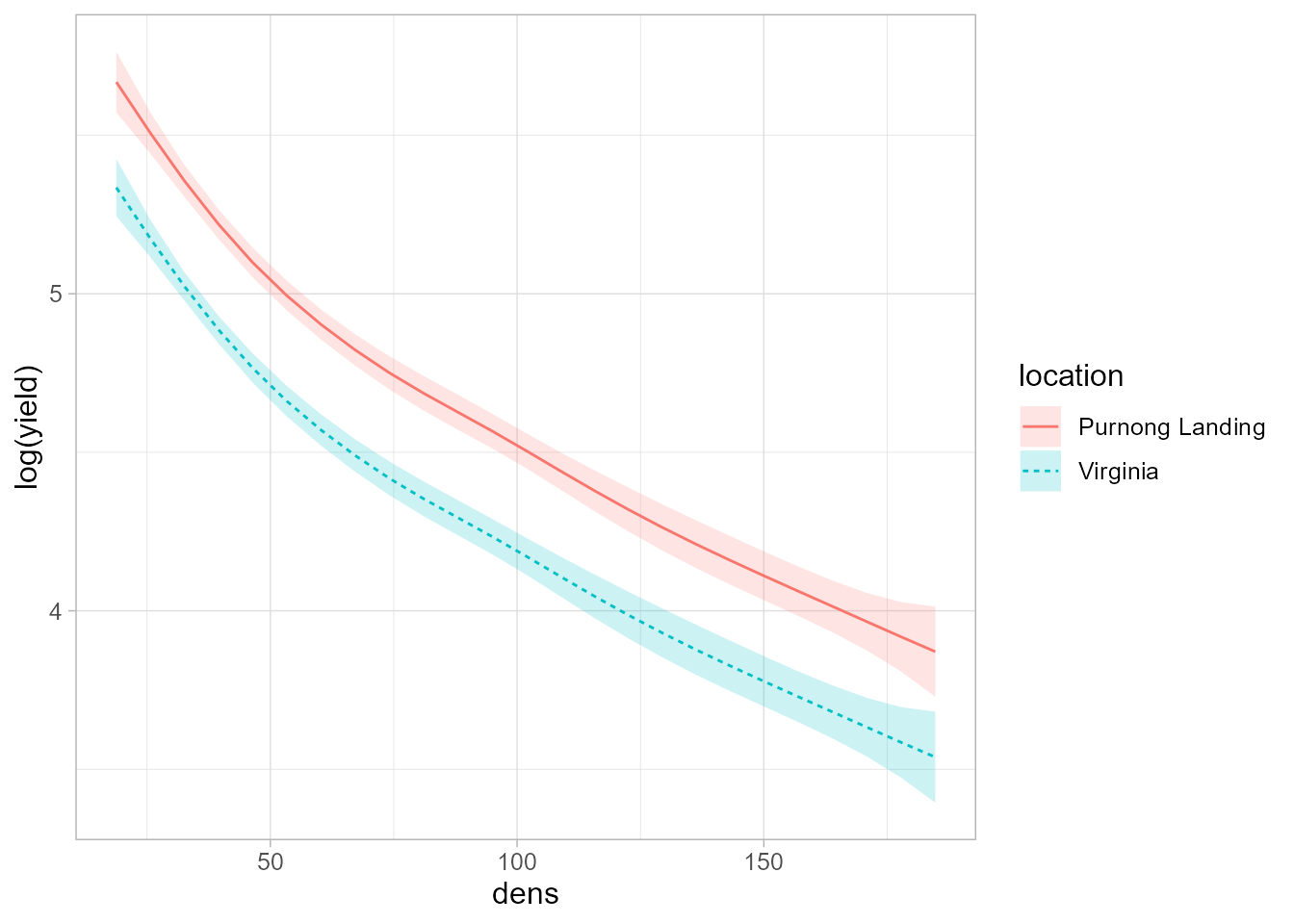

Figura 17.6: Curvas ajustadas para ambas localidades.

Asumir curvas paralelas para ambas localidades implica que el descenso en la producción de cebollas a medida que aumenta la densidad de plantas es el mismo para ambas localidades, y esto no tiene por qué ser cierto. Para relajar esta hipótesis se puede ajustar un modelo con interacción (de manera similar a lo que se hace en el caso de regresión lineal): \[\log(\text{yield}_i) =\beta_0 + \beta_1\text{location}_{i} + f(\text{dens}_i){L(i)} + \epsilon_i,\] donde \[L(i) = \left\{\begin{array}{cl} 0 & \mbox{si la $i$-ésima observación es de Purnong Landing.} \\ 1 & \mbox{si la $i$-ésima observación es de Virginia.} \end{array}\right.\]

Para hacerlo en R, se introduce el argumento by=location dentro de la curva (Fig. 17.7).

fit2 <- gam(log(yield) ~ location + s(dens, k = 20, bs = "ps", by = location),
  method = "REML", data = onions
)
summary(fit2)
#> 
#> Family: gaussian 
#> Link function: identity 
#> 
#> Formula:
#> log(yield) ~ location + s(dens, k = 20, bs = "ps", by = location)
#> 
#> Parametric coefficients:
#>                  Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)       4.84415    0.01603  302.19   <2e-16 ***
#> locationVirginia -0.33018    0.02270  -14.54   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Approximate significance of smooth terms:
#>                                   edf Ref.df     F p-value    
#> s(dens):locationPurnong Landing 3.096  3.834 176.9  <2e-16 ***
#> s(dens):locationVirginia        4.742  5.795 153.0  <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> R-sq.(adj) =  0.952   Deviance explained = 95.7%
#> -REML = -58.541  Scale est. = 0.010446  n = 84

Ahora aparecen dos términos suaves, uno para cada localidad, de modo que estas curvas no tienen por qué ser paralelas, sino que cada una se ajustará a la forma que tengan los datos. En este caso, la Fig. 17.7, generada de nuevo con plot_smooths, muestra como las curvas se van alejando a medida que aumenta la densidad de plantas.

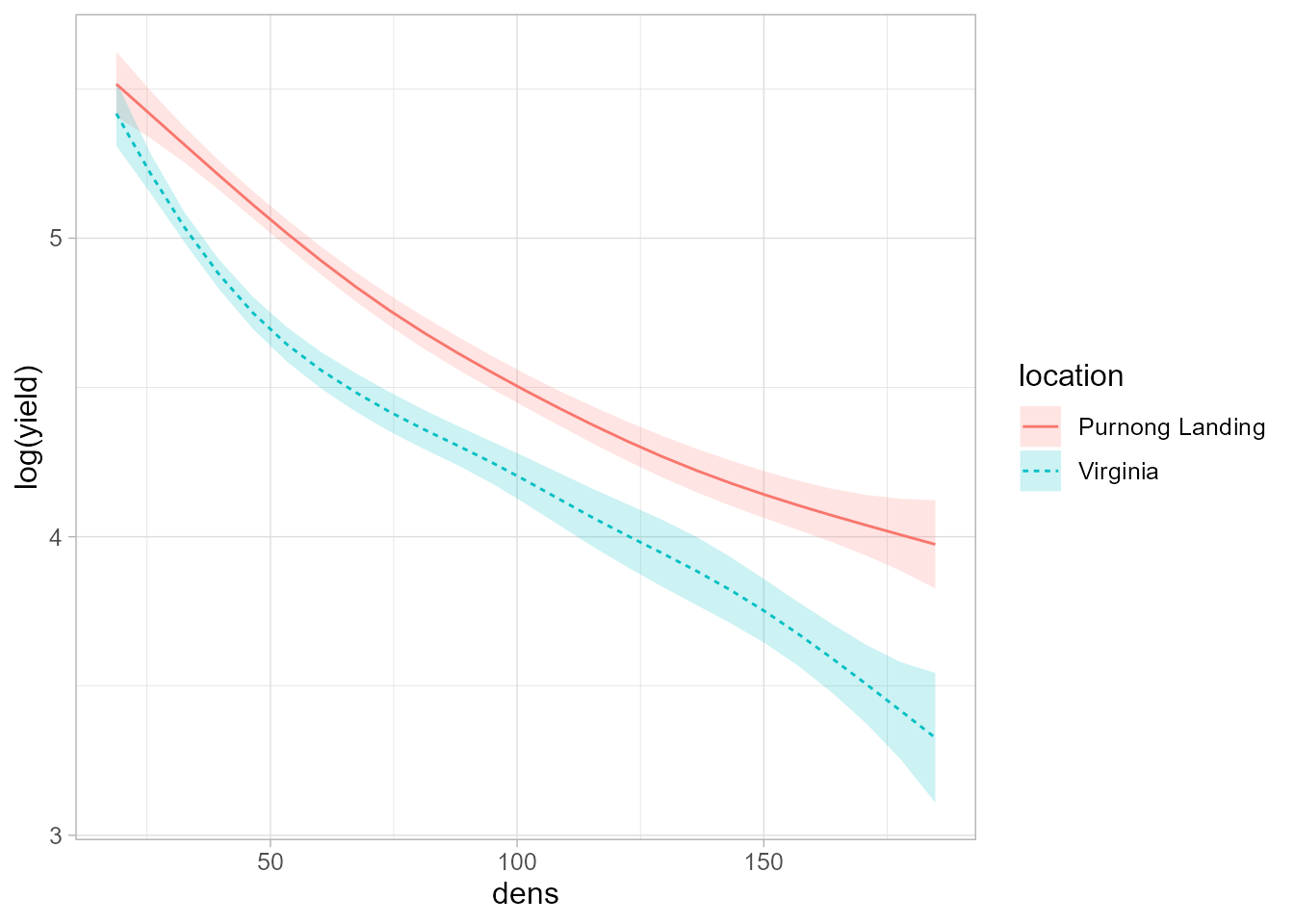
Figura 17.7: Curvas ajustadas para ambas localidades permitiendo que no sean paralelas.

Para finalizar se comparan ambos modelos con el criterio AIC.

AIC(fit1)
#> [1] -125.2307
AIC(fit2)
#> [1] -131.2181

Dado que el menor valor se alcanza en el segundo modelo, se escogería el modelo que incluye la interacción entre la variable densidad y la localidad.

17.5.4 Modelo aditivo generalizado y multidimensional con `smacker`

En este epígrafe se analizan los datos smacker del paquete sm. El objetivo es ver cómo influyen las condiciones del mar (temperatura de agua, etc.) en la ausencia o presencia de huevos de jurel en el mar Cantábrico. Además, se incorporará al modelo la posición geográfica mediante las covariables latitud y longitud; de esta forma se podrá captar el efecto espacial.

library("sm")
data(smacker)
library("dplyr")
smacker <- smacker |>
  mutate(
    Presence = ifelse(Density > 0, 1, 0),
    smack.long = -smack.long,
    ldepth = log(smack.depth)
  )
library("maps")
par(pty = "s")
Position <- cbind(smacker$smack.long, smacker$smack.lat)
plot(Position, col = NULL, xlim = c(-10, -1), ylim = c(43, 48), cex = 1.2, xlab = "longitud", ylab = "latitud")
map("world", add = TRUE, fill = TRUE, col = "grey")
points(Position[smacker$Presence == 1, ], pch = 1, cex = .5, col = 4)
points(Position[smacker$Presence == 0, ], pch = 16, cex = .5, col = 2)
legend("topleft", c("Presencia ", "Ausencia"), col = c(4, 2), pch = c(1, 16), cex = .85)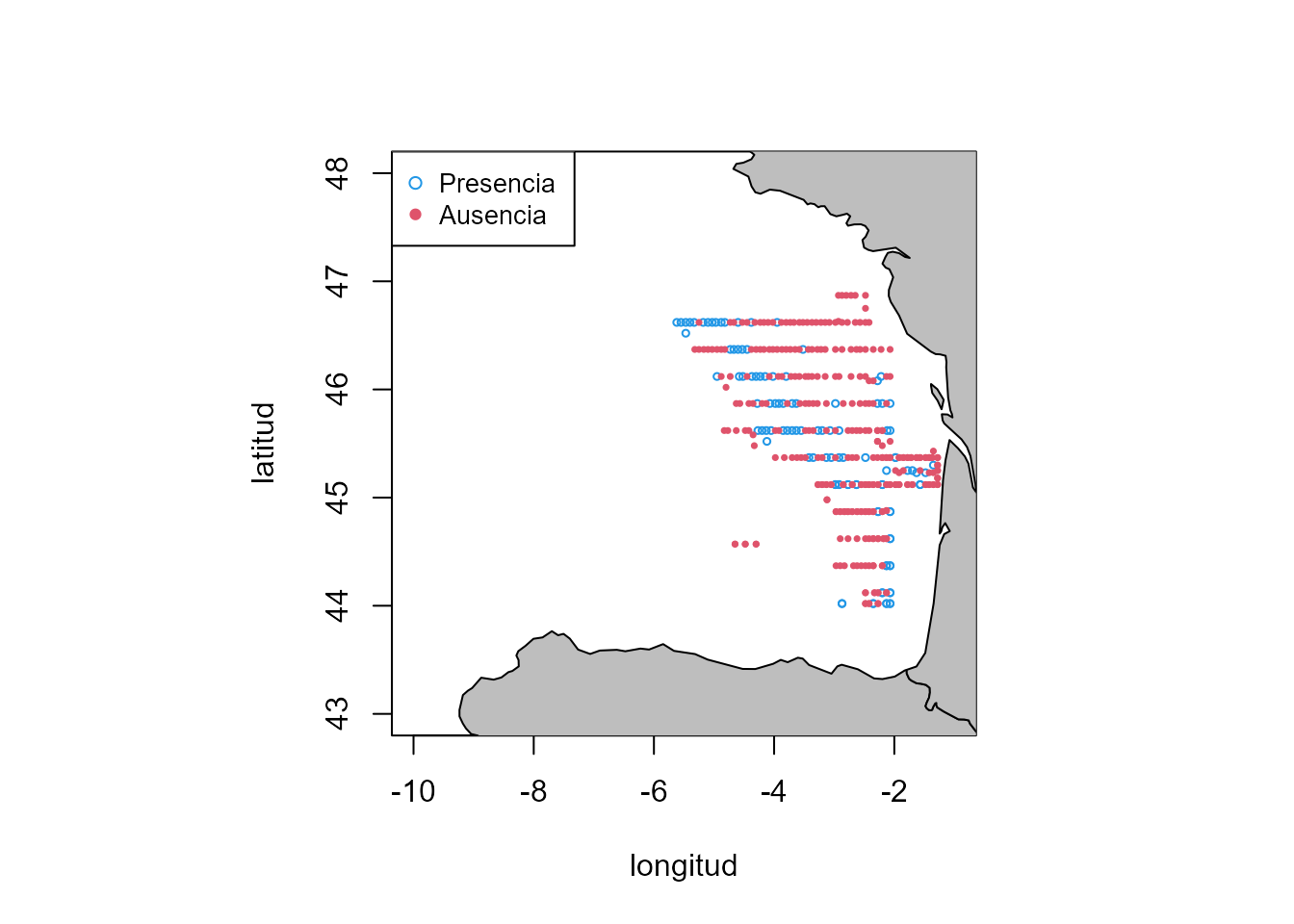

Figura 17.8: Área donde se constató la ausencia/presencia de huevos de jurel.

Dado que la variable respuesta es dicotómica, se utiliza un modelo de regresión logística en el que se flexibiliza la relación lineal de las variables explicativas con la respuesta y, además, se usa una superficie para estimar el efecto de la localización como una función en dos dimensiones (latitud y longitud, Fig. 17.8). En este caso, en vez de usar te() se usa s() también para el caso de 2 dimensiones. La diferencia fundamental con te() es que s() asume un suavizado isotrópico, es decir, el mismo parámetro de suavizado para la latitud y longitud. No se debe usar s() para el suavizado en dos dimensiones si las covariables están medidas en unidades diferentes. En este caso, como tanto la longitud como la latitud están medidas en las mismas unidades, se puede usar el suavizado isotrópico.

logit1 <- gam(Presence ~ s(ldepth) + s(Temperature) + s(smack.long, smack.lat, k = 60),
  family = binomial, select = TRUE, data = smacker
)
b <- getViz(logit1)
print(plot(b, allTerms = T), pages = 1)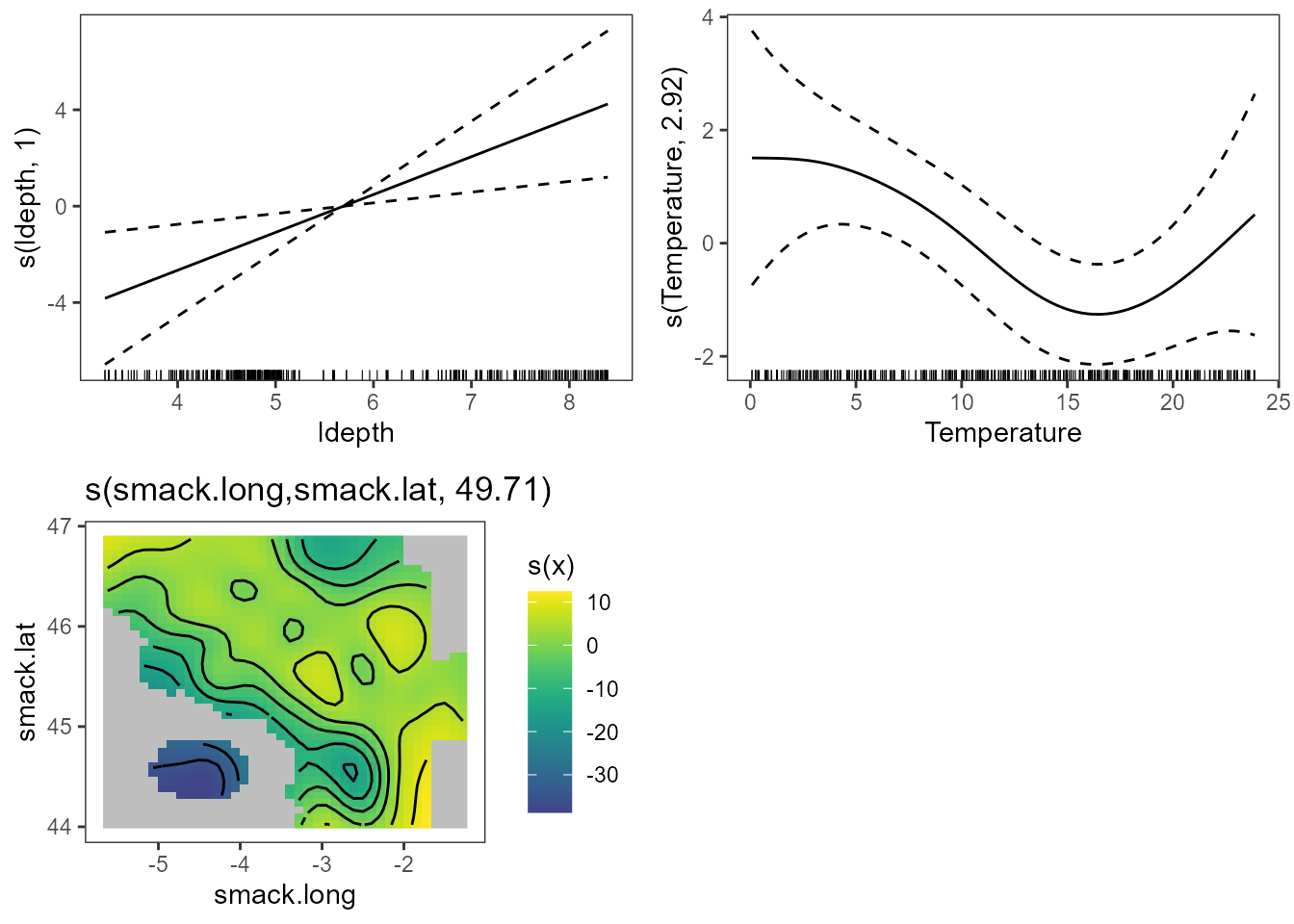

Efectos suaves estimados por el modelo para las variables. Efecto de la profundidad y temperatura en la fila superior y efecto espacial en la inferior.

Figura 17.9: Efectos suaves estimados por el modelo para las variables. Efecto de la profundidad y temperatura en la fila superior y efecto espacial en la inferior.

En la Fig. 17.9 se aprecia que la relación entre la probabilidad de presencia de huevos y la temperatura no es lineal, mientras que sí lo es en el caso de la profundidad. El $R^2$ es tan solo $0,4$, por lo que convendría utilizar más variables explicativas para obtener buenas predicciones.

Las probabilidades predichas se pueden obtener con la función predict.

prob <- predict(logit1, type = "response")

Resumen

En este capítulo se introducen los modelos aditivos generalizados. En particular:

Se presentan distintos aspectos metodológicos de carácter inferencial en este tipo de modelos.
Se muestra el uso de R para llevar a cabo su ajuste.
Se presentan diversos casos prácticos que ilustran la versatilidad de estos modelos para analizar datos complejos.

16 Modelos lineales generalizados

18 Modelos mixtos