Capítulo 60 Detección de fraude de tarjetas de crédito
Pedro Albarracín García
DXC Technology
60.1 Introducción
En un informe publicado en diciembre de 2021 por Nilson Report,311 se anunció que los emisores de tarjetas de crédito, comerciantes y consumidores sufrieron un total de 28.580 millones de dólares de pérdidas por fraude en 2020, es decir, 6,8 centavos por cada 100 dólares en volumen de compras. Solo el fraude representa el 35,83% del total mundial.
En Europa la situación no es más alentadora. Según un informe del Banco Central Europeo publicado en 2020,312 el valor total de las transacciones con tarjeta en la zona SEPA ascendió a 4,84 billones de euros en 2018, de los cuales 1.800 millones correspondieron a operaciones fraudulentas.
Las entidades financieras trabajan a diario en el desarrollo de modelos de machine learning y deep learning que les permitan detectar, con la mayor precisión posible, aquellas operaciones de compra con tarjetas de crédito, débito o prepago que puedan ser sospechosas de fraude, o que al menos puedan ser identificadas como anómalas. En este sentido, es importante destacar que no existe una única solución posible, ya que el problema presenta, en la mayoría de los casos, múltiples variantes que hacen de este un problema complejo y que puede y debe ser abordado desde múltiples perspectivas y con diferentes enfoques.
En primer lugar, es posible identificar dos tipos de fraude. Por un lado, el que se comete físicamente, como, por ejemplo, la compra o la retirada de efectivo con tarjetas robadas o falsas. Por otro lado, están aquellas transacciones fraudulentas que se cometen online, en las que no es necesaria la tarjeta física, y en las que se utilizan los datos de las tarjetas obtenidas por los delincuentes mediante técnicas como el phishing y que son utilizados posteriormente para realizar pagos online.
Otro hándicap asociado a este tipo de escenarios es el derivado de la gran diversidad de fuentes de datos que forman parte de una transacción y que pueden dar lugar a divergencias metodológicas, tanto en la recogida y transmisión de los datos como en su posterior almacenaje, lo que ocasiona que, en muchos casos, la calidad de los datos disponibles no sea la esperada, o simplemente que los datasets sean inconsistentes. Los datos requeridos para este caso de uso pueden categorizarse en variables relativas a:
Cliente.
Transacción.
Geolocalización.
Comercio.
Tarjetas.
Hábitos de compra.
Cada una de estas categorías, y otras que puedan aparecer, aportan información que permite abordar el problema desde diferentes ángulos. Se puede enfocar el problema desde el punto de vista del cliente y sus hábitos de compra para ver si existe alguna característica anómala en una transacción como, por ejemplo, la hora de la compra. También se pueden analizar los datos de geolocalización junto con los del comercio para analizar si es una compra en un comercio habitual y desde una localización conocida, etc.
60.2 Modelización del fraude en la compra con tarjetas de crédito
El objetivo de este caso de uso es la construcción de un modelo que
permita detectar si una operación de compra realizada con tarjeta de
crédito es fraudulenta o no. Para ello, se utilizará un conjunto de datos
anonimizado de operaciones con tarjeta de crédito ya etiquetadas
disponible desde la web de Kaggle en el siguiente enlace:
https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud.
No obstante, los datos se han incorporado al paquete CDR del libro
con el nombre creditcard.
El conjunto de datos consta de
284.807 transacciones, de las cuales 492 están
etiquetadas como fraudulentas, es decir, solo un 0,172% del total de las
transacciones. Como puede apreciarse, se trata de un dataset muy desequilibrado, lo que
añade cierto grado de dificultad al análisis. El dataset creditcard incluye 31
variables, de las cuales 28 están identificadas como V1, …, V28, una
identificada como Time que registra los segundos transcurridos entre una
transacción y la primera, otra con nombre Amount que registra el importe
de la transacción, y la variable dependiente, class, con
valor 0 para las operaciones no fraudulentas y 1 para las fraudulentas.
Para concluir esta breve descripción del conjunto de datos, es necesario recordar que todos los valores de entrada son numéricos y que ya han sufrido algunas transformaciones. Por motivos de confidencialidad, las variables V1 a V28 no incluyen sus nombres originales ni se añade más información de contexto.
Carga de los datos y obtención de algunos descriptivos
creditcard <- CDR::creditcard
names(creditcard)
#> [1] "Time" "V1" "V2" "V3" "V4" "V5" "V6" "V7"
#> [9] "V8" "V9" "V10" "V11" "V12" "V13" "V14" "V15"
#> [17] "V16" "V17" "V18" "V19" "V20" "V21" "V22" "V23"
#> [25] "V24" "V25" "V26" "V27" "V28" "Amount" "Class"
# psych::describe(creditcard) # descomentar para ver los descriptivosDivisión de los datos
A continuación es necesario dividir los datos en dos dataframes
denominados creditcard_X y creditcard_y. De esta forma, se separan
las variables independientes de la variable dependiente o Class.
# Se dividen los datos
creditcard_X <- creditcard[,-31]
creditcard_y <- creditcard$ClassTratamiento de datos desequilibrados
Uno de los principales problemas a la hora de abordar este tipo de escenarios es lo que se conoce como “datos desequilibrados”. Se dice que un conjunto de datos está desequilibrado cuando la variable dependiente presenta más observaciones de una clase que de otra. En el caso de transacciones con tarjeta de crédito, es evidente que la mayoría de las operaciones son legítimas y que solo un pequeño porcentaje resulta ser fraudulento. ¿Cuál es el problema?
El problema es que, por lo general, los modelos entrenados con conjuntos de datos desequilibrados no se comportan bien cuando tienen que generalizar, es decir, cuando tienen que realizar predicciones sobre conjuntos de datos que no han sido vistos anteriormente por el modelo. El desequilibrio de los datos es un sesgo hacia la clase mayoritaria, por lo que, en última instancia, hay una tendencia al sobreajuste (overfitting) hacia esa clase. Existen diversas técnicas que permiten corregir esta situación:
Undersampling o submuestreo. Esta técnica consiste en reducir el número de observaciones de la clase mayoritaria, estableciendo, por ejemplo, una ratio de 60/40. Esta técnica resulta efectiva si se respetan los grupos naturales que existen en los datos, así como el resto de las características presentes en la clase mayoritaria.
Oversampling o sobremuestreo. Consiste en aumentar el número de observaciones de la clase minoritaria mediante la creación de datos sintéticos que, al igual que la técnica anterior, respeten las características de esa clase.
Para la creación de datos sintéticos con oversampling
existen varios algoritmos que proporcionan buenos resultados. Quizás el
más conocido y utilizado sea Synthetic Minority Oversampling
TEchnique (SMOTE). SMOTE no realiza una copia de las observaciones del
dataset, sino que, en su lugar, genera nuevos datos de forma sintética
utilizando los vecinos más cercanos de esos casos, respetando las
características estadísticas de la clase. Además, los ejemplos de la
clase mayoritaria también son submuestreados, lo que da lugar a un
conjunto de datos más equilibrado. En R, el algoritmo SMOTE está implementado en el
paquete DMwR.
Para este caso de uso particular, se utiliza una técnica simple de
submuestreo implementada en una función del paquete unbalanced. Este paquete no se
encuentra disponible en el repositorio de CRAN por lo que, para su
instalación, se debe ejecutar el siguiente código:
#install.packages("devtools") # descomentar para instalar
library("devtools")
# devtools::install_github("dalpozz/unbalanced") # descomentar para instalar
library("unbalanced")Una vez instalado unbalanced y todas sus dependencias, se realiza el
submuestreo del dataset siguiendo los siguientes pasos:
- Convertir la variable dependiente
Classen factor:
- Ejecutar la función de submuestreo:
undersampled_creditcard <- ubBalance(creditcard_X, creditcard$Class, type='ubUnder', verbose = TRUE)
#> Proportion of positives after ubUnder : 50 % of 984 observations
undersampled_combined <- cbind(undersampled_creditcard$X,
undersampled_creditcard$Y)
names(undersampled_combined)[names(undersampled_combined) == "undersampled_creditcard$Y"] <- "Class"
levels(undersampled_combined$Class) <- c('Legítima', 'Fraude')- Comprobar el número de casos del conjunto de datos sobre el que se ha ejecutado la función de submuestreo:
- Construir el gráfico incluido en la Fig. 60.1 para visualizar el número de elementos de cada clase después de realizar el submuestreo:
library("ggplot2")
ggplot(data = undersampled_combined, aes(fill = Class))+
geom_bar(aes(x = Class))+
ggtitle("Número de casos de cada clase después de submuestreo",
subtitle="Total muestras: 984")+
xlab("")+
ylab("Muestras")+
scale_y_continuous(expand = c(0,0))+
scale_x_discrete(expand = c(0,0))+
theme(legend.position = "ninguna",
legend.title = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank())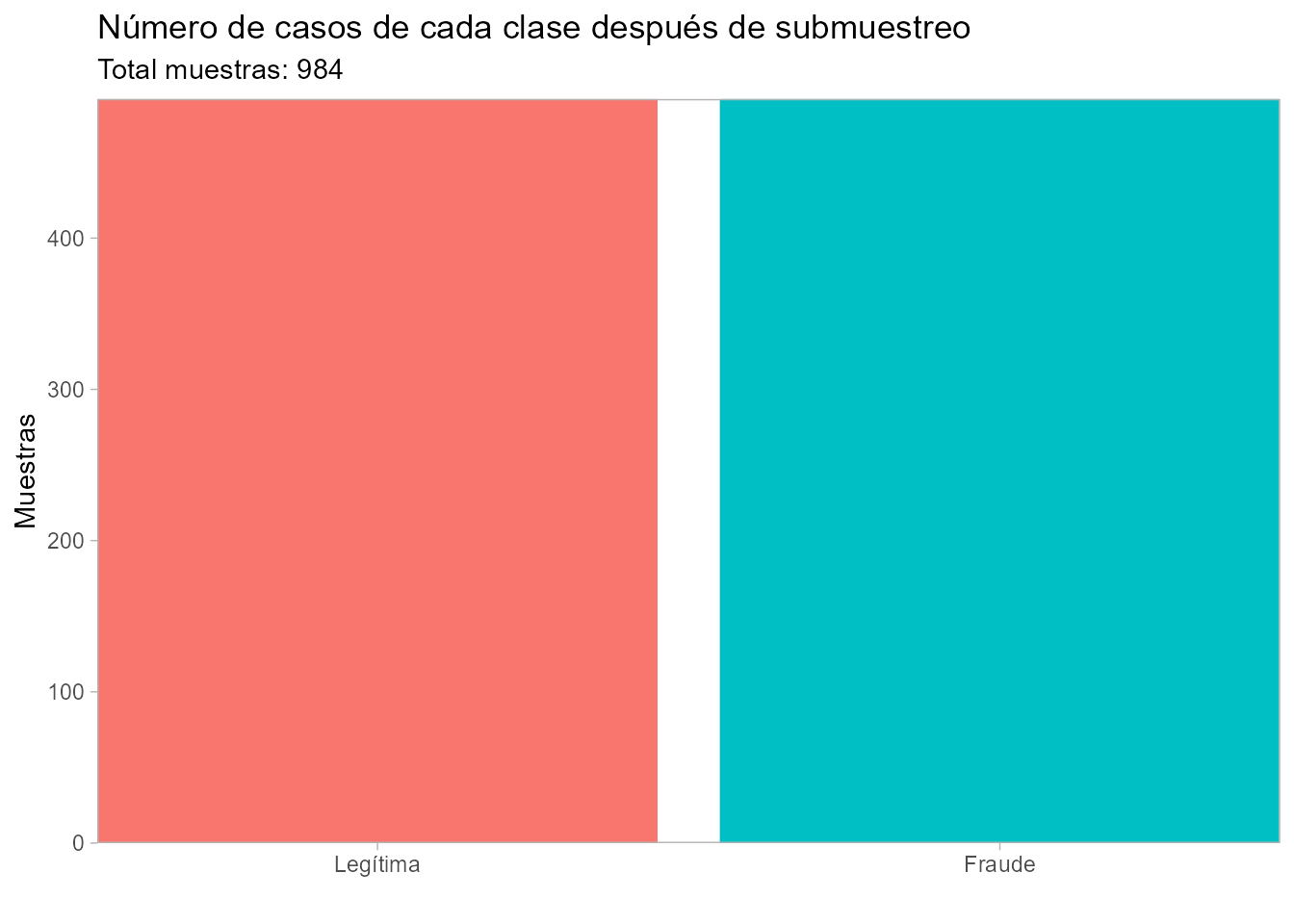
Figura 60.1: Número de casos de cada clase después de submuestreo.
60.2.1 Modelo de clasificación mediante regresión lógística
A continuación se procede a la construcción de un modelo de regresión
logística (véase Cap. 16) para una clasificación binaria
en relación al fraude en transacciones con tarjeta de crédito a partir
de los datos equilibrados obtenidos anteriormente. Por tanto, el dataframe que se utiliza es undersampled_combined, que contiene 984
observaciones, un 50% de las cuales son transacciones identificadas como
fraude.
Lo primero que hay que hacer es realizar un par de pequeños cambios en el dataset; concretamente: \((i)\) eliminar las variables Time y Amount, ya que no son relevantes en el modelo, y \((ii)\) cambiar por 0 y 1 las etiquetas Legitima
y Fraude, respectivamente.
undersampled_combined <- subset( undersampled_combined, select = -c(Time, Amount ) )
undersampled_combined$Class <- ifelse(undersampled_combined$Class == "Fraude",1,0)Lo siguiente será dividir el conjunto de datos en los subconjuntos de
entrenamiento y test, para lo cual se aplica la función split() con
un SplitRatio de 0,80, es decir, un 80% de los datos irá de forma
aleatoria al subconjunto de entrenamiento (788 observaciones) y
el 20% restante (196 observaciones) al subconjunto de test.
#install.packages("caTools") # descomentar para instalar
library("caTools")
set.seed(123)
split = sample.split(undersampled_combined$Class, SplitRatio = 0.80)
training = subset(undersampled_combined, split == TRUE)
test = subset(undersampled_combined, split == FALSE)Una vez en disposición de los subconjuntos de entrenamiento y test, el siguiente paso es entrenar el modelo de regresión logística que clasificará las
transacciones en legítimas o fraudulentas. Para ello se utiliza el
algoritmo GLM, creando un clasificador, que se identificará como
undersampledModel, al que se le pasarán los parámetros siguientes:
• formula: con este parámetro se indica la variable dependiente
seguida del símbolo ~ y un punto (con el punto se hace referencia al
resto de variables del conjunto de datos: V1…V28).
• data: el dataset con los datos de entrenamiento.
• family: al ser un clasificador con dos valores posibles (0, 1), se
indica que será de tipo binomial.
Para ver los resultados del modelo, se ejecutará:
summary(undersampledModel)
#>
#> Call:
#> glm(formula = Class ~ ., family = binomial(), data = training)
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.0920 1.3124 0.832 0.405363
#> V1 -12.0750 3.4119 -3.539 0.000401 ***
#> V2 12.0144 3.4016 3.532 0.000412 ***
#> V3 -28.1234 7.7615 -3.623 0.000291 ***
#> V4 17.9644 4.6995 3.823 0.000132 ***
#> V5 -19.0196 5.3363 -3.564 0.000365 ***
#> V6 -6.7454 1.8440 -3.658 0.000254 ***
#> V7 -36.2314 10.1362 -3.574 0.000351 ***
#> V8 7.8748 2.3570 3.341 0.000835 ***
#> V9 -18.3555 5.0350 -3.646 0.000267 ***
#> V10 -43.2512 11.6981 -3.697 0.000218 ***
#> V11 30.2231 8.1775 3.696 0.000219 ***
#> V12 -54.7049 14.7715 -3.703 0.000213 ***
#> V13 0.3223 0.2690 1.198 0.230828
#> V14 -56.9764 15.3235 -3.718 0.000201 ***
#> V15 -0.9780 0.3600 -2.717 0.006592 **
#> V16 -51.0938 13.8498 -3.689 0.000225 ***
#> V17 -91.4429 25.1048 -3.642 0.000270 ***
#> V18 -34.0561 9.3563 -3.640 0.000273 ***
#> V19 11.0537 3.0811 3.588 0.000334 ***
#> V20 6.6898 1.8617 3.593 0.000326 ***
#> V21 7.7003 2.1177 3.636 0.000277 ***
#> V22 1.0883 0.3687 2.952 0.003158 **
#> V23 -1.1282 0.2954 -3.819 0.000134 ***
#> V24 -0.1794 0.4778 -0.375 0.707307
#> V25 1.8691 0.6880 2.717 0.006595 **
#> V26 0.5692 0.4995 1.140 0.254494
#> V27 9.8047 2.5587 3.832 0.000127 ***
#> V28 4.9230 1.2884 3.821 0.000133 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 1092.40 on 787 degrees of freedom
#> Residual deviance: 172.11 on 759 degrees of freedom
#> AIC: 230.11
#>
#> Number of Fisher Scoring iterations: 18Con el modelo ya entrenado, se realizan las predicciones para los datos
del subconjunto de test, utilizando para ello la función predict().
Los parámetros son simples: el primero es el modelo o clasificador que
se va a utilizar y que será undersampledModel; a continuación el tipo
de dato que devolverá, en este caso response: las probabilidades de fraude listadas en un único
vector que estará disponible a partir de la variable fraud_prob;
y, por último, el parámetro newdata, que hace referencia al dataset en
el que se descarta la última columna por ser la que representa la
variable dependiente.
fraud_prob = predict(undersampledModel, type = "response",
newdata = test[,-29])
head(fraud_prob)
#> 624 3862 6109 6330 6337 6447
#> 0.88543511 0.03196108 1.00000000 0.99999939 1.00000000 1.00000000La visualización del vector con las predicciones puede parecer algo
confusa, por lo que, a menudo, es preciso realizar una conversión de
esas predicciones en valores 0 y 1, dependiendo del rango de valores a
partir del cual se estime que una transacción es fraudulenta: por
ejemplo, a partir del 60% de probabilidad, la transacción será
etiquetada como “1”; en caso contrario será etiquetada como “0”. Para
ello se utiliza la función ifelse:
y_pred = ifelse(fraud_prob > 0.6, 1, 0)La matriz de confusión
Como último paso del ejercicio se crea la matriz de confusión con el fin
de visualizar qué tal se ha comportado el algoritmo, es decir, cuántos
positivos y negativos ha logrado predecir correctamente. Para ello se
crea la variable confusionMatrix, en la cual se almacenará el
resultado de la comparación entre el vector del suconjunto de test, es
decir, los datos etiquetados originalmente, y el vector de sus
traducciones a 0 y 1, resultado del algoritmo. El resultado, como se
puede comprobar, es que ha evaluado correctamente 186 de las 196
observaciones.
confusionMatrix = table(test[, 29], y_pred)
confusionMatrix
#> y_pred
#> 0 1
#> 0 96 2
#> 1 7 91