Capítulo 19 Modelos \(\textit{sparse}\) y métodos penalizados de regresión

María Durbán

Universidad Carlos III de Madrid

19.1 Introducción

El modelo de regresión lineal múltiple: \(y=\beta_0+\beta_1 X_1+\ldots + \beta_pX_p+\varepsilon,\) visto en el Cap. 15, a pesar de su simplicidad, tiene importantes ventajas como la interpretabilidad y su buen poder predictivo en muchas situaciones.

En este capítulo enseña cómo se puede hacer el modelo aún más interpretable y mejor predictor, y para conseguirlo se reemplaza el método de estimación de mínimos cuadrados por un método alternativo. Más concretamente, el objetivo de este capítulo es presentar técnicas para mejorar dos elementos:

• Precisión de la predicción: en particular, cuando el número de variables es mayor que el número de observaciones: \(p>n\) (algo que ocurre con mucha frecuencia hoy en día). En este caso no se pueden utilizar mínimos cuadrados ya que la matriz de diseño no es de rango completo y, por lo tanto, no se puede encontrar una solución única al problema de minimización. Por ello, se necesita reducir el número de variables, que además, evitará que se sobreajusten los datos.
• Interpretabilidad del modelo: al eliminar las variables irrelevantes (es decir, haciendo cero los correspondientes coeficientes) se obtendrá un modelo más fácil de interpretar.

En base a lo anterior, a continuación se presentan varios métodos para llevar a cabo de forma automática la reducción de variables en el modelo, actividad también denominada selección de variables. Tales métodos son:

• Selección del mejor subconjunto: su objetivo es identificar el subconjunto de \(k<p\) predictores que contenga solo los que mejor expliquen el comportamiento de la variable respuesta.
• Shrinkage: en este caso no se quieren seleccionar variables explícitamente, sino que se añade una penalización que penaliza el número de coeficientes o su tamaño.
• Reducción de la dimensión: el objetivo es proyectar los \(p\) predictores en un subespacio de dimensión más pequeña (mediante el uso de combinaciones lineales de las variables predictoras, las cuales se usarán como “nuevos” predictores). Dichas combinaciones lineales se llaman componentes principales y a su análisis se dedica el Cap. 32.

En este capítulo se ven los dos primeros métodos. Para el tercero, se remite al lector al Cap. 32.

19.2 Selección del mejor subconjunto

Supóngase que se tiene acceso a \(p\) variables predictoras, pero se quiere un modelo más simple que involucre solo a un subconjunto de esos \(p\) predictores. La forma lógica de conseguirlo es considerar todos los posibles subconjuntos de los \(p\) predictores y elegir el mejor modelo de entre todos los modelos construidos con cada uno de los subconjuntos de variables. Los pasos a seguir serían:

1. Se crea el modelo nulo, \(M_0\), que es aquel que únicamente contiene la ordenada en el origen y ningún predictor. Este modelo simplemente predice la media muestral para cada observación.

2. Para cada valor de \(k=1,2,\ldots , p\), se calculan los \(\binom{p}{k}\) modelos que contienen \(k\) predictores. Es decir, los \(p\) modelos que contienen 1 predictor, los \(p\times (p-1)/2\) modelos que contienen 2 predictores, etc.

3. Para cada valor de \(k\), se elige el mejor entre los \(\binom{p}{k}=\frac{p!}{(p-k)!k!}\) posibles modelos y se denota por \(M_k\). Es decir, \(M_1\) sería el mejor modelo entre los \(p\) modelos con una única variable, \(M_2\) sería el mejor modelo entre los modelos con dos variables, etc. En este caso, el mejor modelo sería aquel cuya RSS (suma de residuos al cuadrado) sea menor, o equivalentemente, aquel cuyo \(R^2\) sea mayor.

4. Finalmente, entre los modelos: \(M_1,\ldots ,M_p\) se elige el mejor utilizando un criterio como AIC (criterio de información de Akaike), BIC (criterio de información bayesiano) o \(R^2\) ajustado.

Este método se puede usar también en el caso de los GLM, si bien, en este caso, se usa la deviance en vez de RSS.

19.2.1 Procedimiento con R: la función regsubset()

En esta subsección se aplica el método descrito al conjunto de datos Hitters del paquete ISRL2. El objetivo es predecir el sueldo, Salary, de jugadores de béisbol a partir de varias variables asociadas con su rendimiento el año anterior.

La variable Salary no está disponible para algunos de los jugadores. Estos se pueden identificar con la función is.na(). La función sum() permite ver cuántos hay. Se utiliza na.omit() para eliminarlos.

library("ISLR2")
Hitters <- na.omit(Hitters)

La función regsubsets() del paquete leaps lleva a cabo la selección del mejor subconjunto de variables predictoras, identificando el mejor modelo que contiene un número dado de ellas (1,2,3, etc.) atendiendo a RSS. La sintaxis usada es similar a la de la función lm().

library("leaps")
regfit_full <- regsubsets(Salary ~ ., Hitters)

Los resultados pueden verse usando summary(), donde se muestra el mejor modelo para cada número específico de variables. Las variables incluidas en cada modelo se indican con un asterisco. Por ejemplo, el mejor modelo con dos variables incluye Hits y CRBI. Por defecto, regsubsets() solo muestra los resultados de los modelos que contienen hasta ocho variables. La opción nvmax se puede usar para incrementar esta cantidad, por ejemplo hasta 19 variables (que es el número de variables predictoras en el conjunto de datos):

regfit_full <- regsubsets(Salary ~ .,
  data = Hitters,
  nvmax = 19
)
reg_summary <- summary(regfit_full)

La función summary() devuelve diferentes medias de bondad de ajuste: \(R^2\), RSS, \(R^2\) ajustado, \(C_p\) y BIC que se utilizan para elegir el mejor de entre todos los modelos.

names(reg_summary)
#> [1] "which"  "rsq"    "rss"    "adjr2"  "cp"     "bic"    "outmat" "obj"
reg_summary$adjr2
#>  [1] 0.3188503 0.4208024 0.4450753 0.4672734 0.4808971 0.4972001 0.5007849
#>  [8] 0.5137083 0.5180572 0.5222606 0.5225706 0.5217245 0.5206736 0.5195431
#> [15] 0.5178661 0.5162219 0.5144464 0.5126097 0.5106270

En el ejemplo, el \(R^2\) ajustado mayor corresponde al modelo con 11 variables.

Los resultados también se se pueden mostrar y dibujar simultáneamente; por ejemplo, los valores de RSS y \(R^2\) ajustado de todos los modelos se muestran en la Fig. 19.1.

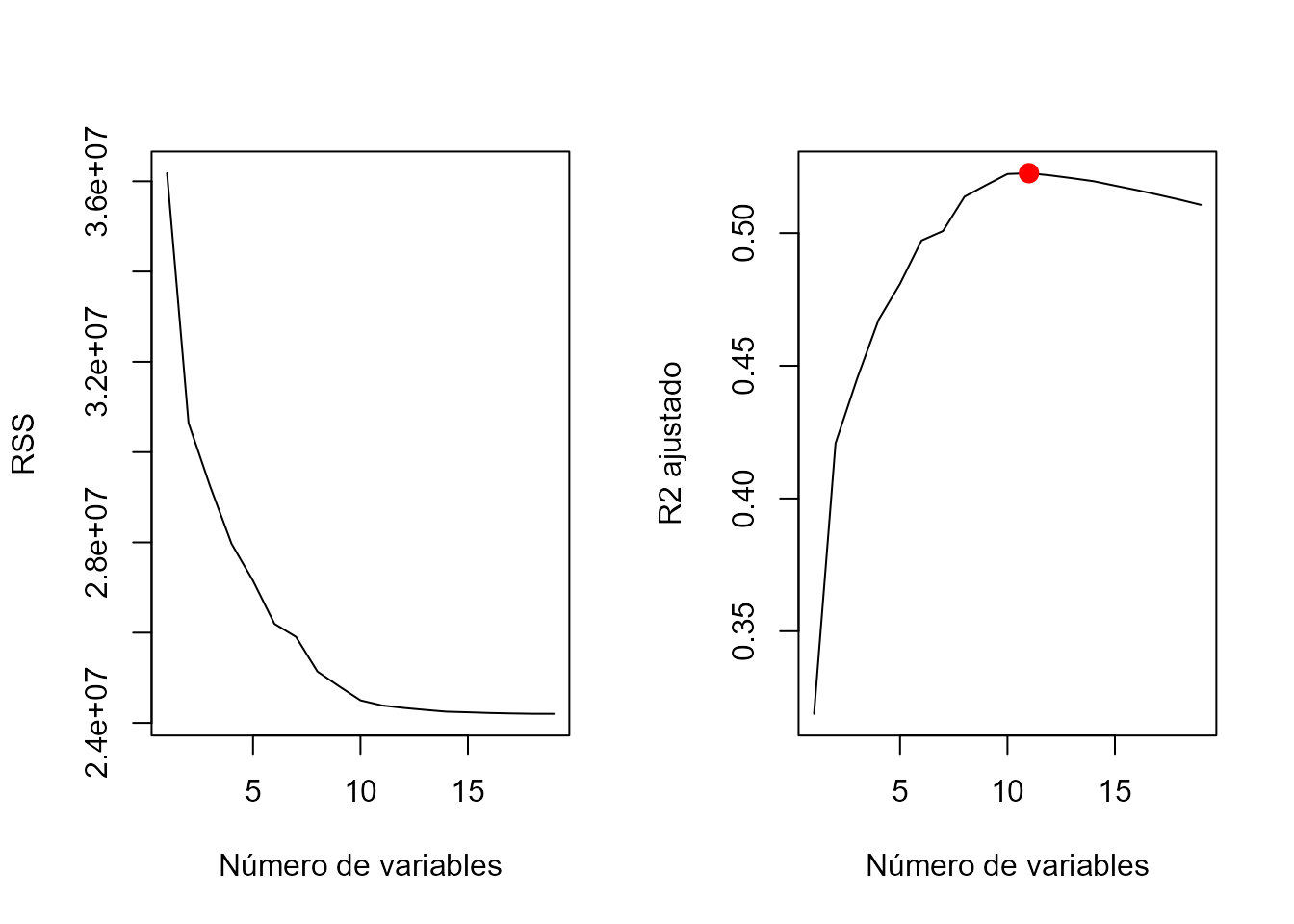
Figura 19.1: Valores de \(R^2\) y \(R^2\) ajustados correspondientes a modelos con distinto número de variables.

Otra manera de visualizar los resultados es:

plot(regfit_full, scale = "adjr2")

Figura 19.2: Variables seleccionadas en cada uno de los modelos y su correspondiente valor de \(R^2\) ajustado.

La primera fila tiene un cuadrado negro en cada una de las variables explicativas del modelo con mayor \(R^2\) ajustado (en este caso, sería similar para los otros criterios).

Varios modelos tienen un valor de \(R^2\) ajustado próximo a \(0.52\), pero es el modelo con 11 variables el que alcanza el mayor valor. La función coef() permite ver los coeficientes estimados de este modelo.

coef(regfit_full, 11)
#>  (Intercept)        AtBat         Hits        Walks       CAtBat        CRuns 
#>  135.7512195   -2.1277482    6.9236994    5.6202755   -0.1389914    1.4553310 
#>         CRBI       CWalks      LeagueN    DivisionW      PutOuts      Assists 
#>    0.7852528   -0.8228559   43.1116152 -111.1460252    0.2894087    0.2688277

19.2.2 Selección stepwise

Cuando el número de variables predictoras, \(p\), es grande, el método anterior es computacionalmente muy costoso ya que el número de posibles combinaciones de variables crece de una manera alarmante. En general, la función regsubset() puede lidiar con hasta 30-40 variables predictoras. Además, otro problema es el sobreajuste. Si se tienen 40 variables, se estarían ajustando millones de modelos, y puede que el modelo elegido funcione muy bien en los datos utilizados para su construcción, pero no tan bien en un nuevo conjunto de datos. Una alternativa es el método stepwise. La idea detrás de este método es similar a la anterior, pero se busca el mejor modelo entre un conjunto mucho más pequeño de modelos.

Hay dos posibilidades de hacer stepwise: forward y backward. Ambas son bastante parecidas; la principal diferencia es el modelo del que se parte: del modelo sin ninguna variable predictora (forward) o del modelo con todas ellas (backward).

19.2.2.1 Forward stepwise

En este caso se comienza con el modelo nulo, \(M_0\), y se van añadiendo variables secuencialmente. En particular, en cada paso (step) la variable que proporciona la mayor mejora al ajuste es la que se añade al modelo. Los pasos a seguir serían:

1. Se crea el modelo nulo, \(M_0\).

2. Para cada valor de \(k=0,1,2,\ldots , p\):

   a) Se consideran todos los \(p-k\) modelos que surgen de aumentar el modelo \(M_k\) con un predictor.

   b) Se elige el mejor de esos \(p-k\) modelos, que se denota \(M_{k+1}\). El término mejor significa tener el RSS más bajo o el \(R^2\) más alto.

3. Se elige el mejor de los modelos \(M_0,\ldots ,M_p\) en función de un criterio que tenga en cuenta la complejidad del modelo, como AIC, BIC o \(R^2\) ajustado.

Este enfoque tiene ventajas computacionales claras, ya que el número de modelos ajustados es mucho menor, pero no garantiza que el modelo elegido sea el mejor modelo posible, especialmente si existe correlación entre las variables predictoras.

19.2.2.2 Backward stepwise

En este caso, se comienza con el modelo que incluye las \(p\) las variables predictoras y se van eliminando de forma iterativa hasta llegar al modelo nulo (\(M_0\)). Los pasos serían:

1. Se ajusta el modelo \(M_p\), que contiene todas (\(p\)) las variable predictoras.
2. Para cada valor de \(k=p,p-1,\ldots , 1\): a) Se consideran todos los \(k\) modelos que surgen de reducir en el modelo \(M_k\) un predictor, es decir, modelos con \(k-1\) variables predictoras. b) Se elige el mejor de esos \(k\) modelos, que se denota \(M_{k-1}\). Dicho modelo será el que tenga el RSS más bajo o el \(R^2\) más alto.
3. Entre los modelos \(M_0,\ldots ,M_p\) se elige el mejor en función de un criterio como AIC, BIC o \(R^2\) ajustado.

Tanto en el caso forward como en el caso backward, se busca el mejor modelo “solo” entre \(1+p(p+1)/2\) modelos, lo que los hace recomendables frente a la selección del mejor subconjunto de variables cuando \(p\) es demasiado grande..

El método backward stepwise necesita que el número de observaciones \(n\) sea mayor que el de variables predictoras \(p\) (ya que necesita ajustar el modelo con todas las variables). Por el contrario, el método forward stepwise se puede usar incluso cuando \(n<p\).

19.2.3 Procedimiento con R: la función regsubset()

La función regsubset() permite utilizar los métodos forward y backward, usando los argumentos method = "forward" o method = "backward":

regfit_fwd <- regsubsets(Salary ~ .,
  data = Hitters,
  nvmax = 19, method = "forward"
)
regfit_bwd <- regsubsets(Salary ~ .,
  data = Hitters,
  nvmax = 19, method = "backward"
)

Los métodos del mejor subconjunto de variables, forward stepwise y backward stepwise no tienen por qué seleccionar el mismo (mejor) modelo. Ni siquiera tienen por qué seleccionar el mismo modelo para cada número de predictores en la fase previa a la selección final. Así ocurre, por ejemplo, cuando el número de variables predictoras es \(k=2\):

coef(regfit_full, 2)
#> (Intercept)        Hits        CRBI 
#> -47.9559022   3.3008446   0.6898994
coef(regfit_fwd, 2)
#> (Intercept)        Hits        CRBI 
#> -47.9559022   3.3008446   0.6898994
coef(regfit_bwd, 2)
#> (Intercept)        Hits       CRuns 
#> -50.8174029   3.2257212   0.6614168

En la etapa final de selección, el modelo seleccionado no tiene por qué ser el mismo en función de los distintos criterios de selección (aunque normalmente lo es). Lo habitual es decidir un criterio para elegir el mejor modelo (\(R^2\) ajustado, BIC, etc.) y seleccionarlo en función de él. En el ejemplo, seleccionando el criterio del \(R^2\) ajustado, el mejor modelo es el que tiene 11 variables, tanto con el criterio forward como con el backward:¹⁴⁸

which.max(summary(regfit_fwd)$adjr2)
#> [1] 11
which.max(summary(regfit_bwd)$adjr2)
#> [1] 11

Con el criterio BIC también se selecciona el modelo con 11 variables predictoras:

which.min(summary(regfit_fwd)$bic)
#> [1] 6
which.min(summary(regfit_bwd)$bic)
#> [1] 8

Otra posibilidad es utilizar como criterio de selección el error de predicción, y para ello se puede echar mano de algún esquema de validación cruzada. A continuación se ilustra el caso en el que se divide la muestra en dos subconjuntos: training y testing, pero se puede utilizar cualquier otro método (validación cruzada \(k-\)grupos, etc). Véase Sec. 10.4.

set.seed(1)
entreno <- sample(c(TRUE, FALSE), nrow(Hitters), replace = TRUE)
test <- (!entreno)

Se utiliza regsubsets() en la muestra de entrenamiento para obtener los modelos con distinto número de variables predictoras:

regfit_best <- regsubsets(Salary ~ ., data = Hitters[entreno, ], nvmax = 19)

Para calcular el error de predicción, dado que la función regsubset() no tiene asociada una función predict(), se han de calcular “manualmente” los valores predichos para la muestra de test. Para eso se necesita la matriz de diseño del modelo.

test.mat <- model.matrix(Salary ~ ., data = Hitters[test, ])

Ahora, para cada modelo de tamaño \(k\), se extraen los coeficientes de regfit_best para el mejor modelo de ese tamaño, se multiplica el vector de coeficientes por la matriz de diseño y se obtienen las predicciones; a continuación se calcula el error cuadrático medio (MSE).

val_errors <- rep(NA, 19)
for (i in 1:19) {
  coefi <- coef(regfit_best, id = i)
  pred <- test.mat[, names(coefi)] %*% coefi
  val_errors[i] <- mean((Hitters$Salary[test] - pred)^2)
}

Con este criterio, el mejor modelo es el que contiene 7 variables:

val_errors
#>  [1] 164377.3 144405.5 152175.7 145198.4 137902.1 139175.7 126849.0 136191.4
#>  [9] 132889.6 135434.9 136963.3 140694.9 140690.9 141951.2 141508.2 142164.4
#> [17] 141767.4 142339.6 142238.2

19.3 Métodos \(\textit{shrinkage}\)

Los métodos anteriores se basan en el ajuste de modelos mediante mínimos cuadrados ordinarios. Los métodos shrinkage, sin embargo, se basan en una modificación del procedimiento de mínimos cuadrados ordinarios que consiste en añadir una penalización que encoge los coeficientes del modelo (normalmente hacia \(0\)). Una de las ventajas de este tipo de métodos es que reduce la varianza de los coeficientes estimados.

Recuérdese que en el ajuste por mínimos cuadrados las estimaciones de \(\beta_0, \beta_1, \ldots , \beta_p\) son los valores que minimizan: \[RSS=\sum_{i=1}^n \left ( y_i-\beta_0-\sum_{j=1}^p \beta_jx_{ji}\right )^2.\]

19.3.1 Regresión ridge

La regresión ridge¹⁴⁹ añade un término de penalización controlado por un parámetro (que habrá que elegir) que penalizará la magnitud de los coeficientes. Cuanto más grande es el coeficiente mayor es la penalización. En consecuencia, en la regresión ridge la expresión que se minimiza para obtener las estimaciones de los parámetros del modelo es: \[\begin{equation} \sum_{i=1}^n \left ( y_i-\beta_0-\sum_{j=1}^p \beta_jx_{ji}\right )^2+\lambda \sum_{j=1}^p \beta_j^2=RSS+\lambda \sum_{j=1}^p \beta_j^2. \tag{19.1} \end{equation}\] En realidad, lo que se está haciendo es hacer pagar al modelo un precio (en términos de ajuste) por el hecho de que los coeficientes no sean cero, y el precio será tanto mayor cuanto más grande sea la magnitud del coeficiente. A esta penalización se le llama penalización shrinkage porque “anima” a los coeficientes a que se contraigan hacia \(0\) (así es como este método favorece la simplicidad de los modelos). La magnitud de dicha contracción está gobernada por lambda, el parámetro de afinado o regulación (también conocido en la jerga como “de tuneado”). Si \(\lambda=0\), se está en el caso de mínimos cuadrados ordinarios, y cuanto mayor sea \(\lambda\), mayor será el precio a pagar para que esos coeficientes sean distintos de \(0\). Si \(\lambda\) es extremadamente grande, los coeficientes estarán muy próximos a \(0\), para que el segundo término sea pequeño (recuérdese que se minimiza RSS más la penalización). Aunque valores más grandes de los coeficientes proporcionasen un mejor ajuste (y por lo tanto un menor RSS), el término de penalización aumentaría y no se alcanzaría el mínimo. Así pues, \(\lambda\) gobierna el equilibrio entre un buen ajuste del modelo y el tamaño de los coeficientes (y, por ende, el número de coeficientes distintos de cero).

La elección del valor de \(\lambda\) es un punto crucial de este tipo de regresión. Para su determinación se suelen utilizar procedimientos de validación cruzada.

19.3.1.1 Escalado de variables predictoras

Un punto importante en regresión ridge es si las variables predictoras están escaladas o no.

El método de mínimos cuadrados ordinarios es invariante a la escala (scale-invariant), es decir, que si se multiplica una variable predictora \(X_j\) por una constante \(c\), el coeficiente estimado se multiplicada por \(1/c\), pero \(X_j\hat \beta_j\) no cambia. Sin embargo, en el caso de la regresión ridge los coeficientes estimados pueden cambiar sustancialmente ante un cambio de escala (es decir, si se multiplica una variable predictora por una constante), ya que todos los coeficientes forman parte del término de penalización. Por lo tanto, antes de utilizar la regresión ridge (o cualquier método de regularización) es importante estandarizar las variables predictoras, dividiendo cada variable por su desviación estándar, de forma que todas tengan desviación estándar igual a \(1\): \[\tilde x_{ji}= \frac{x_{ji}}{\sqrt{\frac{1}{N}\sum_{j=1}^N (x_{ji}-\overline{x}_{j})^2}}.\] Con esto se consigue que los coeficientes estén en “igualdad de condiciones”.

En muchas ocasiones la regresión ridge da lugar a un menor MSE que el obtenido con mínimos cuadrados ordinarios. Sin embargo, por muy grande que sea \(\lambda\) los coeficientes no serán \(0\), sino que estarán próximos a cero, por lo que este método no es realmente un método de selección de variables.

Sin embargo, la regresión ridge puede ser muy útil cuando hay variables predictoras altamente correlacionadas pero se desea mantener todas en el modelo. En estos casos, la regresión ridge soluciona los problemas de multicolinealidad.

19.3.1.2 Procedimiento con R: la función glmnet()

Para llevar a cabo la regresión ridge (y para otros métodos de regresión shrinkage) se usa el paquete glmnet. La función principal en este paquete se llama también glmnet(). Esta función tiene una sintaxis un poco diferente a las funciones usuales para el ajuste de distintos modelos en R. Es necesario pasarle la matriz \(\bf X\) de variables predictoras (sin la columna correspondiente a la ordenada en el origen) y el vector \(\bf y\) con la variable respuesta. Para ilustrar su uso se utilizan los datos anteriores sobre béisbol.

x <- model.matrix(Salary ~ ., Hitters)[, -1]
y <- Hitters$Salary

La función glmnet() tiene un argumento, alpha, que determina el tipo de penalización que se añade en el modelo. En el caso de regresión ridge, alpha=0.

Por defecto, la función glmnet() elige de forma automática el rango de valores de \(\lambda\). Sin embargo, a modo ilustrativo, se va a elegir la rejilla de valores que van desde \(\lambda=10^{10}\) hasta \(\lambda=10^{-2}\), cubriendo de esta forma una gran gama de escenarios, desde el modelo nulo (solo la ordenada en el origen) hasta el caso de mínimos cuadrados ordinarios. Más adelante se verá que se puede llevar a cabo el ajuste del modelo para un valor determinado de \(\lambda\) que no esté entre los de la rejilla inicial.

library("glmnet")
grid <- 10^seq(10, -2, length = 100)
ridge_mod <- glmnet(x, y, alpha = 0, lambda = grid)

Por defecto, la función glmnet() estandariza las variables predictoras para que estén en la misma escala. Si por alguna razón no se quisiera hacer, se usaría standardize = FALSE.

Asociado con cada valor de \(\lambda\) hay un vector de coeficientes estimados mediante regresión ridge almacenados en un matriz accesible utilizando coef(). En este caso, el tamaño de la matriz es \(20 \times 100\), donde las \(20\) filas corresponden a cada uno de los predictores más la ordenada en el origen y las 100 columnas a cada valor de \(\lambda\). Lo esperable es que los coeficientes estimados sean más pequeños cuanto mayor sea el valor de \(\lambda\). A continuación, se muestra el valor de los coeficientes cuando \(\lambda = 11.498\), así como la suma de sus cuadrados, \(\sum_{j=1}^p\beta_j^2\):

ridge_mod$lambda[50]
#> [1] 11497.57
sum(coef(ridge_mod)[-1, 50]^2)
#> [1] 40.45739

Por el contrario, si \(\lambda\) es más pequeño, \(705\), el valor de su suma de cuadrados es mucho mayor.

ridge_mod$lambda[60]
#> [1] 705.4802
sum(coef(ridge_mod)[-1, 60]^2)
#> [1] 3261.554

La Fig. 19.3 muestra el efecto de \(\lambda\) en los coeficientes del modelo:

plot(ridge_mod, xvar = "lambda", label = TRUE)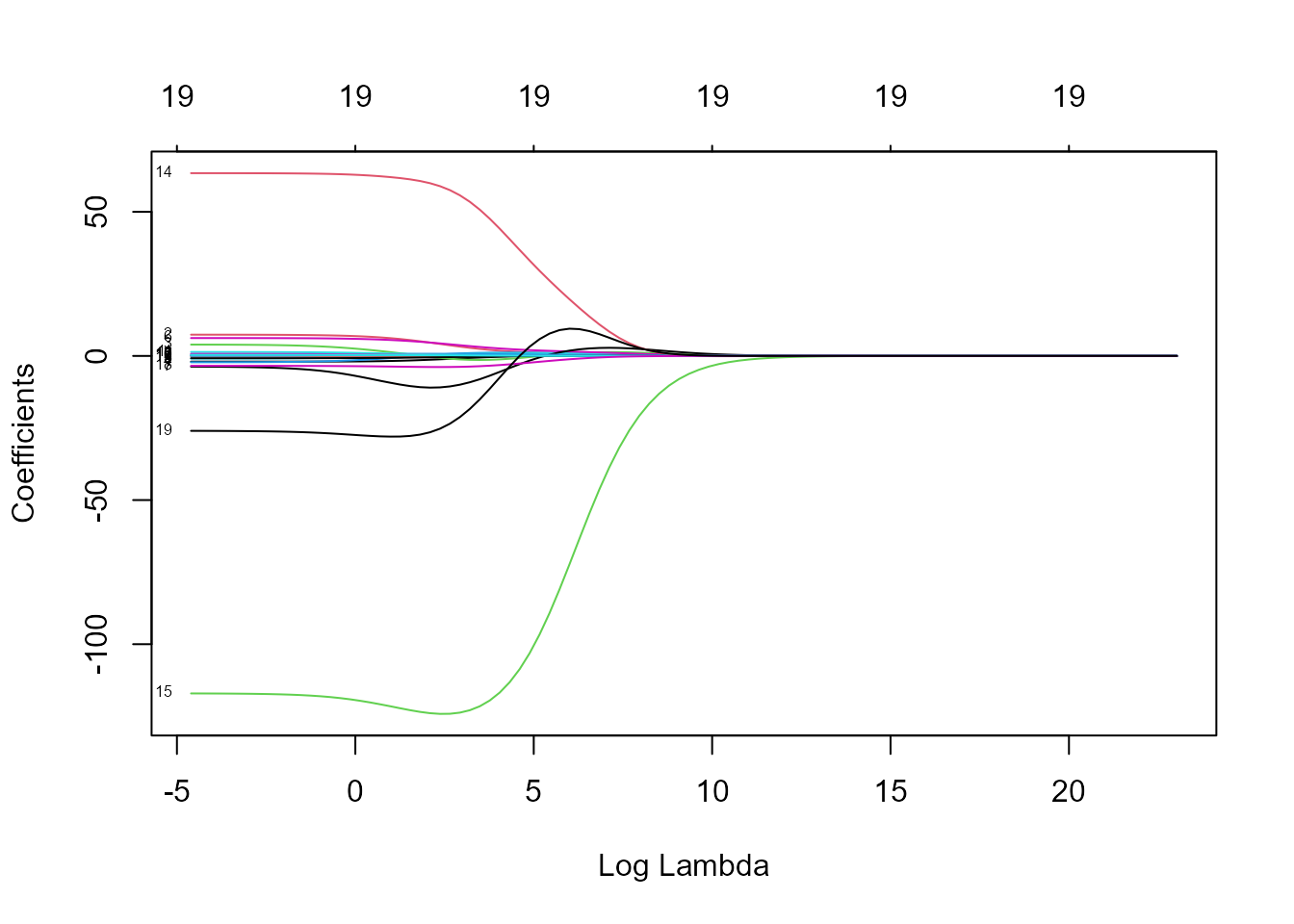

Figura 19.3: Coeficientes estimados para distintos valores del parámetro de penalización (en la escala logarítmica).

El lado izquierdo de la Fig. 19.3 corresponde a valores de \(\lambda\) muy pequeños, y por lo tanto no existen restricciones sobre los coeficientes. Conforme aumenta el valor de \(\lambda\) los coeficientes se aproximan rápidamente a cero. Pero no todos se aproximan a cero de la misma manera: hay un conjunto de variables cuyo coeficiente es prácticamente cero para cualquier valor de \(\lambda\), mientras que para un valor de \(log(\lambda)=3\) parece que hay solo \(4\) coeficientes distintos de \(0\).

La función predict() se puede utilizar con diferentes propósitos. Por ejemplo, se pueden obtener los coeficientes de la regresión ridge para un valor específico de \(\lambda\), por ejemplo \(\lambda=50\):

predict(ridge_mod, s = 50, type = "coefficients")[1:20, ]

En lo que sigue, se ilustra el ajuste de una regresión ridge y se computa el MSE de predicción para distintos valores de \(\lambda\). Primeramente, se divide el conjunto de datos en un subconjunto de entrenamiento y otro de test:

set.seed(1)
entreno <- sample(1:nrow(x), nrow(x) / 2)
test <- (-entreno)
y_test <- y[test]

A continuación se ajusta la regresión ridge a los datos del subconjunto de entrenamiento usando un valor específico de \(\lambda\) (por ejemplo \(\lambda=4\)). Posteriormente, se evalúa su MSE con los datos del subconjunto de test. Para ello se usa la función predict(). En este caso, para obtener las predicciones para la muestra de test, se reemplaza type = "coefficients" por el argumento newx.

ridge_mod <- glmnet(x[entreno, ], y[entreno], alpha = 0, lambda = grid)
ridge_pred <- predict(ridge_mod, s = 4, newx = x[test, ])
mean((ridge_pred - y_test)^2)
#> [1] 142226.5

El MSE es \(142{,}199\). Si se usa un valor muy alto de \(\lambda\), por ejemplo \(10^{10}\) (esto sería equivalente a ajustar un modelo solo con la ordenada en el origen), el resultado es muy distinto:

ridge_pred <- predict(ridge_mod, s = 1e10, newx = x[test, ])
mean((ridge_pred - y_test)^2)
#> [1] 224669.8

Por lo tanto, en este caso, ajustar un modelo de regresión ridge con \(\lambda=4\) da un MSE mucho menor que el obtenido cuando el modelo solo contiene la ordenada en el origen.

A continuación se compara el resultado para \(\lambda=4\) con el obtenido utilizando mínimos cuadrados ordinarios (\(\lambda=0\)).¹⁵⁰

ridge_pred <- predict(ridge_mod, s = 0, newx = x[test, ], exact = T, 
                      x = x[entreno, ], y = y[entreno])
mean((ridge_pred - y_test)^2)
#> [1] 167018.2

Se observa que el MSE es menor cuando se usa regresión ridge (con \(\lambda=4\)) que cuando se usan mínimos cuadrados ordinarios.

Hasta ahora se ha elegido el valor \(\lambda=4\) de forma arbitraria. En la siguiente sección se aborda la cuestión de cómo seleccionar el valor de dicho parámetro de una forma automática.

19.3.2 Selección del parámetro de penalización

En la subsección anterior se ha visto que el valor de \(\lambda\) tiene un gran impacto en los resultados obtenidos cuando se utiliza un modelo con penalización.

Una buena manera de elegir \(\lambda\) es usar validación cruzada (cross-validation). Por ejemplo, se puede usar validación cruzada con 10 grupos (k-fold cross-validation):

• Se dividen los datos en \(k\) grupos, se ajusta el modelo ridge a \(k-1\) de esos grupos (para una rejilla de valores de \(\lambda\)) y se calcula el error de predicción para el otro grupo.
• La acción anterior se repite tomando como muestra de test cada uno de los \(k\) grupos y se suman los errores de predicción.
• Al final se dispondrá de una curva con los errores para cada valor de \(\lambda\) y se elegirá el que dé el mínimo error.

En la práctica, el procedimiento anterior se puede hacer con la función cv.glmnet(). Por defecto, esta función usa un \(10\)-fold cross-validation, pero el número de grupos se puede cambiar usando el argumento nfolds.

En el ejemplo del béisbol:

set.seed(1)
cv_out <- cv.glmnet(x[entreno, ], y[entreno], alpha = 0)
plot(cv_out)

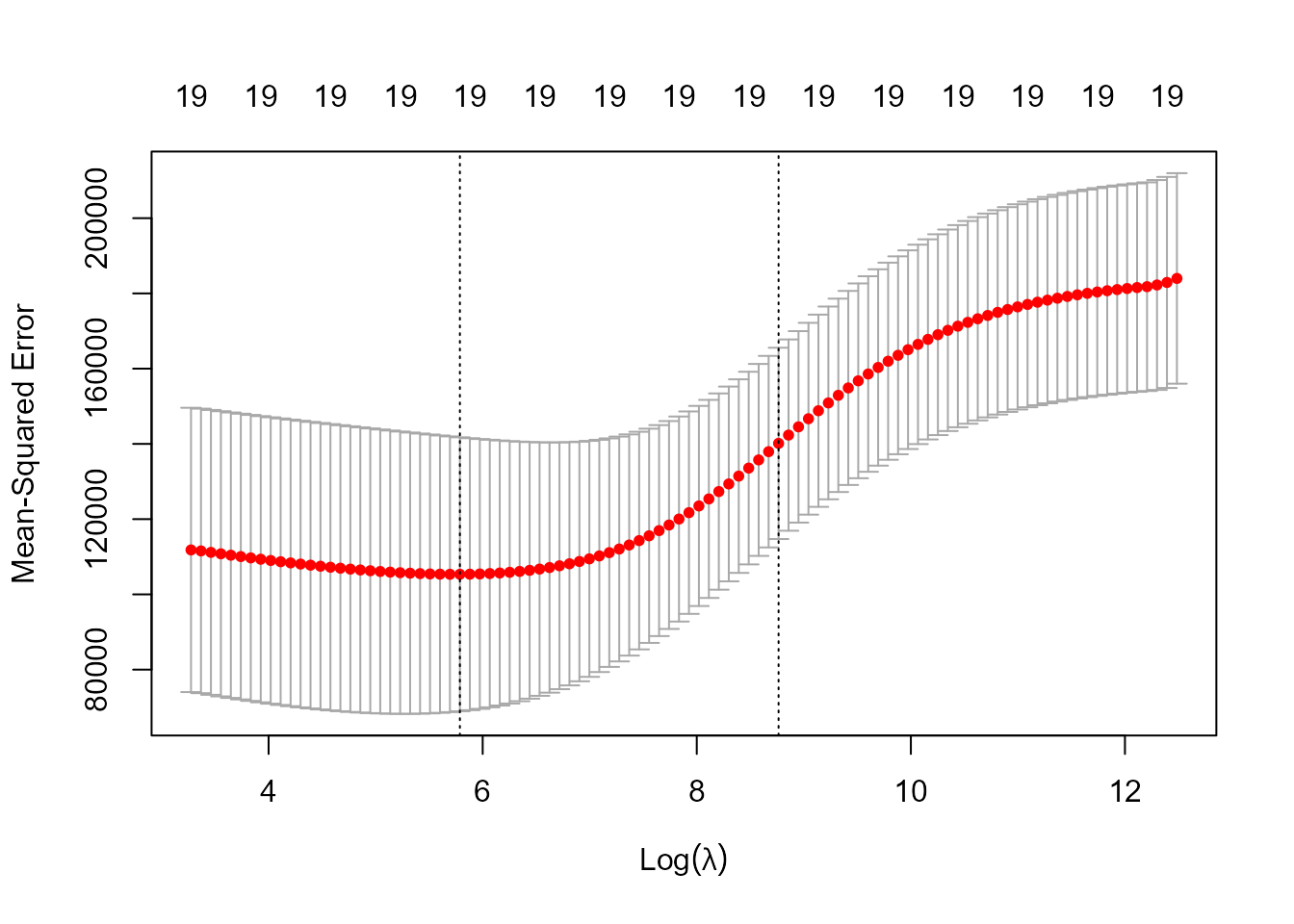
Figura 19.4: Valor del error cuadrático medio y su intervalo de confianza (calculado sobre los 10 grupos) para distintos valores del parámetro de penalización.

mejorlam <- cv_out$lambda.min
mejorlam
#> [1] 326.0828

En la Fig. 19.4, los puntos rojos corresponden a la media del MSE para los 10 grupos y las barras superior e inferior corresponden a esa cantidad más/menos una desviación estándar (el ancho será tanto menor cuanto mayor sea el número de grupos). La primera línea vertical corresponde al valor de \(\lambda\) que hace mínimo el MSE y la segunda es el valor que está a una distancia de una desviación típica del \(\lambda\) mínimo (usar este último valor podría ser una buena opción para evitar el sobre-ajuste, es decir dejar demasiadas variables en el modelo).

El valor mínimo del MSE se calcula como sigue:

ridge_pred <- predict(ridge_mod, s = mejorlam, newx = x[test, ])
mean((ridge_pred - y_test)^2)
#> [1] 139833.6

Como se puede comprobar, hay una apreciable mejora en el error de predicción que se había obtenido cuando el parámetro de penalización se había fijado en \(\lambda=4\).

19.3.3 Regresión Lasso

Uno de los puntos débiles de la regresión ridge es que no hace selección de variables (los coeficientes pueden estar próximos a cero pero no ser exactamente cero). En el modelo final se incluyen todos los coeficientes y, por lo tanto, la regresión ridge solo es útil cuando la mayoría de las variables predictoras tienen un impacto significativo en la respuesta.

La regresión Lasso (least absolute srinkage and selection operator, por sus siglas en inglés), introducida por Tibshirani (1996), es una alternativa a la regresión ridge cuyo objetivo es precisamente corregir la limitación anteriormente mencionada de la regresión ridge, y es útil cuando la mayoría de las variables predictoras no son relevantes en el modelo. Los coeficientes Lasso, \(\hat \beta^L\), minimizan la siguiente cantidad: \[\sum_{i=1}^n \left ( y_i-\beta_0-\sum_{j=1}^p \beta_jx_{ji}\right )^2+\lambda \sum_{j=1}^p |\beta_j|=RSS+\lambda \sum_{j=1}^p |\beta_j|.\] Ahora los coeficientes se contraen hacia cero utilizando la suma de los coeficientes en valor absoluto en vez de la suma de los cuadrados de dichos coeficientes. A esta norma se la llama \(l_1\), \(\|\beta\|_1=\sum_{j=1}^p|\beta_j|\). El cambio que supone es sutil pero importante. En ambos casos los coeficientes se contraen hacia \(0\), pero en el caso de la regresión Lasso cuando \(\lambda\) es suficientemente grande los coeficientes serán \(0\), de modo que se está haciendo una selección de variables. Por consiguiente, la regresión Lasso anulará los coeficientes de las variables que no son importantes a la hora de explicar el comportamiento de la variable respuesta mediante un valor de \(\lambda\) lo suficientemente grande. En este sentido el modelo de regresión Lasso es lo que se llama un modelo sparse (un modelo con un número sparse, o escaso, de parámetros).

¿Por qué Lasso hace que los coeficientes se contraigan exactamente hacia cero? Para entenderlo se va a ver una formulación equivalente a la de los mínimos cuadrados penalizados en el caso de la regresión Lasso: \[\sum_{i=1}^n \left ( y_i-\beta_0-\sum_{j=1}^p \beta_jx_{ji}\right )^2\quad \text{sujeto a} \quad \sum_{j=1}^p |\beta_j|<s.\] Dicha formulación equivalente corresponde a mínimos cuadrados con una restricción, o lo que es lo mismo, con un presupuesto en la norma \(l_1\) sobre los coeficientes. Las dos formulaciones son equivalentes en el sentido de que, si se tiene un presupuesto \(s\), habrá un \(\lambda\) en la primera formulación que corresponda al presupuesto \(s\) en la segunda, y viceversa. Supóngase que se hacen mínimos cuadrados y se obtienen las estimaciones de los parámetros (coeficientes) tales que la suma de sus valores absolutos es 10, pero alguien dice que nuestro presupuesto es \(5\) (la suma de los valores absolutos de los coeficientes no puede ser mayor que esa cantidad). Entonces, hay que resolver el problema de mínimos cuadrados, pero los coeficientes no pueden tomar cualquier valor, ya que se tiene una restricción sobre los mismos. Cuanto más pequeño sea el presupuesto, más próximos a cero serán los coeficientes. Si el presupuesto es \(0\), todos los coeficientes serán también \(0\). Si el presupuesto es muy alto, hay libertad para que los coeficientes tomen el valor que quieran, y se estaría en el caso de mínimos cuadrados. El presupuesto impone que haya un equilibrio entre el ajuste a los datos y el tamaño de los coeficientes.

La Fig. 19.5 (tomada de James et al., 2013) muestra por qué el modelo de regresión Lasso es sparse. El gráfico corresponde a un modelo de regresión con dos variables predictoras. El punto donde está el vector de coeficientes, \(\hat{\boldsymbol{\beta}}\), es donde se alcanza el valor mínimo de la suma de los cuadrados de los residuos del modelo (RSS) y los contornos son combinaciones de valores de \(\beta_1\) y \(\beta_2\) que dan lugar al mismo valor de RSS, pero que ya no sería el mínimo. Las regiones de restricción son \(|\beta_1|+|\beta_2|<s\) (Lasso) y \(\beta_1^2 +\beta_2^2<s\) (ridge). En el caso de la regresión ridge, el presupuesto es el radio del círculo y la regresión ridge busca el primer lugar en el que el contorno toca a la región de restricción, pero, al ser un círculo, difícilmente uno u otro coeficiente va a ser \(0\). En el caso de la regresión Lasso, la región de restricción tiene forma de diamante y, por lo tanto, tiene vértices. Como puede apreciarse, en la Fig. 19.5 el contorno toca a la región de restricción en el caso en que \(\beta_1=0\).

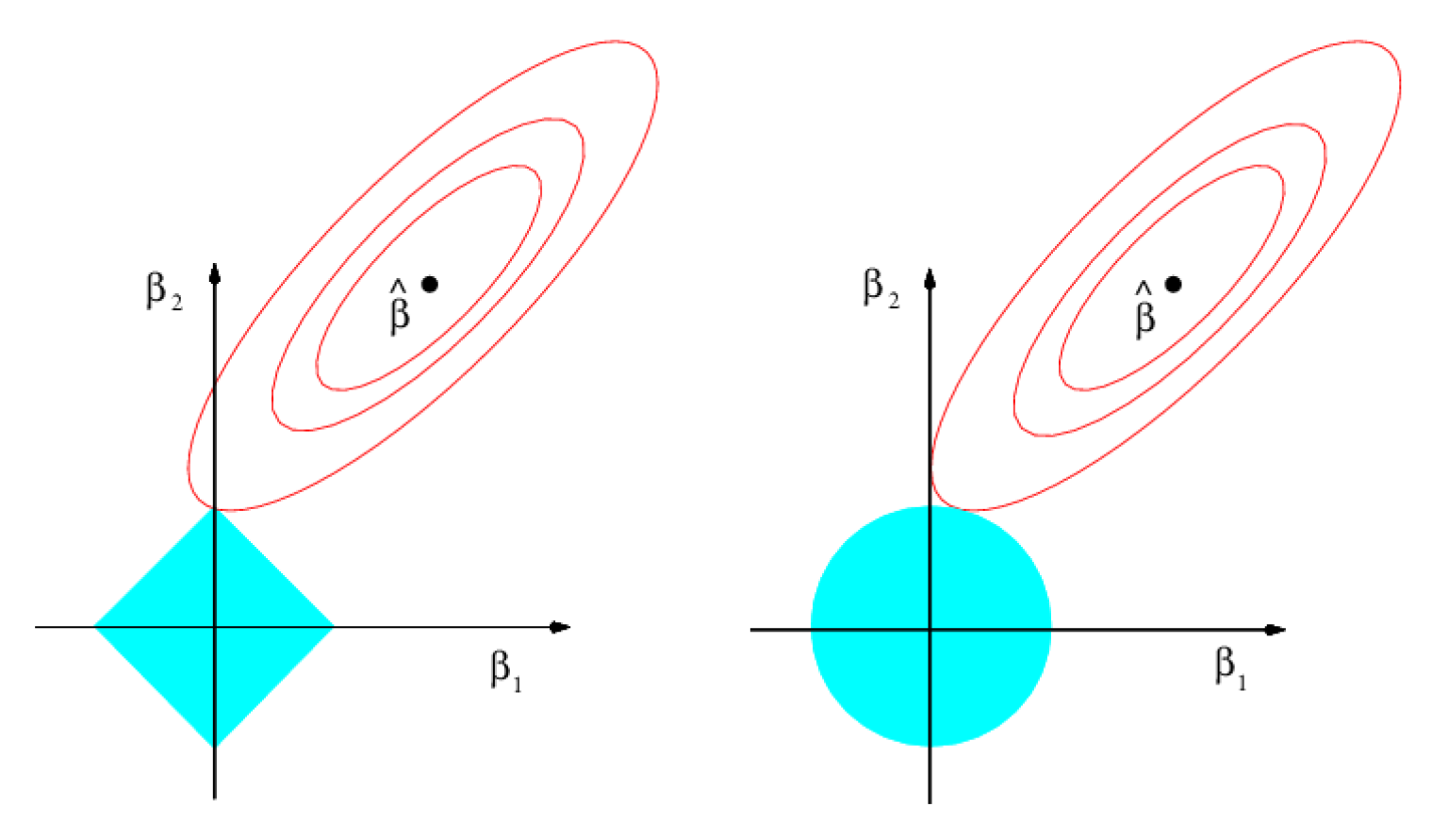
Figura 19.5: Contornos (rojo) de RSS y regiones de restricción (en azul) para la regresión Lasso (izquierda) y \(ridge\) (derecha).

Se vuelve al ejemplo del béisbol para mostrar la regresión Lasso; en este caso el argumento \(\alpha\) toma valor \(1\) (\(0\) en el caso de la regresión ridge).

lasso_mod <- glmnet(x[entreno, ], y[entreno], alpha = 1, lambda = grid)
plot(lasso_mod)

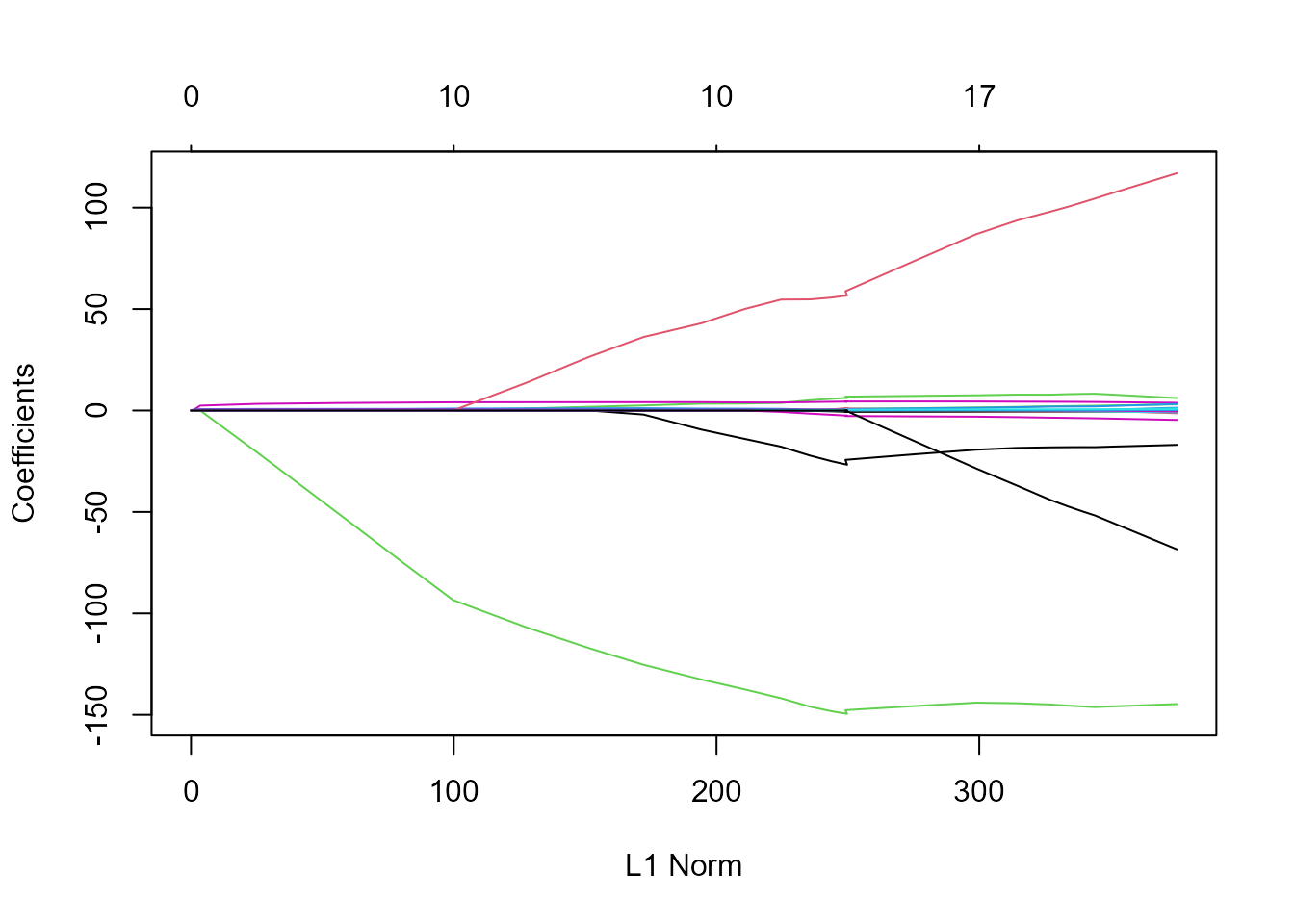
Figura 19.6: Valor de los parámetros estimados para distintos valores de la penalización (que depende del parámetro de penalización).

En la Fig. 19.6 se puede ver que, dependiendo del valor del parámetro de penalización, algunos de los coeficientes se hacen exactamente \(0\). Para elegir el valor de dicho parámetro y calcular el MSE resultante en el conjunto de test se procede como sigue:

set.seed(1)
cv_out <- cv.glmnet(x[entreno, ], y[entreno], alpha = 1)
plot(cv_out)

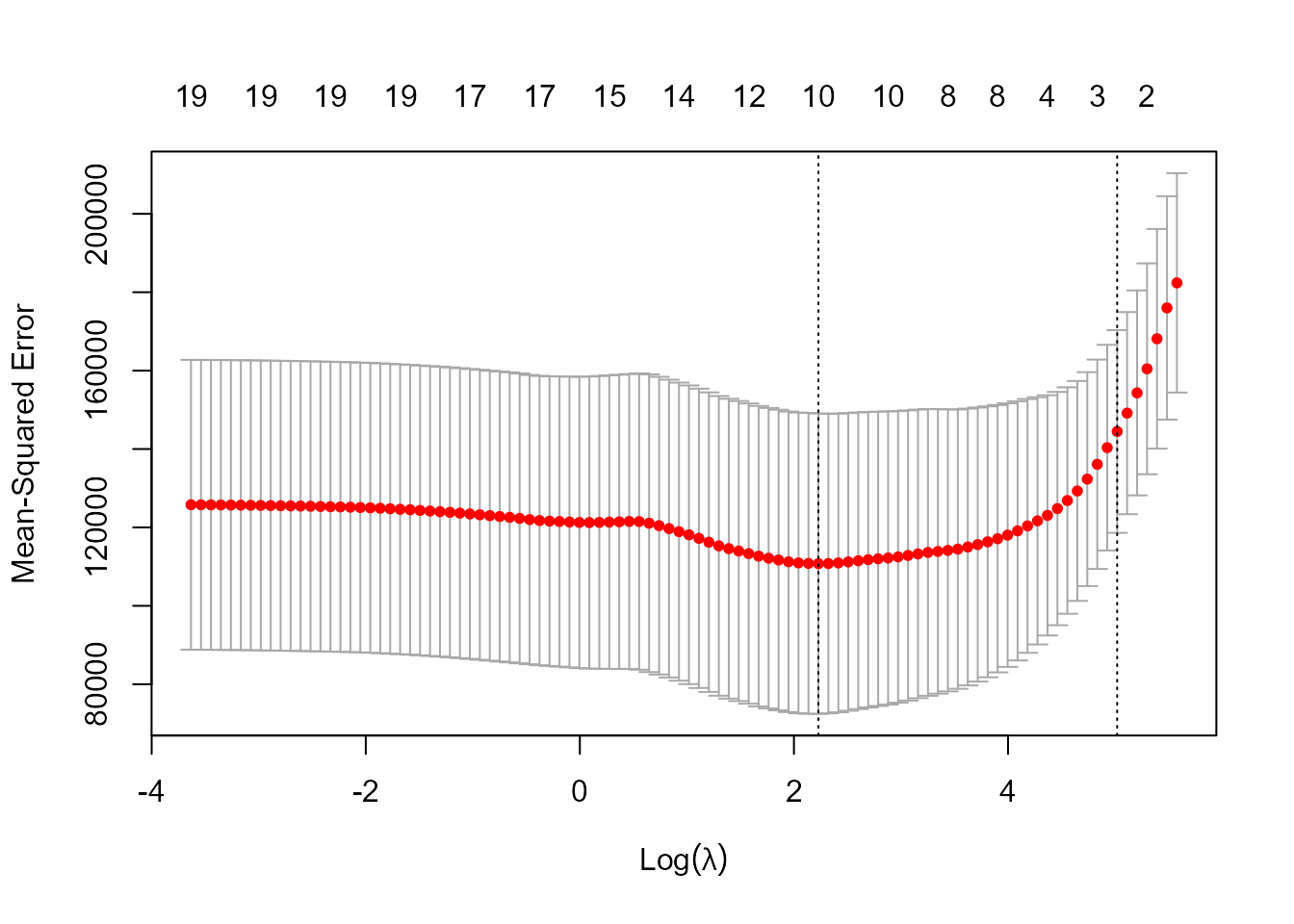
Figura 19.7: Valor del error cuadrático medio y su intervalo de confianza para distintos valores del parámetro de penalización.

mejorlab <- cv_out$lambda.min
lasso_pred <- predict(lasso_mod, s = mejorlab, newx = x[test, ])
mean((lasso_pred - y_test)^2)
#> [1] 143673.6

Este valor es bastante más bajo que MSE en la muestra de test en el caso de mínimos cuadrados ordinarios (224.666,8) y bastante parecido al obtenido con la regresión ridge cuando el parámetro de penalización se elige mediante validación cruzada: 139.856,6). Sin embargo, la regresión Lasso tiene una ventaja importante con respecto a la regresión ridge ya que los coeficientes estimados son sparse. En los resultados que se muestran a continuación, se puede observar que 10 de los 20 coeficientes estimados son \(0\). Por lo tanto, el modelo Lasso con \(\lambda\) elegido mediante validación cruzada contiene solo nueve variables predictoras (Fig. 19.7).

out <- glmnet(x, y, alpha = 1)
lasso_coef <- predict(out, type = "coefficients", s = mejorlab)[1:20, ]
lasso_coef[lasso_coef != 0]
#>   (Intercept)          Hits         Walks        CHmRun         CRuns 
#>   -3.04787656    2.02551572    2.26853781    0.01647106    0.21177390 
#>          CRBI       LeagueN     DivisionW       PutOuts        Errors 
#>    0.41944632   20.48456551 -116.59062083    0.23718459   -0.94739923

19.3.4 Elastic net

Uno de los problemas de la regresión Lasso es cuando hay variables predictoras correlacionadas entre sí, pues elegirá una de ellas (y los coeficientes de las demás los hará cero) sin un criterio objetivo. Además, supóngase que se está en una situación en la que el número de variables \(p\) es mayor que el número de observaciones \(n\); en este caso la regresión Lasso elegiría como mucho \(n\) variables; mientras que la regresión ridge las utilizaría todas, aumentando la complejidad del modelo (esto en algunos casos puede ser lo deseable o no). Elastic net (Zou & Hastie, 2005) es una generalización de los métodos anteriores que combina las penalizaciones de las regresiones ridge y Lasso: \[\sum_{i=1}^n \left ( y_i-\beta_0-\sum_{j=1}^p \beta_jx_{ji}\right )^2+\lambda_1 \sum_{j=1}^p \beta_j^2+\lambda_2 \sum_{j=1}^p |\beta_j|.\] También aparece en muchas ocasiones de esta otra forma: \[\sum_{i=1}^n \left ( y_i-\beta_0-\sum_{j=1}^p \beta_jx_{ji}\right )^2+\lambda \left [ \frac{1}{2} (1-\alpha)\sum_{j=1}^p \beta_j^2+\alpha \sum_{j=1}^p |\beta_j|\right ],\] donde \(\alpha\in [0,1]\). El parámetro \(\alpha\) es el que gobierna la combinación de las dos penalizaciones, mientras que \(\lambda\) es el que controla la cantidad de penalización. Si \(\alpha=0\) se está en el caso de la regresión ridge; \(\alpha=1\) lleva a la regresión Lasso.

La función glmnet() también sirve para ajustar elastic net, pero el parámetro \(\alpha\) hay que elegirlo a priori. Otra opción es utilizar el paquete caret para hacer validación cruzada sobre \(\alpha\) y \(\lambda\) simultáneamente:

set.seed(1)
library("caret")
cv_glmnet <- train(
  x = x[entreno, ],
  y = y[entreno],
  method = "glmnet",
  trControl = trainControl(method = "cv", number = 10),
  tuneLength = 10
)
# modelo con el MSE más pequeño
cv_glmnet$bestTune
#>   alpha   lambda
#> 9   0.1 99.12337
ggplot(cv_glmnet)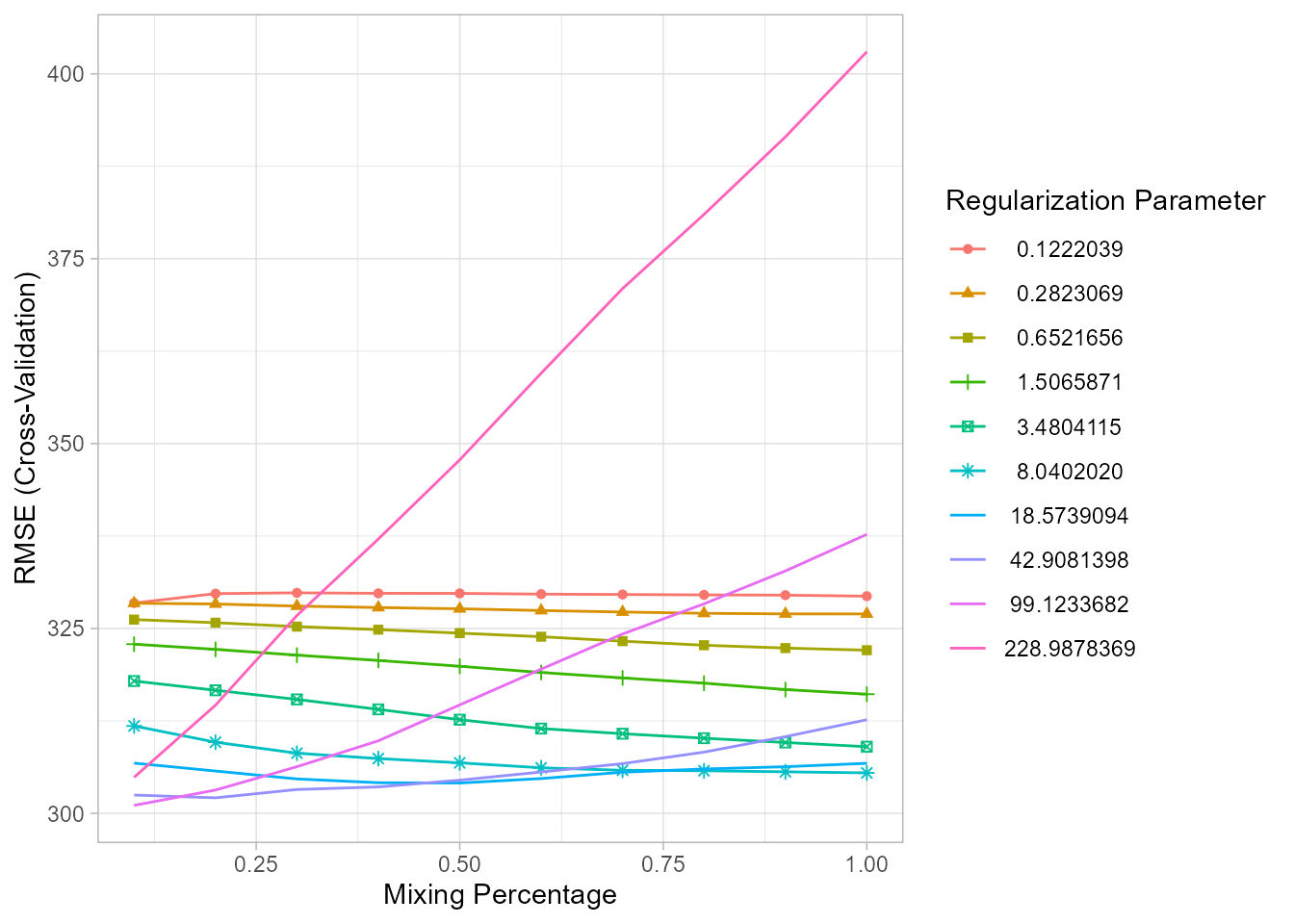

Figura 19.8: Valor de la raíz cuadrada del error cudrático medio para distintas combinaciones de \(\alpha\) y \(\lambda\).

La Fig. 19.8 muestra cómo la combinación de \(\alpha\) y \(\lambda\) da lugar a diferentes MSE (en la figura aparece el RMSE, o sea, su raíz cuadrada). Cada línea corresponde a un valor de \(\lambda\) distinto, y en el eje \(x\) se representan los valores de \(\alpha\).

A continuación se calcula el valor del MSE en el conjunto de test para el modelo elastic net con \(\alpha=0,1\) y \(\lambda=99,337\), que son los valores de \(\alpha\) y \(\lambda\) que hacen mínimo dicho MSE:

elastic_mod <- glmnet(x[entreno, ], y[entreno], alpha = cv_glmnet$bestTune$alpha)
elastic_pred <- predict(elastic_mod, newx = x[test, ], s = cv_glmnet$bestTune$lambda)
mean((elastic_pred - y_test)^2)
#> [1] 141626.1

Como puede comprobarse, es peor que el de la regresión ridge pero mejor que el de Lasso.

Por tanto, si no se quiere hacer ningún tipo de selección se debe estimar una regresión ridge y si se quiere reducir al máximo el número de variables predictoras se debe estimar una regresión Lasso (a costa de que aumente el MSE en el conjunto de test). El equilibrio viene de la mano del modelo elastic net, que hace selección de variables pero no aumenta el MSE de predicción.

Existen otros métodos de penalización que se derivan de estos, como el group Lasso, el sparse group-Lasso, etc. Se puede encontrar información sobre ellos en Hastie et al. (2015).

Resumen

En este capítulo se introducen una serie de técnicas para mejorar la predicción y la interpretabilidad de los modelos de regresión. En particular:

• Se muestra el uso de la técnica de selección del mejor subconjunto de variables en el modelo, así como los métodos stepwise.

• Se presentan 3 métodos tipo shrinkage: regresión ridge, Lasso y elastic net, bien para la selección de variables, bien para solventar problemas de multicolinealidad en el modelo.

• Se muestra cómo seleccionar el parámetro de penalización (o de combinación de penalizaciones en el caso de la regresión elastic net) que controla la regresión penalizada.

• Se ilustra el uso de todas las metodologías propuestas en el capítulo mediante el análisis de un caso práctico.