Capítulo 40 Trabajando con datos espaciales

Gema Fernández-Avilés²⁵⁹

Universidad de Castilla-La Mancha

40.1 Introducción

Los datos espaciales, también conocidos como datos geográficos o datos georreferenciados, son aquellos que contienen información de una localización o área geográfica de la superficie de la Tierra o que están relacionados con dicha localización. Se podría decir también que son aquellos que están anclados al espacio. El primer análisis de datos espaciales fue realizado por el médico John Snow en 1854 (Snow, 1856). Él construyó un famoso mapa que mostraba las muertes causadas por un brote de cólera (que mató a 127 personas en 3 días) en el barrio del Soho de Londres junto con la ubicación de las bombas de agua en el área (véase Fig. 40.1). Snow descubrió que había un agrupamiento significativo de muertes alrededor de una determinada bomba, y al quitar la manija de la bomba se detuvo el brote. Tanto los datos de muertes con los que trabajó Snow como aquellos que contienen las coordenadas de las ubicaciones donde estaban situadas las bombas de agua son datos espaciales.

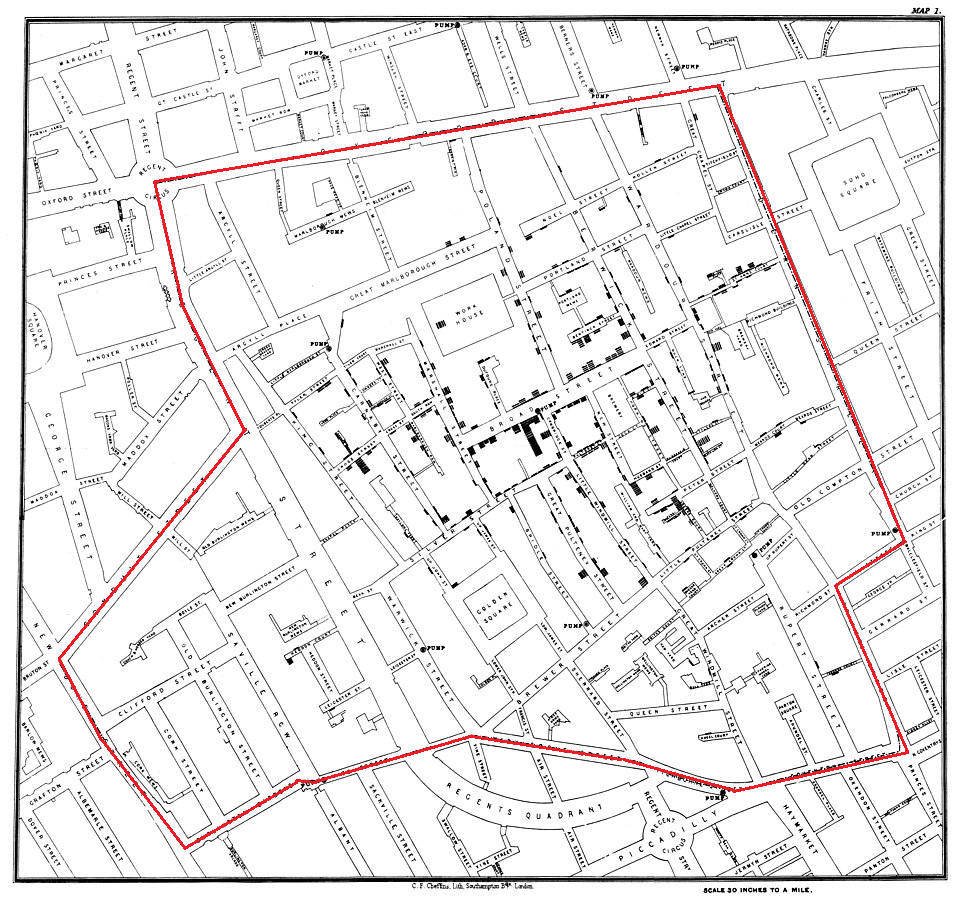
Figura 40.1: Mapa de cólera en Londres según Snow. Fuente: adaptado de Snow (1856).

El análisis espacial de Snow es considerado el antecedente conocido más antiguo de la ciencia de datos (Baumer et al., 2021), porque: (i) la información clave se obtuvo mediante la combinación de tres fuentes de datos (las muertes por cólera, las ubicaciones de las bombas de agua y el mapa de calles de Londres); (ii) se puede crear un modelo espacial directamente a partir de los datos; y (iii) el problema solo se resolvió cuando la evidencia basada en datos se combinó con un modelo plausible que explicaba el fenómeno físico. Es decir, Snow era médico y su conocimiento sobre la transmisión de enfermedades fue suficiente para convencer a sus colegas de que el cólera no se transmitía por el aire.

40.1.1 Estadística para datos espaciales

El área que se encarga de estudiar y analizar los datos espaciales es la estadística espacial o la estadística para datos espaciales (N. A. C. Cressie, 1993; Montero et al., 2015).

Debido a que los datos espaciales surgen en múltiples campos y aplicaciones, hay una gran variedad de tipos de datos, estructuras y escenarios espaciales (Schabenberger & Gotway, 2005). La Fig. 40.2 representa la clasificación de datos espaciales proporcionada por N. A. C. Cressie (1993), basada en la naturaleza del dominio espacial en estudio. Cressie distingue tres tipos de datos espaciales: ($i$) datos geoestadísticos, ($ii$) datos lattice o reticulares y ($iii$) datos de patrones de puntos.

En este libro, el estudio de los datos geoestadísticos se aborda en el Cap. 41, el análisis de los datos lattice se lleva a cabo en el Cap. 42, dedicado a la econometría espacial, y los datos de patrones de puntos se analizan en el Cap. 43.

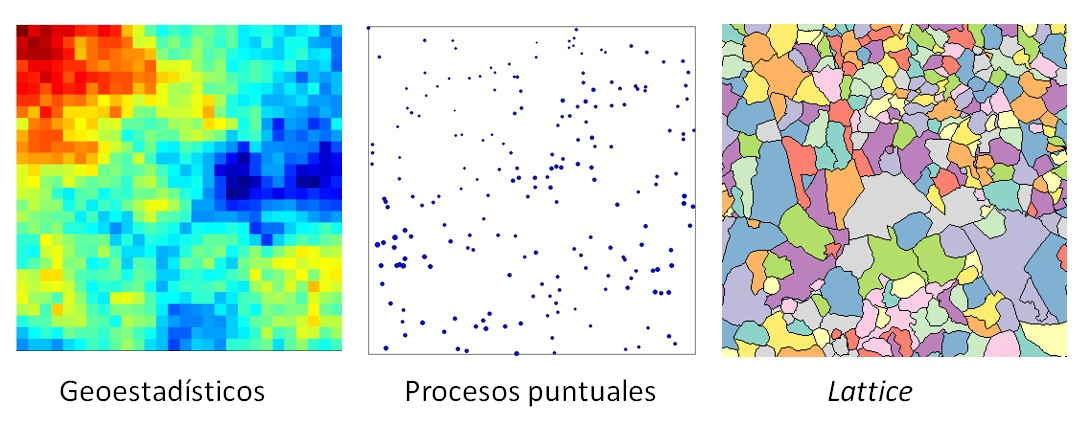
Figura 40.2: Clasificación de datos espaciales propuesta por Cressie (1993).

40.2 Conceptos clave

Visto el contexto original de los datos espaciales, y antes de entrar en detalle en su análisis, se debe tener en cuenta una serie de conceptos clave. La Fig. 40.3 representa la localización de los accidentes de tráfico registrados en la ciudad de Madrid durante el año 2020. Sin embargo, tal representación no aporta información útil para su análisis. Por ejemplo, sería interesante añadir un mapa de carreteras junto con la localización de los accidentes.

library("CDR")
library("tidyverse")
ggplot(data = accidentes2020_data,
       aes(x = coordenada_x_utm, y = coordenada_y_utm)) + 
  geom_point(col="blue", size = 0.1, alpha = 0.3) +
  coord_fixed()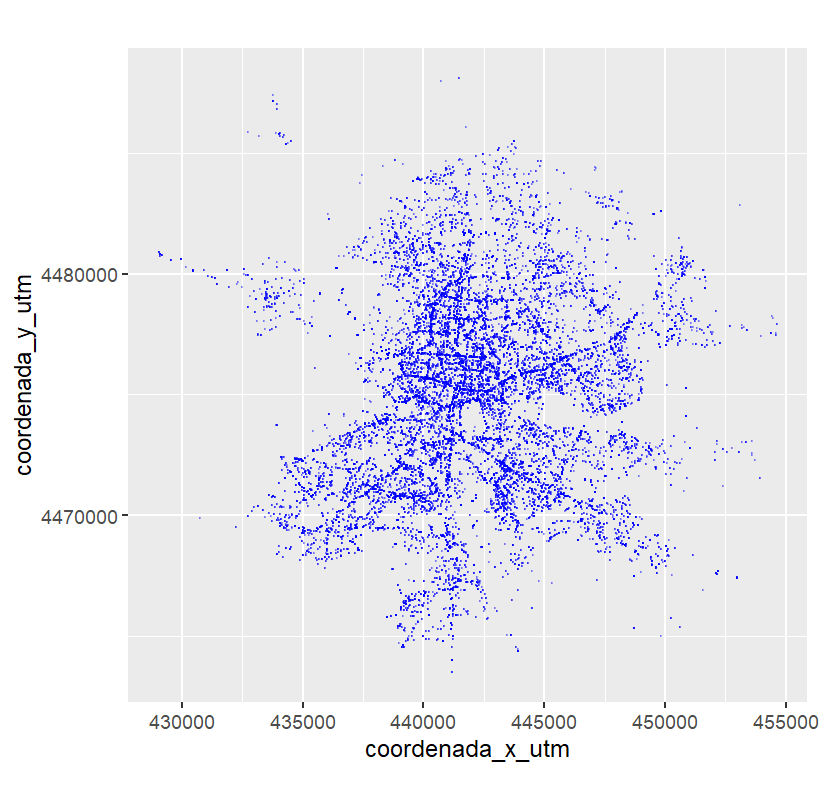

Figura 40.3: Accidentes de tráfico en Madrid (2020).

Además de las coordenadas, en la representación de geodatos es importante el marco o contexto espacial, así como el conocimiento del (i) sistema de referencia de coordenadas o coordinate reference system (CRS) en el que están goerreferenciadas o proyectadas las coordenadas y (ii) el formato de los datos con los que se está trabajando: vector o raster.

library("sf")
accidentes2020_sf <- st_as_sf(accidentes2020_data,
  coords = c("coordenada_x_utm", "coordenada_y_utm"),
  crs = 25830 # proyección ETRS89/ UTM zone 30N. Área de uso: Europa  
  )  

library("mapSpain")
madrid <- esp_get_munic(munic = "^Madrid$") |>
  st_transform(25830) 

# descara imagen de un de mapa estático de las carreteas de Madrid
tile <- esp_getTiles(madrid, "IDErioja", zoommin = 2)  

ggplot() +
  tidyterra::geom_spatraster_rgb(data = tile) +
  geom_sf(data = accidentes2020_sf, 
    col = "blue", size = 0.1, alpha = 0.3) +
  coord_sf(expand = FALSE)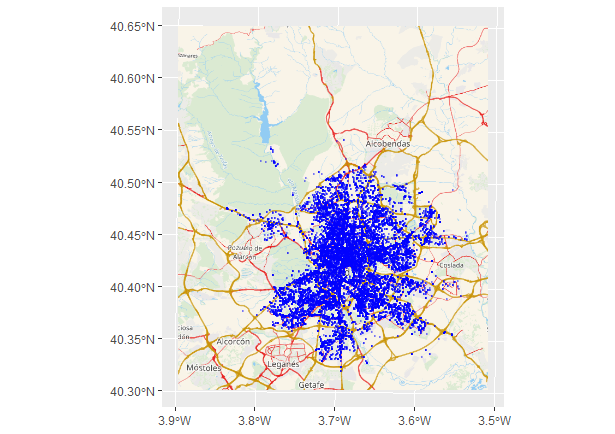

Figura 40.4: Accidentes de tráfico en Madrid proyectados y con mapa de carreteras (2020).

La Fig. 40.4 incluye el marco o contexto espacial (el mapa de carreteras de Madrid) en el que tuvieron lugar los accidentes mostrados en la Fig. 40.3, lo cual permite observar ciertos patrones en la ocurrencia de accidentes. Por ejemplo, apenas se producen accidentes en la Casa de Campo o en el Monte del Pardo y parece observarse cierta concentración en la ciudad y en las autopistas de salida de la ciudad.

40.2.1 Sistema de referencia de coordenadas

Los CRS permiten identificar con exactitud la posición de los datos sobre el globo terráqueo. Cuando se trabaja con datos espaciales procedentes de distintas fuentes de información es necesario comprobar que las coordenadas correspondientes a dichos datos se encuentran definidas en el mismo CRS. Esto se consigue transformándolas (o proyectándolas) a un CRS común. Una buena referencia para profundizar esta cuestión es el Cap. 2 de Pebesma & Bivand (2023).

En la Fig. 40.5 se muestran los puertos en un mapa mundial. Todos vienen representados por el punto rojo. ¿A qué se debe? A que los datos están en distintos CRS.

library("giscoR")

paises <- gisco_get_countries()
puertos <- gisco_get_ports()
paises_robin <- st_transform(paises, st_crs("ESRI:54030")) #Proyección Robinson

plot(st_geometry(paises_robin), main = " ")
plot(st_geometry(puertos), add = TRUE, col="2", pch=20, lwd=2.5)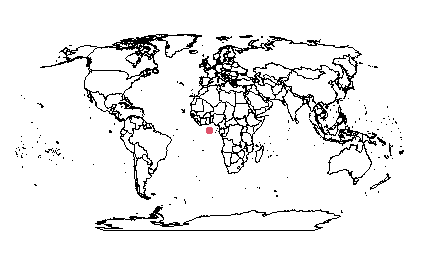

Figura 40.5: Localización de los puertos en el mapamundi (distinto CRS en los puertos y el mapa).

Los dos tipos de CRS que existen se describen a continuación:

Geográficos: aquellos en los que los parámetros empleados para localizar una posición espacial son la latitud (Norte-Sur [$-$90º, 90º]) y la longitud (Este-Oeste [$-$180º, 180º]). Están basados en la geometría esférica. En este caso las distancias entre dos puntos son distancias angulares.²⁶⁰

Proyectados: permiten reducir la superficie de la esfera terrestre (3D) a un sistema cartesiano (2D). Para ello, es necesario transformar las coordenadas longitud y latitud en coordenadas cartesianas $X$ e $Y$. La unidad de distancia, habitualmente, es el metro.

Retomando el ejemplo de los puertos marítimos, tras proyectar los puertos al mismo CRS que el mapamundi utilizando la proyección de Robinson (la proyección cartográfica más popular para mapamundis), la Fig. 40.6 ya muestra adecuadamente la localización de los puertos en el mapamundi.

st_crs(puertos) == st_crs(paises_robin) # Comprueba CRS
#> [1] FALSE
puertos_robin <- st_transform(puertos, st_crs(paises_robin))
plot(st_geometry(paises_robin), main = " ")
plot(st_geometry(puertos_robin), add = TRUE, col=4, pch=20)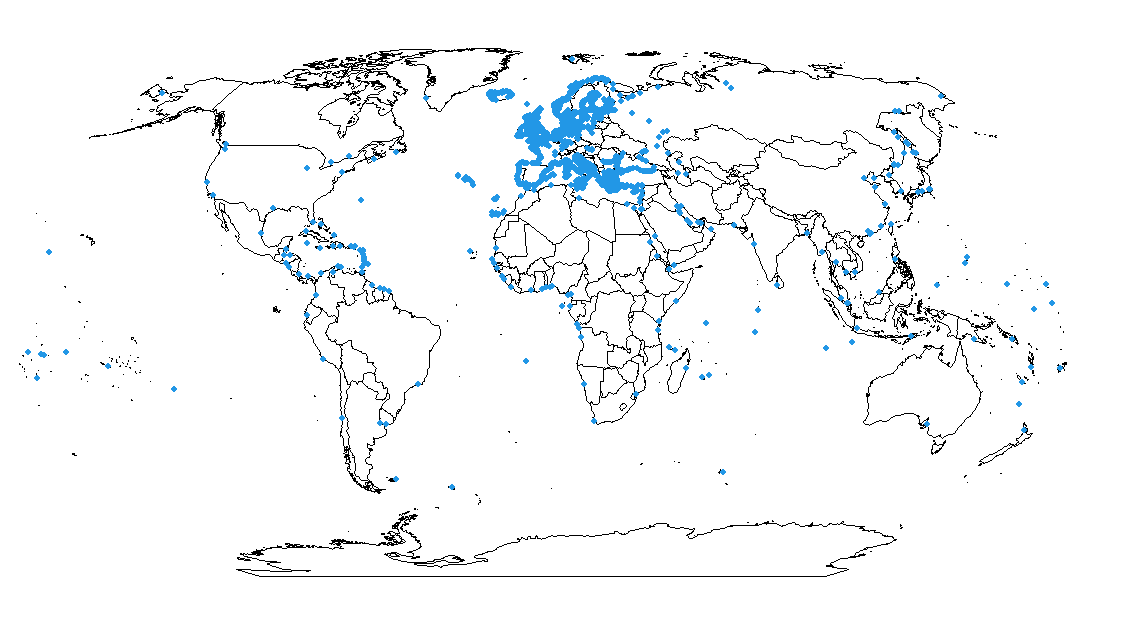

Figura 40.6: Localización de los puertos en el mapamundi (mismo CRS en los puertos y el mapa).

Nótese que en el paso de tres a dos dimensiones en el ejemplo de los puertos marítimos en el globo terráqueo, se ha utilizado la transformación o proyección Robinson. El lector podría preguntarse ¿por qué esa y no otra? ¿Es que no hay más? Hay muchas, pero la proyección adecuada, y en general el CRS adecuado, en cada caso depende de la localización y el rango espacial de los datos (pequeño-geográfico; grande-proyección). El paquete crsuggest (Walker, 2022) facilita la labor de elección de la proyección más conveniente, al sugerir transformaciones de sistemas de referencia de coordenadas adecuadas para conjuntos de datos espaciales. Devuelve un marco de datos con códigos CRS que se pueden utilizar para proyectos de transformación y mapeo CRS.

40.2.2 Formatos de datos espaciales

Como se avanzó anteriormente, en el ámbito del análisis espacial los datos espaciales pueden tener formato vector o formato raster, dependiendo de cómo sean los datos²⁶¹ (Lovelace et al., 2019). También se denominan datos vectoriales y raster o rasterizados (o mapas de bits).

Los datos vectoriales pueden representar tres tipos distintos de entidades: puntos, líneas y polígonos, y, quizás, su característica más importante es que cada punto, línea o polígono puede tener una tabla de atributos asociados. Los datos raster, en cambio, son una malla (en términos matemáticos, una matriz) donde cada celda (o píxel) tiene un tamaño similar y un valor específico. En el caso de las imágenes a color, el raster estaría compuesto por tres matrices sobrepuestas, cada una con celdas que tienen el valor correspondiente a un color primario. Cuando se utilizan imágenes de satélite u otros sensores cada archivo puede contener hasta cientos de matrices que representan distintos rangos de lo observado.

40.2.2.1 Datos de vectores

Este modelo de datos está basado en puntos georreferenciados. Los puntos, por ejemplo, representan localizaciones específicas. Un ejemplo es la localización de los hospitales y centros de salud de la ciudad de Toledo representados en la Fig. 40.7.

ggplot() +
  geom_sf(data = hosp_toledo, 
          aes(fill = "Hospitales y Centros Sanitarios"), 
          color = "blue") +
  labs(title = NULL, fill = NULL) +
  theme_minimal() +
  theme(legend.position = "right")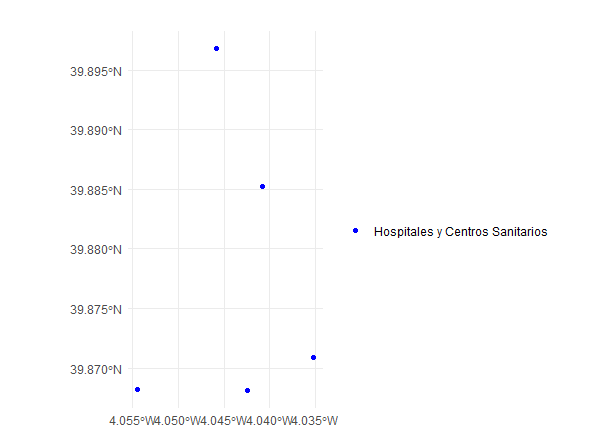

Figura 40.7: Hospitales y centros de salud en Toledo.

Los puntos también pueden estar conectados entre sí, de manera que formen geometrías más complejas, como líneas y polígonos. En la Fig. 40.8, el río Tajo está representado como una línea (tajo, sucesión de puntos unidos entre sí) y la ciudad de Toledo como un polígono (toledo, línea de puntos cerrada formando un espacio continuo).

ggplot(toledo) +
  geom_sf(fill = "cornsilk2") +
  geom_sf(data = tajo, col = "lightblue2", lwd = 2, alpha = 0.7) +
  geom_sf(data = hosp_toledo, col = "blue") +
  coord_sf(xlim = c(-4.2, -3.8), ylim = c(39.8, 39.95)) +
  theme_minimal()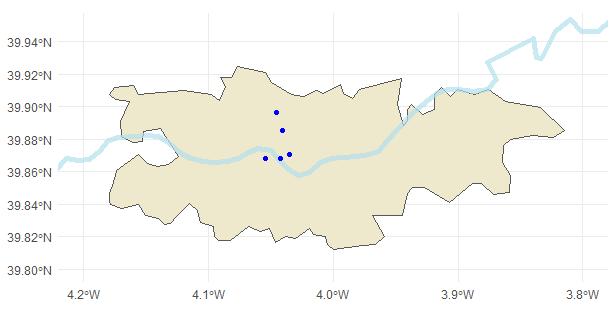

Figura 40.8: Datos vector: Puntos, líneas y polígonos.

Las extensiones más habituales de los archivos que contienen datos de vectores se muestran en la Tabla 40.1:

Tabla 40.1: Tipos de ficheros para datos vector
Tipo	Extensión
Shapefile	`.shp`, `.shx`, `.dbf`
GeoPackage vector	`.gpkg`
GeoJson	`.geojson`
GPX	`.gpx`
Geography Markup Language	`.gml`
Keyhole Markup Language	`.kml`
Otros	`.csv`, `.txt`, `xls`

Nota

ESRI Shapefile surgió como uno de los primeros formatos de intercambio de datos geográficos y en la actualidad es, quizá, el formato más empleado. Sin embargo, tiene una serie de limitaciones: es un formato multiarchivo y el CRS es opcional.

40.2.2.2 Datos raster

Los datos raster son datos proporcionados en una rejilla de píxeles (regulares o no) denominada matriz. El caso más popular de un raster es una fotografía, donde la imagen se representa como una serie de celdas, determinadas por la resolución de la imagen, es decir, el tamaño del píxel (por ejemplo, 5 $\times$ 5 unidades, si es regular, 5 $\times$ 10 unidades, si es irregular) y el valor del píxel (RGB –red, green, blue–, por ejemplo) que determina el color que presenta cada uno de estos píxeles. En el ámbito de los datos espaciales, un archivo raster está formado por una malla de píxeles georreferenciada, tal y como muestra la Fig. 40.9. En ella se visualiza el conjunto de datos elev incluido en el paquete CDR, que contiene los datos de altitud de la provincia de Toledo en metros.

library("terra")
elev <- rast(system.file("external/Toledo_DEM.asc", package = "CDR"))
plot(elev, main = " ")
pols <- as.polygons(elev, dissolve=FALSE)
plot(pols, add = TRUE, border = "grey90")
plot(st_geometry(Tol_prov), add = TRUE)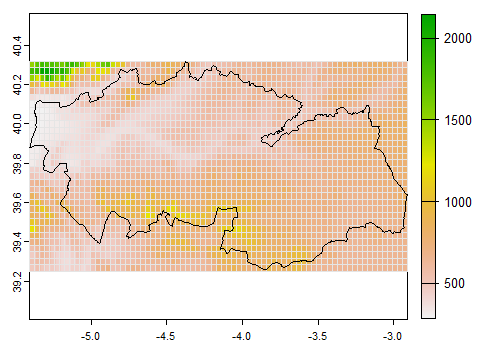

Figura 40.9: Datos $raster$. Altitud de la provincia de Toledo.

En la Fig. 40.9 el objeto raster elev tiene únicamente una capa. Eso implica que cada píxel tiene asociado un único valor, en este caso, la altitud media del terreno observado; pero podría tener más.

Las extensiones más habituales de los archivos que contienen datos raster se muestran en la Tabla 40.2.

Tabla 40.2: Tipos de ficheros para datos $raster$
Tipo	Extensión
ASCII Grid	`.asc`
GeoTIFF	`.tif`, `.tiff`
Enhanced Compression Wavelet	`.ecw`

40.3 Mi primer mapa

Definidos los elementos clave de los datos espaciales, a continuación se lleva a cabo un primer mapa, el resultado esperado cuando se trabaja con datos espaciales. Concretamente, se representa la distribución de la renta neta per cápita (renta_municipio_data) por municipio (municipios) en España en el año 2019.²⁶² Los datos están incluidos en el paquete CDR.

La integración de conjuntos de datos es una de las tareas iniciales al llevar a cabo un análisis de datos (véase Cap. 8). En el caso de la representación de la renta neta per cápita a escala municipal, los ficheros que hay que integrar son renta_municipio-data y municipios, los cuales deben tener, al menos, un campo en común, en este caso codigo_ine, para poder proceder a su unión. El siguiente código muestra cómo realizar esta unión con la función left_join().

library("CDR")
library("sf")
munis_renta <- municipios |>
  left_join(renta_municipio_data) |>   # une datasets
  select(name, cpro, cmun, `2019`)     # selecciona variables
#> Joining, by = "codigo_ine"

El siguiente paso es la representación gráfica de estos datos en el mapa. En la chunk se muestra como llevar a cabo dicha representación con la función ggplot().

ggplot(munis_renta) +
  geom_sf(aes(fill = `2019`), color = NA) +
  scale_fill_continuous(
    labels = scales::label_number(
      big.mark = ".", decimal.mark = ",", suffix = " €" )) +
  theme_minimal()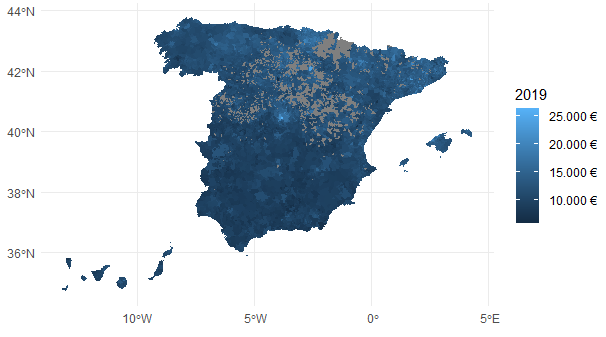

Figura 40.10: Renta neta media por persona (€) a escala municipal en España en 2019.

La Fig. 40.10 muestra un mapa temático de coropletas,²⁶³ es decir, una visualización sencilla de cómo varía la distribución de una variable (en este caso la renta neta media por persona) en una área geográfica (España). En la información contenida en el objeto munis_renta pueden verse una serie de elementos gráficos característicos de los objetos espaciales: los datos son de tipo vector, el tipo de geometría es MULTIPOLYGON, el CRS es ETRS89 y una leyenda explica el significado de la variable.

head(munis_renta)[1:3, ]
#> Simple feature collection with 3 features and 4 fields
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: -3.140179 ymin: 36.73817 xmax: -2.741701 ymax: 37.24562
#> Geodetic CRS: ETRS89
#> name cpro cmun 2019 geom
#> 1 Abla 04 001 10192 MULTIPOLYGON (((-2.775594 3...
#> Abrucena   04  002 10021 MULTIPOLYGON (((-2.787566 3...
#> Adra   04  003  8192 MULTIPOLYGON (((-3.051988 3...

40.4 Cómo (no) mentir con la visualización

Si se construye un mapa de coropletas como el de la Fig. 40.10, puede que la información aparezca distorsionada. Por ello, en aras de una correcta visualización de los datos que favorezca una interpretación realista de los mismos, es necesario tomar una serie de decisiones, entre las cuales están las relativas a:

el número de intervalos (o el establecimiento de los cortes o límites de tales intervalos) en caso de que haya que recurrir a una distribución por intervalos;
la escala de color a utilizar;
el tratamiento de los valores perdidos.

Recuérdese que los mapas de coropletas muestran la distribución espacial de una variable cuyos valores se dividen en clases o intervalos a los cuales se les aplica un esquema de colores, también llamado paleta, de tal manera que a cada clase le corresponde un color de la paleta. Aunque hay muchas formas en las que se pueden agrupar los valores de una variable en clases, el método de Fisher-Jenks es el más popular en los mapas temáticos y en especial, en los de coropletas.

Nota

El método de agrupación de datos de Fisher-Jenks utiliza un algoritmo no lineal para agrupar observaciones de modo que se maximice la homogeneidad dentro del grupo y la heterogeneidad entre los mismos. Este algoritmo está desarrollado específicamente para la clasificación de datos espaciales y su visualización en mapas (Slocum et al., 2022).

A la luz de las consideraciones anteriores, en el ejemplo que nos ocupa, cabe plantear una serie de preguntas:

¿Es necesario discretizar la variable? En caso afirmativo, ¿cómo se lleva a cabo tal discretetización? Si el objetivo es mostrar patrones espaciales de la variable, para una mejor representación, será necesario dividir los datos en clases. Una buena opción para llevar a cabo esta discretización es el paquete classInt (Bivand, 2020) y, concretamente, la función classIntervals(). De entre las distintas posibilidades que ofrece classInt::classIntervals() se utiliza el método de Fisher-Jenks.
¿Cuál es la escala de color adecuada? Las decisiones sobre los colores son cruciales para hacer un mapa visualmente efectivo. En este caso se ha elegido la paleta de color inferno.
¿Son necesarias más transformaciones? Sí. En este caso se eliminan los municipios sin datos (sombreados en color gris).

El mapa de la Fig. 40.11 proporciona ahora una visualización adecuada de la renta neta per cápita en España, a escala municipal, en 2019.

munis_renta_clean <- munis_renta |>
  filter(!is.na(`2019`))

# crea Fisher-Jenks clases
library(classInt)
fisher <- classIntervals(munis_renta_clean$`2019`,
style = "fisher", n = 10
)

ggplot(munis_renta_clean) +
  geom_sf(aes(fill = cut(`2019`, fisher$brks)), color = NA) +
            scale_fill_viridis_d(option= "A" , 
                                 labels= scales::label_number(suffix= "€")) +
guides(fill = guide_colorsteps()) +
  labs(fill= "Fisher-Jenks") +
theme_minimal()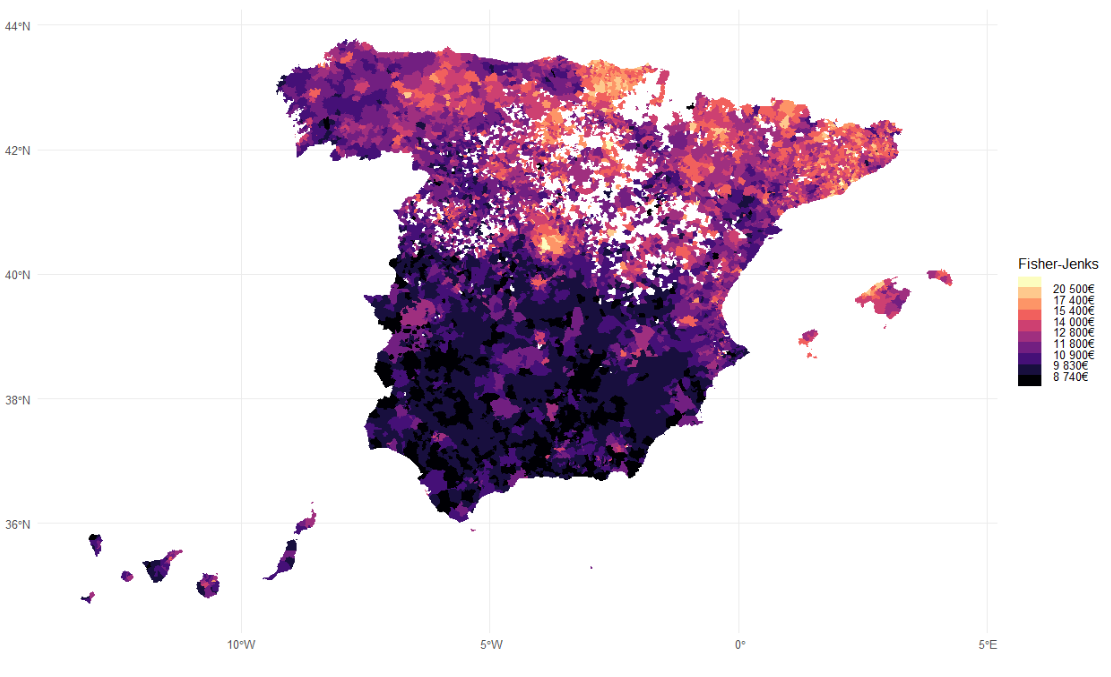

Figura 40.11: Renta neta per cápita en España, a escala municipal, en 2019, con Fisher-Jenks.

40.5 Mapas espaciotemporales

La dimensión temporal cobra cada vez más relevancia en el ámbito espacial, y por ello es importante representar en el tiempo los procesos espaciales.²⁶⁴ A modo de ejemplo, la Fig. 40.13 representa la temperatura mínima registrada en España del 6 al 10 de enero de 2021, CDR::tempmin_data, durante la Borrasca Filomena. Al igual que en ejemplo anterior, para la representación se dispone de dos ficheros tempmin_data, con los datos de temperatura y esp, un objeto R que se crea con mapSpain::esp_get_ccaa().

tmin_sf <- st_as_sf(tempmin_data, 
  coords = c("longitud", "latitud"),
  crs = 4326) # coordenadas geográficas longitud/latitud WGS84

esp <- esp_get_ccaa() |> # sf objeto, contorno de España
        filter(ine.ccaa.name != "Canarias") # excluye Canarias

Recuérdese que la primera pregunta que se debe formular es: ¿el CRS de las estaciones de medición de la temperatura está en la misma proyección que el contorno de España?

st_crs(tmin_sf) == st_crs(esp)
#> [1] FALSE
esp2 <- st_transform(esp, st_crs(tmin_sf))
st_crs(tmin_sf) == st_crs(esp2)
#> [1] TRUE

Comprobado el CRS, es habitual representar las coordenadas con las que se trabaja. La Fig. 40.12 muestra la localización de las estaciones que registran la temperatura en España.

ggplot(esp2) +
  geom_sf() +   
  geom_sf(data = tmin_sf)

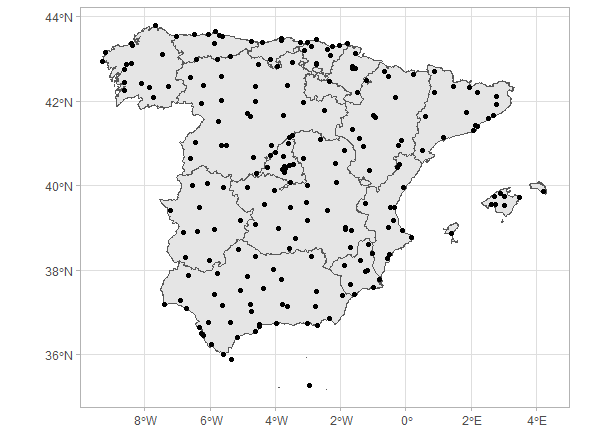
Figura 40.12: Estaciones de la AEMET en la Península Ibérica.

Por último, se representa el mapa espaciotemporal con la función ggplot(), indicando en el argumento facet_wrap() la dimensión temporal.

Nota

Los paquetes tmap (Tennekes, 2018) y mapsf (Giraud, 2022) son referentes en la construcción de mapas temáticos y pueden utilizarse como alternativa.

# definición de intervalos
cortes <- c(-Inf, seq(-20, 20, 2.5), Inf)
colores <- hcl.colors(15, "PuOr", rev = TRUE)

tmin_sf_sptem <- tmin_sf |>
  arrange(fecha, desc(tmin))

ggplot() +
  geom_sf(data = esp2, fill = "grey95") +
  geom_sf(data = tmin_sf, aes(color = tmin), size=3, alpha= .7) +
  facet_wrap(vars(fecha),ncol = 3) + 
  labs(color = "Temp. mím") +
  scale_color_gradientn(
    colours = colores,
    breaks = cortes,
    labels = ~str_c(. , "º"),
    guide = "legend") +
    theme_light()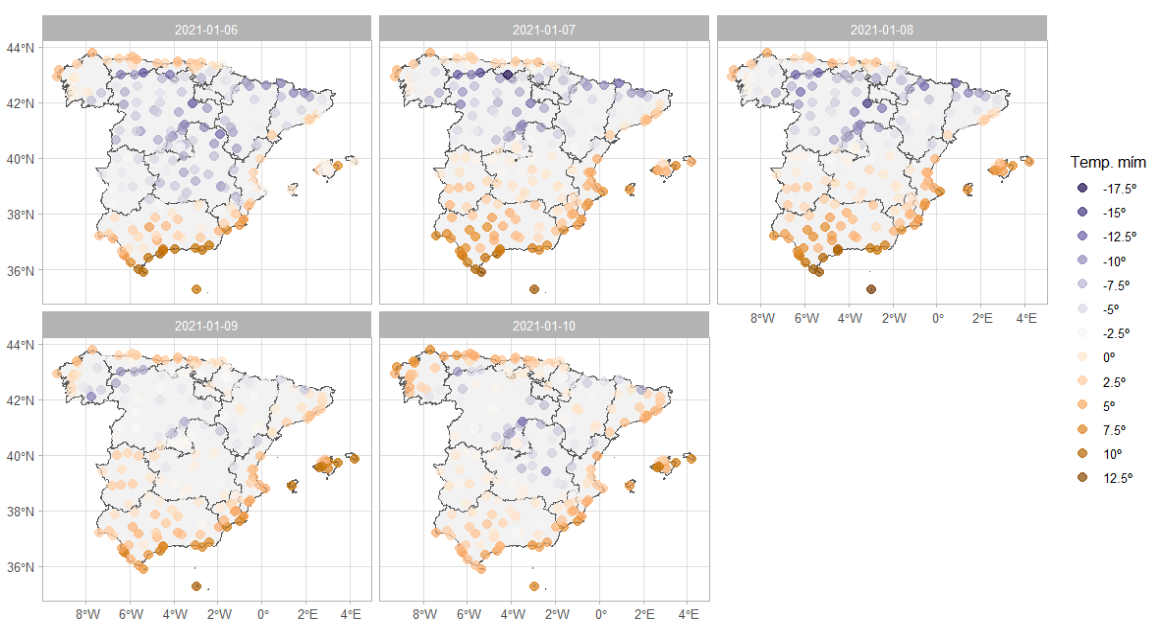

Figura 40.13: Temperatura mínima en España (6-10 enero 2021).

40.6 Mapas interactivos

El desarrollo de la informática ha propiciado también el desarrollo de la geocomputación, que está relacionada con los desarrollos webs y permite, entre otras cosas, la representación de mapas interactivos.

A modo de ejemplo, en la Fig. 40.14 se representa la versión interactiva del mapa de la Fig. 40.1. Para ello se utiliza la librería leaflet. Estos mapas dinámicos, ampliables y desplazables son más informativos que los mapas estáticos y, además, constituyen una alternativa que puede proporcionar al usuario una experiencia diferente, además de una mayor interacción.

library("leaflet")
library("isdas")
data("snow_deaths")
data("snow_pumps")

## crea mapa interactivo
snow_map <- leaflet() |>
  setView(lng = -0.136, lat = 51.513, zoom = 16) |>
  addTiles() |>
  addMarkers( data = snow_deaths, ~long, ~lat,
    clusterOptions = markerClusterOptions(),
    group = "Deaths" ) |>
  addMarkers(data = snow_pumps, ~long, ~lat,
    group = "Pumps" )

snow_map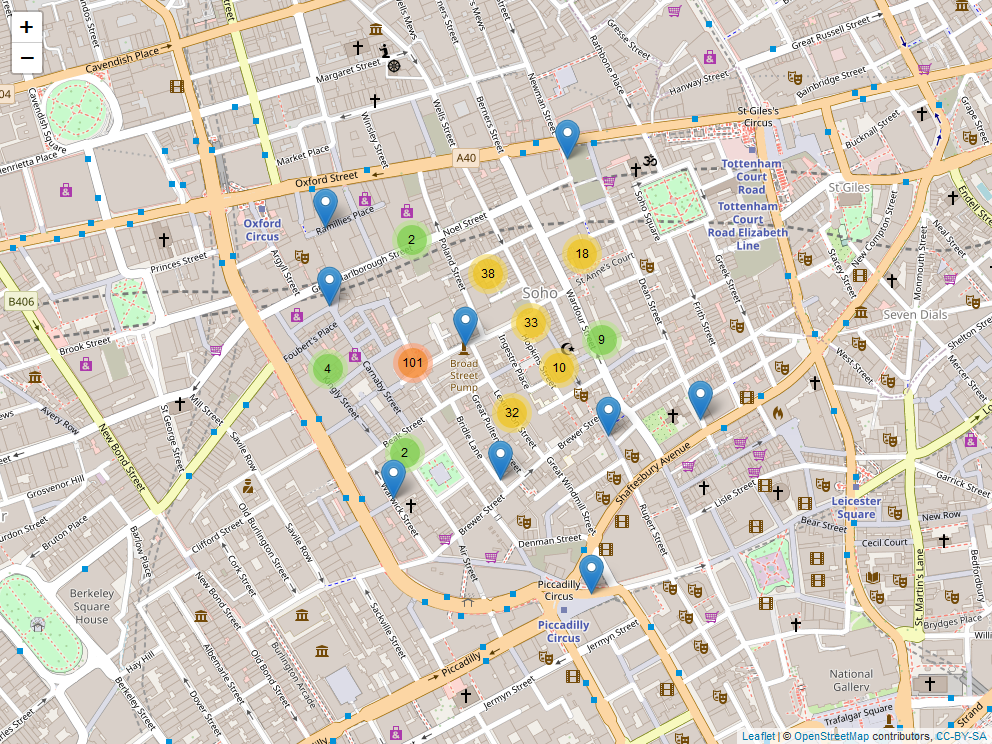

Figura 40.14: Mapa interactivo de las muertes por cólera en barrio del Soho (Londres) según Snow en 1854.

Resumen

Los datos espaciales son aquellos que contienen información de una zona geográfica de la Tierra. Vienen definidos por coordenadas y por un sistema de referencia de coordenadas que debe tenerse en cuenta para su representación.
Los datos espaciales pueden venir dados en dos tipos de formato: vector y raster.
Los datos espaciales pueden clasificarse en: geoestadísticos, reticulares y puntuales.

39 Análisis de grafos y redes sociales

41 Geoestadística