Capítulo 49 Optimización de inversiones publicitarias

Carlos Real Ugena

Deloitte

49.1 Metodologías para optimizar las inversiones publicitarias

Uno de los principales retos a los que se enfrentan los departamentos de marketing de cualquier compañía es cuantificar el impacto de la publicidad en el negocio. Esta medición es clave en la optimización de las inversiones que destinan a cada medio publicitario, existiendo múltiples métodos para medir el ROI (return on investment), es decir, el retorno que se obtiene por cada euro invertido en publicidad. Antes de revisar un ejemplo práctico, es necesario entender bien las características que presentan cada uno de ellos. Los métodos de cuantificación del impacto de la publicidad en el negocio, según la investigación llevada a cabo por la consultora Gartner,²⁹¹ se pueden clasificar en cuatro grandes grupos:

Marketing Mix Modeling (MMM): modelos de series temporales que sirven para estimar la contribución del marketing u otras variables explicativas a las ventas desde un punto de vista estratégico.
Multitouch Attribution (MTA): modelos de atribución que valoran cada punto de contacto (touchpoint) del recorrido del cliente (customer journey), asignando a cada uno un peso en la conversión (venta, descarga de folleto, etc). Son modelos tácticos que normalmente se centran en el canal online.
Holdout Testing of Experiments (EXP): modelos causales que evalúan el impacto de una campaña publicitaria a partir de una muestra de control y otra de test.
Unified Measurement Approaches (UMA): combinación de los modelos anteriores (MMM + MTA + EXP) con el objetivo de tener una visión unificada de los resultados.

En la comparativa que se muestra en la Fig. 49.1 se resume el objetivo de cada uno de los modelos, así como las preguntas que permiten responder:

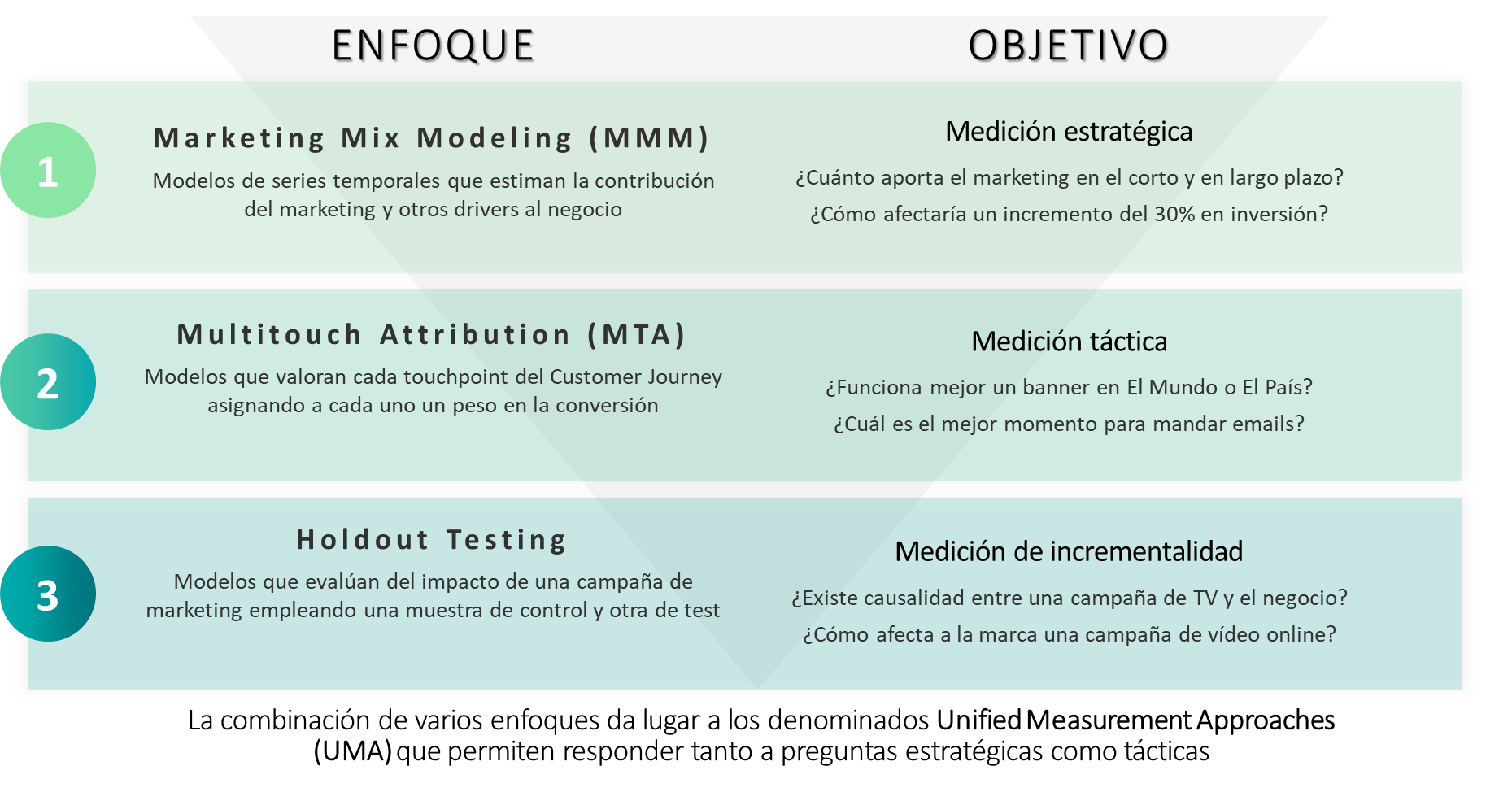
Figura 49.1: Comparativa de metodologías de medición.

En los últimos años se han producido una serie de cambios en el entorno de la industria del marketing digital enfocados a garantizar el más estricto control de la privacidad de los usuarios. Desde el lanzamiento de la nueva ley de protección de datos (GDPR), en 2018, hasta la reciente confirmación por parte de Google de la prohibición de uso de cookies de terceros en Chrome, la posibilidad de acceder a datos de identificación personal para la medición y optimización del impacto de las campañas de publicidad digital está cada vez más limitada.

Esta situación está provocando que el primer tipo de enfoque, el MMM, esté siendo el gran beneficiado, dado que es una técnica que no depende del acceso a datos a nivel de individuo. El ejemplo más claro sobre el protagonismo que está alcanzando el MMM es que grandes compañías como Meta, Google y Uber están desarrollando soluciones open source basadas en técnicas de machine learning que integran grandes avances y mejoras sobre las metodologías tradicionales. Entre las metodologías que han desarrollado hay claras diferencias en las bases teóricas sobre las que se rigen, así como diferencias en tiempos de computación, lenguaje en el que se han desarrollado o capacidades funcionales. A continuación se detallan las principales características de cada una de ellas:

• Robyn:²⁹² desarrollado por Meta (Facebook Marketing Science, 2021) y pensado para datasets con gran cantidad de variables independientes dado que trabaja con regresiones ridge (cubiertas en el Cap. 19), las cuales están pensadas para lidiar con problemas de multicolinealidad, muy presentes en este tipo de análisis. Cabe destacar que, entre las pruebas que realiza, ofrece una serie de outputs visuales avanzados que permiten al usuario seleccionar el que mejor se adapta al contexto de negocio y necesidad. Requiere tiempos de cómputo alto, pudiendo llegar hasta las tres horas, y permite hacer optimizaciones de presupuesto.

• Lightweight:²⁹³ desarrollado por Google, sus fundamentos teóricos se basan en modelos bayesianos. La particularidad de esta solución es la posibilidad de incluir datos geográficos para su posterior segregación. Lightweight también considera distintos tipos de adstock (recuerdo publicitario), así como la tendencia y estacionalidad de la serie a explicar. El uso de esta herramienta es más sencillo, aunque los resultados se exponen en un notebook y no posee outputs más elaborados como el resto de soluciones. Por último, también permite realizar optimizaciones de presupuesto.

• Orbit:²⁹⁴ desarrollado por Uber, se basa en modelos bayesianos. Permite al usuario medir los retornos a lo largo del tiempo, lo cual hace que sea un modelo adecuado para compañías con grandes picos de ventas. Incluye análisis de estacionalidad mediante la descomposición de la serie en series de Fourier. Es el modelo más complejo de desarrollar; sin embargo, el tiempo de ejecución es bajo. Cabe destacar que es la librería más estable y, por lo tanto, se podría utilizar para realizar reportes con mayor frecuencia. No incluye la posibilidad de optimizar presupuestos.

49.2 Robyn como alternativa open source en R

Robyn está ganando en popularidad debido a las continuas mejoras que se están aplicando desde Meta, así como gracias a su adaptabilidad a la realidad del anunciante. Además, existe un paquete en R validado y subido al CRAN que lo sitúa como una gran alternativa de código abierto en R para iniciarse en el campo de la medición y optimización del retorno de las inversiones publicitarias. La ecuación empleada es la siguiente: \[\begin{equation} y_t= \beta_0 + Scurve(x_j) + \beta_{hol} hol_t + \beta_{sea} sea_t + \beta_{trend} trend_t + ... + \beta_{ETC} ETC_t + \epsilon_t \end{equation}\] donde:

\[\begin{equation} \begin{aligned} y_t &= \text{ventas en el instante} \,t, \\ t &= \text{instante de las variables (por ejemplo, semanas)}, \\ j &= \text{subíndice del medio (por ejemplo, TV o Display)}, \\ \beta_0 &= \text{intercepto}, \\ Scurve(x,j) &= \beta_j \times \frac{x_{decay_{ t,j}}^\alpha}{x_{decay_{ t,j}}^\alpha + \gamma^\alpha} \, \text{transformación no lineal de curva en S}, \\ \alpha,\gamma &= \text{hiperparámetros que definen la $S$ $curve$}, \\ x_{decay_{t,j}} &= x_{t,j} + \theta_j x_{decay_{ t,j-1}} \hspace{0,1cm}(adstock, \text{es decir, el recuerdo publicitario)}, \\ x_j &= \text{inversión publicitaria en cada medio}\,j, \\ \theta_j &= \text{tasa fija de decrecimiento en cada medio}\,j, \\ \gamma &: \text{implementada en la $S$ $curve$, donde} \,\gamma_{tran} = cuantil(x_{decay_j}, \gamma), \\ \beta_j &= \text{coeficientes de cada medio}\,j, \\ hol &=\, \text{festivos}, \\ sea &=\, \text{estacionalidad}, \\ tren d&=\, \text{tendencia}, \\ ETC &=\, \text{resto de variables independientes (precio, promociones, etc)}, \\ \epsilon_t &= \text{término de error en el instante} \,t. \\ \end{aligned} \end{equation}\]

Las variables de medios no suelen presentar un efecto lineal sobre la variable de negocio que se modeliza, sino que la publicidad tiende a presentar rendimientos decrecientes no lineales. Para modelizar este efecto se utiliza la función biparamétrica de S curve o curva de rendimientos decrecientes. Esta curva permite optimizar los repartos presupuestarios en todos los canales de medios, ya que su forma en “S” indica tanto el umbral a partir del cual los resultados del gasto presupuestario mejoran significativamente el objetivo (por ejemplo, ventas) como en qué punto está saturando y, por lo tanto, perdiendo eficacia.

A continuación, se aplica Robyn sobre un ejemplo con información simulada del sector hotelero, donde el objetivo es predecir el número de reservas de un hotel en función de una serie de predictores (entre ellos, las inversiones publicitarias). Toda la información sobre cómo aplicar esta metodología se puede consultar en GitHub.²⁹⁵ La versión utilizada en este ejemplo práctico es la 3.6.3, disponible en el CRAN o descargable desde GitHub.²⁹⁶ Este ejercicio traza el camino más corto que se puede seguir hasta llegar a los principales outputs y a la interpretación de los mismos. Sin embargo, para conocer en detalle la metodología, se recomienda seguir profundizando a través de la realización de pruebas adicionales más complejas.

Para comenzar, se carga el paquete Robyn, comprobando que se está trabajando con la versión 3.6.4 y forzando el uso de multicore al utilizar RStudio:

library("Robyn") 
packageVersion("Robyn")
Sys.setenv(R_FUTURE_FORK_ENABLE = "true")
options(future.fork.enable = TRUE)

Se carga una librería de Python llamada nevergrad (Facebook Research AI, 2019), necesaria en el proceso de estimación de los hiperparámetros, invocándola desde R. Hay varias opciones para llevar a cabo este proceso. Una de ellas es instalar primero el paquete reticulate (Ushey et al., 2022) y, a continuación, nevergrad vía pip:

# install.packages("reticulate")
library("reticulate")
virtualenv_create("r-reticulate")
use_virtualenv("r-reticulate", required = TRUE)
py_install("nevergrad", pip = TRUE)
py_config()

En caso de encontrar alguna dificultad al cargar nevergrad, existen distintas alternativas para su instalación que se pueden consultar en GitHub.²⁹⁷

Posteriormente, se carga la tabla que recoge la información simulada del sector hotelero con la que se medirá el impacto de la publicidad:

library("CDR")
data("hotel_tablonsemanal")
head(hotel_tablonsemanal)

Se detalla a continuación la información que contiene cada variable:

semana: lunes de la semana de referencia.
reservas: número de reservas que ha conseguido la cadena hotelera en cada una de las semanas bajo análisis.
turismo: número de pernoctaciones.
covid_mov: movilidad desde el comienzo de la pandemia.
notoriedad: conocimiento espontáneo de la marca a lo largo del tiempo.
temperatura: temperatura media.
tv_grps20 y tv_inv: métrica de impactos (los GRP) e inversión realizada en TV.
resto_off_inv: resto de inversiones offline realizadas.
paidsearch_imp y paidsearch_inv: métrica de impactos (impresiones) e inversión realizada en Paid Search.
display_imp y display_inv: métrica de impactos (impresiones) e inversión realizada en Display.
onlinevideo_imp y onlinevideo_inv: métrica de impactos (impresiones) e inversión realizada en Online Video.
competidores: inversión realizada por la competencia.
eventos: recoge eventos que tienen impacto en la serie de reservas. En este caso se considera el Black Friday.

El objetivo de este ejercicio es estimar el impacto de cada una de las variables detalladas sobre las reservas, poniendo especial atención en las variables de medios —TV, Resto Medios Offline, Paid Search, Display y Online Video— para medir sus efectos y, posteriormente, optimizar las inversiones en ellos.

Con este fin, se cargan los festivos a partir de una tabla auxiliar:

data("festivos")
head(festivos)

Se fija dónde se guardarán los resultados:

robyn_object <- "data/MyRobyn.RDS"
ruta_outputs <- "data"

Y se define la configuración inicial del modelo:

hotel_tablonsemanal$eventos <- hotel_tablonsemanal$eventos |> replace_na('na')
InputCollect <- robyn_inputs(
    dt_input = hotel_tablonsemanal,
    dt_holidays = festivos,
    date_var = "semana", # tiene que tener este formato "2020-01-01"
    dep_var = "reservas", # solo una variable dependiente
    dep_var_type = "conversion", # "revenue" o "conversion". En nuestro caso son reservas.
    prophet_vars = c("trend", "season", "holiday"), # "trend=tendencia","season=estacionalidad", "weekday=dia de la semana" & "holiday=festivos"
    prophet_signs = c("default", "default", "default"),
    prophet_country = "ES", # seleccione un país. España en nuestro caso
    context_vars = c("eventos", "turismo", "covid_mov", "notoriedad", 
                     "temperatura", "competidores"), # variables de contexto que no sean medios
    context_signs = c("default", "positive", "negative", 
                      "positive", "default", "negative"), # signos fijados a priori (por ejemplo, el turismo debe tener un signo positivo puesto que estamos analizando reservas de hotel)
    paid_media_spends = c("display_inv","onlinevideo_inv",  "paidsearch_inv",
                          "resto_off_inv", "tv_inv"), # variables de inversión
    paid_media_signs = c("positive", "positive", "positive", "positive", "positive"),
    paid_media_vars = c("display_imp", "onlinevideo_imp",   
                        "paidsearch_imp"    ,"resto_off_inv" ,"tv_grps20"), # variables de impacto si están disponibles. Si no están disponibles utilice el coste como en el caso de Resto_off_inversion
    factor_vars = c("eventos") # especifique variables que son factores. En nuestro caso, solo la variable de Eventos
    window_start = "2018-10-01", #fecha de inicio del modelo. En nuestro caso, octubre 2010 porque previamente no se tienen datos de reservas
    window_end = "2021-09-27", #fecha fin del modelo
    adstock = "geometric" # tipo de adstock. Seleccione el adstock geométrico para reducir tiempos de cómputo
  )
print(InputCollect)

Después, se obtienen los nombres de los hiperparámetros a ajustar:

hyper_names(adstock = InputCollect$adstock, all_media = InputCollect$all_media)

A continuación, se definen los rangos en los que se moverán los hiperparámetros que definen la S curve de cada medio. En este ejemplo se utilizan los mismos límites para $\alpha$ y $\gamma$, que controlan la forma de la curva y el punto de inflexión, respectivamente. Por otro lado, $\theta$ define el adstock, que se puede acotar teniendo en cuenta los intervalos recomendados por Meta: TV (entre 0,3 y 0,8), Resto Medios Offline (entre 0,1 y 0,4) y Digital (entre 0 y 0,3). En este caso, se deja $\theta$ libre entre 0 y 0,99 para todos los medios:

hyperparameters <- list(
  display_inv_alphas = c(0.0001, 3),display_inv_gammas = c(0.3, 1),
  display_inv_thetas = c(0, 0.99), onlinevideo_inv_alphas = c(0.0001, 3),
  onlinevideo_inv_gammas = c(0.3, 1), onlinevideo_inv_thetas = c(0, 0.99),
  paidsearch_inv_alphas = c(0.0001, 3), paidsearch_inv_gammas = c(0.3, 1),
  paidsearch_inv_thetas = c(0, 0.99), resto_off_inv_alphas = c(0.0001, 3),
  resto_off_inv_gammas = c(0.3, 1), resto_off_inv_thetas = c(0, 0.99),
  tv_inv_alphas = c(0.0001, 3), tv_inv_gammas = c(0.3, 1),tv_inv_thetas = c(0, 0.99)
)

Se añaden los hiperparámetros al input para ajustar los modelos:

InputCollect <- robyn_inputs(InputCollect = InputCollect, 
                             hyperparameters = hyperparameters)
print(InputCollect)

y se ejecuta el modelo definiendo el número de iteraciones y trials. En este ejercicio, el número de iteraciones será 2.000 y el de trials, 10, obteniendo un total de 20.000 posibles soluciones del modelo:

OutputModels <- robyn_run(
  InputCollect = InputCollect, 
  iterations = 2000,
  trials = 10,
  outputs = FALSE # se desactivan los outputs que se guardarán después
)
print(OutputModels)

Los mejores resultados de la modelización según el frente de Pareto (conjunto de óptimos de Pareto que minimizan el error cuadrático medio normalizado –normalized root mean square error, NRMSE– y la descomposición de la suma cuadrática de la distancia²⁹⁸ –decomposition root sum of squared distance, DECOMP.RSSD–) se guardan en la carpeta seleccionada:

OutputCollect <- robyn_outputs(
  InputCollect, OutputModels,
  pareto_fronts = 3,
  csv_out = "all",
  clusters = TRUE,
  plot_pareto = TRUE,
  plot_folder = ruta_outputs #ruta para exportar los resultados
)
print(OutputCollect)

Para finalizar, se revisan los distintos modelos obtenidos y el resumen gráfico proporcionado por Robyn. Se recomienda profundizar en la interpretación de uno de los modelos obtenidos con buen ajuste. A través del one-pager (Fig. 49.2), se puede consultar toda la información relativa al impacto de la publicidad, incluyendo métricas relativas a la bondad del ajuste como el coeficiente de determinación o R2 y el NRMSE (panel superior izquierdo).

Figura 49.2: One-pager de resultados de Robyn.

Los principales outputs a evaluar de los modelos se visualizan en los gráficos del one-pager:

Descomposición en cascada de la repuesta por predictor (Response Decomposition Waterfall by Predictor): representa el peso de cada una de las variables en el modelo. En el ejemplo, el peso de la publicidad es del 54,5% (suma de los pesos de las variables de inversiones).
Respuesta real vs. estimada (Actual vs. Predicted Response): muestra el ajuste del modelo. En este caso, la línea del ajuste (azul) y la real (naranja) se aproximan bastante, indicando que el modelo es capaz de explicar la mayor parte de la variabilidad de la serie de reservas.
Cuota de gasto frente a cuota de efecto con coste por adqusisición (CPA) total (Share of Spend vs. Share of Effect with total CPA): muestra la relación entre la cuota de inversión y la cuota de contribución generada por las inversiones publicitarias. En este ejercicio, se puede observar que tanto Online Video como Display obtienen un aporte mayor de lo esperado por su cuota de inversión, lo que hace que el CPA (valores en azul) sea menor para estos medios. La TV se encuentra en el polo opuesto, con el máximo CPA, es decir, es el medio menos eficiente a la hora de generar reservas.
Curvas de respuesta y gastos medios por canal (Response Curves and Mean Spends by Channel): muestra la relación no lineal existente entre las inversiones y las reservas. Es el input principal a la hora de optimizar las inversiones.
Adstock geométrico: tasa constante de decrecimiento en el tiempo (Geometric Adstock: Fixed Decay Rate Over Time): muestra el efecto recuerdo (adstock) de cada medio publicitario. Se puede observar que los medios offline (TV y Resto Medios Offline) son aquellos que presentan un efecto recuerdo más prolongado. No se debe olvidar que la configuración del modelo permite fijar el rango de valores que puede tomar el adstock en cada uno de los medios.
Ajustados frente a residuos (Fitted vs. Residual): muestra la nube de puntos para los datos ajustados (eje x) y los residuos (eje y). Este gráfico debe mostrar que los puntos están aleatoriamente ubicados alrededor del eje horizontal.

Y, ¿cómo se pueden optimizar las inversiones en medios empleando estos resultados? En primer lugar, se pueden utilizar las curvas obtenidas (parámetros guardados en el fichero all_hyperparameters.csv) para simular distintos escenarios y seleccionar el que genere un mayor número de reservas. La segunda opción es utilizar la documentación de código²⁹⁹ incluida en el paso 5 para generar el reparto óptimo de inversión basado en un presupuesto preestablecido.

En este capítulo se dan los primeros pasos en la medición y optimización del ROI de las inversiones publicitarias. Se anima al lector a que siga profundizando en este campo tan apasionante y complejo para basar las decisiones futuras de inversión en análisis desarrollados en R.

48 Análisis de una red criminal

50 ¿Cómo tuitea Elon Musk?