Skip to main content

Fundamentos de ciencia de datos con R

Capítulo 28 Métodos ensamblados: \(\bf \textit {bagging}\) y \(\bf \textit{random}\) \(\bf \textit{forest}\)

Ramón A. Carrasco\(^{a}\), Itzcóatl Bueno\(^{a,\hspace{0,05cm}b}\) y José-María Montero\(^{c}\)

\(^{a}\)Universidad Complutense de Madrid
\(^{b}\)Instituto Nacional de Estadística
\(^{c}\)Universidad de Castilla-La Mancha

28.1 Introducción a los métodos ensamblados

Puede ocurrir que ninguno de los algoritmos hasta ahora presentados (Caps. 24, 25, 26 y 27) proporcionen resultados convincentes para el problema que se quiere modelar. El aprendizaje ensamblado (Zhou, 2012) es un paradigma que, como muestra la Fig. 28.1, en lugar de entrenar un modelo que proporcione resultados muy precisos, entrena un gran número de modelos no tan precisos y después combina sus predicciones para obtener un metamodelo con una precisión superior.

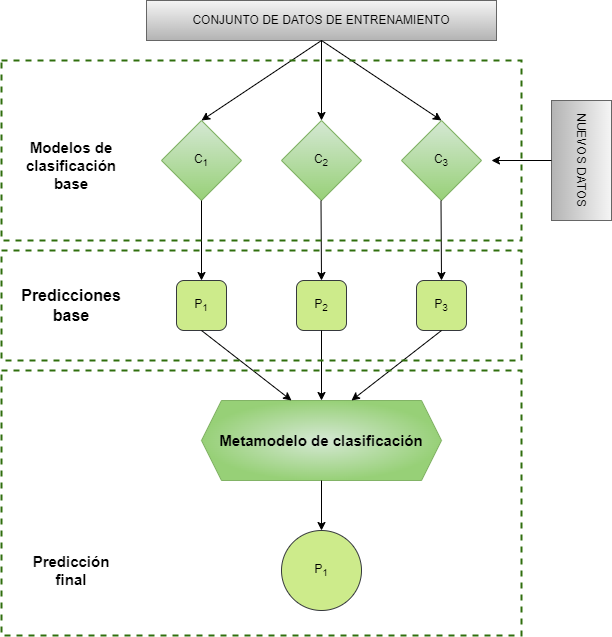
Esquema de un metamodelo.

Figura 28.1: Esquema de un metamodelo.

A los modelos que se combinan se les suele denominar algoritmos “débiles” (con menor capacidad de aprender patrones complejos en los datos) y, generalmente, son rápidos tanto en tiempo de entrenamiento como de procesamiento. Existen dos paradigmas de aprendizaje ensamblado: bagging y boosting (Cap. 29).

28.2 \(\bf \textit{Bagging}\)

Bagging es una técnica para reducir la varianza dentro de un conjunto de datos con “ruido”. En bagging, se construyen múltiples árboles de decisión en cada uno de los cuales se utiliza una muestra aleatoria aleatoria con remplazamiento de los datos del conjunto de entrenamiento. Dichos modelos (débiles) se entrenan por separado y finalmente se combinan las predicciones de cada uno de ellos, calculando la media de dichas predicciones (en el caso de regresión) o mediante un sistema de votación (en el caso de un problema de clasificación)198. El resultado de esta combinación de modelos débiles es una ganancia en la precisión o el sesgo de las predicciones.

Nótese que el algoritmo de un árbol de decisión no podado puede ser propenso a sobreajustarse (alta varianza y bajo sesgo) y que si es muy pequeño es propenso al subajuste (varianza pequeña y sesgo elevado). La combinación de árboles de decisión evita estas situaciones y busca el equilibrio varianza-sesgo, que permitirá mejores generalizaciones a nuevos conjuntos de datos.

La principal característica del bagging es el muestreo bootstrap (véanse Caps. 10 y 14). Una muestra bootstrap es una muestra aleatoria de los datos tomados con reemplazamiento (Efron & Tibshirani, 1986). Esto significa que, después de seleccionar una observación (una instancia) del conjunto de datos de entrenamiento para incluirla en la muestra, aún queda disponible para una selección posterior. Una muestra bootstrap tiene el mismo tamaño que el conjunto de datos original a partir del cual se construyó.

En el bagging, el objetivo de este remuestreo es que cada árbol esté entrenado con una muestra específica para él, y por tanto, los distintos árboles generen respuestas únicas, esto es, modelos débiles distintos. Aunque esta manera de proceder no elimina la problemática del sobreajuste, los patrones presentes en el conjunto de datos aparecerán en la mayoría de los árboles entrenados y, por tanto, en la predicción final. Es por ello que el bagging es una técnica de gran eficacia para el tratamiento de los valores atípicos y para la reducción de la varianza, que generalmente afecta a un modelo compuesto por un único árbol de decisión.

28.2.1 Procedimiento con R: la función bagging()

Para entrenar un modelo bagging se utiliza la función bagging() del paquete ipred de R.

bagging(formula, data, ...)
  • formula: \(Y \sim X_1 + ... + X_p\) indica cuál es la variable independiente y cuáles las predictivas. El signo “+” indica “conjunto de” y no debe confundirse con la existencia de una relación lineal entre la variable respuesta y las predictoras (que pudiera existir o no).
  • data: conjunto de datos con el que se entrena el modelo.
  • nbagg: número de replicaciones bootstrap.
  • coob: indica si se debe calcular una estimación de la ratio de error de predicción.

28.2.2 Implementando bagging en R

Igual que en los capítulos anteriores, para ilustrar el algoritmo bagging se retoma el ejemplo de la compra de un tensiómetro digital por parte de los clientes de una empresa. Los datos sobre compras de clientes y el importe gastado en dichas compras se encuentran en el conjunto de datos dp_entr del paquete CDR. El objetivo es clasificar a los clientes de la empresa en dos grupos: los que comprarían el tensiómetro digital y los que no. Aunque se utiliza la función bagging(), ya mencionada en la Sec. 28.2.1, se pueden utilizar otras muchas funciones.

# se fija la semilla aleatoria
set.seed(101)

# Se entrena el modelo
bag_model <- bagging(
  formula = CLS_PRO_pro13 ~ .,
  data = dp_entr,
  nbagg = 100,  
  coob = TRUE,
  control = rpart.control(minsplit = 2, cp = 0)
)
# se muestra la salida del modelo
bag_model

Bagging classification trees with 100 bootstrap replications 

Call: bagging.data.frame(formula = CLS_PRO_pro13 ~ ., data = dp_entr, 
    nbagg = 100, coob = TRUE, control = rpart.control(minsplit = 2, 
        cp = 0))

Out-of-bag estimate of misclassification error:  0.1416

Como puede observarse en los resultados anteriores, el número de muestras bootstrap es de 100; en otros términos, se entrenan, independientemente, 100 modelos débiles. El metamodelo, o modelo fuerte, generado mediante la combinación de los 100 modelos débiles proporciona un porcentaje de clasificación errónea del 14,16%. Desafortunadamente, la función bagging() no selecciona el número óptimo de replicaciones para hacer mínimo el porcentaje de clasificación errónea. Para seleccionar el número de replicaciones que minimice dicho porcentaje, se puede graficar la curva de porcentaje de clasificación errónea vs. el número de replicaciones (nbagg), como en la Fig. 28.2. Si se itera el modelo variando los valores del hiperparámetro nbagg (en este ejemplo entre 10 y 150, incrementándose de cinco en cinco), se observa que el mínimo porcentaje de clasificación errónea (13,79%) se obtiene con 60 replicaciones.

missclass <- c() # vector vacío para recopilar el error en cada iteración
for (n in seq(10,150,5)) { # valores a probar para nbagg
  # se establece la semilla aleatoria
  set.seed(101)
  # se entrena el modelo
  bag_model <- bagging(
  formula = CLS_PRO_pro13 ~ .,
  data = dp_entr,
  nbagg = n,  
  coob = TRUE,
  control = rpart.control(minsplit = 2, cp = 0)
  )
  # se agrega el error de esta iteración
  missclass <- c(missclass, bag_model$err) # se agrega el error de esta iteración
}
plot(seq(10,150,5),missclass,type = "l",xlab = "Número de árboles", ylab="Missclassification error")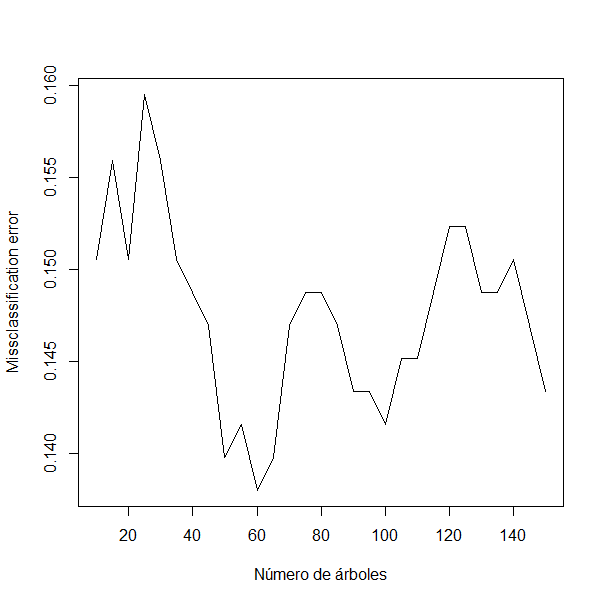
Porcentaje de clasificación errónea $vs.$ número de replicaciones.

Figura 28.2: Porcentaje de clasificación errónea \(vs.\) número de replicaciones.

La función train() del paquete caret es otra alternativa para entrenar un algoritmo de bagging en R. Para ello, el argumento method debe tomar el valor "treebag". Este algoritmo no incluye hiperparámetros a optimizar. Dado que se ha obtenido recursivamente el número óptimo de replicaciones, se puede entrenar el modelo con el valor obtenido y comprobar que el porcentaje de clasificación errónea es el mismo. Se observa que si se entrena un modelo bagging con 60 replicaciones, la accuracy del modelo (el porcentaje de observaciones clasificadas correctamente) es del 86,93%; es decir, el porcentaje de clasificación errónea es del 13,07%, similar al obtenido anteriormente con la función bagging (13,79%).199

set.seed(101)
model_bag <- train(
  CLS_PRO_pro13 ~ .,
  data = dp_entr,
  method = "treebag",
  trControl = trainControl(method = "cv", number = 10),
  nbagg = 60, 
  control = rpart.control(minsplit = 2, cp = 0)
)
# se muestra la salida del modelo
model_bag

Bagged CART 

558 samples
 17 predictor
  2 classes: 'S', 'N' 

No pre-processing
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 502, 502, 502, 503, 503, 502, ... 
Resampling results:

  Accuracy   Kappa    
  0.8692532  0.7385449

28.2.3 Interpretación de variables en el bagging

Una de las principales desventajas de los algoritmos ensamblados (incluido el bagging) es que, mientras que los modelos débiles son interpretables, el metamodelo resultante no lo es. Pese a esto, aún es posible hacer inferencias sobre la influencia (importancia) de cada una de las variables predictoras en el modelo entrenado. La manera de medir la importancia de las variables incluidas en un árbol es medir, para cada una de ellas, la reducción de la función de pérdida que se le atribuye en cada partición. Dado que una variable puede utilizarse varias veces para dividir el árbol, la importancia total de esa variable será la suma de la reducción de la función de pérdida que se le atribuya por todas las particiones en las que intervenga. En el caso particular del bagging el proceso es similar: para cada árbol, se calcula la reducción de la función de pérdida en todas las divisiones y se obtiene la reducción total sumando las reducciones calculadas en cada uno de los árboles que forman el metamodelo. El paquete ipred, en el que se encuentra la función bagging(), no captura la información requerida para calcular la importancia de las variables. Sin embargo, el paquete caret sí lo hace. La función vip() del paquete vip permite construir un gráfico de importancia (véase Fig. 28.3).

library("vip")
vip(model_bag, num_features = 15,
    aesthetics = list(color = "skyblue", fill = "skyblue"))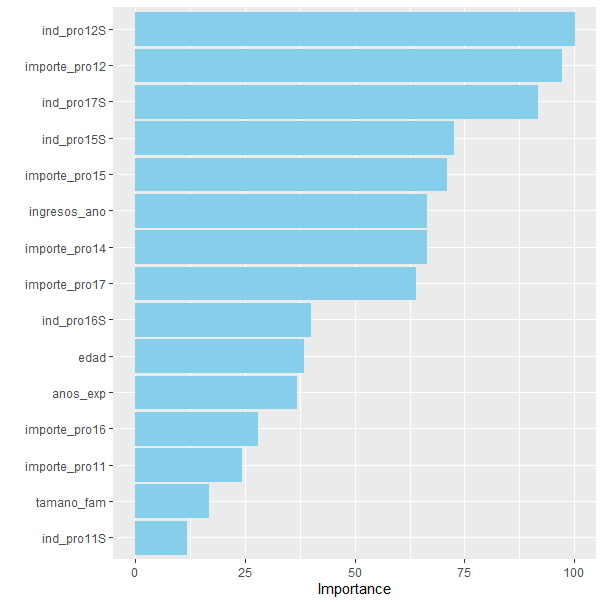
Importancia de las variables incluidas en el modelo $bagging$.

Figura 28.3: Importancia de las variables incluidas en el modelo \(bagging\).

La Fig. 28.3 muestra que las variables más importantes en el modelo bagging entrenado para predecir si un cliente comprará o no el tensiómetro digital son: si ha comprado la depiladora eléctrica, cuánto importe ha gastado en ese producto, si ha comprado el estimulador muscular y si ha comprado el smartchwatch fitness.

28.3 \(\textit{Random}\) \(\textit{forest}\)

Random forest (bosque aleatorio) es un algoritmo básico en el marco del paradigma bagging. Fue desarrollado por primera vez por T. K. Ho (1995). Sin embargo, fueron Cutler & Zhao (1999) y Breiman (2001) quienes formularon una versión extendida del modelo y registraron Random forest como marca comercial. Funciona igual que el bagging, con la salvedad de que el random forest establece una limitación artificial a la selección de variables al no considerar todas en cada árbol. El bagging considera las mismas variables para construir cada árbol con el objetivo de minimizar su entropía, y, por tanto, todos los árboles suelen tener un aspecto similar. Esto lleva a que las predicciones dadas por los árboles estén altamente correlacionadas. El modelo random forest evita este problema mediante la agregación de una fuente de variabilidad aleatoria adicional, provocando así una mayor diversidad entre los árboles del bosque. En concreto, se obliga a cada árbol a usar solo un subconjunto de los predictores a la hora de dividirse en la fase de crecimiento. Esta forma de proceder proporciona a algunas variables mayor probabilidad de ser seleccionadas y, al generar árboles únicos y no correlacionados, proporciona una estructura de decisión final más fiable. En la Fig. 28.4 puede verse un ejemplo de random forest.

Ejemplo de $random$ $forest$.

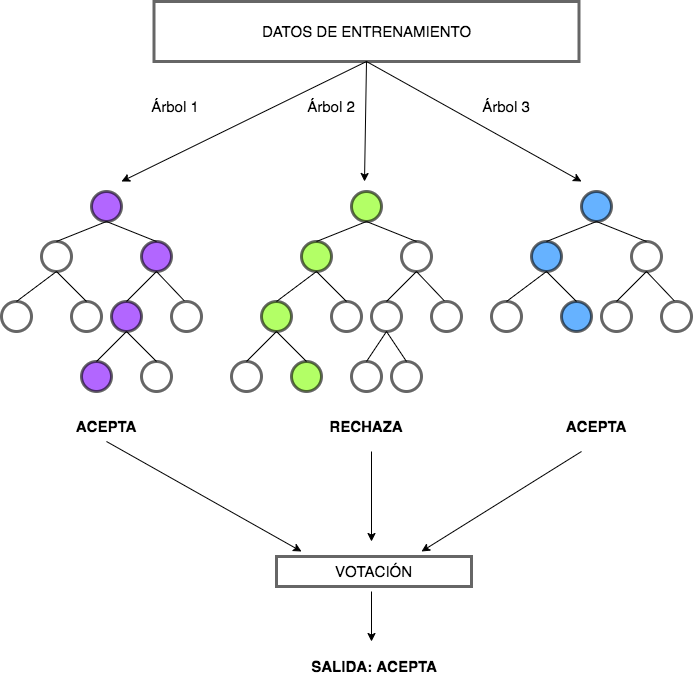
Figura 28.4: Ejemplo de \(random\) \(forest\).

En general, es mejor que el random forest esté formado por una gran cantidad de árboles (por lo menos 100) para suavizar el impacto de valores atípicos. Sin embargo, la tasa de efectividad disminuye a medida que se incorporan más árboles. Llegado a cierto punto, los nuevos árboles no aportan una mejora significativa al modelo, pero sí incrementan los tiempos de procesamiento.

El modelo random forest es rápido de entrenar y es una buena técnica para obtener un modelo de referencia. Aunque funcionan bien en la interpretación de patrones complejos y son versátiles, se ven superados, en muchas ocasiones, por otras técnicas, como por ejemplo el gradient boosting (Cap. 29).

Los random forest se han vuelto populares porque suelen proporcionar un muy buen rendimiento con los valores predeterminados de los hiperparámetros en las distintas implementaciones. En efecto, a pesar de tener muchos hiperparámetros, los valores por defecto de dichos hiperparámetros tienden a proporcionar buenos resultados en la predicción. Los hiperparámetros más importantes que hay que ajustar al entrenar un modelo random forest son: el número de árboles (\(K\)), el número de variables incluidas en el subconjunto aleatorio en cada división (mtry), la complejidad de cada árbol, el esquema de muestreo y la regla de división a utilizar durante la construcción del árbol.

28.3.1 Número de árboles (\(K\))

El primer hiperparámetro a ajustar es el número de árboles que componen el bosque aleatorio. Su valor debe ser lo suficientemente grande como para que la tasa de error se estabilice. La regla general es que el valor mínimo de árboles sea 10 veces el número de variables incluidas en el modelo. Sin embargo, cuando se tienen en cuenta otros hiperparámetros, es posible que el número de árboles se vea afectado. El tiempo de procesamiento aumenta linealmente con la cantidad de árboles incluidos, pero cuantos más se incluyan, más estables serán las estimaciones del error de clasificación o predicción.

28.3.2 Número de variables a considerar (mtry)

mtry es el hiperparámetro encargado de controlar la aleatorización de las variables utilizadas para las particiones de los árboles. Este hiperparámetro ayuda al equilibrio entre la baja correlación entre los árboles y una razonable potencia predictiva. Existe un valor predeterminado para este hiperparámetro que se puede utilizar en caso de no querer o no poder ajustarlo. En problemas de regresión, se determina que \(mtry=\frac{p}{3}\) siendo \(p\) el número de variables predictoras incluidas en el modelo. Cuando se trata de clasificar el valor predeterminado es \(mtry=\sqrt p\). Cuando hay pocas variables relevantes, es decir, los datos son “muy ruidosos”, un valor elevado de mtry tiende a proporcionar mejores resultados, pues otorga mayor probabilidad a la selección de tales variables. En cambio, cuando muchas variables son importantes, funciona mejor un valor bajo de mtry.

28.3.3 Complejidad de los árboles

A los árboles que forman parte de un bosque aleatorio se les puede controlar su profundidad y su complejidad como se vio en el Cap. 24, ajustando los hiperparámetros de profundidad máxima permitida, tamaño del nodo o cantidad máxima de nodos terminales.

El tamaño del nodo (número de observaciones en el nodo) es el hiperparámetro más común para controlar la complejidad del árbol y la mayoría de las implementaciones usan los valores predeterminados de 1 para árboles de clasificación y 5 para los árboles de regresión, dado que estos valores tienden a producir buenos resultados. Si se quiere controlar el tiempo de procesamiento, se pueden conseguir reducciones significativas del tiempo aumentando el tamaño del nodo, si bien impactando de manera marginal en el error estimado.

28.3.4 Esquema de muestreo

Por defecto, el random forest tiene como esquema de muestreo el bootstrapping. Sin embargo, el esquema de muestreo se puede ajustar tanto en el tamaño de la muestra como en el diseño muestral (con o sin reposición). El hiperparámetro de tamaño de muestra determina cuántas observaciones se extraen para el entrenamiento de cada árbol. Cuanto menor sea el tamaño muestral, menor será la correlación entre los árboles, lo cual puede llevar a mejores resultados de precisión en la predicción. La forma de determinar el tamaño muestral óptimo puede hallarse evaluando algunos valores que oscilen entre el 25% y el 100%, y en el caso de que haya variables categóricas con un número de observaciones muy distinto en sus categorías (lo cual implica un número pequeño en alguna de ellas), se puede proceder mediante muestreo con reposición.

28.3.5 Regla de división

Por defecto, la regla de división que utilizan los árboles de decisión que conforman un random forest es la que se presentó en el Cap. 24. Esto es, en el caso de regresión se selecciona la división que minimiza la desviación típica \((\sigma)\); y en el caso de clasificación, la división que minimiza la impureza de Gini o la entropía.

28.3.6 Procedimiento con R: la función randomForest()

Para entrenar un modelo random forest se utiliza la función randomForest() del paquete randomForest de R:

randomForest(formula, data=..., ...)
randomForest(x, y, xtest, ytest, ntree=500, mtry, ...)
  • formula: indica cuál es la variable respuesta y cuáles son las variables predictoras, \(Y \sim X_1 + ... + X_p\).
  • data: conjunto de datos con el que entrenar el árbol de acuerdo a la fórmula indicada.
  • x: conjunto de datos de entrenamiento que contiene los predictores.
  • y: vector respuesta con las clases o valores de la variable respuesta.
  • xtest: conjunto de datos que contiene los predictores del conjunto de datos de validación.
  • ytest: variable respuesta del conjunto de datos de validación.
  • ntree: número de árboles a construir en el modelo.
  • mtry: número de variables seleccionadas aleatoriamente como candidatas en cada partición.

28.3.7 Aplicación del modelo random forest en R

En esta sección se aplica el modelo random forest al mismo ejemplo que en el caso del bagging. El conjunto de datos es dp_entry se encuentra en el paquete CDR. Se quiere predecir si un cliente va a comprar o no el nuevo producto (un tensiómetro digital) en función de los productos que ha comprado previamente, el importe que gasta en ellos y otras características como, por ejemplo, su nivel educativo.

Este algoritmo, al estar basado en árboles de clasificación, tiene los mismos requisitos para el entrenamiento que tenían dichos árboles. En el resultado obtenido, se puede ver que el hiperparámetro mtry se ha fijado en 10 variables, pues proporciona el mejor porcentaje de clasificaciopnes correctas (accuracy).

# se fija la semilla aleatoria
set.seed(101)

# se entrena el modelo
model <- train(CLS_PRO_pro13~., data=dp_entr_NUM, 
             method="rf", metric="Accuracy", ntree=500,
             trControl=trainControl(method="cv", 
                                    number=10, 
                                    classProbs = TRUE))
# se muestra la salida del modelo
model

Random Forest 

558 samples
 19 predictor
  2 classes: 'S', 'N' 

No pre-processing
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 502, 502, 502, 503, 503, 502, ... 
Resampling results across tuning parameters:

  mtry  Accuracy   Kappa    
   2    0.8602922  0.7206238
  10    0.8620455  0.7241029
  19    0.8620130  0.7240248

Accuracy was used to select the optimal model using the largest value.
The final value used for the model was mtry = 10.

Los resultados de la validación cruzada se pueden ver en la Fig. 28.5. Se observa como la el porcentaje de clasificaciones correctas oscila entre el 80 % y el 95 %.

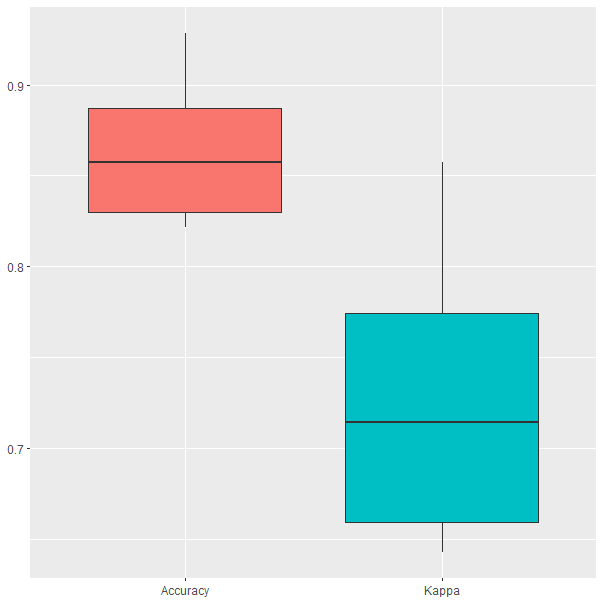
Resultados del modelo $random$ $forest$ durante el proceso de validación cruzada.

Figura 28.5: Resultados del modelo \(random\) \(forest\) durante el proceso de validación cruzada.

Finalmente, aunque el random forest generado está compuesto por 500 árboles, se puede acceder a cualquiera de ellos para estudiarlo en profundidad. Para ello, es necesario instalar el paquete reprtree desde el repositorio https://github.com/araastat/reprtree.

devtools::install_github('araastat/reprtree')

En el siguiente resultado se pueden observar las decisiones que se toman en el árbol de forma tabulada: qué variable se utiliza para la partición, cuál es el valor que decide la división, si se trata de un nodo terminal (-1) o no (1) y la predicción del nodo, que es NA si no es un nodo terminal.

set.seed(101)
rf <- randomForest(CLS_PRO_pro13~., data = dp_entr_NUM, ntree=500,
                   mtry=unlist(model$bestTune))

# se observa el árbol número 205
tree205 <- getTree(rf, 205, labelVar=TRUE)

head(tree205[,-c(1,2)])
      split var split point status prediction
1 importe_pro15         100      1       <NA>
2 importe_pro12          60      1       <NA>
3 importe_pro16          90      1       <NA>
4  ingresos_ano      156500      1       <NA>
5 importe_pro17         150      1       <NA>
6      anos_exp          33      1       <NA>
  
tail(tree205[,-c(1,2)])
               split var split point status prediction
120                 <NA>         0.0     -1          N
121                 <NA>         0.0     -1          S
122 des_nivel_edu.BASICO         0.5      1       <NA>
123                 <NA>         0.0     -1          S
124                 <NA>         0.0     -1          S
125                 <NA>         0.0     -1          N

Este árbol se muestra en la Fig. 28.6.

library("reprtree")
plot.getTree(rf, k=205)
Árbol número 205 del $random$ $forest$ entrenado.

Figura 28.6: Árbol número 205 del \(random\) \(forest\) entrenado.

Sin embargo, el método por el que se representa gráficamente no es muy claro y puede llevar a confusión o dificultar la interpretación del árbol. Si se desea estudiar el árbol, hasta un cierto nivel, se puede incluir el argumento depth. El árbol, ahora con una profundidad de 5 ramas, puede verse en la Fig. 28.7.

plot.getTree(rf, k=205, depth = 5)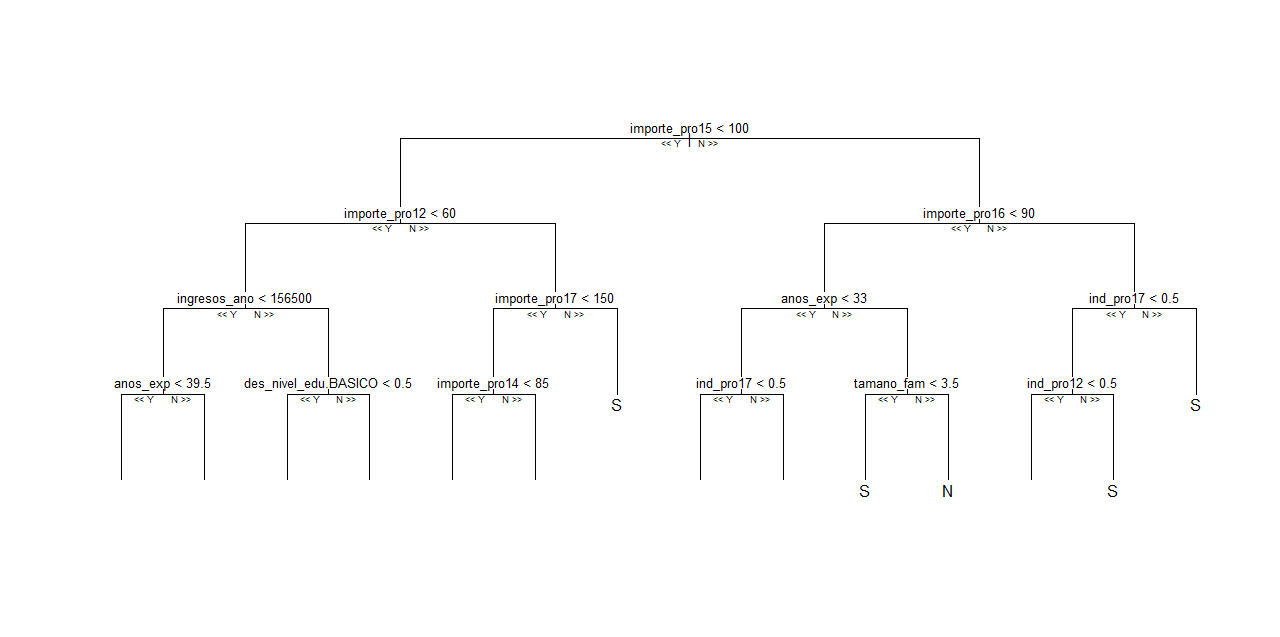
Árbol número 205 del $random$ $forest$ entrenado hasta la capa 5.

Figura 28.7: Árbol número 205 del \(random\) \(forest\) entrenado hasta la capa 5.

28.3.7.1 Aplicación del modelo random forest con ajuste automático

En este segundo ejemplo se pretende mejorar la precisión del modelo anterior. Para ello, se procede al ajuste automático de los hiperparámetros de dicho algoritmo. De los mencionados anteriormente, solo se va a ajustar automáticamente mtry, que es el único incluido el método rf.

modelLookup("rf")
  model parameter                         label forReg forClass probModel
1    rf      mtry #Randomly Selected Predictors   TRUE     TRUE      TRUE

Para ajustar el número de árboles y el resto de hiperparámetros, se puede iterar el modelo y probar distintos valores. En una red de opciones se incluyen los valores a probar para el hiperparámetro mtry.

# Se especifica un rango de valores posibles de mtry
tuneGrid <- expand.grid(mtry = 1:18)

A continuación, se entrena el modelo para que se ajuste al valor de mtry que maximice el rendimiento predictivo del modelo.

# se fija la semilla aleatoria
set.seed(101)
# se entrena el modelo
model <- train(CLS_PRO_pro13 ~ ., data=dp_entr_NUM, 
               method = "rf", metric = "Accuracy",
               tuneGrid = tuneGrid,
               trControl = trainControl(classProbs = TRUE))
# se muestra la salida del modelo
model

Random Forest 
558 samples
 19 predictor
  2 classes: 'S', 'N' 

No pre-processing
Resampling: Bootstrapped (25 reps) 
Summary of sample sizes: 558, 558, 558, 558, 558, 558, ... 
Resampling results across tuning parameters:

  mtry  Accuracy   Kappa    
   1    0.8641354  0.7283098
   2    0.8650087  0.7298376
   3    0.8629614  0.7256812
   4    0.8635609  0.7268514
   5    0.8639559  0.7276250
   6    0.8612659  0.7222420
   7    0.8604934  0.7206476
   8    0.8610116  0.7216937
   9    0.8590645  0.7177882
  10    0.8589073  0.7174718
  11    0.8607248  0.7211179
  12    0.8583609  0.7163903
  13    0.8587296  0.7170933
  14    0.8587384  0.7171642
  15    0.8583195  0.7163106
  16    0.8585407  0.7167355
  17    0.8573597  0.7144030
  18    0.8581404  0.7159558

Accuracy was used to select the optimal model using the largest value.
The final value used for the model was mtry = 2.

Mientras que en el ejemplo anterior el algoritmo solo probó tres valores de mtry, esta vez se realiza una prueba exhaustiva de valores. En el primer ejemplo, el valor del hiperparámetro era mtry=10, pero ahora se ha reajustado a mtry=2. Esto es equivalente a decir que seleccionar tan solo 2 variables en cada partición proporciona mejores resultados que seleccionar 10, como en el ejemplo anterior. Finalmente, en la Fig. 28.8 se pueden observar los resultados obtenidos durante el proceso de validación cruzada. Se observa cómo no solo el porcentaje de clasificaciones correctas es mayor que en el ejemplo anterior, sino que además los resultados tienen menos dispersión.

ggplot(melt(model$resample[,-4]), aes(x = variable, y = value, fill=variable)) + 
  geom_boxplot(show.legend=FALSE) + 
  xlab(NULL) + ylab(NULL)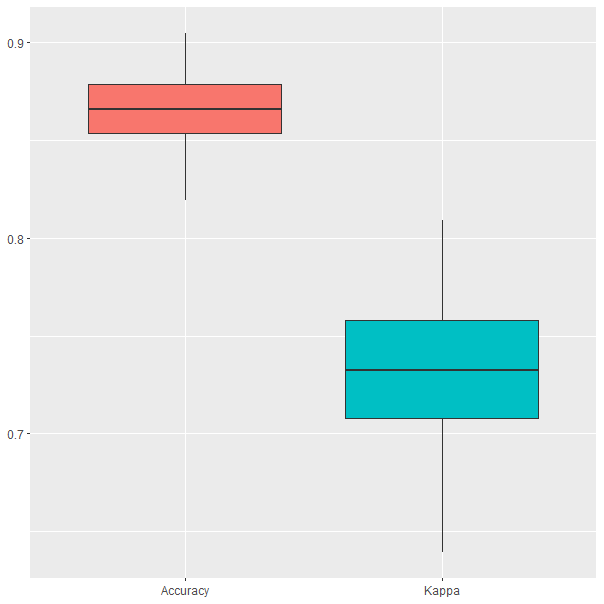
Resultados obtenidos por el random forest con ajuste automático durante el proceso de validación cruzada.

Figura 28.8: Resultados obtenidos por el random forest con ajuste automático durante el proceso de validación cruzada.

Resumen

En este capítulo se introduce al lector en el bagging y el algoritmo de aprendizaje supervisado conocido como random forest. En concreto:

  • Se presenta el concepto de aprendizaje ensamblado y se profundiza en uno de sus paradigmas: el bagging.

  • Se implementa el bagging en R a través de un caso de clasificación binaria.

  • Se expone cómo medir la importancia de las variables incluidas en un modelo bagging para facilitar su interpretación.

  • Se explica el modelo random forest, fundamentado en los árboles decisión y en el bagging. También se exponen los hiperparámetros más importantes para ajustar el modelo con mayor porcentaje de clasificaciones correctas.

  • Se presenta un ejemplo de clasificación binaria utilizando el modelo random forest en R.