Skip to main content

Fundamentos de ciencia de datos con R

Capítulo 25 Máquinas de vector soporte

Ramón A. Carrasco\(^{a}\), Itzcóatl Bueno\(^{a,\hspace{0,05cm}b}\) y José-María Montero\(^{c}\)

\(^{a}\)Universidad Complutense de Madrid
\(^{b}\)Instituto Nacional de Estadística
\(^{c}\)Universidad de Castilla-La Mancha

25.1 Introducción

Aunque las máquinas de vector soporte (SVM por sus siglas inglés: support vector machines) se desarrollaron en los años 90 dentro de la comunidad informática (Boser et al., 1992; Cortes & Vapnik, 1995) como un método de clasificación binaria, su aplicación se ha extendido a problemas de clasificación múltiple y de regresión. Como técnica de clasificación, las SVM son similares a la regresión logística (quizás la técnica más popular en este campo; véase Cap. 16), pero las SVM ponen el énfasis en el concepto de margen.191 Entrando un poco más en detalle, el margen es la distancia perpendicular desde un hiperplano separador dado hasta la observación del conjunto de entrenamiento más cercana a él. Dado un conjunto de observaciones que puede ser separado por un hiperplano, entonces puede ser separado por un número infinito de ellos (siempre se puede mover el hiperplano un poquito hacia arriba o hacia abajo, o rotarlo, sin que toque ninguna observación), se denomina hiperplano de máximo margen a aquel para el cual el margen es mayor. La utilización de un hiperplano separador es una característica propia de las SVM respecto del análisis discriminante lineal, la regresión logística, los árboles de decisión, el bagging y el boosting.

La observación del conjunto de entrenamiento más cercana al hiperplano separador con el máximo margen (criterio natural para elegir el hiperplano separador) se denomina vector soporte y puede haber varias que estén a la misma distancia; en este caso hay varios vectores soporte. Nótese que si estas observaciones cambian, aunque sea mínimamente, también cambiará el hiperplano de máximo margen. Por el contrario, las demás observaciones no tienen influencia alguna en dicho hiperplano.

Aunque los clasificadores de máximo margen pudiesen parecer la forma natural de llevar a cabo una clasificación en el caso de que exista un hiperplano separador, en muchas ocasiones tal hiperplano no existe. En tales casos, la solución pasa por suavizar el concepto de “hiperplano separador” hasta el de “hiperplano que casi separa las dos clases”, así como por relajar el concepto de “margen” y pasar a utilizar el de “margen suave”. Pues bien, esta generalización del clasificador de máximo margen al caso no separable es lo que se conoce como clasificador basado en vectores soportes.

En otros términos, las SVM toleran la clasificación errónea de unas pocas observaciones del conjunto de entrenamiento (permitiendo que esté en el lado equivocado del margen, o incluso en el lado equivocado del hiperplano) si ello favorece el porcentaje de clasificaciones correctas en el conjunto de validación. Para gobernar el nivel de tolerancia, utilizan un hiperparámetro, \(C\), que toma el valor \(0\) cuando la tolerancia es nula (se estaría en el caso del clasificador de máximo margen); a medida que incrementa su valor, el margen aumenta, aumentando también el grado de tolerancia. En definitiva, \(C\) es un hiperparámetro que controla el trade off entre sesgo y varianza cuyo valor óptimo se obtiene por validación cruzada. Valores pequeños de \(C\) implican márgenes pequeños que raramente son violados, lo que implica poco sesgo y mucha varianza. Por el contrario, cuando el valor de \(C\) aumenta los márgenes aumentan (permitiendo algunas violaciones), lo que implica más sesgo pero menos varianza.

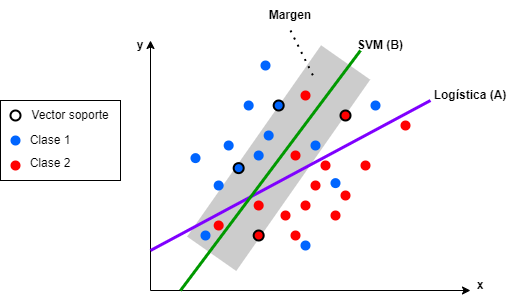
SVM $vs.$ regresión logística.

Figura 25.1: SVM \(vs.\) regresión logística.

La Fig. 25.1 muestra varias cosas:

  • Que la regresión logística divide las observaciones en dos clases, de tal forma que se minimice la distancia entre las observaciones y la frontera de decisión (A).

  • Que la frontera de decisión de la SVM (B) separa los datos en dos clases, pero maximizando la distancia entre esta y las observaciones pertenecientes a ambas clases. El margen es la distancia entre la frontera de decisión y los puntos más cercanos, si bien en el gráfico se muestra el caso de un margen suave (posteriormente se hará referencia a él) que permite que algunas observaciones queden dentro de él.

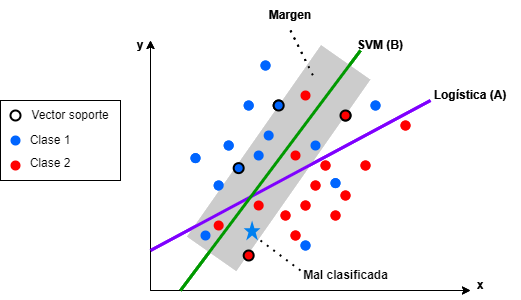
SVM $vs.$ regresión logística: observación mal clasificada con regresión logística, pero no con SVM.

Figura 25.2: SVM \(vs.\) regresión logística: observación mal clasificada con regresión logística, pero no con SVM.

El margen es una parte clave del SVM, puesto que evita clasificaciones erróneas de casos futuros como podría pasar en el caso de la regresión logística, tal y como se ilustra en la Fig. 25.2, donde la regresión logística clasifica mal la observación representada con una estrella. Cuanto mayor sea este margen, mayor será la capacidad para clasificar correctamente estos puntos.

Como se avanzó anteriormente, en problemas reales, es difícil que los discriminantes lineales vistos en el Cap. 21 logren una línea que divida perfectamente las categorías a clasificar. Sin embargo, en las SVM se incluye en la función objetivo (que mide la calidad del ajuste de los datos de entrenamiento) una penalización a los puntos que queden del lado equivocado del límite de decisión. En caso de que los datos puedan ser separados linealmente, la penalización será nula y se maximizará el margen. Si los datos no son linealmente separables, el mejor ajuste vendrá dado por el equilibrio entre una pequeña penalización del error total y un margen de decisión grande. La penalización a una observación mal clasificada es proporcional a su distancia a la frontera de decisión.

Dicho lo anterior, las SVM también tienen desventajas reseñables. En primer lugar, no son recomendables con conjuntos de datos grandes porque la complejidad de entrenamiento es elevada. Además, no funcionan bien cuando los datos tienen mucho ruido, es decir, cuando las clases se superponen. Finalmente, si el conjunto de datos de entrenamiento tiene más variables que observaciones, su rendimiento disminuye significativamente.

25.2 Algoritmo SVM para clasificación binaria

El algoritmo por el que se obtiene un modelo SVM (Vapnik, 1997) se basa en la ecuación del hiperplano compuesta por dos hiperparámetros: un vector de números reales \(\bf{w}\) de la misma dimensión que el vector de variables de entrada \(\bf x\), y un número real \(b\) tal que:

\[\begin{equation} {\bf{w}}^{\prime} {\bf{x}} - b= 0, \end{equation}\]

donde \({\bf{w}}^{\prime} {\bf{x}}=w_{1}x_1 + w_{2}x_{2} + \dots + w_{p}x_{p}\), siendo \(p\) el número de variables incluidas en \(x\). De este modo, la predicción para una instancia (observación) de \(x_j, \hspace{0,1cm} j=1,2,...,N\) viene dada por:

\[\begin{equation} y_j=sign( {\bf{w}}^{\prime} {\bf{x}_j} - b), \end{equation}\]

siendo \(sign\) el operador signo, que devuelve +1 para cualquier valor positivo de la variable respuesta y -1 para los valores negativos de la misma. En otros términos, las observaciones con valor de la variable respuesta +1 corresponden a una de sus dos clases y aquellos que producen un valor de la variable respuesta -1 pertenecen a la otra. Por tanto, en principio, el problema que hay que resolver es obtener los valores de los parámetros \(w\) y \(b\) que optimicen el resultado de la clasificación. Dichos valores se obtienen resolviendo el siguiente problema de optimización con restricciones:

\[\begin{eqnarray} {\bf{w}}^{\prime} {\bf{x}}_j - b \geq 1 \textrm{ si } y_j = +1 & \textrm{ y } \\ {\bf{w}}^{\prime} {\bf{x}}_j - b \leq 1 \textrm{ si } y_j = -1 & \end{eqnarray}\]

Pero, como el objetivo del problema de optimización es maximizar el margen en torno a la frontera de decisión, es necesario minimizar la norma euclídea de \(\bf{w}\) y, por tanto, el problema a resolver es:

25.3 ¿Y si tengo más de dos clases?

Hasta ahora se ha presentado la SVM como un algoritmo aplicable solo a la clasificación en dos clases pero ¿y si se tienen más de dos clases? En general, hay dos enfoques para resolver esta cuestión: \((i)\) uno contra todos (OVA, por one vs. all) y \((ii)\) uno contra uno (OVO, por one vs. one). En el enfoque OVA, se ajusta una SVM para cada clase, es decir, una clase contra las demás, y la observación se clasifica en la clase para la cual el margen es mayor. En cambio, en el enfoque OVO se ajustan todas las SVM por pares y se clasifica a la clase que gane las competiciones por pares.

25.4 Truco del kernel: tratando con la no linealidad

Las SVM funcionan muy bien si la separación entre clases es lineal. Sin embargo, si la separación es más compleja se intenta transformar el espacio en otro de mayor dimensionalidad donde las clases sí sean separables linealmente. Y ello porque en un espacio de alta dimensión existe una mayor probabilidad de que los datos se vuelvan separables linealmente. Para que las clases sean linealmente separables, el modelo SVM se extiende incluyendo la función de pérdida (\(\ell\)) hinge loss (Gentile & Warmuth, 1998; Lee & Lin, 2013) definida como:

\[\begin{equation} \ell(y_i) = \max(0,1-y_i({\bf{w}} {\bf{x}}_j-b)), \end{equation}\]

tal que los puntos que están lejos de los márgenes de decisión tienen un valor de pérdida mayor, siendo penalizados. En machine learning, esta función de pérdida, también llamada hinge, bisagra en ingles, se utiliza para entrenar clasificadores, y más concretamente para la clasificación por el margen máximo (métodos de clasificación binaria que se utilizan cuando hay una frontera lineal que separa perfectamente los datos de entrenamiento de una categoría de los de la otra), sobre todo para las SVM. La función de pérdida es cero cuando se cumplen las restricciones, es decir, si la observación se clasifica en el lado correcto de la frontera de decisión. Por otro lado, si un dato está mal clasificado, el valor obtenido con la función de pérdida es proporcional a la distancia hasta la frontera de decisión. Por tanto, el objetivo es minimizar la función de coste:

\[\begin{equation} C||{\bf{w}}||^{2}+\frac{1}{N}\sum_{j=1}^{N}{\max(0,1-y_j({\bf{w}} {\bf{x}}_i-b))}, \tag{25.1} \end{equation}\]

donde \(C\) es un hiperparámetro que controla la compensación entre incrementar el tamaño del margen y asegurar que cada \({\bf{x}}_j\) sea clasificado en el lado correcto de la frontera de decisión.

Un modelo SVM que optimiza la función de pérdida se denomina SVM de margen suave (soft-margin), mientras que el modelo original es conocido como SVM de margen estricto (hard-margin). Con hard-margin no se permiten observaciones en el margen. Con soft-margin se permiten algunas observaciones, pero no demasiadas, y el margen se amplía. La dureza o suavización del margen se controla con el hiperparámetro \(C\). La ecuación (25.1) muestra que para valores grandes de \(C\) el segundo término es despreciable, por lo que el algoritmo ignorará por completo la clasificación errónea y tratará de obtener el mayor margen posible. A medida que se reduce el valor de \(C\), se penalizan cada vez más los errores de clasificación, por lo que para cometer menos errores se sacrifica la amplitud del margen.

Como se avanzó en la sección introductoria, a veces no es posible separar los datos por un hiperplano en su espacio original. Sin embargo, el truco del kernel utiliza una función que implícitamente transforma el espacio original en un espacio de mayor dimensión, como se muestra en la Fig. 25.3. Así, es posible transformar un espacio de datos bidimensional no separable linealmente en un espacio de datos tridimensional linealmente separable usando un mapeo específico definido por \(\phi:{\bf{x}}\rightarrow\phi ({\bf x})\), donde \(\phi ({\bf x})\) es un vector de mayor dimensión que \({\bf{x}}\). Sin embargo, no se conoce la función de mapeo que funcionará en los datos. Probar con todas las transformaciones posibles podría resultar ineficiente, no llegándose a la resolución del problema de clasificación planteado.

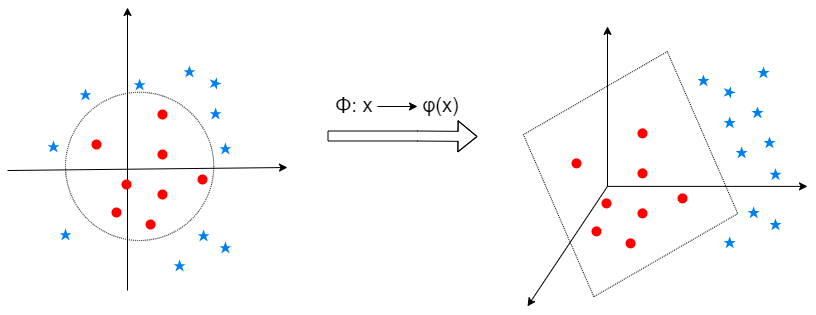
Izquierda: las dos clases en el espacio original (2-D). Derecha: las dos clases en el espacio de sobredimensionado (3-D).

Figura 25.3: Izquierda: las dos clases en el espacio original (2-D). Derecha: las dos clases en el espacio de sobredimensionado (3-D).

Se puede trabajar eficientemente en espacios de mayor dimensión sin necesidad de hacer las transformaciones explícitamente. Utilizando el truco del kernel se puede evitar este proceso costoso de transformación, no teniendo que calcular productos escalares y remplazando esta operación por otra más simple con las variables originales que proporciona el mismo resultado. A continuación se exponen algunos de estos operadores especiales, llamados kernels, que permiten llevar a cabo dicha transformación.

25.4.1 Algunos kernels populares

Los kernels (Schölkopf, Simard, et al., 1997; Schölkopf, Sung, et al., 1997) más populares en el entrenamiento de SVM están incluidos en la función svm() del paquete e1071 y se especifican en el hiperparámetro kernel. Estos kernels son:

  • Lineal: \(K({\bf{u}},{\bf{v}}) = \langle {\bf{u}},{\bf{v}}\rangle\), donde \(\langle {\bf{u}},{\bf{v}}\rangle = \sum_{i=1}^{n}{u_iv_i}\) es el producto escalar de \(\bf u\) y \(\bf v\),
  • Polinomial de grado \(\delta\): \(K({\bf{u}},{\bf{v}}) = \gamma \left(k_1+\langle {\bf{u}},{\bf{v}}\rangle\right )^\delta\),
  • Base radial: \(K({\bf{u}},{\bf{v}}) = e^{\gamma||{\bf{u}},{\bf{v}}||^2}\),
  • Sigmoidal: \(K({\bf{u}},{\bf{v}}) = \tanh\left(\gamma\langle{\bf{u}},{\bf{v}}\rangle+k_1\right)\),

donde \(\bf u\) y \(\bf u\) son vectores (en este caso de observaciones) y \(\delta\), \(\gamma\) y \(k_1\) son hiperparámetros de kernel que hay que tunear, es decir, ajustar (el ajuste se lleva a cabo de manera automática) para optimizar el rendimiento de la SVM. Los hiperparámetros a ajustar se pueden conocer utilizando la función modelLookup de caret. Por ejemplo, para una SVM con kernel de base radial son el coste, \(C\), que aparece en la ecuación (25.1) y \(\sigma\), que equivale a \(\gamma\) en la ecuación (25.1) (este hiperparámetro suele llamarse \(\gamma\) en la literatura, pero la función svm lo llama \(\sigma\)).

modelLookup("svmRadial")
      model parameter label forReg forClass probModel
1 svmRadial     sigma Sigma   TRUE     TRUE      TRUE
2 svmRadial         C  Cost   TRUE     TRUE      TRUE

25.5 Procedimiento con R: la función svm()

En el paquete e1071 de R se encuentra la función svm() que se utiliza para entrenar un modelo SVM:

svm(x, y, scale = TRUE, type = NULL, kernel = ..., ...)

donde:

  • x: conjunto de datos de entrenamiento que contiene los valores de los predictores.
  • y: vector respuesta con las clases o valores de la variable respuesta.
  • scale: booleano que indica si es necesario escalar las variables.
  • type: indica si se pretende resolver un problema de clasificación o de regresión.
  • kernel: kernel utilizado durante el entrenamiento y la predicción.

25.6 Aplicación de un modelo SVM radial con ajuste automático en R

Para llevar a cabo la aplicación en la que se centra esta sección se retoma el ejemplo expuesto en el Cap. 24, relativo a la empresa Beauty eSheep, que pretende vender tensiómetros digitales, obteniéndose las predicciones sobre si el cliente comprará o no un tensiómetro en función de una serie de variables incluidas en el conjunto de datos dp_ENTRdel paquete CDR, y que se resume en la Tabla 24.8.

Los datos utilizados para entrenar el modelo SVM se cargan desde la librería CDR. Además, para su entrenamiento se requieren las librerías caret y e1071.

Se entrena un modelo SVM con kernel radial utilizando el conjunto de entrenamiento con todas las variables numéricas. Previamente se aplica una normalización z-score (véase Cap. 9) para que todas las variables utilizadas estén la misma escala. Además, se ajustan automáticamente los hiperparámetros de dicho algoritmo (\(C\) y \(\sigma\)) durante el proceso de entrenamiento.

trControl <- trainControl(
  method = "cv",
  number = 10,
  classProbs = TRUE,
  preProcOptions = list("center"),
  summaryFunction = twoClassSummary
)

# Se especifica un rango de valores para los hiperparámetros
tuneGrid <- expand.grid(sigma = seq(from=0.1, to=0.2, by=0.05),
                        C = 10**(-2:4))

Para el entrenamiento y validación se define un remuestreo por validación cruzada con 10 grupos (véase Cap. 10). Además, se le indica al algoritmo que debe calcular las probabilidades de clase en cada remuestreo en caso de estar entrenando un modelo de clasificación. Con el argumento summaryFunction = twoClassSummary se le indica al modelo que, para evaluar la clasificación realizada, se calculen la sensibilidad, especificidad y el área bajo la curva ROC. Como se ha comentado anteriormente, conviene estandarizar los datos; esto se le indica a la función a través del argumento preProcOptions, con la opción center (téngase en cuenta que, previamente, ya se había aplicado una normalización \(z-score\) para que todas las variables estuviesen en la misma escala. A su vez, se define una red de hiperparámetros a optimizar. A través de la función train() se ajusta automáticamente el modelo con los hiperparámetros óptimos.

# Se fija la semilla aleatoria
set.seed(101)

# Se entrena el modelo
model <- train(CLS_PRO_pro13 ~ .,
             data=dp_entr_NUM,
             method="svmRadial",
             metric="ROC",
             trControl=trControl,
             tuneGrid=tuneGrid)
# se muestra la salida del modelo
model

Support Vector Machines with Radial Basis Function Kernel

558 samples
 19 predictor
  2 classes: 'S', 'N'

No pre-processing
Resampling: Cross-Validated (10 fold)
Summary of sample sizes: 502, 502, 502, 503, 503, 502, ...
Resampling results across tuning parameters:

  sigma  C      ROC        Sens       Spec
  0.10   1e-02  0.9553241  0.8785714  0.7071429
  0.10   1e-01  0.9566327  0.8924603  0.8247354
  0.10   1e+00  0.9434902  0.8604497  0.8496032
  0.10   1e+01  0.9227230  0.8460317  0.8423280
  0.10   1e+02  0.8804894  0.8567460  0.8279101
  0.10   1e+03  0.8645692  0.8674603  0.8206349
  0.10   1e+04  0.8548469  0.8423280  0.8242063
  0.15   1e-02  0.9527636  0.8535714  0.6642857
  0.15   1e-01  0.9513653  0.9105820  0.8105820
  0.15   1e+00  0.9310091  0.8783069  0.8494709
  0.15   1e+01  0.8941421  0.8531746  0.8387566
  0.15   1e+02  0.8602088  0.8781746  0.8242063
  0.15   1e+03  0.8369331  0.8458995  0.8134921
  0.15   1e+04  0.8369284  0.8637566  0.8064815
  0.20   1e-02  0.9443925  0.8535714  0.6321429
  0.20   1e-01  0.9440098  0.9250000  0.7384921
  0.20   1e+00  0.9199310  0.8818783  0.8387566
  0.20   1e+01  0.8752031  0.8674603  0.8207672
  0.20   1e+02  0.8477324  0.8674603  0.8063492
  0.20   1e+03  0.8308296  0.8638889  0.8134921
  0.20   1e+04  0.8308296  0.8638889  0.8099206

ROC was used to select the optimal model using the largest value.
The final values used for the model were sigma = 0.1 and C = 0.1.

Los argumentos que requiere la función son:

  • La formula, donde se indica la variable respuesta y qué predictores intervienen en el modelo.
  • Los datos que se van a utilizar.
  • El algoritmo a entrenar, en este caso la SVM con kernel de base radial.
  • La métrica para el evaluar el rendimiento del modelo; en caso de no indicarla, R asigna la más acorde con la variable respuesta.
  • Las opciones de entrenamiento.
  • La red de hiperparámetros a probar para determinar la combinación óptima; en este caso, \(C\) (véase la ecuación (25.1)) y \(\sigma\) (en la literatura escrita se suele llamar gamma; sin embargo, la función svm lo llama sigma). Los valores de dichos hiperparámetros en el modelo entrenado son \(\sigma=0.1\) y \(C=0.1\), véase la salida del modelo y la Fig. 25.4.
ggplot(model)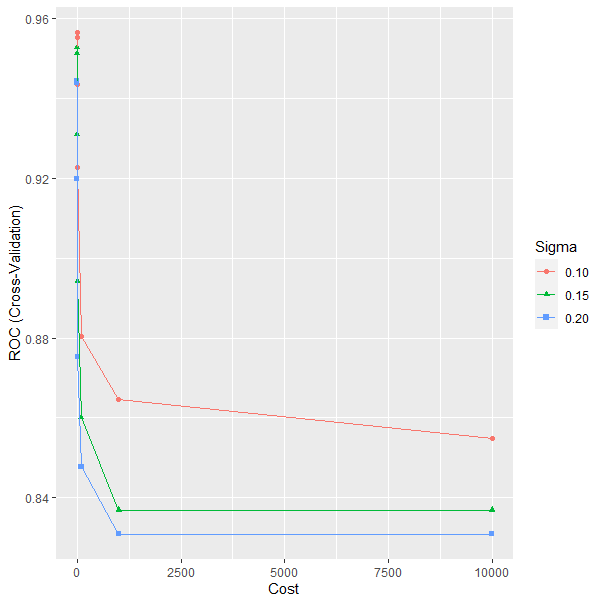
Optimización de los parámetros C y sigma de una SVM.

Figura 25.4: Optimización de los parámetros C y sigma de una SVM.

Los resultados que se derivan de la matriz de confusión correspondiente al modelo resultante son los siguientes:

set.seed(101)
confusionMatrix(predict(model), dp_entr_NUM$CLS_PRO_pro13)
Confusion Matrix and Statistics

          Reference
Prediction   S   N
         S 253  30
         N  26 249

               Accuracy : 0.8996
                 95% CI : (0.8717, 0.9233)
    No Information Rate : 0.5
    P-Value [Acc > NIR] : <2e-16

                  Kappa : 0.7993

 Mcnemar's Test P-Value : 0.6885

            Sensitivity : 0.9068
            Specificity : 0.8925
         Pos Pred Value : 0.8940
         Neg Pred Value : 0.9055
             Prevalence : 0.5000
         Detection Rate : 0.4534
   Detection Prevalence : 0.5072
      Balanced Accuracy : 0.8996

       'Positive' Class : S

Los box-plot de la Fig. 25.5 muestran un resumen del rendimiento del modelo en las diez repeticiones del proceso de validación cruzada. Se observa que la sensibilidad es superior al 85% y la especificidad supera el 75%. Estos resultados indican que el modelo entrenado es capaz de clasificar bastante bien tanto a los clientes que van a comprar el nuevo producto como a los que no lo van a hacer.

ggplot(melt(model$resample[,-4]), aes(x = variable, y = value, fill=variable)) +
  geom_boxplot(show.legend=FALSE) +
  xlab(NULL) + ylab(NULL)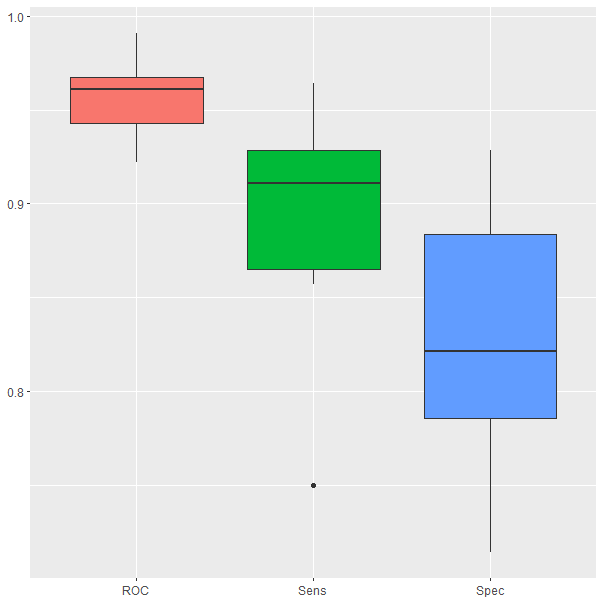
Resultados del modelo obtenidos durante la validación cruzada.

Figura 25.5: Resultados del modelo obtenidos durante la validación cruzada.

25.6.1 Importancia de las variables

En machine learning, muchos de los algoritmos de caja negra (definidos en el Cap. 4) no proporcionan información sobre la importancia que tiene cada variable en el modelo. En el caso de las SVM, como de otros algoritmos, es posible cuantificar la importancia de cada variable utilizando paquetes de R como DALEX, iml o vip.

Este último paquete incluye una función con el mismo nombre, vip(), donde para medir la importancia se indica qué métrica se utilizó en el proceso de entrenamiento del modelo. En el caso concreto de la SVM se indica que la métrica utilizada en el proceso de entrenamiento fue el área bajo la curva (metric=auc). En el argumento pred_wrapper (donde “pred” se refiere a predicción) se indica una función de medida que contenga tanto los valores observados como los valores predichos. Dado que la SVM entrenada utiliza el área bajo la curva ROC para medir el rendimiento del modelo ajustado, la función de medida indicada en pred_wrapper devolverá la probabilidad de que el modelo asigne una observación a la clase de referencia. En este ejemplo, la función de predicción se define como:

prob_si <- function(object, newdata) {
  predict(object, newdata = newdata, type = "prob")[, "S"]
}

Ejecutando la función vip() con los argumentos mencionados se genera la Fig. 25.6. Este gráfico indica, en orden descendente, la importancia de cada variable en el modelo. En este caso, la variable más importante es el importe gastado en el smartchwatch fitness, seguida muy de cerca por la variable que indica si el cliente compra o no el smartchwatch fitness. En el otro extremo, se observa que las variables que indican si el cliente tiene un nivel de educación básico o no, no son muy relevantes en la SVM entrenada.

library("vip")

set.seed(101)  
vip(model, train = dp_entr_NUM, target = "CLS_PRO_pro13", metric = "auc",
    reference_class = "S", pred_wrapper = prob_si, method="permute",
    aesthetics = list(color = "steelblue2", fill = "steelblue2"))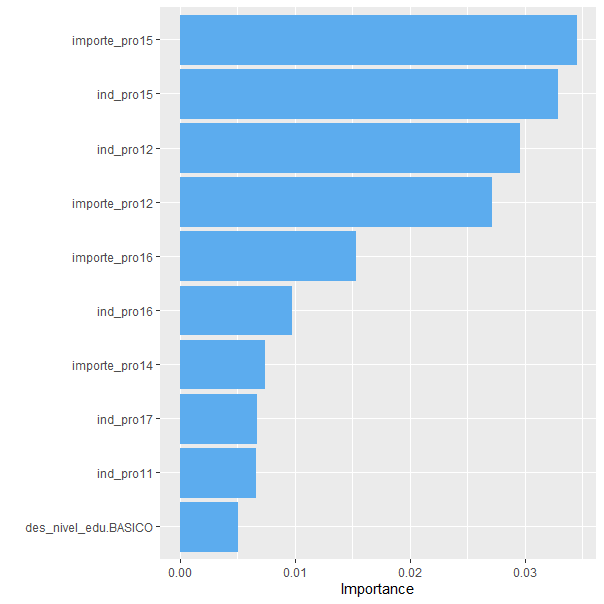
Importancia de las variables incluidas en la SVM.

Figura 25.6: Importancia de las variables incluidas en la SVM.

A partir de la Fig. 25.6 se puede concluir que, para predecir si un cliente comprará o no el tensiómetro digital, las variables que más importancia tienen son: el importe que gastó en el smartchwatch fitness, si compró o no el smartchwatch fitness, el importe que gastó en la depiladora eléctrica y si compró o no la depiladora eléctrica.

De forma similar se podrían probar el resto de kernels disponibles para el algoritmo SVM.

Resumen

En este capítulo se introduce al lector en el algoritmo de máquinas de vector soporte. En particular:

  • Se presenta el concepto de margen de decisión y se exponen las ventajas de la SVM respecto a otras técnicas de clasificación.

  • Se explica el truco del kernel cuando los datos no son separables por un hiperplano en su espacio original.

  • Se da un repaso a los kernels más utilizados.

  • Se presenta la aplicación en R de una SVM con kernel radial y ajuste automático de los hiperparámetros para la clasificación de datos con respuesta binaria.

  • Se obtiene la importancia de las variables incluidas en el modelo final.