Capítulo 9 Selección y transformación de variables

Jorge Velasco López\(^{a}\) y José-María Montero\(^{b}\)

\(^{a}\)Instituto Nacional de Estadística de España
\(^{b}\)Universidad de Castilla-La Mancha

9.1 Introducción

Como se indicó en el Cap. 8, la preparación de datos, en un contexto de ciencia de datos, consiste en transformarlos de tal forma que se puedan utilizar adecuadamente en las fases posteriores de modelado. Esta preparación o prepreprocesamiento puede ser un proceso laborioso e incluye tareas como la integración y limpieza de datos, que se detallaron en dicho capítulo.

El presente capítulo aborda las tareas relativas a la selección de variables (feature selection) y transformación de variables. La selección de variables tiene como objetivo elegir el elenco de variables más relevantes para el análisis. La transformación de variables hace referencia, básicamente, al uso de determinados procedimientos para modificar la distribución de la variable objetivo, a la ingeniería de variables (feature engineering), a la normalización y a la reducción de la dimensionalidad del problema de interés.

Se usará el conjunto de datos Madrid_Sale (disponibles en el paquete de R idealista18), con datos inmobiliarios del año 2018 para el municipio de Madrid, y los paquetes caret (Kuhn, 2008), para diversas tareas de preparación de datos y corrplot (Wei et al., 2017), para visualizar correlaciones, entre otros.

9.2 Selección de variables

Quizás, el primer gran reto al que se enfrenta el científico de datos cuando maneja grandes conjuntos de datos es la identificación de las variables que proporcionen información valiosa sobre la variable objetivo, bien se trate de un problema de regresión, bien de clasificación. En caso de que el científico de datos salga exitoso de este primer gran reto, un determinado subconjunto de variables del conjunto de datos de interés proporcionará la misma información sobre la variable objetivo que la totalidad de variables incluidas en el conjunto de datos. En consecuencia, la selección de variables involucra un conjunto de técnicas cuyo objetivo es seleccionar el subconjunto de variables predictoras más relevante para las fases de modelización. Esto es importante porque:

• Variables predictoras redundantes pueden distraer o engañar a los algoritmos de aprendizaje, lo que posiblemente se traduzca en un menor rendimiento, no solo predictivo (exactitud y precisión), sino también en términos de tiempo de computación.

• Igualmente, la inclusión de variables irrelevantes aumenta el coste computacional y dificulta la interpretabilidad.

Una adecuada selección de variables tiene ventajas importantes: \((i)\) elimina las variables con información redundante; \((ii)\) reduce el grado de complejidad de los modelos; \((iii)\) evita o reduce el sobreajuste; \((iv)\) incrementa de la precisión de las predicciones; y \((v)\) reduce la carga computacional. No obstante, es importante señalar que, antes de llevarse a cabo la selección de variables propiamente dicha, debe comprobarse la magnitud de la varianza de las variables candidatas a ser seleccionadas y de sus correlaciones dos a dos, así como si existen combinaciones lineales entre ellas (multicolinealidad). Y ello porque estas tres comprobaciones sirven para realizar una primera preselección de variables, si bien por razones técnicas y no de capacidad de explicación del comportamiento de la variable respuesta. Los métodos de selección de variables (tras la preselección anteriormente mencionada) se suelen clasificar en: \((i)\) los que utilizan la variable objetivo (supervisados); y \((ii)\) los que no (no supervisados). Debido a la complejidad de la cuestión, se pasará revista únicamente a los métodos supervisados más relevantes, que se pueden dividir en:

• Métodos tipo filtro, que puntúan de mayor a menor cada variable predictora en base a su capacidad predictiva y seleccionan un subconjunto de ellas en base a dichas puntuaciones (Brownlee, 2020).

• Métodos tipo envoltura (wrapper), que eligen el subconjunto de variables que dan como resultado el modelo con mayores prestaciones en cuanto a calidad de resultados y eficiencia: error de predicción o clasificación, precisión, tiempo de computación…

• Métodos intrínsecos (o embedded), que seleccionan las variables automáticamente como parte del ajuste del modelo durante el entrenamiento; tal es el caso de algunos modelos de regresión penalizados, como Lasso, árboles de decisión y bosques aleatorios (random forests).

9.2.1 Preselección de variables

9.2.1.1 Varianza nula

Uno de los aspectos fundamentales en la selección de variables es comprobar si su varianza es cero o cercana a cero porque, si es así, sus valores son iguales o similares, respectivamente, y, por tanto, esas variables estarán perfectamente o cuasiperfectamente correlacionadas con el término independiente del modelo, con lo cual, en el mejor de los casos, solo añadirán ruido al modelo. Además, este tipo de variables causan problemas a la hora de dividir el conjunto de datos en subconjuntos de entrenamiento, validación y test. Las causas de una nula o muy pequeña variabilidad pueden estar en haber medido la variable en una escala inapropiada para la variable o en haber expandido una variable politómica en varias dicotómicas (una por categoría), entre otras. En el primer caso, un cambio de escala puede evitar el problema de la colinealidad. Otra opción más drástica es la eliminación de la variable.

A continuación, se comprueba si las variables del conjunto de datos Madrid_Sale tienen varianza cero. Para ello se utiliza la función nearZeroVar() del paquete caret.

Se seleccionan en primer lugar las variables numéricas en el conjunto de datos Madrid_Sale_num.

library("idealista18")
library("tidyverse")
library("caret")

Madrid_Sale <- as.data.frame(Madrid_Sale)
numeric_cols <- sapply(Madrid_Sale, is.numeric)
Madrid_Sale_num <- Madrid_Sale[, numeric_cols]

Se observa que se devuelve el valor nzv=FALSE (nzv: near zero variance) para casi todas las variables, con la excepción de PARKINGSPACEPRICE, ISDUPLEX, ISSTUDIO, ISINTOPFLOOR y BUILTTYPEID_1, que podrían descartarse como variables predictoras.

varianza <- nearZeroVar(Madrid_Sale_num, saveMetrics = T)
# Con el argumento saveMetrics, se guardan los valores que se han utilizado para los cálculos.
# Se muestran los primeros resultados
head(varianza, 2)
#>       freqRatio  percentUnique   zeroVar   nzv
#> PERIOD  2.019617   0.004218742   FALSE   FALSE
#> PRICE   1.076923   2.911986500   FALSE   FALSE

Para filtrar (excluir) las variables que se descartan como predictoras, se procede como sigue:

Madrid_Sale_num <- Madrid_Sale_num|>
  select(-c(PARKINGSPACEPRICE, ISDUPLEX, ISSTUDIO, BUILTTYPEID_1))

9.2.1.2 Correlación entre variables

Como se avanzó anteriormente, otra de las cuestiones a tener en cuenta en el proceso de selección de variables es la magnitud de las correlaciones entre las variables candidatas, pues la existencia de correlaciones elevadas tiene consecuencias perversas sobre la fiabilidad de las predicciones (o de la clasificación realizada). En el caso extremo el modelo tendrá problemas de colinealidad o multicolinealidad (véase Sec. 9.2.1.3).

Para detectar las variables con muy elevada correlación entre ellas, se le pasa la función findCorrelation() de caret, con valor 0,9, a la matriz de correlaciones lineales entre las variables susceptibles de ser seleccionadas.

madrid_cor <- cor(Madrid_Sale_num[, 1:20])
alta_corr <- findCorrelation(madrid_cor, cutoff = .9)

Con ello, se comprueba que la variable HASPARKINGSPACE tiene correlaciones superiores a 0,9 con varias de las variables predictoras, procediéndose a su eliminación.

Madrid_Sale_num <- Madrid_Sale_num[, -alta_corr]

La Fig. 9.1, generada con el paquete corrplot, muestra las correlaciones existentes entre las primeras variables predictoras.

library("corrplot")

matriz_corr <- cor(Madrid_Sale_num[, 1:8])
corrplot(matriz_corr, method = "circle")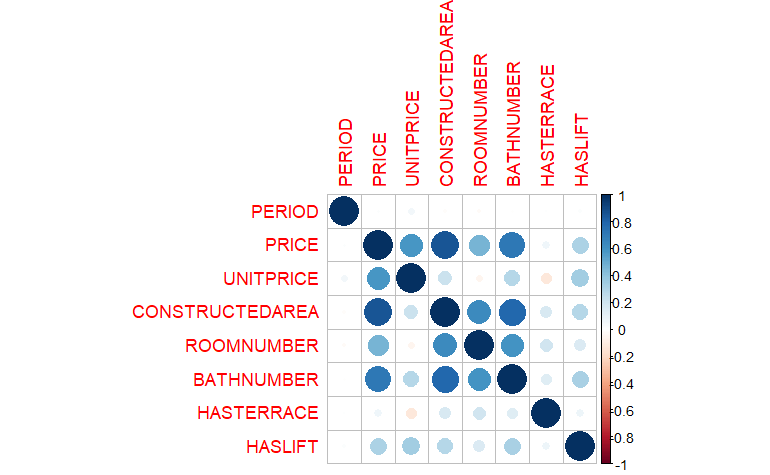

Figura 9.1: Matriz de correlaciones topada en 0,9.

Se aprecia que ya no hay variables altamente correlacionadas.

9.2.1.3 Combinaciones lineales

En la práctica, en la mayoría de los casos, por ejemplo en las regresiones lineales, las variables que se utilizan como predictoras no son ortogonales, sino que tienen cierto grado de dependencia lineal entre ellas. Si dicho grado es moderado, las consecuencias de la no ortogonalidad en la predicción no son graves, pero en los casos de dependencia lineal cuasiperfecta las inferencias resultantes del modelo estimado distan mucho de la realidad. Dichas consecuencias son aún más graves en el caso de que las combinaciones lineales sean perfectas. Por ello, la existencia de colinealidad o combinaciones lineales entre las variables seleccionables también es una circunstancia a evitar. En el caso de que los predictores (o varios de ellos) conformen una o varias combinaciones (o cuasicombinaciones) lineales, no se puede conocer el impacto específico de cada uno de ellos en la variable objetivo, pues dichos impactos se solapan unos con otros. Además, como se ha avanzado, las predicciones no son fiables, entre otras cosas (véase Peña, 2002). Y es que se le está pidiendo al conjunto de datos en estudio más información sobre la variable objetivo de la que realmente tiene. Entre otros modelos, la regresión lineal y la regresión logística parten del supuesto de no colinealidad o multicolinealidad entre las variables, por lo que no debería haber variables correlacionadas, ni dos a dos, ni en forma de combinación lineal entre varias de ellas.

Las principales fuentes de multicolinealidad son:

• El método utilizado en la recogida de datos (subespacios).
• Restricciones en el modelo o en la población (existencia de variables correlacionadas).
• Especificación del modelo (polinomios).
• Más variables que observaciones.

En cuanto al detalle de las consecuencias más importantes de la multicolinealidad, hay que señalar las siguientes:

• Los estimadores tendrán grandes varianzas y covarianzas.
• Las estimaciones de los coeficientes del modelo serán demasiado grandes.
• Los signos de los coeficientes estimados suelen ser distintos a los esperados.
• Pequeñas variaciones en los datos, o en la especificación del modelo, provocarán grandes cambios en los coeficientes.

En el ejemplo con los datos del conjunto Madrid_Sale se utiliza la función findLinearCombos() de caret para encontrar, en caso de que las haya, combinaciones lineales de las variables predictoras.

Madrid_Sale_num_na <- tidyr::drop_na(Madrid_Sale_num) # Es necesario eliminar los NA.
combos <- findLinearCombos(Madrid_Sale_num_na)
combos
#$remove
#NULL

Como puede comprobarse, no se encuentra ninguna combinación lineal en las variables numéricas de Madrid_Sale. En caso de existir, una solución al problema de la multicolinealidad pasa por:

• Eliminar variables predictoras que se encuentren altamente relacionadas con otras que permanecen en el modelo.

• Sustituir las variables predictoras por componentes principales (véase Cap. 32).

• Incluir información externa a los datos originales. Esta alternativa implica utilizar estimadores contraídos (de Stein o ridge) o bayesianos.

A continuación se muestra, en caso de existir, cómo se eliminarían las combinaciones lineales:

Madrid_Sale_num_na[, -combos$remove]

9.2.2 Métodos de selección de variables

Tras la preselección de variables llevada a cabo en el epígrafe anterior, procede la selección de variables, propiamente dicha, de entre las que han superado la fase previa, sobre la base de criterios de capacidad predictiva, principalmente. No obstante, también se utilizan para:

• Simplificar modelos para hacerlos más interpretables.
• Mejorar la precisión del modelo (si se ha escogido bien el subconjunto de variables).
• Reducir el tiempo de computación; sobre todo, entrenar algoritmos a mayor velocidad.
• Evitar la maldición de la dimensionalidad (o efecto Huges), que se refiere a las consecuencias no deseadas que tienen lugar cuando la dimensionalidad de un problema es muy elevada.
• Reducir la probabilidad de sobreajuste.

9.2.2.1 Métodos tipo filtro

Los métodos de selección de variables tipo filtro usan técnicas estadísticas para evaluar la relación entre cada variable predictora (o de entrada, o independiente) y la variable objetivo (o de salida, o dependiente). Generalmente, consideran la influencia de cada variable predictora sobre la variable objetivo por separado. Las puntuaciones obtenidas se utilizan como base para clasificar y elegir las variables predictoras que se utilizarán en el modelo.

La elección de las técnicas estadísticas depende del tipo de variables (objetivo y predictoras). Por ejemplo, si las variables de entrada (predictoras) y salida (objetivo) fueran numéricas, se utilizaría el coeficiente de correlación de Pearson o el de Spearman (dependiendo de si la relación entre la variable predictora y la variable objetivo es lineal o no) o el método de información mutua (véase Vergara & Estévez, 2014). Si ambas fuesen categóricas, podrían usarse medidas de asociación para tablas de contingencia \(2\times 2\) o \(R\times C\) (véanse Sec. 23.4 y 23.5). Si la de entrada fuese categórica y la de salida, numérica, la técnica adecuada sería el Análisis de la Varianza (ANOVA, véase Sec. 15.4.6.1). Si la categórica fuese la de salida y la numérica la de entrada, entonces habría que acudir a la regresión logística (véase Sec. 16.4), por ejemplo. Sin embargo, el conjunto de datos no tiene por qué tener solo un tipo de variable de entrada. Para manejar diferentes tipos de variables de entrada, se pueden seleccionar, por separado, variables de entrada numéricas y variables de entrada categóricas, usando en cada caso las técnicas apropiadas.

Estos métodos suelen eliminar solo las variables de menor interés a la hora de predecir/clasificar. Permiten ahorrar tiempo y son especialmente robustos para el sobreaprendizaje. Sin embargo, no tienen en cuenta las relaciones entre las variables, lo que puede dar lugar a seleccionar variables redundantes si es que no se ha llevado a cabo una fase de preselección.

Nota

Existen diversos paquetes, como FSelector (Romanski et al., 2013) y el mismo caret, para implementar técnicas de selección de variables. Aquí se utiliza FSinR, que contiene una serie de métodos de filtro y envoltura, que se combinan con algoritmos de búsqueda para obtener el subconjunto óptimo de variables, usando funciones para entrenar modelos de clasificación y regresión disponibles en el paquete caret. La selección de variables o características se lleva a cabo con la función FeatureSelection(), y la del algoritmo de búsqueda que se utilizará en el proceso de selección de funciones se realiza con la función searchAlgorithm(). Por su parte, los métodos de filtrado se implementan a través de la función filterEvaluator(). No debe olvidarse que, antes de realizar el proceso de selección de variables, el usuario tiene que dividir el conjunto de datos convenientemente para llevar a cabo cada operación sobre el subconjunto correcto (véase Cap. 10). Igualmente, también de manera previa, se tiene que resolver el problema de los datos faltantes.

A continuación se muestra un ejemplo para variables predictoras numéricas. Para ello, se toma una muestra del conjunto de datos Madrid_Sale_num, obtenido en la Sec. 9.2.1.1. Una vez en disposición de la muestra, primeramente se transforma la variable objetivo en categórica, siendo las categorías (intervalos) cuatro cortes de la distribución de sus valores; dicha categorización se lleva a cabo mediante binning.⁷¹ También se eliminan los registros con datos faltantes.

library("rsample")

# Se toma una muestra con el paquete rsample
set.seed(7)
Madrid_Sale_num_sample <- sample(1:nrow(Madrid_Sale_num), size = 5000, replace = FALSE)
Madrid_Sale_num_sample <- Madrid_Sale_num[Madrid_Sale_num_sample, ]
# Se realiza binning con cuatro bins
Madrid_Sale_num_sample_bin <- Madrid_Sale_num_sample |>
  mutate(price_bin = cut(PRICE, breaks = c(0, 250000, 500000, 750000, 10000000), labels = c("primerQ", "segundoQ", "tercerQ", "c"), include.lowest = TRUE)) |>
  select(price_bin, CONSTRUCTEDAREA, ROOMNUMBER, BATHNUMBER, HASTERRACE, HASLIFT)
# Se eliminan los registros con valores missing
Madrid_Sale_sample_na <- drop_na(Madrid_Sale_num_sample_bin)

Una vez discretizada la variable objetivo, se selecciona el conjunto de variables predictoras de la variable objetivo price_bin, que es la variable PRICE transformada mediante binning. Como método tipo filtro se utiliza minimum description length (MDLM), que es un método de selección de variables que se basa en una medida de la complejidad del modelo denominada “longitud mínima de la descripción” (de ahí el nombre del modelo), por lo que su objetivo es encontrar el modelo más sencillo que proporcione una explicación aceptable de los datos. Como algoritmo de búsqueda se utiliza sequential forward selection.⁷²

library("FSinR")

# Método tipo filtro MDLC (Minimum-Description_Length-Criterion)
evaluador <- filterEvaluator("MDLC")
# Se genera el algoritmo de búsqueda
buscador <- searchAlgorithm("sequentialForwardSelection")
# Se implementa el proceso, pasando a la función los dos parámetros anteriores
resultados <- featureSelection(Madrid_Sale_sample_na, "price_bin", buscador, evaluador)
# Se muestran los resultados
resultados$bestFeatures
#>      CONSTRUCTEDAREA ROOMNUMBER BATHNUMBER HASTERRACE HASLIFT
#> [1,]               0          0          0          1       0
resultados$bestValue
#> [1] 355.3439

En este caso, con los argumentos propuestos, el modelo seleccionado para explicar el comportamiento de la variable objetivo price_bin contiene únicamente el término independiente y una variable predictora: HASTERRACE.

9.2.2.2 Métodos de selección de variables tipo envoltura (wrapper)

Este enfoque realiza una búsqueda a través de diferentes combinaciones o subconjuntos de variables predictoras/clasificadoras para comprobar el efecto que tienen en la precisión del modelo (Saeys et al., 2007).

Hay varias alternativas:

• Evaluar las variables individualmente y seleccionar las \(n\) variables principales que obtienen unas buenas prestaciones, aunque se pierde la información de las dependencias entre variables.
• Observar el rendimiento del modelo para todas las combinaciones de variables posibles. En este sentido, se puede utilizar un algoritmo de búsqueda global estocástica, como los algoritmos genéticos que, si bien pueden ser efectivos, también pueden ser computacionalmente muy costosos.

Los métodos wrapper son de gran eficacia a la hora de eliminar variables irrelevantes y/o redundantes (cosa que no ocurre en los de tipo filtro porque se centran en el poder predictor de cada variable de forma aislada). Además, tienen en cuenta la circunstancia de que dos o más variables, aparentemente irrelevantes en cuanto a su capacidad predictiva o clasificatoria cuando se consideran una por una, pueden ser relevantes cuando se consideran conjuntamente. Sin embargo, son muy lentos, ya que tienen que aplicar muchísimas veces el algoritmo de búsqueda, cambiando cada vez el número de variables, siguiendo cada vez algún criterio tanto de búsqueda como de paro. En lo que respecta a los criterios de búsqueda, estos son similares a los de los métodos tipo filtro. Por lo que se refiere a los criterios de paro, los usados en los métodos wrapper son menos eficientes que los criterios basados en algún tipo de medida de ganancia de información, distancia o consistencia, entre el predictor y la variable objetivo (o clase) que utilizan los de tipo filtro.

Nota

Las principales diferencias entre los métodos tipo filtro y tipo envoltura son las siguientes:

• Los métodos de filtro cuantifican la relevancia de las variables por su correlación con la variable salida, mientras que los métodos de tipo envoltura cuantifican las prestaciones del modelo para diferentes subconjuntos de variables.

• Los métodos de filtro tienen una carga computacional enormemente inferior a la de los envolventes, ya que no necesitan entrenar ningún modelo.

• Los métodos de filtro utilizan métodos estadísticos para evaluar la selección de variables; los de tipo envoltura utilizan métodos de validación cruzada.

• En la mayoría de ocasiones, la selección de variables realizada por los métodos tipo envoltura suele ser más exitosa que la proporcionada por los métodos de filtro.

• Los métodos de envoltura tienen una probabilidad de sobreajuste mucho mayor que los de filtro.

A continuación, sobre el conjunto de datos Madrid_Sale_sample_na y sobre la variable objetivo price_bin se establecen tanto los parámetros de los algoritmos de búsqueda como los métodos de filtrado y se calculan los resultados, usando para ello el paquete FSinR. Como método de selección de variables se utiliza un método wrapper (con la función wrapperEvaluator()de FSinR) y como algoritmo de búsqueda sequential forward selection.

# Se fijan los parámetros
evaluador <- wrapperEvaluator("rpart1SE")
buscador <- searchAlgorithm("sequentialForwardSelection")
# Se evalúan sobre Madrid_Sale_sample_na
results <- featureSelection(Madrid_Sale_sample_na, "price_bin", buscador, evaluador)
resultados$bestFeatures
resultados$bestValue

El resultado es el mismo que con el método tipo filtro anteriormente utilizado: el modelo seleccionado para explicar el comportamiento de la variable objetivo price_bin contiene únicamente el término independiente y una variable predictora: HASTERRACE.

Nota

Se puede sofisticar más el modelo ajustando los parámetros del modelo con parámetros de remuestreo, que son los mismos argumentos que se pasan a la función trainControl() del paquete caret. En segundo lugar, se pueden establecer los parámetros de ajuste, que son los mismos que para la función de train de caret.

9.2.2.3 Métodos de selección tipo intrínseco (embedded)

Finalmente, hay algunos algoritmos de aprendizaje automático que realizan la selección automática de variables como parte del aprendizaje del modelo. Estos son los métodos de selección de tipo intrínseco, que aglutinan las ventajas de los métodos de filtro y envoltura.

Un ejemplo son los relativos a los modelos de regresión penalizados, como Lasso, o ridge (que tienen funciones de penalización incluidas para reducir el sobreajuste), árboles de decisión y bosques aleatorios.

En el siguiente ejemplo se modeliza un bosque aleatorio (usando el paquete randomForest) y, tras dicha modelización, se identifica el conjunto óptimo de variables con la función varImp() de caret.

library("randomForest")

# Usar random forest para la selección de variables
rf_modelo <- randomForest(price_bin ~ ., data = Madrid_Sale_num_sample_bin)

# Listar las variables más importantes
varImp(rf_modelo)

Con este método de selección de variables, el modelo con mayor poder predictivo de la variable salida price_bin es el que contiene un término independiente y los predictores CONSTRUCTEDAREA, ROOMNUMBER y BATHNUMBER (ejecútese el código para comprobarlo).

9.3 Transformación de variables

La transformación y creación de variables predictoras a partir de los datos en bruto tiene un componente técnico y otro más creativo; en este último, son de gran relevancia la intuición y la experiencia en trabajos de modelado, así como el dominio de los datos en cuestión. Para labores de transformación también se utilizará el paquete caret.

Nota

Caret se ha elegido como herramienta principal para la parte de preprocesamiento por su amplia difusión y porque también se utiliza en la parte de machine learning supervisado de este libro. No obstante, se podrían usar otros paquetes, como recipes, incluido en tidymodels. Este tipo de paquetes, comúnmente llamados metapaquetes (meta-packages), permiten agrupar varios programas junto a sus dependencias para su instalación de una vez. Por tanto, un metapaquete permite ahorrar tiempo y esfuerzo a la vez que facilita la implementación de múltiples modelos en paralelo para, posteriormente, vincular sus resultados.

La fase de modelización puede condicionar la fase previa de preparación de datos. Por ejemplo, determinadas técnicas imponen requisitos y expectativas sobre el tipo y forma de las variables predictoras (Boehmke & Greenwell, 2020). Así, podría ser necesario que la variable objetivo tenga una distribución de probabilidad específica, o la eliminación de variables predictoras altamente correlacionadas con otras y/o que no estén fuertemente relacionadas con la variable objetivo.

Generalmente, estas transformaciones son más útiles para algoritmos como los de regresión, métodos basados en instancias (también llamados memory-based learning methods, como k-vecinos más cercanos –KNN– y Learning Vector Quantization –LVQ–), máquinas de vectores de soporte –SVM– y redes neuronales –NN–, que para métodos basados en árboles y reglas.⁷³

9.3.1 Transformación de la distribución de la variable objetivo

Aunque no siempre es necesario, la transformación de la distribución de la variable objetivo puede llevar a una mejora predictiva significativa, especialmente en el caso de modelos paramétricos. Por ejemplo, los modelos de regresión lineal ordinarios asumen que el término de error, y, por consiguiente, la variable objetivo, se distribuyen normalmente. Pero puede ocurrir, por ejemplo, que la variable objetivo tenga valores atípicos y la suposición de normalidad no se cumpla por asimetricidad.

Para simetrizar la distribución de probabilidad de la variable objetivo (mejorando así la dispersión de valores y, a veces, desenmascarando las relaciones lineales y aditivas entre los predictores y el objetivo) se puede usar una transformación logarítmica (entre otras). Para corregir la asimetría positiva de la distribución probabilística de la variable objetivo se suele utilizar una de las dos opciones siguientes:

• Normalizar con una transformación logarítmica, que proporciona buenos resultados en la mayoría de los casos. En la Fig. 9.2, se puede comprobar que, en el ejemplo que se viene arrastrando, una transformación logarítmica normaliza, en gran medida, la distribución de la variable PRICE. Nótese que, si la variable objetivo tiene valores negativos o cero, una transformación logarítmica producirá \(NaN\) y \(- Inf\), respectivamente. Si los valores de respuesta no positivos son pequeños (por ejemplo, entre \(-0.99\) y \(0\)), se puede aplicar una pequeña compensación (por ejemplo, la función log1p() agrega un 1 al valor antes de aplicar la transformación).

respuesta_log <- log(Madrid_Sale$PRICE)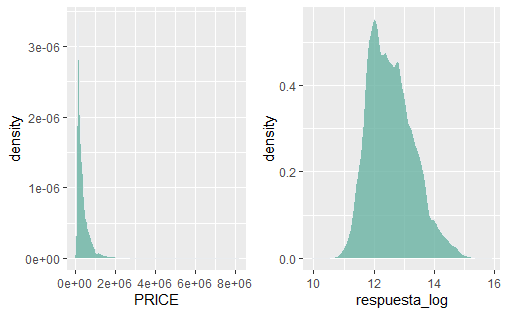

Figura 9.2: Normalización logarítmica.

• Como segunda opción, se puede usar una transformación de la familia de transformaciones Box-Cox (o simplemente una transformación de Box-Cox), de carácter potencial y con mayor flexibilidad que la transformación logarítmica. Generalmente, se puede encontrar la función adecuada a partir de una familia de transformadas de potencia, que llevarán la distribución de la variable transformada tan cerca como sea posible de la distribución normal (Sakia, 1992).⁷⁴ No obstante, igual que la transformación logarítmica, las transformaciones del tipo Box-Cox también tienen la limitación de ser solo aplicables a variables cuyos valores sean positivos. Por consiguiente, tanto si se usa una transformación logarítmica como una Box-Cox, no se deben centrar los datos primero, ni realizar ninguna operación que pueda hacer que los valores de la variable transformada no sean positivos.

• En caso de valores nulos o negativos, una muy buena opción, la tercera, es la transformación Yeo-Johnson, que es una extensión de la transformación Box-Cox que no está limitada a los valores positivos.

respuesta_boxcox <- preProcess(Madrid_Sale_num_sample, method = "BoxCox")
trainBC <- predict(respuesta_boxcox, Madrid_Sale_num_sample)
respuesta_boxcox
#> Created from 5000 samples and 2 variables
#>
#> Pre-processing:
#> - Box-Cox transformation (2)
#> - ignored (0)
#>
#> Lambda estimates for Box-Cox transformation:
#> -0.3, -0.3

Hay que tener en cuenta que, cuando se modela con una variable objetivo transformada, las predicciones también estarán en la escala transformada. Es posible que haya que deshacer (o volver a transformar) los valores pronosticados a su escala original, para que los responsables de la toma de decisiones puedan interpretar los resultados más fácilmente.

Nota

El paquete recipes (recetas de cocina), incluido en tidymodels, permite la transformación de variables de forma secuencial. La transformación de la distribución probabilística de la variable objetivo con recipes se lleva a cabo en 4 etapas: \((i)\) recipe(), donde se especifica la fórmula (variables predictoras y variable objetivo); \((ii)\) step(), donde se definen los pasos a seguir: imputación de valores perdidos, creación de variables ficticias (dummies), normalización, etc.; \((iii)\) prep (preparar, o en otros términos, entrenar), donde se utiliza un conjunto de datos para analizar cada paso en él; y \((iv)\) bake (hornear/cocinar), donde, una vez aplicada la receta, se aplica al conjunto de datos. La idea detrás de recipes es similar a caret::preProcess(). Sin embargo, a diferencia de caret, no maneja automáticamente las variables categóricas y requiere crear variables ficticias manualmente.

9.3.2 Cambios de origen y escala en las variables (normalizaciones)

La escala en que se miden las variables individuales no es una cuestión baladí a la hora de la modelización. Los modelos que incorporan funciones lineales en las variables predictoras son sensibles a la escala de esas variables. Lo mismo puede decirse de los algoritmos que utilizan medidas de distancia, como los de agrupación y clasificación, o los de escalamiento multidimensional, entre otros; o los de reducción de la dimensionalidad. Cuando se estiman modelos, a menudo es aconsejable modificar la escala de las variables predictoras; el objetivo es evitar que unas variables tengan mayor influencia que otras en el resultado obtenido. Por ejemplo, en el conjunto de datos Madrid_Sale la superficie de las viviendas, medida en metros cuadrados, tiene una media y una desviación típica mayores que la antigüedad de la misma, medida en años. En consecuencia, los algoritmos basados en la magnitud de los errores pueden dar más importancia a las variables con mayor desviación típica, pero no porque tengan mayor variabilidad real que las otras, sino porque la medida de dicha variabilidad (la desviación típica) es más grande debido a la distinta escala en la que están medidas dichas variables. La consecuencia: efectos perniciosos indeseados sobre la predicción o la clasificación.

La normalización de variables tiene como objetivo que las comparaciones entre estas variables, en cuanto a su contribución al análisis de interés, sean objetivas; es decir, ponerlas en igualdad de condiciones en lo que respecta a su influencia (más allá de la que realmente tienen) en la variable objetivo.

La estandarización (o normalización z-score) es el método de normalización de variables más popular. Consiste en restar la media de la variable a sus valores y, posteriormente, dividir esta diferencia entre la desviación típica de la variable. De esta manera, las variables (numéricas) transformadas tendrán media nula y varianza unitaria, lo que proporciona una unidad de medida comparable común a todas las variables: la distancia a la media medida en términos de desviaciones típicas.

A modo de ejemplo, a continuación se estandarizan las variables del conjunto de datos Madrid_Sale con la función preProcess() de caret y el method=c('center', 'scale'), de tal manera que su media sea nula y su desviación típica unitaria.

prep_centrado <- preProcess(Madrid_Sale_num, method = c("center","scale"))
pred_centrado<-predict(prep_centrado, Madrid_Sale_num)[1:3]
head(pred_centrado, n = 3)
#>       PRICE    CONSTRUCTEDAREA     ROOMNUMBER
#1    -1.523435    -0.64763050    -0.5764192
#2    -1.523435    -0.38628625    0.4062338
#3    -1.523435    -0.05541004    0.7717038

Otra normalización también popular es la min-max, que reescala los valores de la variable entre 0 y 1, o entre -1 y 1, y cuya expresión general es:

\[X_{norm}=\frac{X-\min(X)}{\max(X)-\min(X)}.\]

Si se desea reescalar entre dos valores arbitrarios, \(a\) y \(b\), la expresión anterior se transforma como sigue:

\[X_{norm}=a+ \frac{(X-\min(X))(b-a)}{\max(X)-\min(X)},\]

Otras opciones de normalización pueden verse en la amplia literatura sobre la cuestión.

Finalmente, conviene recordar que, cuando se lleva a cabo un proceso de normalización de variables, hay que hacerlo tanto en el subconjunto de entrenamiento como en el de test, para que ambos se basen en la misma media y varianza.

9.3.3 Ingeniería de variables (feature engineering)

La ingeniería de variables consiste en el proceso de conseguir, a partir de la información disponible, las variables idóneas (y en el número apropiado) para que los modelos o clasificadores proporcionen los mejores resultados posibles, dados los datos disponibles y el modelo a ejecutar. En otros términos, es el proceso de transformación de las variables seleccionadas, de forma que se obtenga el mejor rendimiento posible de los modelos de machine learning. Por ejemplo, transformar las variables relacionadas con la fecha de tal manera que se diferencie según el tipo de horario (“de oficina” y “de descanso”), o que se considere la cercanía al momento actual (los datos más cercanos contienen más información); los filtros de imagen (desenfocar una imagen) y la conversión de texto en números (utilizando el procesamiento avanzado del lenguaje natural, que asigna palabras a un espacio vectorial) son también ejemplos interesantes.

La mayoría de los modelos requieren que los predictores tengan forma numérica, por lo que, en caso de tener predictores de carácter categórico, hay que transformarlos en numéricos. Para implementar otro tipo de modelos, conviene transformar alguna(s) variable(s) numérica(s) en categórica(s). En el primer caso, conviene aplicar técnicas de agrupamiento (o binning), que crean agrupaciones o intervalos a partir de variables continuas; en el segundo, las técnicas de codificación permiten tratar variables categóricas como si fueran continuas. Hay casos, como el de los modelos basados en árboles, que manejan, de manera natural, variables numéricas y categóricas; pero incluso en estos modelos se puede mejorar su rendimiento si se preprocesan las variables categóricas.

La identificación entre las labores de selección y de transformación de variables es bastante frecuente; sin embargo, es errónea, pues, si bien tienen algunos solapamientos, sus objetivos son claramente distintos. La ingeniería de variables tiene como objetivo la construcción de modelos más sofisticados y más interpretables que los que se pueden implementar con los datos tal y como están en el fichero raíz. La selección de variables permite que el modelo sea manejable, mejorando su interpretabilidad sin que por ello se reduzca significativamente el rendimiento del modelo.

El proceso de agrupamiento ya ha sido referido e ilustrado en la Sec. 9.2.2.1. En cuanto al proceso de codificación, se pueden distinguir dos tipos:

• Codificación de etiquetas: consiste en asignar a cada etiqueta un número entero o valor único según el orden alfabético. Es la codificación más popular y ampliamente utilizada.
• Codificación one-hot: consiste en crear una nueva variable ficticia (dummy) binaria por cada categoría existente en la variable a codificar. Estas nuevas variables contendrán un \(1\) en aquellas observaciones que pertenezcan a esa categoría, y un 0 en el resto.⁷⁵

Para ejemplificar este tipo de codificación, a continuación, en el conjunto de datos Madrid_Sale_num_sample_bin, se crean dummies, una para cada cada categoría de las variables objeto de codificación. Para ello, se utiliza la función dummyVars() de caret. El resultado puede verse con la función predict().

dummies <- dummyVars("  ~ .", data = Madrid_Sale_num_sample_bin)
head(predict(dummies, newdata = Madrid_Sale_num_sample_bin))

No debe olvidarse, igual que para todas las transformaciones descritas, hacer las mismas transformaciones en el conjunto de test.

9.4 Reducción de dimensionalidad

La reducción de dimensionalidad es un enfoque alternativo para filtrar las variables no informativas sin eliminarlas (como se hacía en la Sec. 9.2, que generalmente se usa para variables numéricas). La diferencia es que las técnicas de reducción de la dimensionalidad crean una proyección de los datos que da como resultado variables predictoras completamente nuevas, que son combinaciones lineales independientes formadas a partir de las variables originales, solucionando así, también, los problemas de colinealidad y multicolinealidad (perfecta o cuasiperfecta). Como se explica en el Cap. 32, el espacio de un conjunto de variables puede reducirse proyectándolo a un subespacio de variables de menor dimensión utilizando componentes principales (la técnica de reducción de la dimensionalidad por antonomasia).

Resumen

• Se presentan las principales técnicas y métodos de feature selection para llevar a cabo la selección (preselección y selección propiamente dicha) de las variables predictoras o clasificadoras más relevantes para obtener predicciones o clasificaciones exitosas.

• Se describen las principales transformaciones que se realizan en la fase de preprocesamiento de un proyecto de modelado predictivo: las transformaciones de la escala o de la distribución de la variable objetivo, la transformación de variables (feature engineering) y la reducción de la dimensionalidad.

• La creación de variables predictoras a partir de los datos en bruto tiene un componente creativo, que requiere de herramientas adecuadas y de experiencia para encontrar las mejores representaciones, apoyándose, en la medida de lo posible en el conocimiento que se tenga de los datos.

• Las labores de selección y transformación de variables se ilustran con el conjunto de datos de Madrid_Sale, utilizándose los paquetes caret y rsample.