Capítulo 27 Naive Bayes
Ramón A. Carrasco\(^{a}\), Itzcóatl Bueno\(^{b, \hspace{0,05cm}a}\) y José-María Montero\(^{c}\)
\(^{a}\)Universidad Complutense de Madrid
\(^{b}\)Instituto Nacional de Estadística
\(^{c}\)Universidad de Castilla-La Mancha
27.1 Introducción
Naive Bayes (NB) es un algoritmo de aprendizaje supervisado que se utiliza principalmente para la clasificación.193
Como otros algoritmos de aprendizaje supervisado, se entrena con un conjunto de observaciones que incluye los valores de las \(p\) variables de entrada y de las categorías de la variable respuesta correspondientes a dichas observaciones. Una vez entrenado el algoritmo, se utiliza para predecir la categoría de la variable respuesta que le corresponde a un conjunto de valores de las variables predictoras. La primera palabra del algoritmo, naive, responde al hecho de que asume que las variables de entrada son independientes entre sí, por lo cual si se quitan, se introducen o se cambian algunas variables predictoras, los cálculos en los que están involucrados las demás no se ven afectados. La segunda se debe a que su piedra angular es el teorema de Bayes.
Aunque el algoritmo NB es sencillo y de fácil implementación, destaca por su potencia predictiva. Su principal ventaja es que utiliza un enfoque probabilístico, lo que implica que todos los cálculos se realizan en tiempo real y, por tanto, los resultados se obtienen inmediatamente. Cuando se trabaja con conjuntos de datos pequeños, la ventaja de NB respecto a algoritmos como SVM (Cap. 25), random forest (Cap. 28) o boosting (Cap. 29). Sin embargo, cuando el tamaño del conjunto de datos es pequeño, esta ventaja se reduce notablemente, pues en ese caso la optimización de estos últimos algoritmos no es tan exigente, y la ventaja en tiempo de computación del NB podría no compensar la pérdida en capacidad predictiva.
Los conceptos probabilísticos necesarios para entender el funcionamiento del algoritmo NB pueden verse en el Cap. 12. No obstante, a continuación se muestra un brevísimo repaso del teorema de Bayes, que es la base del algoritmo.
27.2 Teorema de Bayes
Sean dos sucesos \(A\) y \(B\) definidos en un espacio muestral. Se define la probabilidad condicional de que ocurra el suceso \(A\) dado que previamente se haya observado \(B\) como:
\[\begin{equation} P(A|B) = \frac{P(A\cap B)}{P(B)}, \end{equation}\]
donde \(P(B) \neq 0\) y \(P(A\cap B)\) es la probabilidad de que ocurran ambos eventos a la vez. Los sucesos son intercambiables, de tal forma que:
\[\begin{equation} P(B|A) = \frac{P(B\cap A)} {P(A)}, \text{\hspace{0,1cm}lo\hspace{0,1cm} que\hspace{0,1cm} \hspace{0,1cm}implica\hspace{0,1cm} que\hspace{0,1cm}} P(A\cap B) = P(A)P(B|A), \end{equation}\]
con lo que:
\[\begin{equation} P(A|B) = \frac{P(A)\cdot P(B|A)}{P(B)}. \end{equation}\]
Y si \(A_1,A_2,...,A_k\) forman una partición de \(A\), las denominadas alternativas, se tiene que:
\[\begin{equation} P(A_m|B) = \frac {P(A_m) P(B|A_m)}{\sum_{i=1}^{k} P(A_m) P(B|{A_m})}. \end{equation}\]
Esta expresión es conocida como teorema de Bayes. Para ampliar los conceptos probabilísticos aquí presentados puede consultarse el Cap. 12.
27.3 El algoritmo Naive Bayes
Supóngase un conjunto de datos con \(p\) variables predictoras, \(X_1,X_2,...,X_p\), y una variable respuesta con \(k\) clases, \(c_1, c_2,...,c_k\). Considérese el caso, instancia u observación \({\bf{x}}^{\prime}_j=(x_1, x_2,...,x_p), \hspace{0,2cm} j=1,2,...,N\). Entonces, la adaptación del teorema de Bayes para aplicarlo a un problema de clasificación es como sigue: se trata de calcular la probabilidad de que, dada una observación, \({\bf{x}}_j\), esta pertenezca a una determinada clase de la variable respuesta, por ejemplo la m-ésima clase, \(c_m\), de tal manera que dicha observación se asignará a la clase para la que se obtenga una mayor probabilidad:
\[\begin{equation} P(C=c_m|{\bf{x}}_j)=\frac{P(C=c_m) \cdot P({\bf{x}}_j|C=c_m)}{P({\bf{x}}_j)}, \end{equation}\]
donde, en la jerga bayesiana:
\(P(C=c_m), \hspace{0,1cm} i=1,...m, ...,k\), se denominan probabilidades a priori y son las probabilidades de que una observación o instancia, de la que no se conocen los valores de sus características, pertenezca (y, por tanto, sea asignada) a cada una de las clases de la variable respuesta.
\(P({\bf{x}}_j|C=c_m)\) son las probabilidades de que una observación o instancia, \({\bf{x}}_j\), sea asignada a cada una de las clases de la variable respuesta, pero, esta vez, conociéndose los valores de sus características. Se denominan verosimilitudes.
\(P({\bf{x}}_j)\) es la probabilidad de observar una instancia particular, \(P(C=c_m|{\bf{x}}_j)\), independientemente de a qué clase pertenezca el individuo.
\(P(C=c_m|{\bf{x}}_j)\) son las probabilidades de que, dado un vector de características concreto, \({\bf{x}}_j\), el elemento al que pertenezcan sea clasificado en la clase m-ésima de la variable respuesta (\(m=1,2,...,k\)). Se conocen como probabilidades a posteriori porque se calculan a posteriori a partir de las probabilidades a priori y las verosimilitudes haciendo uso del teorema de Bayes.
Sin embargo, a la hora de computar las denominadas probabilidades a posteriori, surge una dificultad: el cálculo de las verosimilitudes \(P({\bf{x}}_j|C=c_m)= P(X_1=x_1\cap X_2=x_2\cap\dots\cap X_p=x_p|C=c_m)\) (consúltese el Cap. 12 para ver de forma específica su cálculo). En primer lugar, puede que en el conjunto de datos no exista ningún caso en el que las variables predictoras tomen precisamente los valores \(X_1=x_1; X_2=x_2,..., X_p=x_p\). En segundo lugar, en caso de existir, el número de ellos podría no ser suficiente para estimar con una mínima fiabilidad la probabilidad de pertenencia a cada una de las clases de la variable respuesta.
La forma como el algoritmo KNN supera esta limitación es adoptar el supuesto de que las variables predictoras son independientes. Este supuesto, sin duda, es un supuesto muy fuerte y, de ahí, que la denominación de ingenuo (naive) que recibe el algoritmo.
Dos sucesos \(A\) y \(B\) son condicionalmente independientes dado un tercero, \(C\), si:
\[\begin{equation} P(AB|C) = P(A|C)\cdot P(B|C). \end{equation}\]
Por consiguiente, la suposición naive de que las variables o características predictoras de los elementos que conforman el conjunto de datos disponible son independientes, lleva a que:
\[\begin{equation} \label{nb-eq1} \begin{split} P({\bf{x}}_j|C=c_m) & = P(X_1=x_1 \cap X_2=x_2\cap \dots\cap X_p = x_p|C=c_m) \\ & = P(X_1=x_1|C=c_m) \cdot P(X_2=x_2|C=c_m) \cdots P(X_p=x_p|C=c_m), \end{split} \end{equation}\] donde cada uno de los términos \(P(X_j=x_j|C=c_m), \hspace{0,2cm} j=1,...,p\), puede obtenerse directamente de los datos.
Por tanto,
\[\begin{equation} \label{nb-eq2} \begin{split} P(C=c_m|{\bf{x}}_j) & =\frac{P(C=c_m) \cdot P(X_1=x_1 \cap X_2=x_2\cap \dots\cap X_p = x_p|C=c_m)} {P({\bf{x}}_j)} \\ & =\frac{P(C=c_m) \cdot P(X_1=x_1|C=c_m) \cdot P(X_2=x_2|C=c_m) \cdots P(X_p=x_p|C=c_m)} {P({\bf{x}}_j)}. \end{split} \end{equation}\]
Y, como sea cual sea la clase \(c_m\) el denominador de la expresión anterior es el mismo, se tiene finalmente que la ecuación de decisión del algoritmo NB es:
\[\begin{equation} P(C=c_m) \cdot P(X_1=x_1|C=c_m) \cdot P(X_2=x_2|C=c_m) \cdot P(X_p=x_p|C=c_m), \end{equation}\]
de tal manera que a cada nueva observación, \({\bf{x}}_j\), se le asigna a la clase con mayor \(P(C=c_m|{\bf{x}}_j)\).
En definitiva, el clasificador NB es muy eficiente en términos de espacio de almacenamiento y tiempos de procesamiento. Además, a pesar de ser muy simple, tiene en cuenta las características observadas. Otra de las ventajas de este clasificador es su aprendizaje incremental; es decir, es una técnica de inducción que se actualiza con cada nueva observación de entrenamiento, por lo que no es necesario volver a procesar todo el conjunto de entrenamiento cuando se dispone de nuevas observaciones.
Para ilustrar los anteriores conceptos, considérese de nuevo el ejemplo presentado en el Cap. 24, en el que se trata de predecir si se puede jugar o no al tenis con unas condiciones meteorológicas determinadas. La variable respuesta es, por tanto, Si un determinado día se juega al tenis, con dos categorías: \(c_1=SÍ\) y \(c_2=NO\). Las variables (en este caso factores) predictoras son \(X_1=Tipo \hspace{0,1cm} de \hspace{0,1cm}día\), con tres categorías: soleado, nublado y con lluvia, \(X_2=Humedad\), con dos categorías: fuerte y débil, y \(X_3=Fuerza \hspace{0,1cm} del \hspace{0,1cm} viento\), también con dos categorías: fuerte y débil. En cuanto a la regla de decisión, por ejemplo, para un día soleado con humedad fuerte y fuerza del viento débil, sería:
Se juega si: \[\begin{equation*} \begin{split} & P\left(Jugar=\textit {SÍ})| ( X_1= soleado; X_2= fuerte; X_3= débil \right) = \\ & P(Jugar=\textit {SÍ}) \cdot P(X_1= soleado |Jugar=\textit {SÍ}) \cdot \\ & \cdot P(X_2= fuerte|Jugar=\textit {SÍ}) \cdot P(X_3= débil|Jugar=\textit {SÍ}) \end{split} \end{equation*}\]
es mayor que:
\[\begin{equation*} \begin{split} & P\left(Jugar={NO}| ( X_1= soleado; X_2= fuerte; X_3= débil \right) = \\ & P(Jugar={NO}) \cdot P(X_1= soleado |Jugar={NO}) \cdot \\ & \cdot P(X_2= fuerte|Jugar={NO}) \cdot P(X_3= débil|Jugar={NO}). \end{split} \end{equation*}\]
Lo mismo se haría para decidir si se juega o no con cualquier otra combinación de categorías de la variables \(X_1\), \(X_2\) y \(X_3\).
Siguiendo con el ejemplo de un día soleado, con humedad fuerte y fuerza del viento débil, los pasos a seguir para determinar si se juega o no al tenis serían los tres siguientes:194
- Organizar los datos en tablas de frecuencias de dos dimensiones, tantas como variables predictoras. Una de las dimensiones corresponde a una de las variables predictoras y la otra, a la variable respuesta.
- Calcular, a partir de la tablas anteriores, las probabilidades a priori y las verosimilitudes.
- Aplicar el teorema de Bayes para calcular las probabilidades a posteriori y realizar la predicción.
Particularizando en el caso anteriormente referido en las Tablas 27.1, 27.2 y 27.3 (día soleado con humedad fuerte y viento débil), las 15 observaciones registradas se presentan en la Tabla 27.1 (una tabla de contingencia (3 x 2), usando la terminología del Cap. 23), donde uno de los factores es el primer factor explicativo, \(X_1\), Tipo de día, con tres categorías (soleado, nublado, lluvioso) y el otro es Si ese día se jugó, con dos categorías: SÍ y NO.
| \(X_1\) | SÍ | NO | Total |
|---|---|---|---|
| Soleado | 2 | 4 | 6 |
| Nublado | 4 | 0 | 4 |
| Lluvia | 4 | 1 | 5 |
| Total | 10 | 5 | 15 |
| \(X_2\) | SÍ | NO | Total |
|---|---|---|---|
| Débil | 6 | 2 | 8 |
| Fuerte | 4 | 3 | 7 |
| Total | 10 | 5 | 15 |
| \(X_3\) | SÍ | NO | Total |
|---|---|---|---|
| Débil | 6 | 1 | 7 |
| Fuerte | 4 | 4 | 8 |
| Total | 10 | 5 | 15 |
En un segundo paso, a partir de cualquiera de las tablas anteriores se obtienen las probabilidades a priori de clasificar una observación en una u otra categoría de la variable respuesta (SÍ, NO). Por ejemplo, en la Tabla 27.4 aparecen al final de las columnas SÍ y NO.
| SÍ | NO | \(P(\textrm{Tipo de día}_i)\) | |
|---|---|---|---|
| Soleado | 2 | 4 | \(\frac{6}{15} = \text{0,40}\) |
| Nublado | 4 | 0 | \(\frac{4}{15} = \text{0,27}\) |
| Lluvia | 4 | 1 | \(\frac{5}{15} = \text{0,33}\) |
| \(P\)(Jugar) | \(\frac{10}{15} = \text{0,67}\) | \(\frac{5}{15} = \text{0,33}\) | – |
También a partir de ellas se obtienen las verosimilitudes de cada categoría de los tres factores dada una categoría de la variable respuesta (se jugó; no se jugó).
A partir de la Tabla 27.4 se obtiene la probabilidad de cada tipo de día dado que con esa climatología se jugó o no, es decir, \(P(\textrm{Tipo de día}|Jugar)\), obteniendo las probabilidades mostradas en la Tabla 27.5.
| \(X_1\) | \(c_1\) = SÍ | \(c_2\) = NO |
|---|---|---|
| \(P\)(Soleado | \(C=c_m\)) | \(\frac{2}{10}\) | \(\frac{4}{5}\) |
| \(P\)(Nublado | \(C=c_m\)) | \(\frac{4}{10}\) | \(\frac{0}{5}\) |
| \(P\)(Lluvia | \(C=c_m\)) | \(\frac{4}{10}\) | \(\frac{1}{5}\) |
| \(X_2\) | \(c_1\) = SÍ | \(c_2\) = NO |
|---|---|---|
| \(P\)(Débil | \(C=c_m\))) | \(\frac{6}{15}\) | \(\frac{1}{15}\) |
| \(P\)(Fuerte | \(C=c_m\)) | \(\frac{4}{15}\) | \(\frac{4}{15}\) |
| \(X_3\) | \(c_1\) = SÍ | \(c_2\) = NO |
|---|---|---|
| \(P\)(Débil | \(C=c_m\))) | \(\frac{6}{15}\) | \(\frac{2}{15}\) |
| \(P\)(Fuerte | \(C=c_m\))) | \(\frac{4}{15}\) | \(\frac{3}{15}\) |
A partir de las probabilidades previamente obtenidas (Tablas 27.5, 27.6 y 27.7) y de la asunción de independencia entre las variables, se puede calcular la probabilidad de jugar, dadas las condiciones meteorológicas expuestas, como:
\[\begin{equation} \begin{split} P(\textit {SÍ}|X_1:soleado, X_2: fuerte, X_3: débil) = \\ P(\textit {SÍ}) \cdot P(Soleado|\textit {SÍ}) \cdot P(Fuerte|\textit {SÍ}) \cdot P (Débil|\textit {SÍ}) = \\ \frac{10}{15}\cdot \frac{2}{10}\cdot \frac{4}{10}\cdot \frac{6}{10} = \text{0,0320}. \end{split} \end{equation}\]
\[\begin{equation} \begin{split} P(NO|X_1: soleado, X_2: fuerte, X_3: débil) = \\ P(NO) \cdot P(Soleado|NO) \cdot P(Fuerte|NO) \cdot P (Débil|NO) = \\ \frac{5}{15}\cdot \frac{4}{5}\cdot \frac{4}{5}\cdot \frac{2}{5} = \text{0,0853}. \end{split} \end{equation}\]
La probabilidad de no jugar es superior a la probabilidad de jugar y, por tanto, dado un día con esas condiciones climáticas se clasificará como un día en el que no se puede jugar.
Igual que se ha procedido con esta predicción para un día soleado con fuerte humedad y fuerza del viento débil, se procede para cualquier combinación de las categorías de los factores predictores.
27.4 Procedimiento con R: la función naive_bayes()
Para entrenar el algoritmo NB se utiliza la función naive_bayes() del paquete naivebayes.
naive_bayes(formula, data, prior = ..., ...)-
formula: refleja la relación lineal entre la variable respuesta y los predictores: \(Y \sim X_1 + ... + X_p\). -
data: conjunto de datos con el que se entrena el modelo. -
prior: vector con las probabilidades a priori de las clases.
27.5 Clasificación de clientes utilizando el modelo Naive Bayes
Como en los capítulos precedentes, para ejemplificar el uso del algoritmo NB se utiliza de nuevo el conjunto de datos dp_entr, incluido en el paquete CDR, que contiene una serie de variables predictoras relativas a los productos que han comprado previamente los clientes de una empresa, el importe que han gastado y otras características como su edad y su nivel educativo. Dicho conjunto se utiliza con los datos sin transformar, es decir, en su escala original y con las variables categóricas sin codificar. La variable objetivo indica si un cliente comprará o no el nuevo producto (tensiómetro digital).
library("caret")
library("naivebayes")
library("reshape")
library("ggplot2")
library("CDR")
data("dp_entr")
# se fija la semilla aleatoria
set.seed(101)
# se entrena el modelo
model <- train(CLS_PRO_pro13 ~ .,
data=dp_entr,
method="nb",
metric="Accuracy",
trControl=trainControl(classProbs = TRUE,
method = "cv",
number = 10))# se muestra la salida del modelo
model
Naive Bayes
558 samples
17 predictor
2 classes: 'S', 'N'
No pre-processing
Resampling: Cross-Validated (10 fold)
Summary of sample sizes: 502, 502, 502, 503, 503, 502, ...
Resampling results across tuning parameters:
usekernel Accuracy Kappa
FALSE 0.8512662 0.7026716
TRUE 0.8512338 0.7025165
Tuning parameter 'fL' was held constant at a value of 0
Tuning parameter
'adjust' was held constant at a value of 1
Accuracy was used to select the optimal model using the largest value.
The final values used for the model were fL = 0, usekernel = FALSE and adjust = 1.Los resultados del proceso de entrenamiento muestran que, en este caso, es indiferente indicar el argumento usekernel como FALSE o TRUE, pues los resultados de la medida de accuracy (proporción de predicciones correctas) son similares.195 196 197
confusionMatrix(model)Cross-Validated (10 fold) Confusion Matrix
(entries are percentual average cell counts across resamples)
Reference
Prediction S N
S 41.8 6.6
N 8.2 43.4
Accuracy (average) : 0.8513En la matriz de confusión del modelo se proporciona en cada celda el promedio porcentual en los distintos remuestreos. Así, se observa que, en media, el modelo predice mejor cuando un cliente no va a comprar el nuevo producto que cuando sí lo hace, aunque no con mucha diferencia (menos de un 2%). En ambos casos, las clasificaciones erróneas no suponen ni el 10%.
ggplot(melt(model$resample[,-4]), aes(x = variable, y = value, fill=variable)) +
geom_boxplot(show.legend=FALSE) +
xlab(NULL) + ylab(NULL)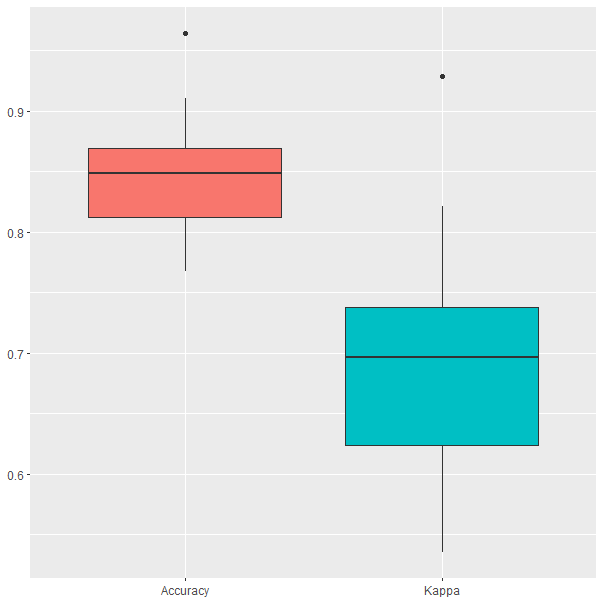
Figura 27.1: Resultados del modelo Naive Bayes obtenidos durante el proceso de validación cruzada.
En la Fig. 27.1 se puede observar que la accuracy oscila entre el 75% y el 95% en el proceso de validación cruzada, aunque en uno de los resultados se obtuvo un 96%, que aparece marcado como un outlier. La kappa de Cohen oscila entre el 63% y el 82%, con un outlier en el 82%.