Capítulo 35 Análisis de correspondencias

Román Mínguez Salido\(^{a}\) y Manuel Vargas Vargas\(^{a}\)

\(^{a}\)Universidad de Castilla-La Mancha

35.1 Introducción

El análisis de correspondencias es un método gráfico descriptivo de reducción de la dimensión incluido entre los algoritmos de aprendizaje no supervisado. La idea principal es equivalente al método de componentes principales, pero aplicado a variables cualitativas. El objetivo es representar los valores (niveles en R) de variables cualitativas (factores en R) en ejes cuantitativos cuyas coordenadas representen la cercanía o lejanía entre los niveles de los factores. Es decir, es un método de reducción de la dimensionalidad para factores representables en pocas dimensiones.

Por sencillez, el punto de partida será una tabla de contingencia \(R \times C\) (véase Cap. 23) con dos factores \(A\) y \(B\) cuyos niveles son \(A_1,A_2,...,A_R\) y \(B_1,B_2,...,B_C\), respectivamente, que recoge la frecuencia de las distintas combinaciones que se pueden llevar a cabo con los niveles de \(A\) y \(B\), como se muestra en la Tabla 35.1.

Tabla 35.1: Ejemplo de tabla de contingencia \(R \times C\)
	\(B_1\)	\(B_2\)	…	\(B_C\)	Total
\(A_1\)	\(n_{11}\)	\(n_{12}\)	…	\(n_{1C}\)	\(n_{1.}\)
\(A_2\)	\(n_{21}\)	\(n_{22}\)	…	\(n_{2C}\)	\(n_{2.}\)
…	…	…	…	…	…
\(A_R\)	\(n_{R1}\)	\(n_{R2}\)	…	\(n_{RC}\)	\(n_{R.}\)
Total	\(n_{.1}\)	\(n_{.2}\)	…	\(n_{.C}\)	\(N\)

Cada fila representa el perfil condicional del nivel \(A_i\), siendo la última el perfil marginal del factor \(A\). Igualmente, cada columna representa el perfil condicional del nivel \(B_j\), siendo la última el perfil marginal del factor \(B\).

Como se vio en el Cap. 23, si los factores son independientes, el valor esperado en cada casilla sería \(E_{ij}=\frac{n_{i.}n_{.j}}{N}\), por lo que la diferencia tipificada, \(r_{ij}=\frac{n_{ij}- E_{ij}}{\sqrt{E_{ij}}}\) es una medida de asociación entre las modalidades \(A_i\) y \(B_j\). La matriz formada por estos “residuos estandarizados” (véase Sec. 23.5), \({\bf R}_{est}=\lbrace r_{ij} \rbrace\), que resume la asociación entre los atributos, es el objetivo básico del análisis de correspondencias; básicamente, se realiza una proyección de las filas y columnas de la tabla de frecuencias relativas (proyecciones también denominadas transformadas de las frecuencias relativas) para obtener las coordenadas en ejes cuantitativos, coordenadas representables en la forma habitual como diagramas de puntos.

Para un estudio en profundidad de esta técnica pueden consultarse, entre otros, Greenacre (2008) (en español) o Beh & Lombardo (2014). En el resto del capítulo se hará una breve exposición de la metodología y se ejemplificará con el análisis de dos tablas de contingencia.

35.2 Metodología del análisis de correspondencias

Dada una tabla de contingencia, a partir de las frecuencias observadas \(n_{ij}\), se definen las distancias entre los perfiles:

Para los perfiles fila, \(d_{ii^\prime}= \sum_{j=1}^C \frac {1}{n_{.j}} \left( \frac {n_{ij}}{n_{i.}} - \frac {n_{i^\prime j}}{n_{i^\prime.}} \right)^2.\)
Para los perfiles columna, \(d_{jj^\prime}= \sum_{i=1}^R \frac {1}{n_{i.}} \left( \frac {n_{ij}}{n_{.j}} - \frac {n_{ij^\prime}}{n_{.j^\prime}} \right)^2.\)

Cuanto más se “diferencien” unos perfiles de otros, más grandes serán las anteriores diferencias. El análisis de correspondencias busca construir dimensiones (habitualmente, dos) y obtener las coordenadas de los niveles de ambos factores en dichas dimensiones:

\[\begin{equation} \textbf{A} = \left( {\textbf{a} }_1 \hspace{0,1cm}{\textbf{a} }_2\\ \dots\\ {\textbf{a}_R }\right) \text{, con } {\bf a}_i= \begin{pmatrix} {a_{i1} }\\ {a_{i2} } \end{pmatrix} \text{, y } \textbf{B} = \left( {\textbf{b} }_1 \hspace{0,1cm} {\textbf{b} }_2\\ \dots\\ {\textbf{b}_C }\right) \text{, con } \textbf{b}_j = \begin{pmatrix} {{b}_{j1}}\\ {{b}_{j2}}\end{pmatrix}, \end{equation}\]

siendo \(\textbf{a}_i\) las coordenadas del nivel fila \(A_i\) y \(\textbf{b}_j\) las del nivel columna \(B_j\) en el plano, de forma que “reproduzcan” las distancias entre perfiles fila y columna y los residuos estandarizados (asociaciones):

\[\begin{equation} \begin{array}{crl} {d(\textbf{a}_i , \textbf{a}_{i'})= \sqrt {(a_{i1}-a_{i'1})^2+(a_{i2}-a_{i'2})^2} \approx d_{ii'}}, \\ {d(\textbf{b}_j , \textbf{b}_{j'})= \sqrt {(b_{j1}-b_{j'1})^2+(b_{j2}-b_{j'2})^2} \approx d_{jj'}}, \\ {\bf a}_{i}^{\prime} \textbf{b}_j \approx r_{ij}. \end{array} \end{equation}\]

Una vez en disposición de las coordenadas contenidas en las matrices \(\bf A\) y \(\bf B\) es posible “visualizar” la posición relativa de cada factor en las nuevas dimensiones. Esta estructura permite ver tanto las “distancias” que hay entre los niveles de cada factor (mediante la distancia de representación en el plano) como las “asociaciones” entre niveles de ambos factores (ya que mientras más asociación haya, más cerca se representarán en el plano).

Para resolver el problema de la estimación de las matrices \(\bf A\) y \(\bf B\) se lleva a cabo una descomposición de la matriz de \(\textbf{R}= \lbrace r_{ij} \rbrace\) en valores singulares.

Según la importancia que se dé al ajuste de uno de los perfiles o a la matriz de residuos, se tienen diferentes métodos de selección, llamados normalizaciones, que pueden consultarse en Greenacre (2008).

35.2.1 Proyecciones fila, columna y simétrica

El punto de partida es la matriz de frecuencias relativas \(\bf{F}\), cuyas entradas son \(f_{ij}=n_{ij}/N\), también llamada matriz de correspondencias. Definiendo el vector de unos, \(\mathbf{1}\), con la dimensión adecuada, las masas, o frecuencias marginales, de filas y columnas, \(r_i=f_{i.} = \sum_{j=1}^C f_{ij}\) y \(c_{.j}=f_{.j} = \sum_{i=1}^R f_{ij}\), respectivamente, se pueden expresar matricialmente como \(\textbf{r}=\textbf{F} \mathbf{1}\) y \(\bf c=\textbf{F}^{\prime} \mathbf{1}\) o, en forma de matrices diagonales, como: \[\textbf{D}_R=diag(r) \equiv diag(r_{1},...,r_{R}) \text{ y } \ \textbf{D}_C=diag(c) \equiv diag(c_{1},...,c_{C}).\]

Se calcula la matriz de residuos estandarizados (véanse Sec. 23.3.1 y Cap. 23) como:

\[\begin{equation} {\textbf{R}}_{est}=\textbf{D}_R^{-\frac {1}{2}} \left(\textbf{F}-\textbf{r}{\textbf{c}}^{\prime}\right) \textbf{D}_C^{-\frac {1}{2}}. \end{equation}\]

La matriz \({\bf R}_{est}\) se descompone en valores singulares, calculando las matrices \(\bf U\), \(\bf D\) y \(\bf V\) tales que:

\[\begin{equation} \begin{array}{crl} \textbf{R=UDV}^{\prime}, \\ \textbf{UU}^{\prime} = \textbf V^{\prime} \textbf {V}=\textbf{I}, \hspace{0,5cm} \textbf{U}_{(RxK)}, \hspace{0,5cm} \textbf{V}_{(CxK)}, \hspace{0,5cm} \ K=min(R-1, C-1), \\ {\textbf{D}=diag(\mu_1,...,\mu_K)}, \end{array} \end{equation}\]

donde los \(\mu_i\) son los llamados valores singulares (o autovectores), estando ordenados de forma decreciente \(\mu_1 \geq \mu_2 \geq ... \geq \mu_K\).

A partir de esta descomposición se pueden obtener:

Las coordenadas estándar de las filas, \({\Phi}=\textbf{D}_R^{-\frac {1}{2}}\textbf{U}\), y sus coordenadas principales, \(\textbf{H}=\Phi \textbf{D}\).
Las coordenadas estándar de las columnas, \({\Gamma}=\textbf{D}_C^{-\frac {1}{2}}\textbf{V}\), y sus coordenadas principales, \(\textbf{G}=\Gamma \textbf{D}\).
Las inercias principales, \(\lambda_i=\mu_i^2\).

Las coordenadas estándar permiten representar los perfiles en un plano, pero no permiten una comparación fácil entre perfiles fila y columna. Para evitar este efecto, se escalan, dando lugar a las coordenadas principales, utilizadas para definir las proyecciones fila y proyecciones columna, que representan los correspondientes perfiles, formando los llamados mapas asimétricos. Las inercias principales indican el grado de variabilidad entre los perfiles fila o columna y los respectivos vectores de medias, por lo que tienen una interpretación equivalente a la variabilidad explicada por cada componente principal en el análisis de componentes principales (véase Cap. 32).

Por último, las matrices \(\textbf{A}=\textbf{D}_R^{-\frac {1}{2}} \textbf{UD}\) y \(\textbf{B}=\textbf{D}_C^{-\frac {1}{2}} \textbf{VD}\) representan las coordenadas de ambos perfiles en un espacio común, llamado mapa simétrico.

35.3 Procedimiento con R: la función `ca()`

Para realizar un análisis de correspondencias simple con el software R se puede utilizar el paquete ca, que contiene la función ca(). Esta función acepta como argumento de entrada o bien directamente una tabla de contingencia, o bien los datos originales como objeto matriz o dataframe. Incluso, el argumento puede ser una fórmula del tipo ~ \(F_1 + F_2\) donde \(F_1\) y \(F_2\) son factores. Entre los argumentos adicionales se pueden incluir el número de dimensiones en el output, así como filas o columnas suplementarias.

35.3.1 Caso práctico 1: tareas del hogar

Como primer ejemplo se utilizan los datos housetasks, contenidos en el paquete factoextra, que están en forma de tabla de contingencia que contiene la frecuencia de ejecución de 13 tareas del hogar por los miembros de la pareja.

library("ca")
library("factoextra")
data("housetasks")

En primer lugar, la aplicación del test \(\chi^2\) de independencia (véase Cap. 23) permite contrastar si los factores son independientes o, por el contrario, están asociados:

chisq.test(housetasks)
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  housetasks
#> X-squared = 1944.5, df = 36, p-value < 2.2e-16

Dado que \(\chi^2 =1944.5\) y el p-valor es de 2.2e-16, hay suficiente evidencia como para rechazar la hipótesis nula de independencia en favor de la asociación entre ambos factores, por lo que tiene sentido analizar más en profundidad la estructura de dicha asociación.

La función ca() proporciona:

Los valores singulares y, tanto para filas como para columnas, las masas (valores Mass);
las distancias Chi-cuadrado, que representan las distancias en esa métrica de cada fila respecto a la fila centroide (dada por la masa de las columnas, promedio de los vectores fila);
las inercias principales, que representan la distancia cuadrática \(\chi^2\) respecto al perfil promedio (sin calcular raíces), ponderada por la masa (de la fila o columna) correspondiente;
las coordenadas estándar en el espacio proyectado.²⁴⁵

Dichos resultados pueden verse en la salida siguiente:

options(digits = 2)
ca_house <- ca(housetasks, nd = 2)
ca_house
#> 
#>  Principal inertias (eigenvalues):
#>            1        2        3       
#> Value      0.542889 0.445003 0.127048
#> Percentage 48.69%   39.91%   11.4%   
#> 
#> 
#>  Rows:
#>         Laundry Main_meal Dinner Breakfeast Tidying Dishes Shopping Official
#> Mass       0.10     0.088  0.062      0.080   0.070  0.065    0.069    0.055
#> ChiDist    1.15     1.017  0.786      0.716   0.594  0.550    0.466    0.984
#> Inertia    0.13     0.091  0.038      0.041   0.025  0.020    0.015    0.053
#> Dim. 1    -1.35    -1.188 -0.940     -0.690  -0.534 -0.256   -0.160    0.308
#> Dim. 2    -0.74    -0.735 -0.462     -0.679   0.651  0.663    0.605   -0.380
#>         Driving Finances Insurance Repairs Holidays
#> Mass       0.08    0.065     0.080   0.095    0.092
#> ChiDist    1.13    0.675     0.853   1.819    1.463
#> Inertia    0.10    0.030     0.058   0.313    0.196
#> Dim. 1     1.01    0.367     0.878   2.075    0.343
#> Dim. 2    -0.98    0.926     0.710  -1.296    2.151
#> 
#> 
#>  Columns:
#>          Wife Alternating Husband Jointly
#> Mass     0.34       0.146    0.22    0.29
#> ChiDist  0.94       0.899    1.32    1.04
#> Inertia  0.30       0.118    0.38    0.31
#> Dim. 1  -1.14      -0.084    1.58    0.20
#> Dim. 2  -0.55      -0.437   -0.90    1.54

Como puede apreciarse en la salida anterior, las dos primeras dimensiones explican el 48,69 % y 39,91 % de la inercia, respectivamente, por lo que la representación en un plano engloba al 88,6 % de la inercia total. Es decir, se está recogiendo en dos dimensiones el 88,6 % de la variabilidad general entre los perfiles fila y columna y sus respectivos vectores de medias.

Las distancias Chi-cuadrado indican lo cerca o lejos que está cada fila respecto al centroide de las mismas. En este ejemplo, la fila más distante del centroide de filas es Repairs (1,819), mientras que la columna más distante respecto del centroide de columnas es Husband (1,321).

En cuanto a las inercias (autovectores; miden la variabilidad de los perfiles), por filas el nivel que más contribuye es Repairs (0,312874) mientras que por columnas es Husband (0,381373). Este resultado no resulta sorprendente ya que ambos niveles son los más alejados del centro.

Con las coordenadas principales (las estándar reescaladas) de las dimensiones se puede construir un gráfico de las mismas utilizando la función plot(), pudiéndose optar por la proyección solo de las filas (usando los argumentos (map="colprincipal", what=c("none","all")), tal como se muestra en la Fig. 35.1:

par(mfrow = c(1, 2))
plot(ca_house, map = "rowprincipal", what = c("all", "none"), xlab = "Perfiles fila")
plot(ca_house, map = "colprincipal", what = c("none", "all"), xlab = "Perfiles columna")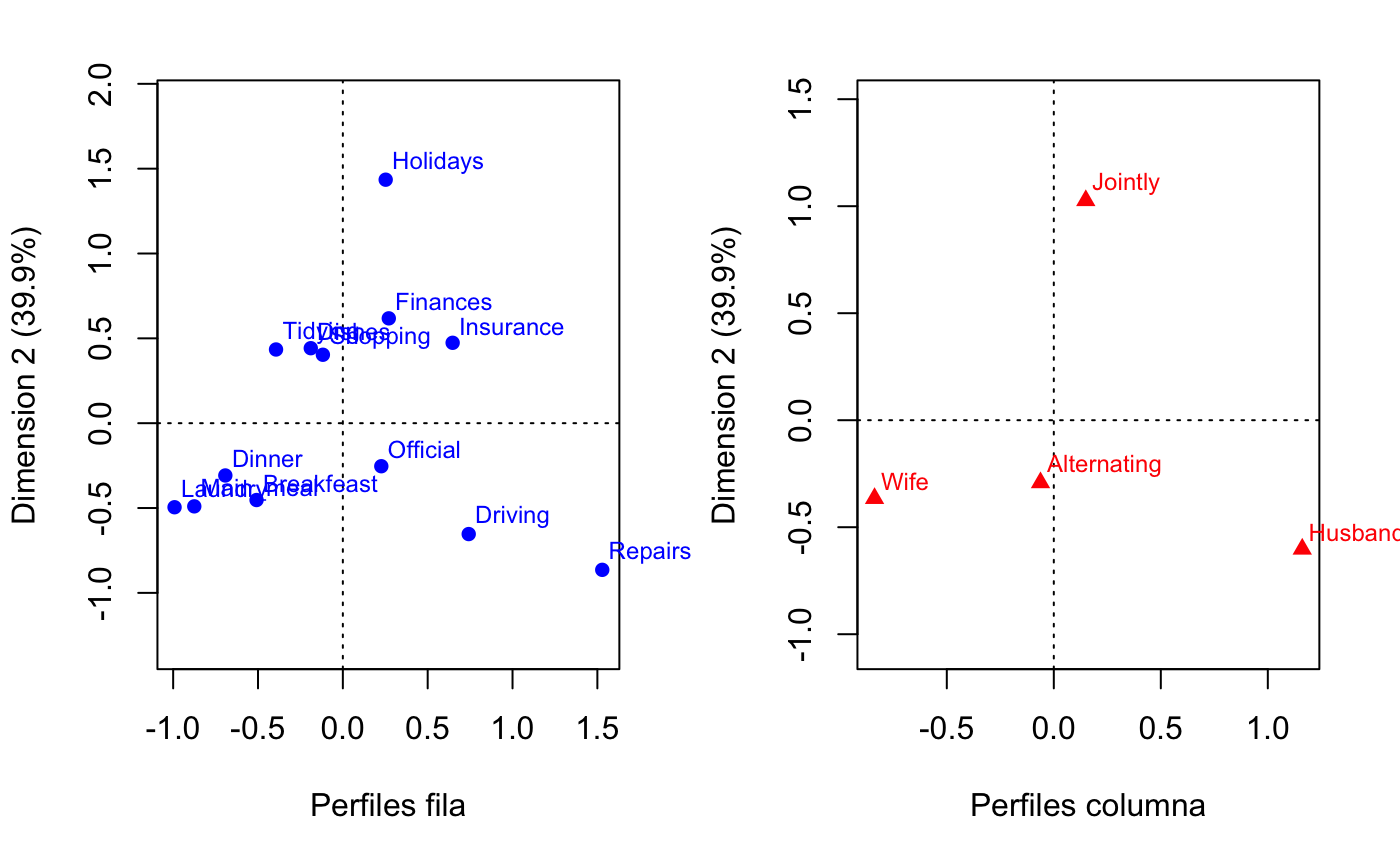

Figura 35.1: Proyecciones de los perfiles fila.

Respecto a las filas, se aprecian varios grupos: el compuesto por Breakfast, Dinner, Main_meal y Laundry; otro por Shopping, Dishes y Tidying; uno tercero por Insurance y Finance; y el compuesto por Driving y Official. Los niveles Holiday y Repairs están alejados del resto.

Las coordenadas simétricas permiten la representación de ambos factores a la vez (map= "symmetric", what=c("all","all")), como se muestra en la Fig. 35.2.

plot(ca_house,
  map = "symmetric", what = c("all", "all"),
  xlab = "Proyección común de ambos factores.", cex = 4.5
)

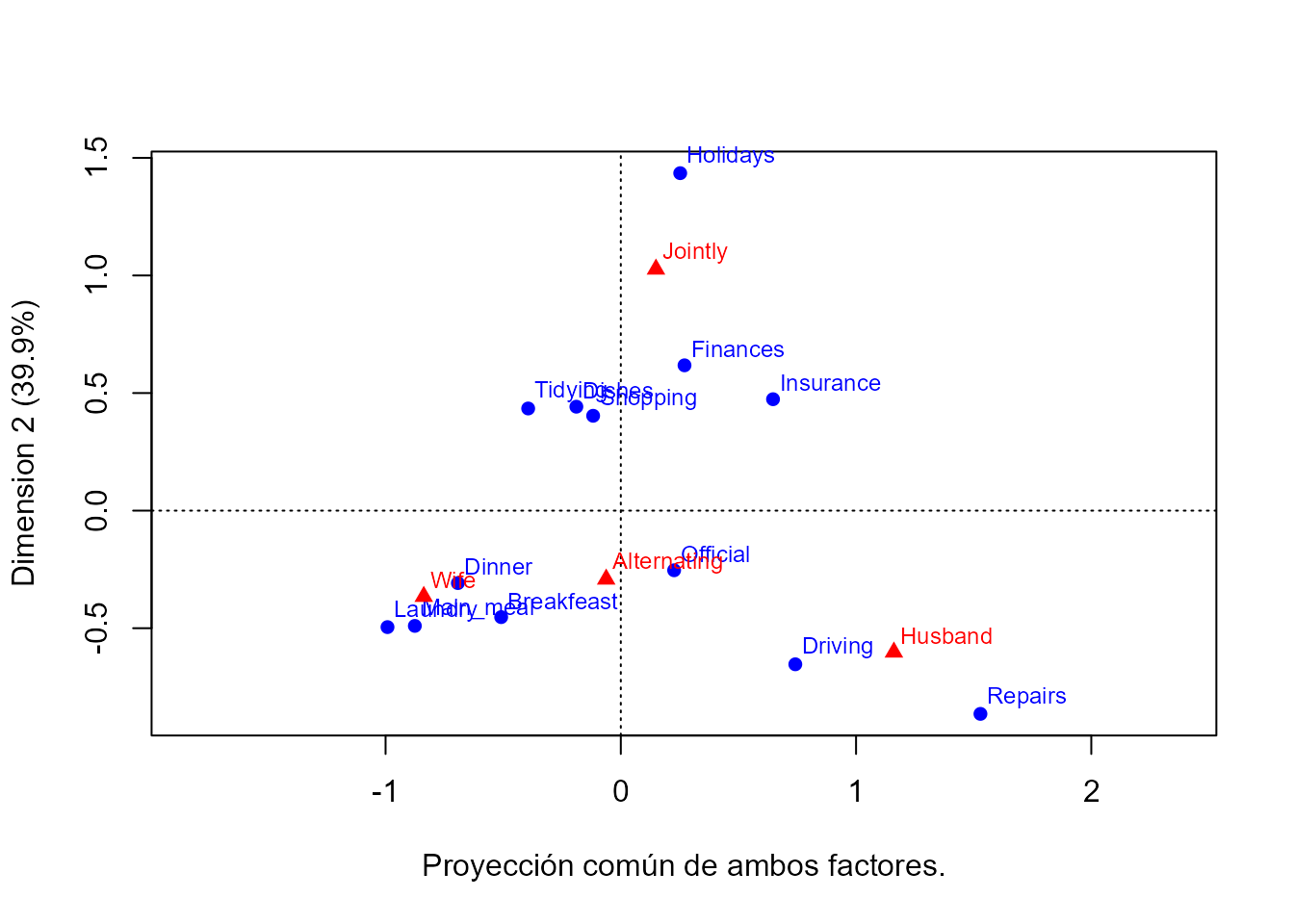
Figura 35.2: Proyección simétrica de ambos factores.

El gráfico conjunto permite observar qué niveles de filas y columnas pueden estar más cercanos (aproximación a la asociación entre ellos). El grupo de Driving y Repairs está cercano a Husband; el grupo de Dinner, Breakfast, Laundry y Main_meal está cercano a Wife; mientras que el nivel Jointly parece estar asociado a Holidays, Finance e Insurance.

35.3.2 Caso práctico 2: accidentes de tráfico en Madrid (2020)

Como segundo ejemplo, se utilizan los datos accidentes2020_data, contenidos en el paquete CDR; en concreto, la información sobre Tipo_accidente y Estado_meteorológico. Para evitar pares de niveles con frecuencia nula, se eliminan los niveles Atropello a animal, Despeñamiento y Otro del factor Tipo_accidente y los niveles Granizando, Nevando, NULL y Se desconoce del factor Estado_meteorológico.

library("CDR")
library("dplyr")
data("accidentes2020_data")
datos <- data.frame(
  V1 = as.factor(accidentes2020_data$tipo_accidente),
  V2 = as.factor(accidentes2020_data$estado_meteorológico)
)
levelsV1 <- c("Alcance", "Choque contra obstáculo fijo", "Colisión frontal", "Colisión fronto-lateral", "Colisión lateral", "Colisión múltiple")
levelsV2 <- c("Despejado", "Lluvia débil", "LLuvia intensa", "Nublado")
datos_depu <- droplevels(filter(datos, (V1 %in% levelsV1) & (V2 %in% levelsV2)))

table(datos_depu)
#>                               V2
#> V1                             Despejado Lluvia débil LLuvia intensa Nublado
#>   Alcance                           5525          403             84     449
#>   Choque contra obstáculo fijo      3258          308             43     224
#>   Colisión frontal                   711           42              5      48
#>   Colisión fronto-lateral           6359          398             51     494
#>   Colisión lateral                  3241          169             30     277
#>   Colisión múltiple                 1619          173             29     111

Se comprueba que existe asociación entre los factores en estudio y se obtienen los resultados del análisis de correspondencias:

tabla <- table(datos_depu)
chisq.test(tabla)
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  tabla
#> X-squared = 104, df = 15, p-value = 2e-15
ca_tabla <- ca(tabla, k = 2)
ca_tabla
#> 
#>  Principal inertias (eigenvalues):
#>            1        2        3      
#> Value      0.003804 0.000493 2.7e-05
#> Percentage 87.97%   11.4%    0.62%  
#> 
#> 
#>  Rows:
#>          Alcance Choque contra obstáculo fijo Colisión frontal
#> Mass     0.26864                       0.1594          0.03351
#> ChiDist  0.03200                       0.0817          0.06591
#> Inertia  0.00028                       0.0011          0.00015
#> Dim. 1  -0.16016                      -1.2818          0.72969
#> Dim. 2   1.36554                      -0.9207         -1.84795
#>         Colisión fronto-lateral Colisión lateral Colisión múltiple
#> Mass                     0.3036          0.15455            0.0803
#> ChiDist                  0.0446          0.07682            0.1284
#> Inertia                  0.0006          0.00091            0.0013
#> Dim. 1                   0.6586          1.22996           -2.0813
#> Dim. 2                  -0.8221          0.52856            0.1210
#> 
#> 
#>  Columns:
#>         Despejado Lluvia débil LLuvia intensa Nublado
#> Mass      0.86121       0.0621        0.01006 0.06665
#> ChiDist   0.01344       0.2145        0.28954 0.08391
#> Inertia   0.00016       0.0029        0.00084 0.00047
#> Dim. 1    0.20552      -3.4619       -3.67116 1.12291
#> Dim. 2   -0.19007      -0.8381        8.05783 2.02007

Las dos primeras dimensiones explican el 87,97 % y 11,4 % respectivamente, por lo que la representación en un plano engloba al 99,37 % de la inercia.

La representación gráfica de la proyección simétrica se muestra en la Fig. 35.3:

plot(ca_tabla,
  map = "symmetric", what = c("all", "all"),
  xlab = "Proyección común de ambos factores."
)

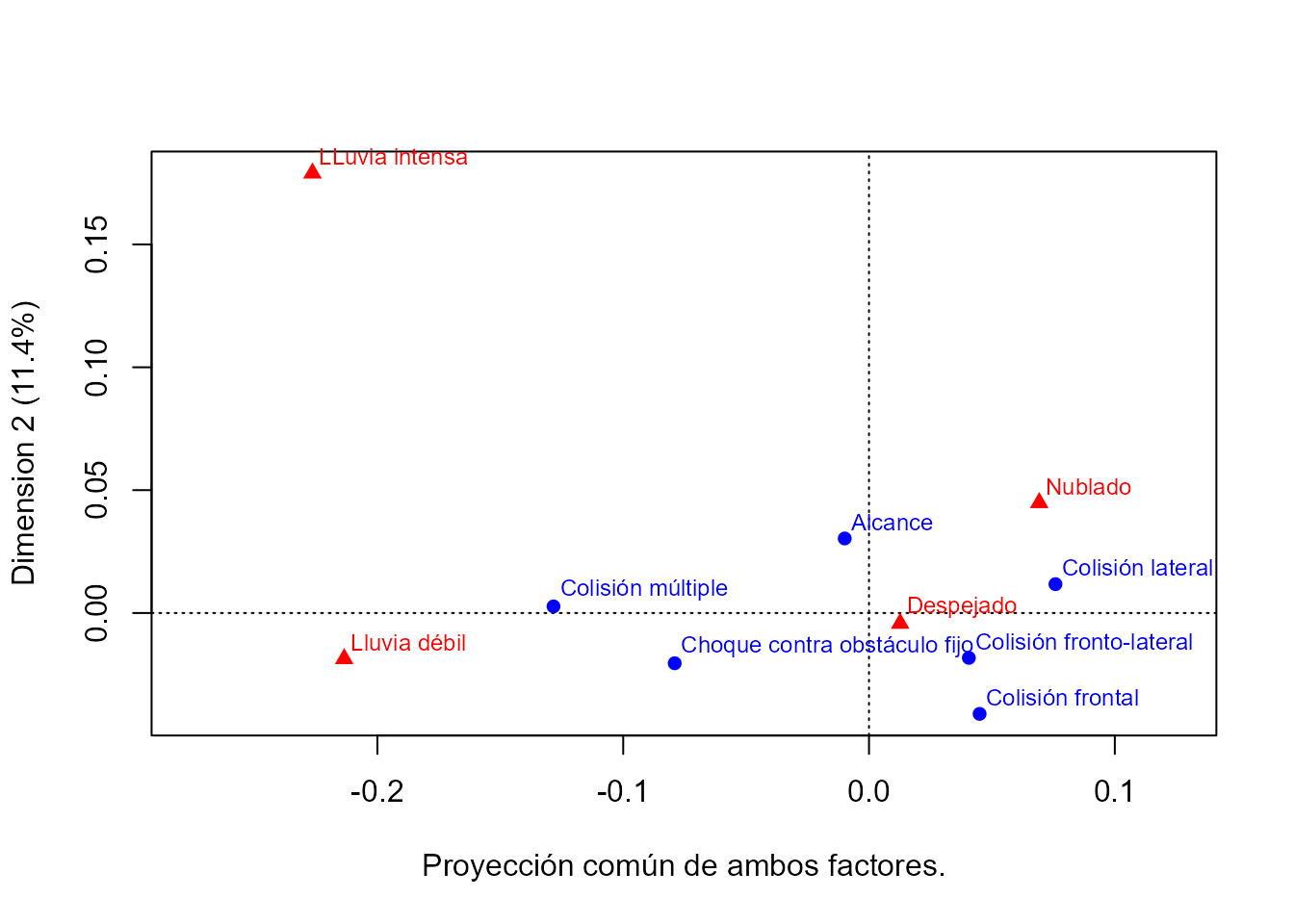
Figura 35.3: Proyección simétrica de ambos factores.

Se observa que Lluvia intensa no está especialmente asociada a ningún tipo de accidente. Sin embargo, Lluvia débil está asociada con Colisión múltiple y Choque contra obstáculo fijo; Despejado con Colisión fronto-lateral, Colisión frontal y Alcance; y Nublado con Colisión lateral.

Resumen

Dada una tabla de contingencia, el análisis de correspondencias reproduce:

Las distancias entre niveles de cada factor en un espacio de menor dimensión, permitiendo la comparación gráfica entre ellos.
La representación de los niveles de ambos factores en un espacio común.

En el primer caso, permite una visualización de la composición interna de cada factor, identificando los niveles que más se distancian del centroide. En el segundo, permite la representación de la asociación entre niveles de cada uno de los factores.

34 Escalamiento multidimensional

36 Redes neuronales artificiales