Capítulo 24 Árboles de clasificación y regresión
Ramón A. Carrasco\(^{a}\), Itzcóatl Bueno\(^{a,\hspace{0,05cm} b}\) y José-María Montero\(^{c}\)
\(^{a}\)Universidad Complutense de Madrid
\(^{b}\)Instituto Nacional de Estadística
\(^{c}\)Universidad de Castilla-La Mancha
24.1 Introducción
Los árboles de decisión son modelos o algoritmos no paraméticos que se utilizan principalmente para la resolución de problemas de clasificación, en los que hay que predecir las distintas categorías de la variable objetivo o dependiente, aunque también son aplicables a la predicción de valores numéricos de dicha variable objetivo, esto es, como modelos de regresión. De ahí que sean conocidos como árboles de clasificación y regresión (CART, classification and regression trees).
Específicamente, lo que hacen los árboles de decisión es utilizar una serie de reglas de decisión para dividir el espacio de características predictoras en un número menor de regiones disjuntas en cada una de las cuales los valores de la variable respuesta son similares.
Un árbol de decisión parte del conjunto de datos de entrenamiento, correspondiente a un nodo raíz, y lo va dividiendo recursivamente en subconjuntos de datos homogéneos, dando lugar a nuevos nodos. La manera de formar los subgrupos es mediante la formulación de preguntas con respuesta binaria (si la variable respuesta es “jugar al tenis” se formula la pregunta ¿Sí o No juega al tenis?; si es “pesa más o menos de 75 kg.” la pregunta es ¿el peso es \(\leq 75\) o \(>75\)?). El proceso de partición se lleva a cabo hasta que se alcanza algún criterio de parada previamente establecido. Es resultado que produce dicho proceso es el valor medio de la variable respuesta en las observaciones incluidas en cada subgrupo (en árboles de regresión) o la clase de la variable respuesta con presencia mayoritaria en ellos (cuando se trata de árboles de clasificación). En este último caso también proporciona, en cada subgrupo, una estimación de la probabilidad de pertenencia a cada clase.
Algunos ejemplos de árboles de decisión son:
- Clasificación: en la medida que la variable objetivo debe ser categórica, se podrían usar, por ejemplo, para tomar la decisión de qué empleados deberían promocionar (variable con dos categorías: sí promocionar o no promocionar) en base a sus méritos, capacidades, edad, etc. Otro ejemplo podría ser su uso para decidir si se juega o no un partido de tenis en base a la climatología prevista. Este ejemplo se muestra gráficamente en la Fig. 24.1. En este último caso, el algoritmo que se utilice indicará la decisión a tomar en base a los registros climatológicos de los partidos que ya se hayan jugado. Así, si un determinado día se quiere jugar al tenis, se deberán tomar como datos de entrada las previsiones de las variables (en este caso atributos) Tipo de día (soleado, nublado o lluvioso), Fuerza del Viento y Humedad. En caso de ser un día nublado, el algoritmo sugerirá que se juegue. En caso de ser soleado, comprobará el nivel de humedad y, si no es muy elevada, recomendará que se juegue el partido. Lo mismo pasará si la previsión es de lluvia pero la fuerza del viento prevista no es lo suficientemente elevada como para impedir el normal desarrollo del partido.
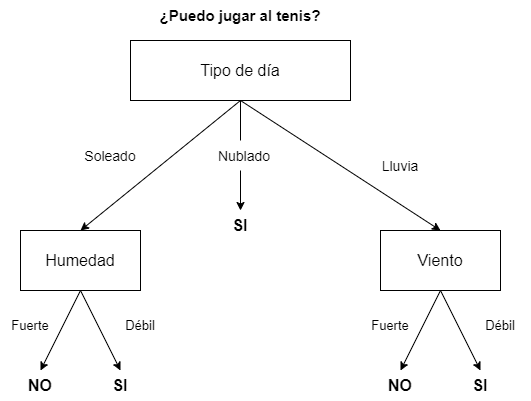
Figura 24.1: Ejemplo de árbol de decisión.
- Regresión: siguiendo con el ejemplo del partido de tenis, también se puede utilizar un árbol de decisión para determinar cuántas horas jugar de acuerdo a las condiciones climatológicas. En la Fig. 24.1 se sustituirían la predicciones dicotómicas SÍ/NO por valores numéricos, como se muestra en la Fig. 24.2. Por ejemplo, el algoritmo puede sugerir jugar 5 horas si el día está soleado pero la humedad es del 30% de vapor de agua por \(\text{m}^3\); y 3,5 horas si está soleado pero la humedad es del 80%. También puede decidir que si el día está nublado se jueguen 4 horas. O en caso de lluvia, podría decidir que el partido dure 0,75 horas si la fuerza del viento es de 62 km/h y 1,15 horas si es de 27 km/h.
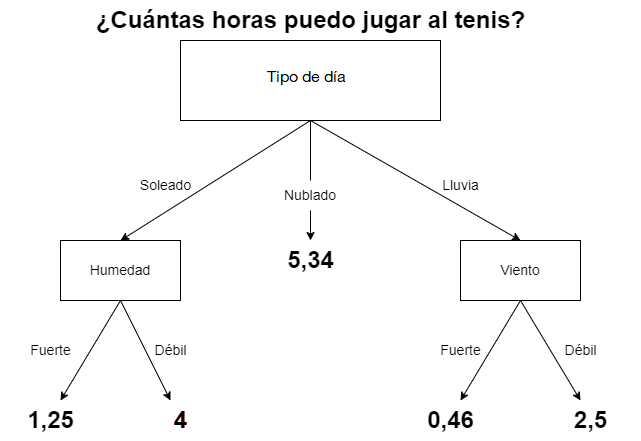
Figura 24.2: Ejemplo de árbol de regresión.
Como se ha comentado anteriormente, CART es un término genérico para describir este tipo de algoritmos de árbol y también un nombre específico para el algoritmo original de Breiman et al. (1984) de construcción de árboles de clasificación y regresión. Sin embargo, existen otros como el ID3 (induction decision trees), o el C4.5, que está basado en el ID3. En la Tabla 24.1 se muestra una pequeña comparativa de estos tres algoritmos:
| Algoritmo | Criterio de división | Tipo de variables input | Estrategia de poda |
|---|---|---|---|
| ID3 | Ganancia de información | Solo categóricas | No poda |
| CART | Índice de Gini | Categóricas y numéricas | Poda basada en el coste de complejidad |
| C4.5 | Ratio de ganancia | Categóricas y numéricas | Poda basada en el error |
Los árboles de decisión tienen múltiples ventajas. Entre ellas destacan:
- Son fáciles de entender e interpretar. Su visualización es muy clara y permite interpretar fácilmente la salida del modelo, así como entender su proceso como un conjunto de condicionantes.
- El mismo algoritmo incorporado en R (
CART) es válido tanto para problemas de clasificación como de regresión y, por tanto, la variable objetivo puede ser continua o categórica. Respecto a las variables de entrada, las independientes pueden ser tanto categóricas como numéricas. Al contrario de lo que ocurre con otros algoritmos, este último tipo de variables no necesitan ser estandarizadas, puesto que los árboles de decisión se basan en reglas y no en el cálculo de distancias entre observaciones. - Tratan mejor que otros algoritmos el problema de la no linealidad.
- Respecto a los datos, llevan a cabo un tratamiento automático de valores ausentes (en la mayoría de los árboles de clasificación) y no se ven afectados por las observaciones atípicas.
Sin embargo, también tienen ciertas desventajas:
- Son inestables, ya que la inclusión de una nueva observación en la fase de entrenamiento obliga a reconstruirlo, pudiendo modificar la estructura del árbol final.
- No son recomendables en caso de grandes conjuntos de datos, puesto que el modelo entrenado puede estar sobreajustado. Este sobreajuste es el principal problema de los árboles de decisión, ya que modelos demasiados complejos pueden ajustar muy bien los datos observados, pero también pueden cometer muchos errores en la fase de predicción. Cuando se da esta circunstancia, el modelo ha aprendido los datos de entrenamiento pero no la generalidad del problema, que es lo que normalmente se pretende. El sobreajuste da lugar también a una varianza elevada.
- Tienen una capacidad predictiva inferior a la de otros algoritmos más complejos, como las redes neuronales artificiales y los splines de regresión adaptativos multivariantes (MARS), aunque es cierto que si se combina adecuadamente un número elevado de árboles de decisión, mediante las técnicas de bagging y boosting (véanse Caps. 28 y 29, respectivamente), la potencia predictiva mejora sustancialmente.
24.2 Procedimiento con R: la función rpart()
En el paquete rpart de R se encuentra la función rpart() que se
utiliza para entrenar un árbol de decisión:
rpart(formula, data, ...)-
formula: refleja la relación entre la variable dependiente \(Y\) y los predictores tal que \(Y \sim X_1 + ... + X_p\). -
data: conjunto de datos con el que entrenar el árbol de acuerdo a la fórmula indicada.
24.3 Árboles de clasificación
Como se avanzó en la sección anterior, formalmente, un árbol de decisión es un grafo acíclico (un grafo sin ciclos, siendo un ciclo un circuito completo) que se inicia en un nodo raíz, el cual se divide en ramas, también conocidas como aristas. De las ramas salen las hojas, también denominadas nodos. Estos nodos pueden ser nodos finales, o puntos de decisión, (si de ellos no salen nuevas ramas con nuevos nodos) o no ( si de ellos salen nuevas ramas con nuevas hojas o nodos) y así hasta que todos los nodos sean puntos de decisión. En el ejemplo de la Fig. 24.1 el nodo raíz es la caja Tipo de día. Las ramas o aristas son sus tres niveles o categorías: Soleado, Nublado o Lluvia. Cada una de estas ramas conecta con una nueva hoja o nodo: Humedad o Viento en los casos de soleado o lluvia, respectivamente. Sin embargo, en ese ejemplo, Nublado representa un nodo terminal, puesto que, llegados a ese punto, la salida que proporcionaría el árbol es Jugar al tenis. Este proceso se repite utilizando el conjunto de datos disponible en cada hoja, generándose una clasificación final cuando una hoja no tenga ramas nuevas, en cuyo caso recibe la denominación de nodo final. El objetivo es que el árbol sea lo más general y pequeño posible. Esto se consigue seleccionando, en cada paso, la variable que optimice la división de los datos en subconjuntos homogéneos, de tal forma que se prediga mejor la clase objetivo.
La Fig. 24.3 ilustra la nomenclatura relativa a los elementos del árbol mencionados anteriormente.
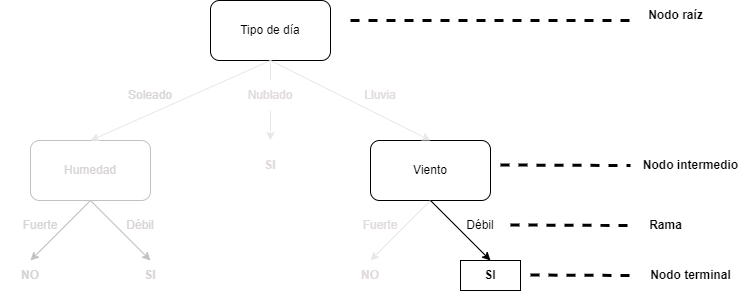
Figura 24.3: Ejemplo de formación de árbol de decisión.
24.3.1 ¿Cómo se va formando el árbol de clasificación?
Como ya se ha mencionado, la construcción de un árbol de decisión se basa en la división recursiva en nuevas ramas, es decir, cada división está condicionada por las anteriores. El objetivo en cada nodo es encontrar la variable (o atributo, como en este caso) más adecuada para dividir los datos de ese nodo en dos nuevos subconjuntos, de tal forma que el error global entre la clase observada y la predicha por el árbol se minimice. Para la construcción de árboles de clasificación, el algoritmo CART utiliza la medida de impureza de Gini para generar las particiones, mientras que los algoritmos ID3 y C4.5 están basados en medidas de entropía.
24.3.1.1 Impureza de Gini
La impureza de Gini es una medida de la frecuencia con la que una observación elegida aleatoriamente de un conjunto de observaciones (en este caso los conjuntos de observaciones correspondientes a los nodos) se asignaría a la clase errónea si se etiqueta al azar en una de las clases que se consideran. Formalmente, sea \(\bf{X}\) un conjunto de datos con \(\kappa\) clases, y sea \(p_i\) la probabilidad de que una observación pertenezca a la clase \(i=1,...,\kappa\). La impureza de Gini para \(\bf{X}\) se define como:
\[\begin{equation} Gini({\bf{X}}) = 1 - \sum^{\kappa}_{i=1}{p^{2}_{i}}, \end{equation}\]donde, en este caso, al ser la respuesta binaria, \({\bf{\kappa}}=2\).
A la hora de construir el árbol se selecciona el atributo con menor impureza ponderada de Gini para dividir en dos el conjunto de datos \(\bf{X}\) correspondiente al nodo del que se trate: el subconjunto con el primer valor de la variable respuesta, \({\bf{X}}_1\) y el subconjunto con el segundo valor de la variable respuesta, \({\bf{X}}_2\).
Si en un nodo el subconjunto de datos se divide en dos subconjuntos \(\bf{\bf {X}}_1\) y \({\bf{X}}_2\), con tamaños \(n_1\) y \(n_2\), respectivamente, la impureza ponderada de Gini se define como:
\[\begin{equation} Gini_{\varphi}({\bf{X}}) = \frac{n_1}{n}{Gini \left(\bf{X}_{1}\right) } + \frac{n_2}{n}{Gini \left({\bf{X}}_{2}\right)}, \end{equation}\]donde las probabilidades se computan a partir de las correspondientes frecuencias relativas.
En el ejemplo de la Fig. 24.1 considérese la situación reflejada en la Tabla 24.2:
| Día | Tipo de día | Humedad | Viento | Decisión |
|---|---|---|---|---|
| 1 | Soleado | Fuerte | Débil | NO |
| 2 | Soleado | Fuerte | Fuerte | NO |
| 3 | Lluvia | Fuerte | Débil | SÍ |
| 4 | Nublado | Fuerte | Débil | SÍ |
| 5 | Lluvia | Débil | Débil | SÍ |
| 6 | Lluvia | Débil | Fuerte | NO |
| 7 | Soleado | Fuerte | Débil | NO |
| 8 | Nublado | Débil | Fuerte | SÍ |
| 9 | Soleado | Débil | Débil | SÍ |
| 10 | Lluvia | Débil | Débil | SÍ |
| 11 | Soleado | Débil | Fuerte | SÍ |
| 12 | Nublado | Fuerte | Fuerte | SÍ |
| 13 | Nublado | Débil | Débil | SÍ |
| 14 | Lluvia | Fuerte | Fuerte | SÍ |
| 15 | Soleado | Fuerte | Fuerte | NO |
Lo primero que se ha de decidir es cuál es el nodo raíz del árbol (el punto de partida del proceso recursivo de partición). Hay tres candidaturas: la de Tipo de día, la de Humedad y la de Fuerza del viento. Se elegirá aquella con menor impureza ponderada de Gini.
Comenzando, por ejemplo, con el Tipo de día, el conjunto de datos se divide en tres subconjuntos (de 6, 4 y 5 observaciones, respectivamente), tal y como muestra la Tabla 24.3:
| Tipo de día | SÍ | NO | # observaciones |
|---|---|---|---|
| Soleado | 2 | 4 | 6 |
| Nublado | 4 | 0 | 4 |
| Lluvia | 4 | 1 | 5 |
La impureza de Gini para cada una de las tres categorías es: \[\begin{equation*} Gini(Soleado) = 1 - \Bigl(\frac{2}{6}\Bigr)^{2} - \Bigl(\frac{4}{6}\Bigr)^{2} = \text {0,45}, \end{equation*}\] \[\begin{equation*} Gini(Nublado) = 1 - \Bigl(\frac{4}{4}\Bigr)^{2} = 0, \end{equation*}\] \[\begin{equation*} Gini(Lluvia) = 1 - \Bigl(\frac{4}{5}\Bigr)^{2} - \Bigl(\frac{1}{5}\Bigr)^{2} = \text {0,32}. \end{equation*}\]
siendo la pregunta que se formula: ¿Se juega al tenis?, con respuestas SÍ y NO.
La suma ponderada de las anteriores impurezas proporciona la impureza ponderada (de Gini) de variable Tipo de día:
\[\begin{equation*} Gini(Tipo \hspace{0,1cm}de \hspace{0,1cm} día) = \text {0,45}\cdot\Bigl(\frac{6}{15}\Bigr) + 0\cdot\Bigl(\frac{4}{15}\Bigr) + \text {0,32}\cdot\Bigl(\frac{5}{15}\Bigr) = \text {0,29}. \end{equation*}\]Del mismo modo, se puede calcular la impureza ponderada de Gini de Humedad y Viento, los dos nodos candidatos a ser nodo raíz. La Tabla 24.4 y la Tabla 24.5 presentan los subconjuntos de datos que se forman para cada una de sus categorías, respectivamente. A partir de dichas impurezas, debajo de cada tabla, se calcula la impureza ponderada de cada uno de estos dos nodos candidatos.
| Humedad | SÍ | NO | # observaciones | \(p_{SÍ}\) | \(p_{NO}\) | Impureza de Gini |
|---|---|---|---|---|---|---|
| Fuerte | 4 | 4 | 8 | 0,50 | 0,50 | 0,50 |
| Débil | 6 | 1 | 7 | 0,86 | 0,14 | 0,76 |
| Viento | SÍ | NO | # observaciones | \(p_{SÍ}\) | \(p_{NO}\) | Impureza de Gini |
|---|---|---|---|---|---|---|
| Fuerte | 4 | 3 | 7 | 0,57 | 0,43 | 0,49 |
| Débil | 6 | 2 | 8 | 0,75 | 0,25 | 0,38 |
En la Tabla 24.6 se muestran las impurezas ponderadas de cada una de las variables candidatas a ser nodo raíz. Se puede comprobar que la menor impureza ponderada de Gini corresponde a Tipo de día; por consiguiente, se elige como nodo raíz del árbol de clasificación.
| Variable | Impureza ponderada de Gini |
|---|---|
| Tipo de día | 0,29 |
| Humedad | 0,62 |
| Viento | 0,43 |
La siguiente decisión a tomar es: en cada categoría de Tipo de día, ¿qué variable (Humedad o Viento) se elige para llevar a cabo una nueva partición del subconjunto de datos correspondiente cada una de ellas? La respuesta a esta pregunta la proporciona la ganancia de información, \(\Delta Gini()\), correspondiente a cada una de estas dos variables:
\[\begin{equation} \Delta Gini(\varphi) = Gini({\bf{X}}) - Gini_{\varphi}({\bf{X}}), \end{equation}\]si bien, como puede comprobarse, la mayor ganancia de información corresponde a la menor impureza ponderada de Gini, puesto que \(Gini({\bf{X}})\) permanece constante.
Por ejemplo, para obtener la ganancia de información para Humedad en cada una de las categorías de Tipo de día,185 la impureza ponderada de Humedad se resta de la impureza de cada una de las tres categorías de Tipo de día. Lo mismo se haría con Viento.
Dicho lo anterior, para la categoría Tipo de día: soleado, la Tabla 24.7 muestra el valor de las impurezas ponderadas de las dos variables candidatas a ser las nuevas “particionadoras”:
| Variable | Impureza ponderada de Gini |
|---|---|
| Humedad | 0,00 |
| Viento | 0,44 |
Entonces, la ganancia de Gini para cada variable es:
Puede observarse que, en la categoría Tipo de día: soleado, la ganancia de información que se obtiene al particionar el subconjunto de datos correspondiente a dicha categoría según Humedad es mayor (en realidad mucho mayor) que al hacerlo según Viento, por lo que Humedad es la variable elegida para realizar la partición del subconjunto de datos de la categoría Tipo de día: soleado, como se observa en la Fig. 24.1.
En el caso de la categoría Tipo de día: nublado, el subconjunto de observaciones es de tamaño 4 y en todas ellas la categoría de la variable respuesta es SÍ (se juega al tenis); su impureza es nula. Por tanto, no tiene sentido realizar partición alguna del subconjunto de datos, ni según Humedad ni según Viento. Se trata de un punto de decisión final.
Finalmente, para la categoría Tipo de día: con lluvia, con un subconjunto de 5 observaciones y una impureza de Gini de 0,32, la impureza ponderada correspondiente a Humedad es de 0,267, mientras que la correspondiente a Viento es 0,20, por lo que la ganancia de información de tomar como variable divisora Humedad es 0,053 mientras que se eleva a 0,12 cuando la variable divisora es Viento (se deja al lector la labor de comprobar etos cálculos). Es por eso que, como puede verse en Fig. 24.1, se elige esta última para realizar una nueva partición en el subconjunto de datos Tipo de día: con lluvia.
En este punto del proceso de partición (o crecimiento del árbol) ya se tiene primer nivel de nodos, que surgen del nodo raíz. A partir de este primer nivel, siguiendo el mismo proceso llevado a cabo más arriba, se obtendría un segundo nivel de nodos, y a partir de estos, un tercero, y así sucesivamente hasta que el criterio de parada preestablecido indique que el proceso de finalización ha terminado. En el ejemplo propuesto, al ser tan sencillo, pues el conjunto de datos solo cuenta con tres variables predictoras, solo se va a decidir cuál es el nodo raíz y cuáles los que componen el primer nivel de nodos. Con tres variables predictoras no se pueden obtener más niveles de nodos.
24.3.1.2 Entropía
La entropía es un concepto matemático que mide el grado de incertidumbre que se tiene en relación con un conjunto de datos, es decir, la varianza en los datos entre diferentes clases. Dada una variable predictora, para los conjuntos de datos de cada una de sus categorías, la entropía se calcula como:
\[\begin{equation} E = -p_1\log_2 (p_1) - p_2\log_2 (p_2), \tag{24.1} \end{equation}\]donde \(p_1\) y \(p_2\) representan la probabilidad de pertenecer a cada una de las clases de la variable respuesta (en este caso dos) en ese nodo, y se estiman mediante sus correspondientes frecuencias relativas. En teoría de la información, la base logarítmica varía dependiendo de la aplicación, y con ella varía la unidad de medida.
Se denomina entropía ponderada de la variable a la suma ponderada de las entropías correspondientes a sus categorías, siendo las ponderaciones el número de observaciones en cada categoría dividido por el número de observaciones correspondientes a la variable en el nodo del que se trate.
Finalmente, se define ganancia de información, \(IG\), como:
\[\begin{equation} IG = E_{\varkappa} - E_{\varkappa + 1}, \end{equation}\]donde \(E_\varkappa\) representa la entropía en el nodo “padre” (en el conjunto de datos que se está particionando), mientras que \(E_{\varkappa+1}\) representa la entropía en cada categoría de dicho nodo padre (en el conjunto de datos de cada categoría de la variable del nodo padre).
Lógicamente, se elige como variable “particionadora” aquella en la que que se obtiene mayor ganancia de información con la partición.
Volviendo de nuevo al ejemplo basado en los datos de la Tabla 24.3, para generar el árbol de clasificación se siguen los mismos pasos que en la subsección anterior, pero sustituyendo la medida de impureza por la medida de entropía.
Se parte de la entropía existente en el conjunto total de datos:
\[\begin{equation*} E = -\frac{10}{15}\log_2 \Bigl(\frac{10}{15}\Bigr) - \frac{5}{15}\log_2 \Bigl(\frac{5}{15}\Bigr) = \text {0,9183}. \end{equation*}\]y, en cada nodo, se va dividiendo el árbol en función de la variable que más reduzca la entropía existente en dicho nodo.
La primera decisión es la relativa a cuál de las tres variables predictoras ocupará el nodo raíz. Para ello, se procede como sigue:186
- Para cada una de las variables predictoras se calcula la entropía de cada una de sus categorías o niveles.
- A partir de dichas entropías, ponderándolas adecuadamente, se calcula la entropía de cada una de las variables predictoras.
- Se calcula la ganancia de información que se obtiene al dividir el conjunto de datos según dicha variable restando de la entropía del conjunto de datos total la entropía ponderada de cada variable.
- El conjunto de datos se divide en función de la variable con la que se tenga más ganancia de información.
Comenzando por la variable Tipo de día se calcula:
\[\begin{equation*} E_{Soleado} = -\frac{2}{6}\log_2 \Bigl(\frac{2}{6}\Bigr) - \frac{4}{6}\log_2 \Bigl(\frac{4}{6}\Bigr) = \text{0,9183}, \end{equation*}\] \[\begin{equation*} E_{Nublado} = -\frac{4}{4}\log_2 \Bigl(\frac{4}{4}\Bigr) - \frac{0}{4}\log_2 \Bigl(\frac{0}{4}\Bigr) = 0, \end{equation*}\] \[\begin{equation*} E_{Lluvia} = -\frac{4}{5}\log_2 \Bigl(\frac{4}{5}\Bigr) - \frac{1}{5}\log_2 \Bigl(\frac{1}{5}\Bigr) = \text {0,7219}. \end{equation*}\]
Con lo que se tiene que:
\[\begin{equation*} E_{\text{Tipo de día}} = \frac{6}{15}\cdot \text {0,9183} + \frac{4}{15}\cdot 0 + \frac{5}{15}\cdot \text {0,7219} = \text {0,608}, \end{equation*}\]y que:
\[\begin{equation*} IG_{\text{Tipo de día}} = E - E_{\text{Tipo de día}} = \text {0,918} - \text {0,608} = \text {0,310}. \end{equation*}\]
Repitiendo el mismo procedimiento con las variables Viento y Humedad se puede comprobar que \(E(Viento) = \text {0,893}\) y \(E(Humedad) = \text{0,809}\), con lo que:
\[\begin{equation*} IG_{Viento} = E - E_{Viento} = \text {0,918 - 0,893 = 0,025}, \end{equation*}\] \[\begin{equation*} IG_{Humedad} = E - E_{Humedad} = \text {0,918 - 0,809 = 0,109}, \end{equation*}\]
pudiéndose comprobar que la disminución de la aleatoriedad, o la ganancia de información, es mayor para la variable Tipo de día y, por tanto, se elige para ser el nodo raíz. Repitiendo este proceso, igual que se hizo en la subsección anterior, se va construyendo el árbol hasta alcanzar los nodos terminales.
24.3.2 Sobreajuste
Ya se ha comentado en la Sec. 24.1 que una de las principales desventajas de los árboles de decisión es su propensión a sobreajustar el modelo al conjunto de datos de entrenamiento y, por tanto, hay que prestar especial atención a la complejidad del modelo. Basándose en las observaciones utilizadas en la fase de entrenamiento, un árbol de decisión puede extraer los patrones presentes en el conjunto de observaciones de entrenamiento y ser muy preciso en el ajuste de dichas observaciones. Sin embargo, puede ocurrir que el árbol resultante no sea capaz de clasificar correctamente ni el conjunto de validación aun con nuevas observaciones. Esta circunstancia puede ocurrir porque haya patrones no observados en los datos de entrenamiento que el modelo no es capaz de detectar, o porque la división de los datos entre entrenamiento y validación no se realizó correctamente siendo los datos de entrenamiento no representativos del conjunto de datos completo. Al intentar que el árbol entrenado tenga la capacidad de aprender patrones muy complejos, se puede producir este sobreajuste, que se materializa en árboles muy profundos. La forma de evitar el sobreajuste es controlar el crecimiento del árbol para evitar que se vuelva excesivamente complejo.
24.3.3 ¿Cuánto debe crecer un árbol de clasificación?
En cada paso de construcción del árbol se determina la variable óptima para realizar la división de las observaciones de un nodo padre en sus nodos hijos. La pregunta es: ¿cuándo se detiene?, ¿cuál es el criterio de parada? Por ejemplo, se puede utilizar como criterio de parada que el árbol alcance un tamaño o profundidad determinado, para que no sea excesivamente complejo y así no tengan lugar las consecuencias derivadas del sobreajuste.
Por consiguiente, se debe llegar a un equilibrio entre la profundidad y complejidad del árbol para optimizar la predicción de observaciones futuras. Este equilibrio se puede lograr siguiendo alguno de los siguientes enfoques: la parada temprana o la poda.
24.3.3.1 La parada temprana
La parada temprana restringe el crecimiento del árbol, tanto de clasificación como de regresión, de forma explícita. Existen distintas maneras de imponer al árbol esta restricción, pero dos de las técnicas más populares son: \((i)\) restringir la profundidad a un cierto nivel y \((ii)\) establecer un número mínimo de observaciones permitidas en un nodo terminal. En el primer caso, el árbol deja de dividirse al llegar a cierta profundidad. Así, cuanto menos profundo sea el árbol, menos variación habrá en las predicciones que proporcione. Sin embargo, existe el riesgo de introducir mucho sesgo al modelo al no ser capaz de captar interacciones y patrones complejos en los datos. El segundo enfoque lo que provoca es que no se dividan nodos intermedios con pocas observaciones. Llevando el razonamiento al extremo, si se permite que un nodo terminal tenga solo una observación, esta actuaría como predicción, si bien su variabilidad sería muy elevada. Si, por el contrario, se exige un gran número de observaciones en los nodos terminales, se reduce el número de divisiones y, por lo tanto, se reduce la varianza, pero puede haber patrones interesantes en los datos que el árbol no es capaz de detectar y aprender.
24.3.3.2 La poda
El otro enfoque es el de la poda, que consiste en construir un árbol muy profundo y complejo y después podarlo para encontrar el subárbol óptimo. En este proceso, se utiliza un hiperparámetro de complejidad \((\zeta)\) que penaliza la función objetivo de la partición por el número de nodos terminales del árbol \((\tau)\). El subárbol óptimo es aquel que minimiza:
\[\begin{equation} R_{\zeta}(\tau) = R(\tau) + \zeta|\tau|, \tag{24.2} \end{equation}\]donde \(R(\tau)\) es la tasa total de clasificación errónea en los nodos terminales, \(|\tau|\) es el número total de nodos y \(\zeta\) es el hiperparámetro de complejidad. A medida que \(\zeta\) aumenta, más ramas del árbol son podadas, mientras que para valores más bajos los modelos resultantes son más complejos y, en consecuencia, más grandes. En conclusión, a medida que el árbol crece, el error de entrenamiento (la tasa total de clasificación errónea en los nodos terminales) debe tener una reducción mayor que el término de penalización por complejidad.
24.3.4 Ejemplo: árbol de clasificación para determinar la intención de compra
A continuación se describe el caso que se va a resolver mediante modelos de clasificación tanto en este como en los siguientes capítulos.
Existen diversas aserciones para definir Comercio Electrónico (CE). Entre ellas, la Organización para la Cooperación y el Desarrollo Económico (OCDE) lo define como el proceso de compra, venta o intercambio de bienes, servicios e información a través de redes de comunicación, comúnmente Internet. La clasificación más básica del CE se hace en base al tipo de entes que se relacionan: empresas (businesses, B), consumidores (consumers, C) y entes públicos (governments, G). De esta forma, una empresa de CE convencional suele ser B2B si vende a otras empresas, B2G si su relación comercial es con administraciones o B2C si vende a consumidores finales.
En este caso, se puede considerar que la empresa Beauty eSheep lleva a cabo un CE de tipo B2C. Su producto estrella es una crema hidratante unisex, denominada internamente como “Crema Luxury”, con mucho éxito entre su clientela. A partir de este producto inicial, la empresa ha ido ofreciendo un catálogo de productos tanto de belleza como de bienestar y salud.
Hace tiempo la empresa instauró una estrategia relacional, centrada en los clientes, de tal manera que han ido recabando diversos datos sobre ellos, incluidas las distintas compras que han realizado.
Basándose en los datos recopilados para cada cliente, la empresa quiere realizar una campaña para impulsar la venta de tensiómetros digitales. La empresa tiene acceso a un stock de estos productos, muy flexible en cuanto a fechas de envío, y el precio de los tensiómetros es muy bueno, por lo que se espera una buena rentabilidad en su venta.
Por tanto, en este proyecto hay que identificar el público objetivo susceptible de comprar dicho producto para ofrecérselo a través de la plataforma de CE de la compañía, SMS y/o webmail durante el periodo que dura la campaña.
La tabla con los datos integrados a nivel de cliente, incluyendo el
consumo de los distintos productos de la empresa, es dp_ENTR,
incluida en el paquete CDR, y se resume en la Tabla
24.8. Este ejemplo se va a replicar en el resto de
capítulos de machine learning supervisado para clasificación.
| VARIABLE | TIPO187 | DESCRIPCIÓN |
|---|---|---|
CLS_PRO_pro13 |
Factor | Clase objetivo, es un indicador de si el cliente es consumidor de ese producto “tensiómetro digital”. Sí (‘S’) o no (‘N’) |
ind_pro11 |
Factor | Indicador de si el cliente es consumidor del producto “fragancia luxury”. Sí (‘S’) o no (‘N’) |
ind_pro12 |
Factor | Indicador de si el cliente es consumidor del producto “depiladora eléctrica”. Sí (‘S’) o no (‘N’) |
ind_pro14 |
Factor | Indicador de si el cliente es consumidor del producto “crema luxury”. Sí (‘S’) o no (‘N’) |
ind_pro15 |
Factor | Indicador de si el cliente es consumidor del producto “smartwatch fitness”. Sí (‘S’) o no (‘N’) |
ind_pro16 |
Factor | Indicador de si el cliente es consumidor del producto “kit pesas inteligentes”. Sí (‘S’) o no (‘N’) |
ind_pro17 |
Factor | Indicador de si el cliente es consumidor del producto “estimulador muscular”. Sí (‘S’) o no (‘N’) |
importe_pro11 |
Doble | Importe neto global gastado por el cliente en ese producto, en euros |
importe_pro12 |
Doble | Importe neto global gastado por el cliente en ese producto, en euros |
importe_pro14 |
Doble | Importe neto global gastado por el cliente en ese producto, en euros |
importe_pro15 |
Doble | Importe neto global gastado por el cliente en ese producto, en euros |
importe_pro16 |
Doble | Importe neto global gastado por el cliente en ese producto, en euros |
importe_pro17 |
Doble | Importe neto global gastado por el cliente en ese producto, en euros |
edad |
Entero | Edad del cliente |
tamano_fam |
Entero | Número de miembros de la unidad familiar a la que pertenece el cliente, él incluido |
anos_exp |
Entero | Años de trabajo del cliente |
ingresos_ano |
Doble | Ingresos anuales del cliente, en euros |
des_nivel_edu |
Factor | Descripción del nivel de educación del cliente |
A partir del conjunto de entrenamiento, se construye un árbol de clasificación, tal y como se ha expuesto anteriormente, sin
transformar (en su escala original) mediante el algoritmo CART
implementado en el paquete rpart con árboles de regresión y partición
recursiva (recursive partitioning and regression trees, RPART), que se
puede usar tanto para regresión como para clasificación.
library("CDR")
library("reshape")
library("caret")
library("rpart")
library("rpart.plot")
library("ggplot2")
data("dp_entr")
head(dp_entr)
ind_pro11 ind_pro12 ind_pro14 ind_pro15 ind_pro16 ind_pro17 importe_pro11
1 S N S S S N 157
497 N N S N S N 0
265 N N S S S S 0
534 N S S N N N 0
415 N S S N S N 0
298 S N S N N N 115
importe_pro12 importe_pro14 importe_pro15 importe_pro16 importe_pro17 edad
1 0 40 200 180 0 49
497 0 240 0 180 0 38
265 0 425 200 180 300 61
534 120 60 0 0 0 47
415 120 133 0 180 0 34
298 0 220 0 0 0 43
tamano_fam anos_exp ingresos_ano des_nivel_edu CLS_PRO_pro13
1 4 24 30000 MEDIO S
497 2 12 53000 MEDIO N
265 4 37 172000 BASICO S
534 3 21 38000 MEDIO N
415 1 10 38000 BASICO N
298 2 18 60000 ALTO N
trControl <- trainControl(
method = "cv",
number = 10,
classProbs = TRUE,
summaryFunction = twoClassSummary
)En primer lugar, se carga la librería necesaria para entrenar el modelo, así como los datos de compras de los clientes. En este caso se usa el método de remuestreo de validación cruzada con 10 grupos (10 folds), visto en el Cap. 10. A continuación se determina la semilla aleatoria, para que los resultados sean replicables, y se entrena el modelo.
# se fija una semilla aleatoria
set.seed(101)
# se entrena el modelo
model <- train(CLS_PRO_pro13 ~ ., # . equivale a incluir todas las variables
data=dp_entr,
method="rpart",
metric="ROC",
trControl=trControl)model
CART
558 samples
17 predictor
2 classes: 'S', 'N'
No pre-processing
Resampling: Cross-Validated (10 fold)
Summary of sample sizes: 502, 502, 502, 503, 503, 502, ...
Resampling results across tuning parameters:
cp ROC Sens Spec
0.05017921 0.8172123 0.9214286 0.7026455
0.10394265 0.7559406 0.8386243 0.6914021
0.51971326 0.6347222 0.8564815 0.4129630
ROC was used to select the optimal model using the largest value.
The final value used for the model was cp = 0.05017921, where cp is the complexity paramenter.
ggplot(melt(model$resample[,-4]), aes(x = variable, y = value, fill=variable)) +
geom_boxplot(show.legend=FALSE) +
xlab(NULL) + ylab(NULL)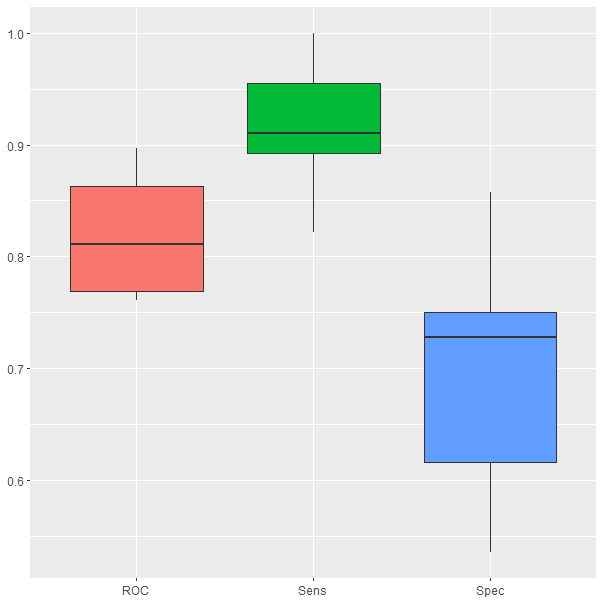
Figura 24.4: Resultados del modelo durante la validación cruzada.
Los resultados de validación cruzada quedan recogidos en los box plots de la Fig. 24.4, por lo que se pueden ver los valores entre los que oscilan las principales medidas de bondad de clasificación en los 10 grupos del proceso de validación. Estas
medidas (ROC, sensibilidad y especificidad) se definieron en el Cap.
10, y en el caso de árboles de clasificación se
utilizan para evaluar el modelo. El árbol generado se muestra en la Fig. 24.5. Se puede observar que este árbol es muy sencillo (téngase en cuenta que se seleccionan las mejores particiones y que las que no aparecen carecen de interés a efectos predictivos) y,
por tanto, fácil de interpretar. En primer lugar decide si
un cliente que compra el smartchwatch fitness comprará el nuevo
producto. En caso de no comprar el smartchwatch fitness (No a
ind_pro15S=1), pero sí la depiladora eléctrica (Yes a
ind_pro12S=1), comprará el tensiómetro digital. Si no compra ninguno
de esos dos productos no comprará el nuevo producto.
Se seleccionan las variables que generan las mejores particiones. Aquellas que no aparecen no generan particiones interesantes a nivel predictivo. Esto también se entiende con la importancia de variables explicada más abajo.
# Gráfico del árbol obtenido
rpart.plot(model$finalModel)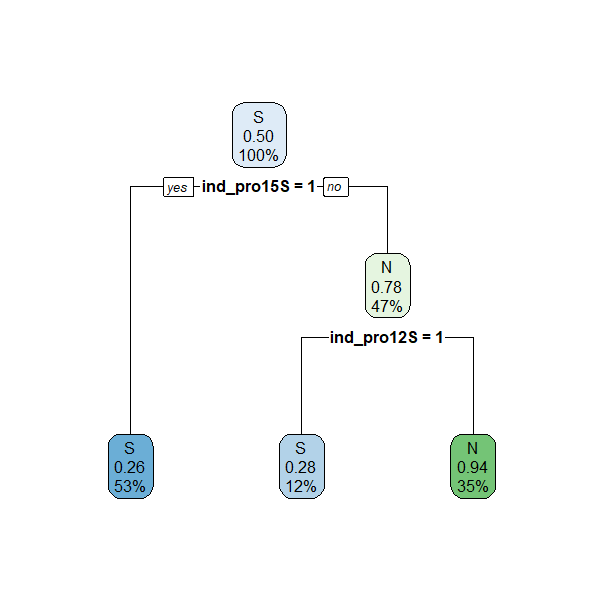
Figura 24.5: Árbol de clasificación sin ajuste automático de hiperparámetros.
Este modelo se puede mejorar ajustando automáticamente
el hiperparámetro188 189
incluido en rpart para el entrenamiento de árboles de decisión. Por consiguiente, primero
es necesario conocer el hiperparámetro a optimizar en el algoritmo
implementado en R que se esté utilizando. Esto se consigue mediante la
siguiente instrucción, incluida en el paquete caret:
modelLookup("rpart")
model parameter label forReg forClass probModel
1 rpart cp Complexity Parameter TRUE TRUE TRUEEl hiperparámetro a optimizar es la complejidad
del árbol, \(\zeta\) (o cp), y se aplica en la fase de
parada durante la construcción del árbol. Como se avanzó anteriormente, esta
fase tiene como función principal evitar divisiones que no
valgan la pena. El hiperparámetro de complejidad \(\zeta\) (o cp en los resultados) puede entenderse como un umbral que permite divisiones (splits) en cada nodo del modelo siempre y cuando haya una mejora mínima en las métricas. Es necesario definir los valores de dicho hiperparámetro que se
quieren evaluar con el objetivo de obtener su valor óptimo.
# Se especifica un rango de valores típicos para el hiperparámetro
tuneGrid <- expand.grid(cp = seq(0.01,0.05,0.01))
# se entrena el modelo
set.seed(101)
model <- train(CLS_PRO_pro13 ~ .,
data=dp_entr,
method="rpart",
metric="ROC",
trControl=trControl,
tuneGrid=tuneGrid)# se muestra la salida del modelo
model
CART
558 samples
17 predictor
2 classes: 'S', 'N'
No pre-processing
Resampling: Cross-Validated (10 fold)
Summary of sample sizes: 502, 502, 502, 503, 503, 502, ...
Resampling results across tuning parameters:
cp ROC Sens Spec
0.01 0.8962254 0.8678571 0.8167989
0.02 0.8663454 0.9000000 0.7667989
0.03 0.8458097 0.9392857 0.7310847
0.04 0.8449381 0.9214286 0.7383598
0.05 0.8172123 0.9214286 0.7026455
ROC was used to select the optimal model using the largest value.
The final value used for the model was cp = 0.01.De forma automática se construyen diversos árboles para cada uno de los
valores explicitados del parámetro de complejdad, \(\zeta\) (denominado cpen los resultados). Para cada uno de esos árboles se obtienen las siguientes correspondientes métricas: el área bajo la
curva ROC (denotada así por las siglas en inglés de receiver operating
characteristic), sensibilidad (Sens) y especificidad (Spec), todas ellas
definidas en el Cap. 10. El valor ROC190 es el utilizado
para la elección del valor óptimo del hiperparámetro de complejidad, por lo que se determina que
finalmente el óptimo es \(cp= \text {0,01}\), puesto que en ese caso el área bajo la curva ROC alcanza el valor máximo: 89,6%. Por tanto, ajustando el hiperparámetro se ha aumentado la
precisión del modelo en casi 8 puntos porcentuales respecto al 81,7% que tenía el modelo
sin ajuste automático de cp.
En la Fig. 24.6 se puede ver el rendimiento de cada una de las métricas del árbol entrenado utilizando validación cruzada. Dicha figura se obtiene con la siguiente instrucción:
ggplot(melt(model$resample[,-4]), aes(x = variable, y = value, fill=variable)) +
geom_violin(show.legend=FALSE) +
xlab(NULL) +
ylab(NULL)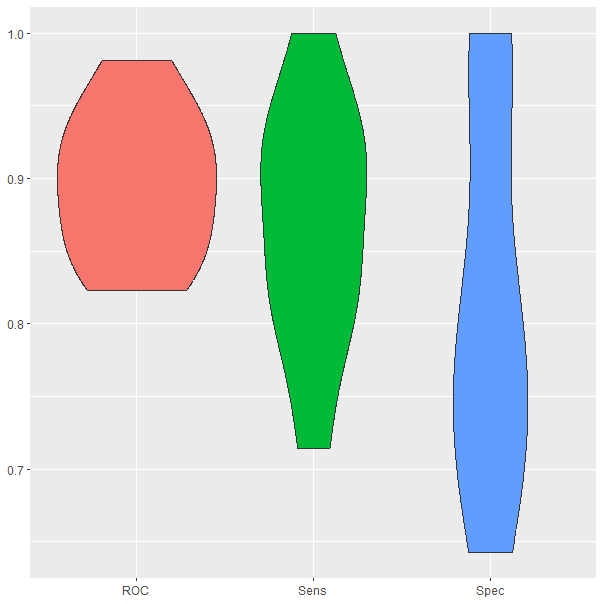
Figura 24.6: Resultados del modelo con ajuste automático durante la validación cruzada.
En la Fig. 24.7 se muestra el árbol generado. La visualización del árbol se obtiene con el siguiente código:
# Gráfico del árbol obtenido
rpart.plot(model$finalModel)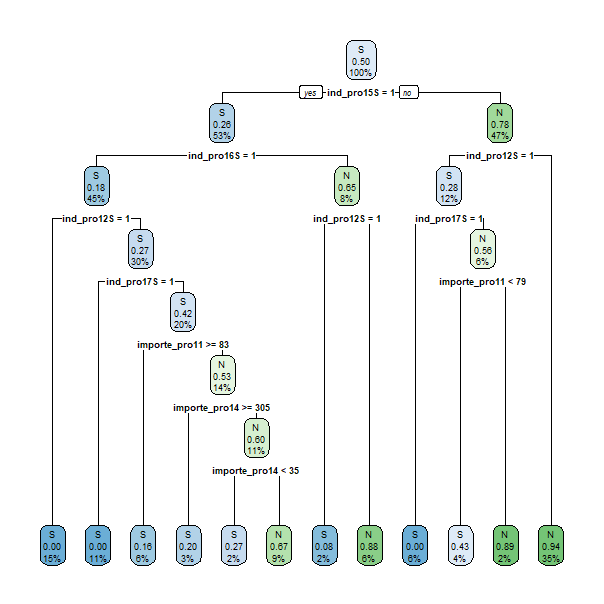
Figura 24.7: Árbol de clasificación con ajuste automático.
Con el objetivo de aumentar la generalidad del árbol y facilitar su interpretación, se procede a reducir su tamaño podándolo. Para ello se establece el criterio de que un nodo terminal tiene que tener, como mínimo, 50 observaciones. El árbol resultante se muestra en la Fig. 24.8.
set.seed(101)
prunedtree <- rpart(CLS_PRO_pro13 ~ ., data=dp_entr,
cp= 0.01, control = rpart.control(minbucket = 50))
rpart.plot(prunedtree)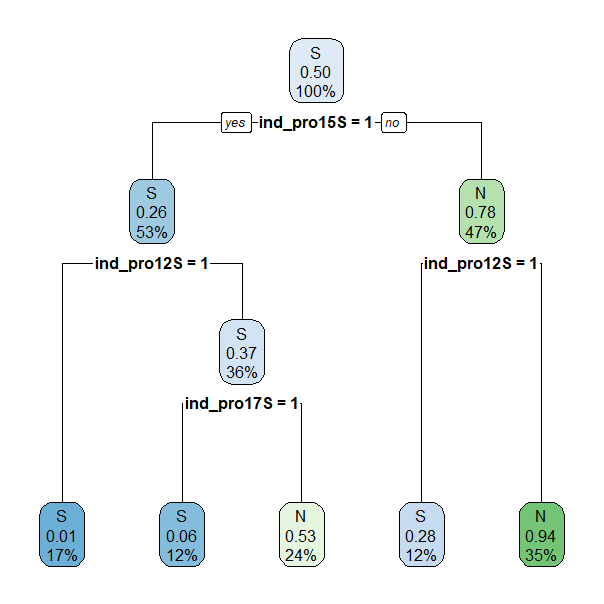
Figura 24.8: Árbol de clasificación con ajuste automático y podado.
Como puede observarse, el número de nodos terminales del árbol se ha reducido considerablemente (de 12 a 5). En tres de ellos el árbol predice que un cliente comprará el nuevo producto si:
Compra el smartwatch fitness (
ind_pro15= S - Yes) y la depiladora eléctrica (ind_pro12= S - Yes).Compra el smartwatch fitness (
ind_pro15= S - Yes) y el estimulador muscular (ind_pro17= S - Yes), pero no la depiladora eléctrica (ind_pro12= S - No).No compra el smartwatch fitness (
ind_pro15= S - No), pero sí la depiladora eléctrica (ind_pro12= S - Yes).
Sin embargo, dos nodos terminales predicen que el cliente no comprará el nuevo producto si:
Compra el smartwatch fitness (
ind_pro15= S - Yes), pero no la depiladora eléctrica (ind_pro12= S - No) ni el estimulador muscular (ind_pro17= S - No).No compra el smartwatch fitness (
ind_pro15= S - No) ni la depiladora eléctrica (ind_pro12= S - No).
24.4 Árboles de regresión
Los árboles de decisión también pueden usarse para resolver problemas de regresión. En este caso, la idea es que la predicción sea un valor numérico en lugar de una categoría. En la Tabla 24.9 se muestran los datos para un problema de regresión equivalente al presentado en las secciones anteriores para clasificación. La variable objetivo (Horas jugadas) ahora es continua en lugar de categórica, como ocurría en el ejemplo de clasificación con la variable Decisión.
| Día | Tipo de día | Humedad | Viento | Horas jugadas |
|---|---|---|---|---|
| 1 | Soleado | Fuerte | Débil | 2,3 |
| 2 | Soleado | Fuerte | Fuerte | 1,5 |
| 3 | Lluvia | Fuerte | Débil | 1,3 |
| 4 | Nublado | Fuerte | Débil | 2,4 |
| 5 | Lluvia | Débil | Débil | 1,9 |
| 6 | Lluvia | Débil | Fuerte | 2,4 |
| 7 | Soleado | Fuerte | Débil | 2,3 |
| 8 | Nublado | Débil | Fuerte | 2,2 |
| 9 | Soleado | Débil | Débil | 1,3 |
| 10 | Lluvia | Débil | Débil | 1,8 |
| 11 | Soleado | Débil | Fuerte | 1,2 |
| 12 | Nublado | Fuerte | Fuerte | 2,9 |
| 13 | Nublado | Débil | Débil | 2,2 |
| 14 | Lluvia | Fuerte | Fuerte | 1,5 |
| 15 | Soleado | Fuerte | Fuerte | 1,5 |
Las principales medidas descriptivas de la variable respuesta (media, varianza, desviación típica y coeficiente de variación) son:
\[\begin{equation} \bar{x}_{\text{Horas jugadas}} = \frac{1}{n}\sum{x} = \text {1,91}, \tag{24.3} \end{equation}\] \[\begin{equation} \sigma^{2}_{\text{Horas jugadas}} = \frac{\sum{(x-\bar{x}\Bigr)^{2}}}{n} = \text {0,25}, \tag{24.4} \end{equation}\] \[\begin{equation} \sigma_{\text{Horas jugadas}} = \sqrt{\sigma^{2}} = \text {0,50}, \tag{24.5} \end{equation}\] \[\begin{equation} CV_{\text{Horas jugadas}} = \frac{\sigma}{\bar{x}} = \text {0,26}. \tag{24.6} \end{equation}\]De ellas, es de especial interés la desviación típica del conjunto de datos, pues en los árboles de regresión las divisiones que se harán en dicho conjunto conducirán a subconjuntos que, cada vez, tienen menor desviación típica.
24.4.1 ¿Cómo se va formando el árbol de regresión?
Mientras que en los árboles de clasificación se utiliza la entropía o la impureza de Gini para medir la homogeneidad de un nodo, en los árboles de regresión se utiliza como métrica la desviación típica \((\sigma)\) de la variable respuesta. Por tanto, cuando se selecciona una variable para hacer la división, se calcula la desviación típica para cada una de las ramas, y se obtiene una media ponderada en función del número de elementos de cada una de ellas:
\[\begin{equation} \sigma_{X} = \sum_{r\in X}{P(r)\cdot\sigma_{r}}, \tag{24.7} \end{equation}\]donde \(X\) es la variable de la cual se quiere obtener la desviación típica (también se podría hablar en términos de conjunto de datos), \(r\) son las ramas y \(P(r)\) es la probabilidad de seleccionar cada una de esas ramas, que se puede estimar mediante el cociente entre el número de observaciones de la rama y el total de las que se consideran en el nodo.
Siguiendo un proceso idéntico al que se ha mostrado en el caso de los árboles de clasificación, para los datos mostrados en la Tabla 24.9), la desviación típica es 0,50 horas jugadas (véase ecuación (24.5), y entre las variables predictoras, Tipo de día, Humedad y Viento, se seleccionará como nodo raíz aquella que genere una partición del conjunto inicial más homogénea (con menos desviación típica ponderada).
Para cada una de las tres variables candidatas a nodo raíz, las desviaciones típicas en los subconjuntos correspondientes a cada una de sus ramas o categorías son las que se indican en las Tablas 24.10, 24.11 y 24.12:
| Tipo de día | # observaciones | \(\sigma_{\text{Horas jugadas}}\) |
|---|---|---|
| Soleado | 6 | 0,45 |
| Nublado | 4 | 0,29 |
| Lluvia | 5 | 0,38 |
| Humedad | # observaciones | \(\sigma_{\text{Horas jugadas}}\) |
|---|---|---|
| Fuerte | 8 | 0,55 |
| Débil | 7 | 0,43 |
| Viento | # observaciones | \(\sigma_{\text{Horas jugadas}}\) |
|---|---|---|
| Fuerte | 7 | 0,57 |
| Débil | 8 | 0,42 |
A partir de las desviaciones típicas en las ramas de cada variable, se obtiene la desviación típica (ponderada) de cada variable de acuerdo a la ecuación (24.7).
La reducción que se opera en la desviación típica de los valores de la variable respuesta del conjunto inicial (diferencia entre la desviación de la variable respuesta y la que se obtiene cuando se divide el conjunto de datos en base a cada una de las variables) puede verse en la Tabla 24.13.
| Variable | \(\sigma_{\text{Horas jugadas}}\) | Reducción |
|---|---|---|
| Tipo de día | 0,38 | 0,12 |
| Humedad | 0,49 | 0,01 |
| Viento | 0,49 | 0,01 |
Dado que la partición del conjunto de datos según la variable Tipo de día es la que produce una mayor reducción en la desviación típica, dicha variable resulta elegida como nodo raíz.
A continuación, se procede a la partición de los subconjuntos de observaciones correspondientes a las ramas de la variable Tipo de día: soleado, nublado y con lluvia en función de Humedad o Viento. Comenzando con Tipo de día: soleado, se tiene que la partición del subconjunto de datos correspondientes a días soleados según la Humedad da lugar a los resultados que se muestran en la Tabla 24.14:
| Humedad | # observaciones | \(\sigma_{\text{Horas jugadas}}\) |
|---|---|---|
| Fuerte | 4 | 0,4 |
| Débil | 2 | 0,05 |
Si la variable de partición fuese la fuerza del Viento, entonces se tendrían los resultados que figuran en la Tabla 24.15:
| Viento | # observaciones | \(\sigma_{\text{Horas jugadas}}\) |
|---|---|---|
| Fuerte | 3 | 0,14 |
| Débil | 3 | 0,47 |
En la Tabla 24.16 se muestra la desviación típica para cada variable (obtenida como media ponderada de las desviaciones típicas correspondientes a sus ramas), así como la reducción de desviación que produce. Como la mayor reducción se produce en Humedad, la siguiente división se realizaría en función de las categorías de esta variable.
| Variable | \(\sigma_{\text{Horas jugadas}}\) | Decremento |
|---|---|---|
| Humedad | 0,28 | 0,17 |
| Viento | 0,31 | 0,14 |
De igual manera se procedería en el caso de días nublados o lluviosos. En el caso de días nublados la desviación típica (ponderada) del número de horas en los subconjuntos de datos que genera la partición por Humedad es 0,2208, mientras la de los subconjuntos que genera la partición por fuerza del Viento es 0,2775 (se dejan al lector estos cálculos), por lo cual la reducción en desviación típica (o el aumento de homogenidad en los valores de la variable respuesta) es mayor cuando se particiona por Humedad. En el caso de los días lluviosos, la partición que da lugar a mayor homogeneidad en los subconjuntos que genera también es la que se lleva a cabo mediante la variable Humedad (la desviación típica ponderada en los subconjuntos de las ramas de Humedad es 0,1975, mientras que la de los subconjuntos generados al particionar por la fuerza del Viento es 0,3375; también se dejan al lector estos cálculos.
24.4.2 ¿Cuánto debe crecer el árbol de regresión?
Como en el caso de los árboles de clasificación, es necesario establecer reglas que pongan fin al proceso de crecimiento del árbol. Además de los criterios de parada que se utilizan en árboles de clasificación (número de elementos mínimos en un nodo y número de niveles máximos en la estructura del árbol), en los árboles de regresión se detiene su crecimiento estableciendo un threshold (umbral de decisión) sobre el coeficiente de variación del nodo. En el ejemplo expuesto en la Tabla 24.17 sobre Horas jugadas, se puede ver qué nodos podrían seguir creciendo si se establece que el árbol continúe creciendo en nodos con un coeficiente de variación de un 15% o más y con al menos 5 observaciones.
| Nodo padre | Rama | CV en nodo hijo | # observaciones |
|---|---|---|---|
| Tipo de día | Nublado | 11,80% | 4 |
| Tipo de día | Lluvia | 21,14% | 5 |
| Humedad | Fuerte | 21,04% | 4 |
| Humedad | Débil | 4,04% | 2 |
En este ejemplo, el árbol seguiría creciendo por la rama Lluvia, donde habría que seleccionar la siguiente variable de división. En el resto de ramas no se supera el número mínimo establecido de observaciones en el nodo y en Nublado y Débil tampoco se alcanza el coeficiente de variación mínimo. Por otra parte, en los árboles de regresión la poda se lleva a cabo del mismo modo que para árboles de clasificación. Igual que en la ecuación (24.2), el error de entrenamiento se mide a través de la suma de los cuadrados de los errores (en inglés sum of squared (estimated) errors, SSE), es decir:
\[\begin{equation} SSE_{\zeta}(\tau) = SSE(\tau) + \zeta|\tau|. \tag{24.8} \end{equation}\]24.4.3 Árbol de regresión para estimar el número de días de hospitalización
En este ejemplo se utilizan los datos cleveland, incluidos en el
paquete CDR, y que han sido utilizados en el Cap. 16 para
estimar la variable Días de hospitalización, dhosp. El conjunto de datos contiene información sobre pacientes que llegan a un hospital con dolor de pecho y de los
cuales se han recogido distintas características. Se pretende predecir
el número de días de hospitalización que necesitará un paciente en base
al resto de características observadas: si
el paciente está diagnosticado de accidente coronario o no, su edad, su sexo,
el tipo de dolor que padece y la depresión en el segmento ST inducida
por ejercicio en relación con el reposo.
# se cargan los datos
data("cleveland")
# se entrena el modelo
set.seed(101)
model <- rpart(dhosp ~ diag + edad + sexo + tdolor + dep,
data=cleveland, method="anova")model$cptable
CP nsplit rel error xerror xstd
1 0.37275022 0 1.0000000 1.0128283 0.09213359
2 0.01674747 1 0.6272498 0.6427926 0.06048143
3 0.01132433 4 0.5770074 0.6788431 0.06681871
4 0.01007684 6 0.5543587 0.6825792 0.06505426
5 0.01000000 7 0.5442819 0.6843192 0.06514439En la salida anterior xerror es el error de validación cruzada, rel error es el xerror reescalado para que el valor máximo sea 1 y xstd es la desviación típica del error de la validación cruzada.
Se observa que para valores muy altos del hiperparámetro de complejidad (cpen los resultados),
SSE es muy elevado. Esto es, produce modelos muy sencillos pero con
nula potencia predictiva. En el otro extremo, para \(\zeta=\text {0,01}\), SSE
se reduce hasta llegar a SSE = 0,54 por lo que el árbol se poda de
acuerdo a la ecuación (24.8) con dicho valor de \(\zeta\). El
resultado del modelo se muestra en el árbol de la Fig.
24.9. La interpretación de este árbol sería:
Si el paciente no tiene diagnóstico de accidente coronario, solo necesitará un día de hospitalización.
En el caso de tener este diagnóstico y una depresión mayor o igual a dos en el segmento ST inducida por ejercicio en relación al reposo, necesitará 2,8 días de hospitalización.
En un último ejemplo, si la depresión en el segmento ST inducida por ejercicio en relación con el reposo está entre 0,35 y 2, entonces el paciente necesitará 3,8 días de hospitalización. Si, por el contrario, la depresión en el segmento ST inducida por ejercicio en relación con el reposo es menor a 0,35, el número de días de hospitalización depende del sexo del paciente: los hombres necesitarán 3,2 días y las mujeres tan solo 1,9 días.
# se pinta el árbol obtenido
rpart.plot(model)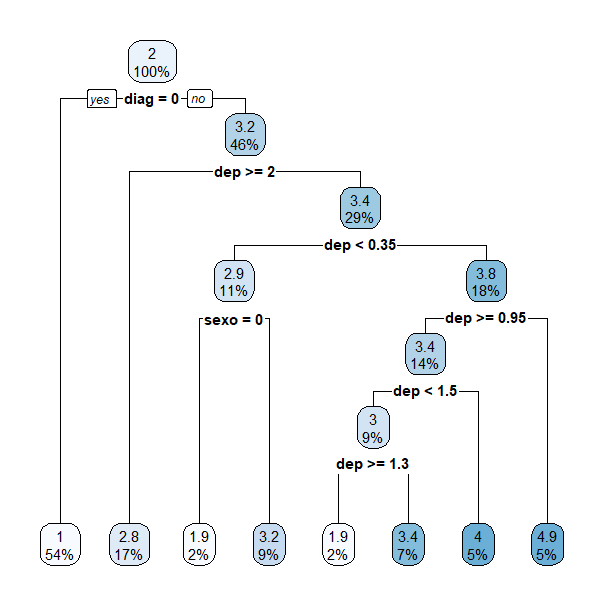
Figura 24.9: Árbol de regresión para predecir el número de días de hospitalización.
24.4.4 Árbol de regresión para la predicción del precio unitario de la vivienda en Madrid
En este ejemplo se entrena un árbol de regresión para predecir el
precio unitario de la vivienda en Madrid. Para ello se utilizan
los datos de viviendas a la venta en Madrid publicados en Idealista
durante el año 2018. Estos datos están incluidos en el paquete
idealista18. Para facilitar la interpretación del modelo, solo se van
a utilizar 8 de las variables incluidas en el conjunto de datos:
superficie construida, número de dormitorios, número de baños, si tiene
terraza, si tiene ascensor, si el precio incluye el parking, distancia
al centro de Madrid y distancia a una parada de metro.
library("idealista18")
data("Madrid_Sale")
Madrid_Sale <- Madrid_Sale |>
dplyr::select(UNITPRICE, CONSTRUCTEDAREA, ROOMNUMBER, BATHNUMBER,
HASTERRACE,HASLIFT, ISPARKINGSPACEINCLUDEDINPRICE,
DISTANCE_TO_CITY_CENTER, DISTANCE_TO_METRO)
head(Madrid_Sale)
UNITPRICE CONSTRUCTEDAREA ROOMNUMBER BATHNUMBER HASTERRACE HASLIFT
1 2680.851 47 1 1 0 1
2 4351.852 54 1 1 0 0
3 4973.333 75 2 1 0 0
4 5916.667 48 1 1 0 1
5 4560.000 50 0 1 0 0
6 3921.260 127 3 2 0 1
ISPARKINGSPACEINCLUDEDINPRICE DISTANCE_TO_CITY_CENTER (km) DISTANCE_TO_METRO (Km)
1 0 8.0584293 0.8720746
2 0 0.8763693 0.1163821
3 0 0.9074793 0.1391088
4 0 0.8454622 0.1442990
5 0 1.2502313 0.3370982
6 0 0.5417727 0.1614363
# Se entrena el modelo
library("rpart")
set.seed(101)
model <- rpart(UNITPRICE ~ ., Madrid_Sale, method = "anova")# se muestra la salida del modelo
model
n= 94815
node, split, n, deviance, yval
* denotes terminal node
1) root 94815 274173500000 3661.052
2) DISTANCE_TO_CITY_CENTER>=3.201972 59706 102376700000 2932.605
4) HASLIFT< 0.5 20515 16728050000 2160.029 *
5) HASLIFT>=0.5 39191 66994050000 3337.019
10) BATHNUMBER< 2.5 34662 55189210000 3212.614
20) ROOMNUMBER>=1.5 29068 40422630000 3080.170 *
21) ROOMNUMBER< 1.5 5594 11607120000 3900.833 *
11) BATHNUMBER>=2.5 4529 7162750000 4289.133 *
3) DISTANCE_TO_CITY_CENTER< 3.201972 35109 86236590000 4899.840
6) DISTANCE_TO_METRO>=0.4584401 4749 9978473000 3873.427 *
7) DISTANCE_TO_METRO< 0.4584401 30360 70472330000 5060.394
14) HASLIFT< 0.5 7293 12520500000 4465.560 *
15) HASLIFT>=0.5 23067 54555510000 5248.461 *Como en el ejemplo anterior, para \(\zeta=\text {0,01}\) SSE se reduce hasta SSE \(=\text {0,56}\), por lo que el árbol se poda de acuerdo a la ecuación (24.8) con dicho valor de \(\zeta\). El resultado del modelo se muestra en el árbol de la Fig. 24.10. La interpretación de este árbol sería:
Si una vivienda con ascensor se encuentra a menos de 3,2 km del centro de Madrid y a menos de 0,46 km de una estación de metro, el precio por metro cuadrado predicho para esa vivienda será de 5.248 €.
Si una vivienda se encuentra a más de 3,2 km del centro de Madrid y no tiene ascensor, el precio predicho será de 2.160 € por metro cuadrado.
Si una vivienda se encuentra a menos de 3,2 km del centro de Madrid y a más de 0,46 km de una estación de metro, el precio unitario predicho para esa vivienda será de 3.873 €/\(\text {m}^{2}\).
Se deja al lector la interpretación de los casos donde, además, se tiene en cuenta el número de baños y de habitaciones.
# se pinta el árbol obtenido
rpart.plot(model)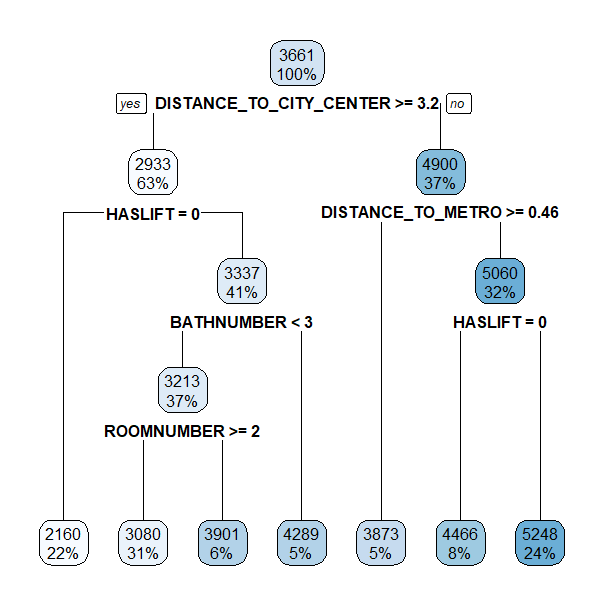
Figura 24.10: Árbol de regresión para predecir el precio por metro cuadrado de las viviendas en Madrid.
Resumen
En este capítulo se introduce al lector en los árboles de decisión para abordar problemas de clasificación y regresión. En particular:
Se muestra la lógica de la construcción de árboles de decisión, ya sean de regresión o clasificación.
Se contemplan diferentes medidas con las que el árbol decide avanzar hacia un nuevo punto de decisión.
Se abordan los conceptos de sobreajuste y complejidad del árbol, así como la forma de controlarlos.
Se muestra el uso de R para la clasificación en clases binarias y para la predicción de variables respuesta numéricas en casos aplicados.