Capítulo 34 Escalamiento multidimensional

José Luis Alfaro Navarro\(^{a}\) y Manuel Vargas Vargas\(^{a}\)

\(^{a}\)Universidad de Castilla-La Mancha

34.1 Introducción

El escalado multidimensional (EMD) fue propuesto por primera vez a la Universidad de Princeton por Warren S. Torgerson a principios de la década de 1950 siendo un investigador importante en este campo Joseph Bernard Kruskal. El EMD engloba una variedad de técnicas multivariantes cuya finalidad es obtener la estructura (factores o dimensiones) de los individuos (o variables) subyacente a una matriz de datos empíricos, lo que se consigue al representar dicha estructura en una forma geométrica bidimensional o tridimensional.

Por tanto, la idea del EMD es representar los datos en baja dimensión (usualmente 2 dimensiones) utilizando la información proporcionada por las distancias entre los datos. Su surgimiento se debió a que el tratamiento de los datos disponibles (y el objetivo de su análisis) hacían difícil su tratamiento con las medidas clásicas, por lo que se fueron diseñando nuevas medidas de distancia entre datos. Estas medidas se pueden utilizar para diferentes tareas: agrupamiento de casos, clasificación, detección de patrones o dimensiones subyacentes, recuperación de información, etc. Por lo tanto, el EMD aborda algunas problemáticas que pueden ser analizadas con otras técnicas como, por ejemplo, el análisis de componentes principales, o el análisis factorial, cuando el objetivo es representar muchas variables en pocas dimensiones mediante la identificación de la estructura interna de los datos, dimensiones o factores en base a la matriz de correlaciones como medida de proximidad entre las variables, o el análisis clúster cuando el objetivo es analizar la proximidad entre objetos, personas, productos, etc.

El EMD analiza matrices de proximidades (similitudes, disimililitudes o distancias y, por ello, es una alternativa más flexible que otros métodos multivariantes con los que comparte objetivos, ya que solo requiere de una matriz con las proximidades entre los datos, que pueden representar valoraciones personales, grado de acuerdo entre juicios, parecido entre objetos, frecuencias de aparición de rasgos, diferencias entre tratamientos, etc. La idea central es que las distancias que median entre los puntos se corresponden con las proximidades entre los objetos por medio de una función de ajuste resultante de un proceso iterativo de optimización, pudiendose describir las relaciones entre los objetos sobre la base de las proximidades observadas (López-Gónzalez & Hidalgo-Sánchez, 2010).

En R existen distintas funciones para desarrollar el EMD: desde las clásicas funciones cmdscale() del paquete base e isoMDS() del paquete MASS hasta el enfoque más actual, usado en este manual y recogido en el paquete smacof (De Leeuw & Mair, 2009; Mair et al., 2022), que proporciona al usuario una gran flexibilidad a la hora de su especificación. Utiliza siempre matrices de disimilaridad y, desde su primera versión, se han implementado varios enfoques de la técnica (y sus correspondientes despliegues), así como varias extensiones y funciones de utilidad.

A modo de ejemplo, se usa la información relacionada con 7 variables de la sociedad de la información disponibles para 27 países europeos en la base de datos TIC2021, cuatro relacionadas con el uso de las TIC por parte de las empresas y tres de aspectos relacionados con el uso por parte de las personas y la equipación de los hogares. Dicha información, así como la descripción de las variables, puede consultarse en la base de datos TIC2021 del paquete CDR.

34.2 Medición de distancias y similitudes

El concepto de distancia, entendida como medida de diferenciación entre objetos, constituye la base fundamental de la obtención y presentación de los resultados del EMD (y de muchas otras técnicas multivariantes). También son frecuentes los conceptos de “disimilaridad”, muy parecido al de distancia, o de “similaridad”, dual en su sentido al de distancia. Se nombre como se nombre, la característica que hay que tener siempre presente es si la medida indica “alejamiento” entre los objetos (distancia o disimilaridad) o “cercanía” (similaridades o proximidades).

Básicamente, se considera una medida de distancia, en un espacio de \(p\) dimensiones, a una función que asigna a cada par de objetos, individuos, productos o lo que sea que se esté estudiando (\(x_u\) y \(x_v\)),²⁴¹ un número real, \(d(x_u, x_v)=\delta_{uv}\), que debe cumplir las siguientes condiciones (para un análisis más detallado véase Sec. 30.3):

1. No negatividad \(\delta_{u,v} \geq 0\).
2. Simetría, \(\delta_{uv} = \delta_{vu}\).
3. Identificación del objeto, \(\delta_{uu}=0\).

Si, además, es semidefinida positiva y cumple la desigualdad triangular se dice que \(\delta\) es una distancia métrica.

Aunque no se va a profundizar en ello, existen diferencias matemáticas en los requisitos que debe cumplir una medida para ser considerada una distancia o una distancia métrica, así como las condiciones para ser considerada una similaridad. Básicamente, se considera una medida de similaridad a una aplicación que asigna a cada par de objetos (\(x_u\) y \(x_v\)) un número real, \(s_{uv}\), que cumple las mismas condiciones que la distancia salvo la condición c, para la que tiene que cumplir que \(s_{uv} \leq s_{uu}\) y \(s_{uv} \leq s_{vv}\).

Esta condición es más difícil de cumplir, y por ello son más populares las medidas de distancia, al ser más sencillo formular la propiedad c, pues simplifica mucho el poder atribuir un valor de referencia cero para definir la distancia de un individuo a sí mismo. La similitud carece de este valor de referencia, siendo posible que la similitud de un individuo a sí mismo sea diferente de unos a otros. A pesar de esta dificultad, las medidas de similitud surgen de modo natural en muchos problemas relacionados con valoraciones subjetivas de similitud.

Para un conjunto finito de \(N\) objetos, la matriz de similaridades viene dada por:

\[\begin{equation} \textbf{S}= \begin{pmatrix} s_{11} & s_{12} & \dotsb & s_{1N}\\ s_{21} & s_{22} & \dotsb & s_{2N}\\ \vdots & \vdots & \ddots & \vdots\\ s_{N1} & s_{N2} & \dotsb & s_{NN}\\ \end{pmatrix}. \tag{34.1} \end{equation}\]

El paso de una medida de similaridad (\(s_{uv}\)) a una distancia (\(\delta_{uv}\)) se puede hacer de diversas formas. Las más usuales son:

1. \(\delta_{uv} = 1-s_{uv}\).

2. \(\delta_{uv} = \sqrt{1-s_{uv}}\).

3. Si los valores de la diagonal de \(S\) no son la unidad, \(\delta_{uv} = \sqrt{s_{uu}+s_{vv}-2s_{uv}}\).

En general, cuando las características que se miden sobre los objetos son variables cuantitativas \(p\)-dimensionales, las distancias más usadas son la euclídea, la city block, la de Minkowski o la de Mahalanobis (véase Sec. 30.3).

Cuando las variables son binarias (0 y 1), los coeficientes de similaridad más utilizados son el coeficiente de Jaccard o el de Sokal-Sneath; por último, en el caso más general en el que existan variables cuantitativas, binarias y/o cualitativas, se suele utilizar la distancia de Gower (véase Sec. 30.3).

Como se aprecia, las características de los datos que se quieren analizar influyen determinantemente en qué tipo de medida de proximidad utilizar. A su vez, la elección de una medida concreta puede modificar la configuración de los datos y, consecuentemente, los resultados de los análisis que se hagan a partir de ellos.

34.3 Modelo de escalamiento multidimensional

El EMD parte de una matriz de proximidades entre \(N\) objetos:²⁴²

\[\begin{equation} \boldsymbol{\Delta}_{N \times N}= \begin{pmatrix} \delta_{11} & \delta_{12} & \dotsb & \delta_{1N}\\ \delta_{21} & \delta_{22} & \dotsb & \delta_{2N}\\ \vdots & \vdots & \ddots & \vdots\\ \delta_{N1} & \delta_{N2} & \dotsb & \delta_{nN}\\ \end{pmatrix}, \tag{34.2} \end{equation}\]

y busca una representación de los \(N\) objetos en un espacio de menor dimensión, \(k\).

Por consiguiente, el conjunto de datos original:

\[\begin{equation} \mathbf{X}_{N \times p}= \begin{pmatrix} x_{11} & x_{21} & \dotsb & x_{p1}\\ x_{12} & x_{22} & \dotsb & x_{p2}\\ \vdots & \vdots & \ddots & \vdots\\ x_{1N} & x_{2N} & \dotsb & x_{pN}\\ \end{pmatrix} \tag{34.3} \end{equation}\]

se reduce a:

\[\begin{equation} \mathbf{X}_{N \times k}= \begin{pmatrix} x_{11} & x_{21} & \dotsb & x_{k1}\\ x_{12} & x_{22} & \dotsb & x_{k2}\\ \vdots & \vdots & \ddots & \vdots\\ x_{1N} & x_{2N} & \dotsb & x_{kN}\\ \end{pmatrix}, \tag{34.4} \end{equation}\]

de forma que, en este nuevo espacio de k dimensiones se puede calcular la distancia euclídea entre cada par de objetos, \({\bf x}_u\) y \({\bf x}_v\), como sigue:

\[\begin{equation} d_{uv}=\sqrt{\displaystyle\sum_{m=1}^{k}{(x_{um} - x_{vm})^2}}, \hspace{0,5cm} m=1,2,...,k, \tag{34.5} \end{equation}\]

y, construir una matriz de distancias “reproducidas”:

\[\begin{equation} \mathbf{D}_{N \times N}= \begin{pmatrix} d_{11} & d_{12} & \dotsb & d_{1N}\\ d_{21} & d_{22} & \dotsb & d_{2N}\\ \vdots & \vdots & \ddots & \vdots\\ d_{N1} & d_{N2} & \dotsb & d_{NN}\\ \end{pmatrix} \tag{34.6} \end{equation}\]

que aproxime, en la medida de lo posible, a la matriz de proximidades, \(\boldsymbol{\Delta}\).

El concepto básico del EMD es que las distancias entre los objetos en la configuración \({\bf X}_{N \times N}\), \(d_{uv}\) deben corresponder a las proximidades originales, \(\delta_{ij}\), mediante una transformación, \(d_{uv}=f(\delta_{uv})\), donde \(f\) es de algún tipo determinado.

En la práctica no se suele encontrar un ajuste perfecto, por lo que existe un cierto grado de error. Por ello, se define el Stress de Kruskal como una medida de la bondad de ajuste del modelo:

\[\begin{equation} Stress= \sqrt{\frac {\sum_{u,v=1}^N {(f(\delta_{uv})-d_{uv})^2}}{\sum_{u,v=1}^N d_{uv}^2}}. \tag{34.7} \end{equation}\]

En caso de un ajuste perfecto el Stress sería 0, aumentando conforme más grandes sean los errores (diferencias entre las distancias “reproducidas” y las originales). Así, la solución proporcionada por el EMD será “mejor” cuanto más pequeña sea la medida del Stress. También es frecuente utilizar una variante, llamada S-Stress, definida como:

\[\begin{equation} S-Stress= \sqrt{\frac {\sum_{u,v=1}^N {(f(\delta_{uv})^2-d_{uv}^2)^2}}{\sum_{u,v=1}^N (d_{uv}^2)^2}}. \tag{34.8} \end{equation}\]

Otra medida que se suele utilizar como grado de ajuste es el coeficiente de correlación al cuadrado (RSQ), que indica la proporción de variabilidad de los datos explicada por el modelo:

\[\begin{equation} RSQ=\frac{[\sum_{u,v=1}^N {(d_{uv}-d_{..})(f(\delta_{uv})-f(\delta_{..}))}]^2}{[\sum_{u,v=1}^N {(d_{uv}-d_{..})^2][\sum_{u,v=1}^N {(f(\delta_{uv})-f(\delta_{..}))}^2]}}. \tag{34.9} \end{equation}\]

Su valor oscila entre 0 y 1, y se interpreta de forma contraria a las medidas de Stress: cuanto mayor sea el RSQ, mejor ajuste del modelo.

34.4 Tipos de escalamiento multidimensional

La elección de la función \(f\) que relaciona las proximidades originales y las distancias “reproducidas” produce dos tipos básicos de EMD, el EMD métrico (o clásico) y el EMD no métrico. En el primero se considera que los datos están medidos en escala de intervalo o de razón y existe una relación funcional entre las distancias originales y las reproducidas. El segundo se suele aplicar cuando los datos están en escala ordinal o no se asume una relación funcional entre las distancias originales y las reproducidas, sino que solo se conserva su ordenación.

34.4.1 Escalado multidimensional métrico

En el modelo de escalamiento métrico se asume que la relación entre las proximidades y las distancias es de tipo lineal, \(d_{uv}=a+b \delta_{uv}\). De esta forma, se conserva la métrica de distancia original entre objetos lo mejor posible; esta forma de EMD resulta adecuada cuando se trabaja con variables cuantitativas (como se avanzó anteriormente). También se conoce como EMD clásico o como análisis de coordenadas principales.

En el ejemplo que se utiliza en este capítulo para ilustrar la técnica (uso de las TIC en los países de la UE-27), se aplica un EMD métrico con un doble objetivo: por un lado se usa la matriz de correlaciones entre las variables con el objetivo de analizar la similitud entre las mismas y, por otro, se determina la distancia entre los objetos (en este caso los países europeos) para analizar la similitud entre ellos.

En el primer caso, los “objetos” son las siete variables de la base de datos TIC2021 y se utiliza como medida de proximidad (similitud) el coeficiente de correlación entre dichas variables (dos a dos), por lo que se plantea un EMD métrico.

library("smacof")
library("CDR")
correlacion<- cor(TIC2021)
round(correlacion[1:3,],3)
#>           ebroad esales esocmedia  eweb hbroad hiacc  iuse
#> ebroad     1.000  0.377     0.587 0.704  0.422 0.521 0.632
#> esales     0.377  1.000     0.542 0.585  0.167 0.195 0.479
#> esocmedia  0.587  0.542     1.000 0.698  0.567 0.609 0.756

Los pasos a seguir son:

1. Calcular la matriz de disimilaridades sobre la que actúa el paquete smacof(). Para ello, la matriz de correlaciones entre las variables se transforma en una matriz de disimilaridades mediante la función sim2diss(). La conversión de similaridades (correlaciones) en disimilaridades se lleva a cabo por el método “corr”, que utiliza la expresión general \(\delta_{uv} = 1-s_{uv}\). Existen otros métodos en la función sim2diss() para cuando la matriz de proximidades no sea de correlaciones. El argumento to.dist=TRUE permite convertir el resultado en un objeto de la clase dist.

datos<-sim2diss(correlacion,method="corr",to.dist=TRUE)

2. Una vez en disposición de la matriz de disimilaridades, se procede con el EMD métrico mediante la función mds(), versión equivalente a la función smacofSym().

res<-mds(datos,ndim=2,type="ratio")
res
#> 
#> Call:
#> mds(delta = datos, ndim = 2, type = "ratio")
#> 
#> Model: Symmetric SMACOF 
#> Number of objects: 7 
#> Stress-1 value: 0.161 
#> Number of iterations: 42

La Fig. 34.1 representa los siete objetos en dos dimensiones según sus distancias “reproducidas”. Muestra, por tanto, la configuración final de los siete objetos:

plot(res)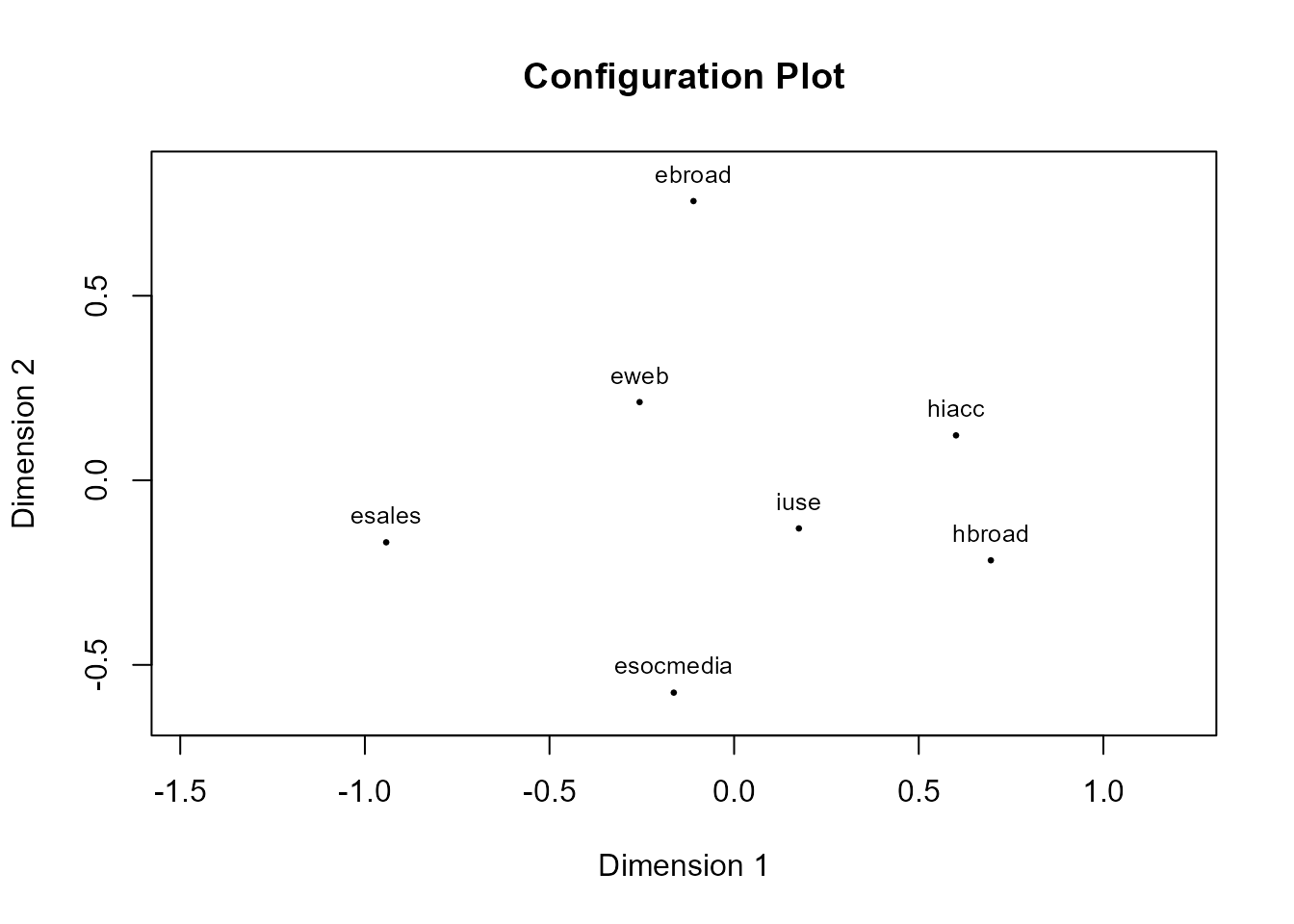

Figura 34.1: Gráfico de objetos en el plano de las distancias reproducidas.

La información numérica detallada se puede obtener con la información de la salida dada por: res$conf, que muestra las coordenadas de los objetos en las dos dimensiones; res$confdist, que proporciona la matriz de distancias reproducidas; res$stress, que aporta la medida de Stress de Kruskal ; y res$spp, que genera la contribución porcentual de cada objeto al Stress.

En este caso, los resultados muestran que la medida de Stress es razonablemente baja (su valor es de 0,16), indicando una buena “reproducción” de las proximidades originales con tan solo dos dimensiones. Además, la “contribución” relativa al Stress de cada uno de los objetos (las siete variables de la base de datos TIC2021) es bastante homogénea, siendo la variable porcentaje de empresas con banda ancha (EBROAD) la que más contribuye al Stress y el nivel de acceso a Internet de los hogares (HIACC) la que menos. El grado de ajuste se puede ver, gráficamente, mediante el gráfico de Shepard (Fig. 34.2), que compara las proximidades originales y las distancias obtenidas.

plot(res,plot.type="Shepard")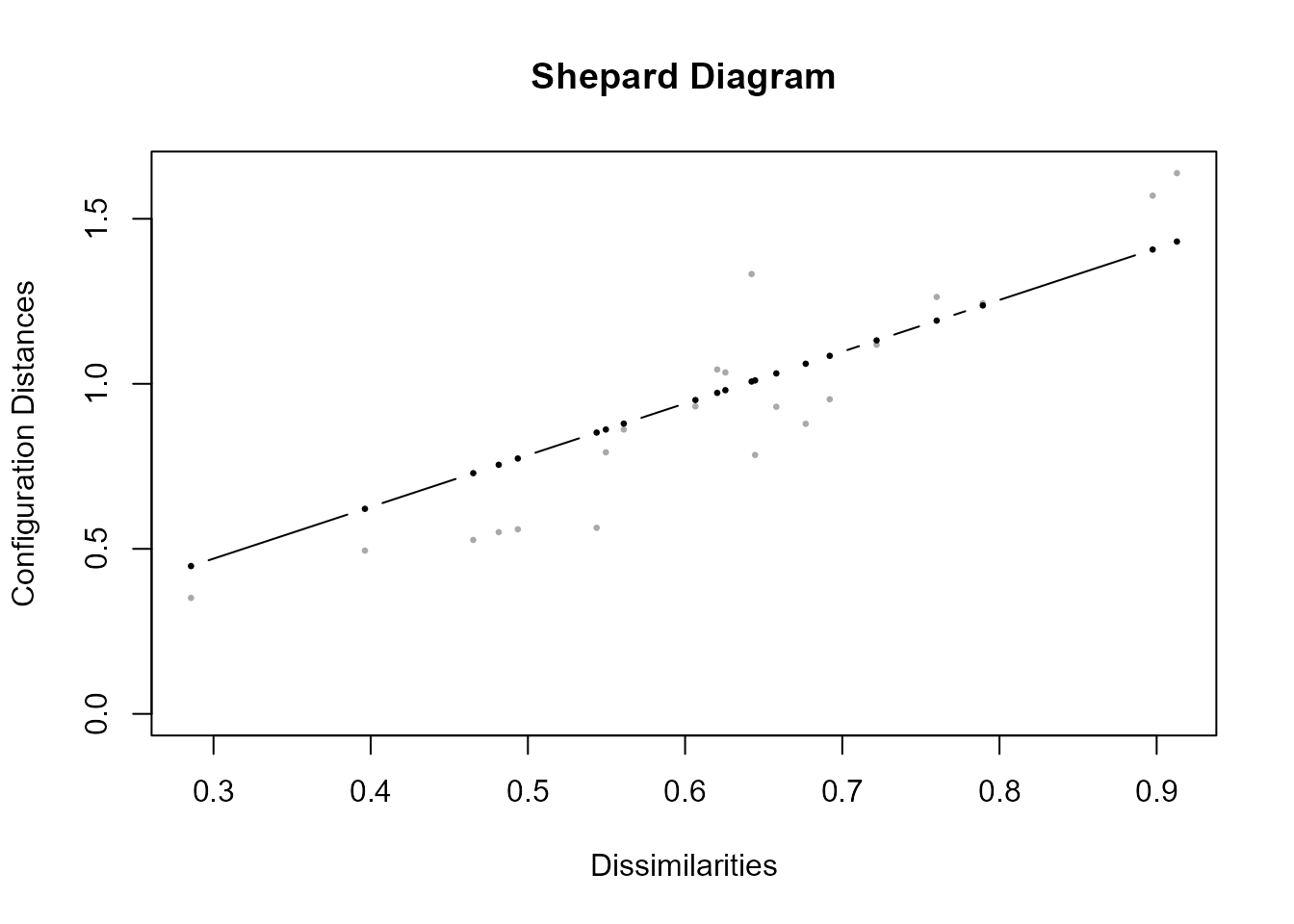

Figura 34.2: Gráfico de Shepard con el método ratio.

El diagrama de Shepard incluye (en gris claro) las proximidades originales entre los 21 pares distintos de objetos (en este caso países) y las obtenidas por el EMD (en negro). Al utilizarse el argumento method=“ratio” se impone una relación proporcional entre ambos tipos de proximidades, por lo que en la figura aparece una recta (que pasa por el origen).²⁴³ Dadas las diferencias que se ven en el gráfico, quizás la elección del método ratio (opción por defecto) no sea la más adecuada. Con el método interval, que impone una relación lineal entre ambos tipos de similitudes (recta que no tiene que pasar necesariamente por el origen) se obtiene la Fig. 34.3.²⁴⁴

res2<-mds(datos, type="interval")
plot(res2, plot.type="Shepard")

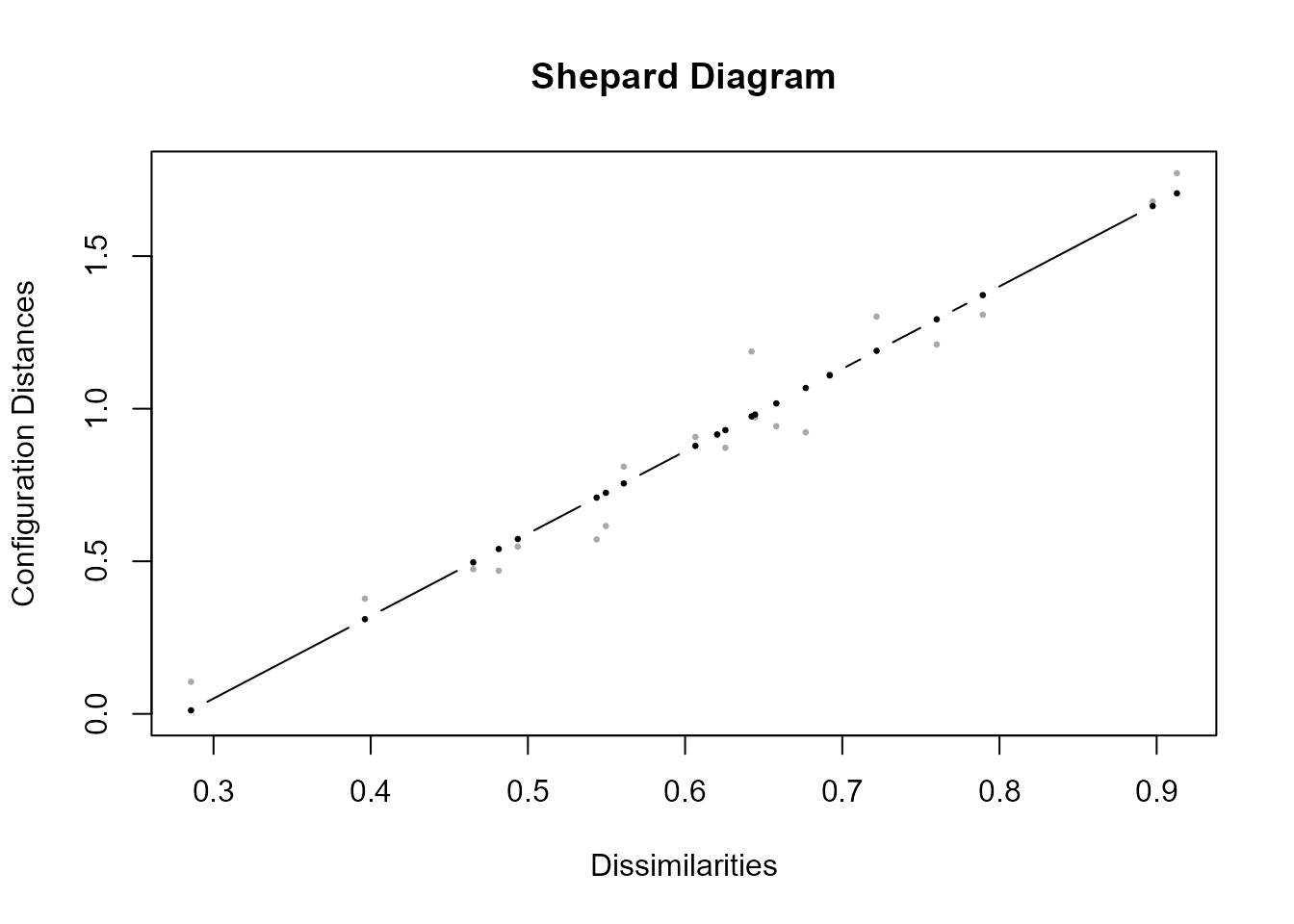
Figura 34.3: Gráfico de Shepard con el método \(interval\).

La medida de Stress se ha reducido a la mitad, 0,087, indicando mejor ajuste, y el gráfico de Shepard muestra más concordancia entre las proximidades originales de los pares de objetos y las distancias reproducidas. Otra opción sería usar el método pmspline, que en este caso no reduce las diferencias, por lo que se opta por method=interval. Los tres métodos son métricos, puesto que se fija una forma funcional para relacionar las proximidades originales y las disimilitudes del modelo (una ratio, una función lineal o una función spline).

• Por último, para “interpretar” el sentido de las dimensiones en las que se representan los objetos, se recurre a ver cuáles están en los extremos. En la parte izquierda de la dimensión 1 están las variables relacionadas con el uso en las empresas, mientras que en la parte derecha están las relacionadas con los hogares y las personas; se podría decir, entonces, que es una dimensión relacionada con el ámbito de uso de las TIC. En la dimensión 2, con menos distancias, y una interpretación menos clara, aparecen en la parte superior las variables relacionadas con el tipo de conexión y la existencia de web en las empresas, y en la parte inferior las relacionadas con las redes sociales, las ventas o la frecuencia de uso de Internet por parte de los individuos; se podría decir que es una dimensión asociada al uso dado a las TIC.

Los pasos para desarrollar el mismo análisis agrupando países, es decir, objetos u observaciones en lugar de variables, serían similares, pero usando la matriz de distancias en lugar de la matriz de correlaciones. Por lo tanto:

library("factoextra")
d_euclidea <- get_dist(x = TIC2021, method = "euclidea")
res3<-mds(d_euclidea,ndim=2,type="ratio")
res3
#> 
#> Call:
#> mds(delta = d_euclidea, ndim = 2, type = "ratio")
#> 
#> Model: Symmetric SMACOF 
#> Number of objects: 27 
#> Stress-1 value: 0.112 
#> Number of iterations: 77

plot(res3)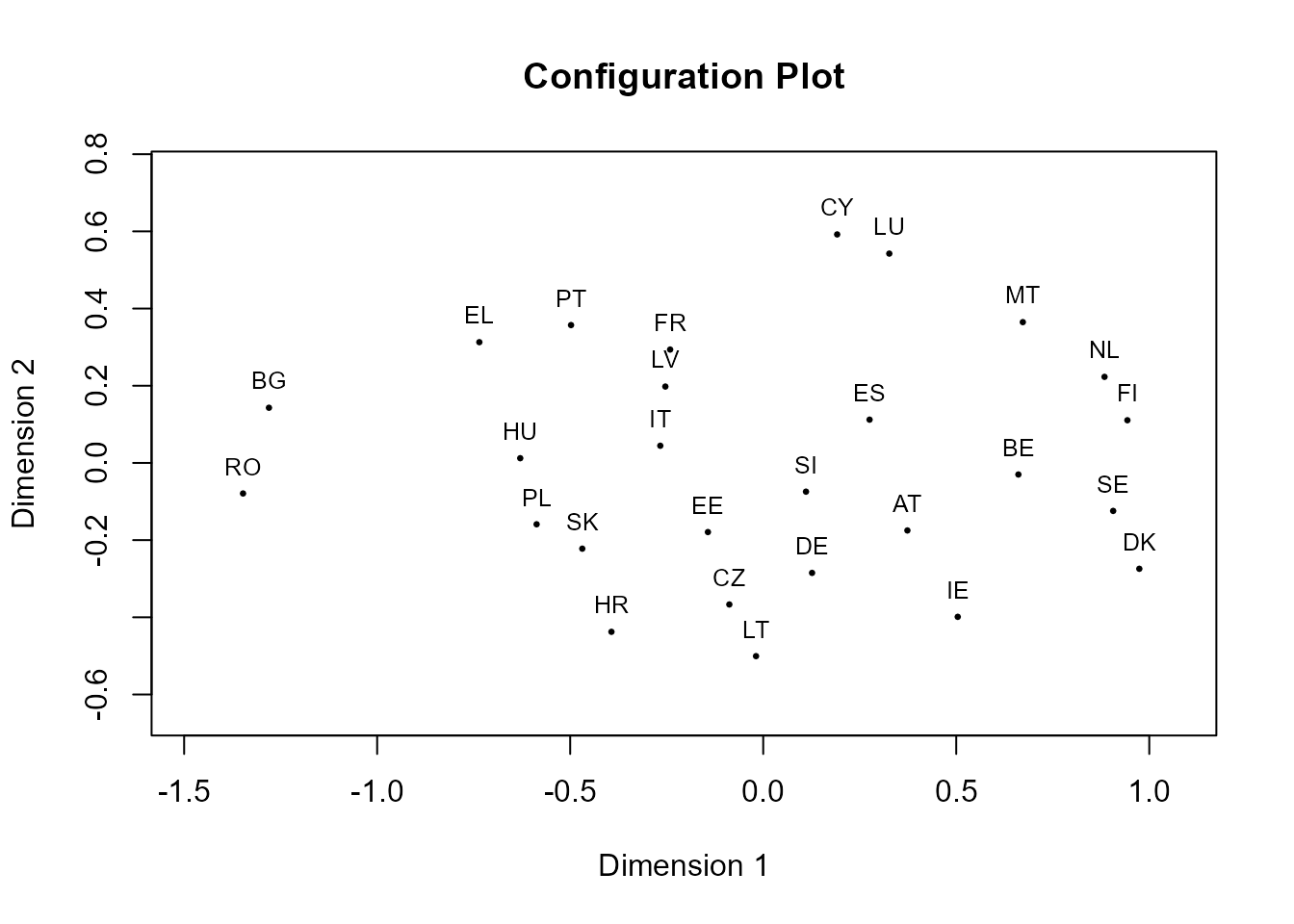

Figura 34.4: Gráfico de países sobre el plano de las distancias reproducidas.

En la Fig. 34.4, la interpretación de la dimensión 1 muestra la existencia de una diferencia clara entre los países del norte y los de última adhesión a la Unión Europea, mientras que en la dimensión 2, con unas diferencias menores, aparecen en la parte superior Chipre y Luxemburgo y en la parte inferior Lituania, Croacia, Irlanda y la República Checa.

34.4.2 Escalado multidimensional no métrico

El modelo de escalamiento no métrico (también conocido como EMD ordinal) no asume ninguna fórmula métrica que relacione las proximidades originales con las distancias reproducidas, sino que solo describe un patrón creciente (o decreciente) entre ellas. El valor de distancia entre un par de objetos no importa; lo que importa es su relación con las distancias entre otros pares de objetos, por lo que construye distancias ajustadas que están en el mismo orden de rango que la proximidad original. Por ejemplo, si la distancia entre los objetos A y B ocupa el tercer lugar en los datos de proximidades originales ordenadas, entonces también debería ocupar el tercer lugar en los datos de distancias reproducidas ordenadas. Así, el EMD no métrico busca conservar no tanto los valores de las proximidades originales, sino la ordenación de los objetos en función de dichas proximidades; es, por tanto, un modelo que se ajusta mejor a datos cualitativos que el métrico, aunque también se utiliza cuando se busca mayor flexibilidad en el ajuste.

A continuación se aplica un EMD no métrico a la matriz de correlaciones de las tasas anuales de siete delitos en 50 estados de EE. UU. (asesinatos, violaciones, robos, asaltos, allanamiento de morada, hurtos y sustracciones de vehículos). Los datos están disponibles en la librería smacof bajo el nombre de crimes:

data("crimes")

En este ejemplo los “objetos” son los siete tipos de delito, y se ha utilizado como medida de proximidad (similitud) el coeficiente de correlación entre las tasas de delito (variables cuantitativas).

• El primer paso consiste en calcular la matriz de disimilaridades sobre la que actúa smacof, utilizando la función sim2diss().

options(digits=3)
data<-sim2diss(crimes,method="corr",to.dist=FALSE)
data
#>            Murder  Rape Robbery Assault Burglary Larceny Auto.Theft
#> Murder      0.000 0.693   0.812   0.436    0.849   0.970      0.943
#> Rape        0.693 0.000   0.671   0.548    0.566   0.632      0.748
#> Robbery     0.812 0.671   0.000   0.663    0.616   0.748      0.616
#> Assault     0.436 0.548   0.663   0.000    0.693   0.825      0.819
#> Burglary    0.849 0.566   0.616   0.693    0.000   0.447      0.548
#> Larceny     0.970 0.632   0.748   0.825    0.447   0.000      0.671
#> Auto.Theft  0.943 0.748   0.616   0.819    0.548   0.671      0.000

La conversión de similaridades (correlaciones) en disimilaridades se realiza con el método corr, que utiliza la expresión general \(\delta_{uv} = \sqrt {1-s_{uv}}\). Existen otros métodos en la función sim2diss() para cuando la matriz de proximidades no sea de correlaciones. El argumento to.dist=TRUE permite convertir el resultado en un objeto de la clase dist si fuese necesario.

Frente a los métodos métricos, que fijan una forma funcional para relacionar las proximidades originales y las disimilitudes del modelo (una ratio, una función lineal o una función spline), una alternativa más flexible es asumir una relación no métrica, donde solo se conserve la ordenación de las proximidades originales. En este caso, se busca que las distancias reproducidas ordenen los pares de objetos de forma idéntica a la original.

Para ello, se utiliza el método ordinal dentro de la función mds():

res4<-mds(data,ndim=2,type="ordinal")
res4
#> 
#> Call:
#> mds(delta = data, ndim = 2, type = "ordinal")
#> 
#> Model: Symmetric SMACOF 
#> Number of objects: 7 
#> Stress-1 value: 0.002 
#> Number of iterations: 15

La Fig. 34.5, obtenida con la función permtest(), representa la relación entre los niveles de Stress y el p-valor asociado a la significación estadística del ajuste. En el ejemplo, la medida de Stress es muy baja (0,002) y significativa para los niveles de significación habituales, indicando un muy buen ajuste.

ptestnm<-permtest(res4,nrep=50)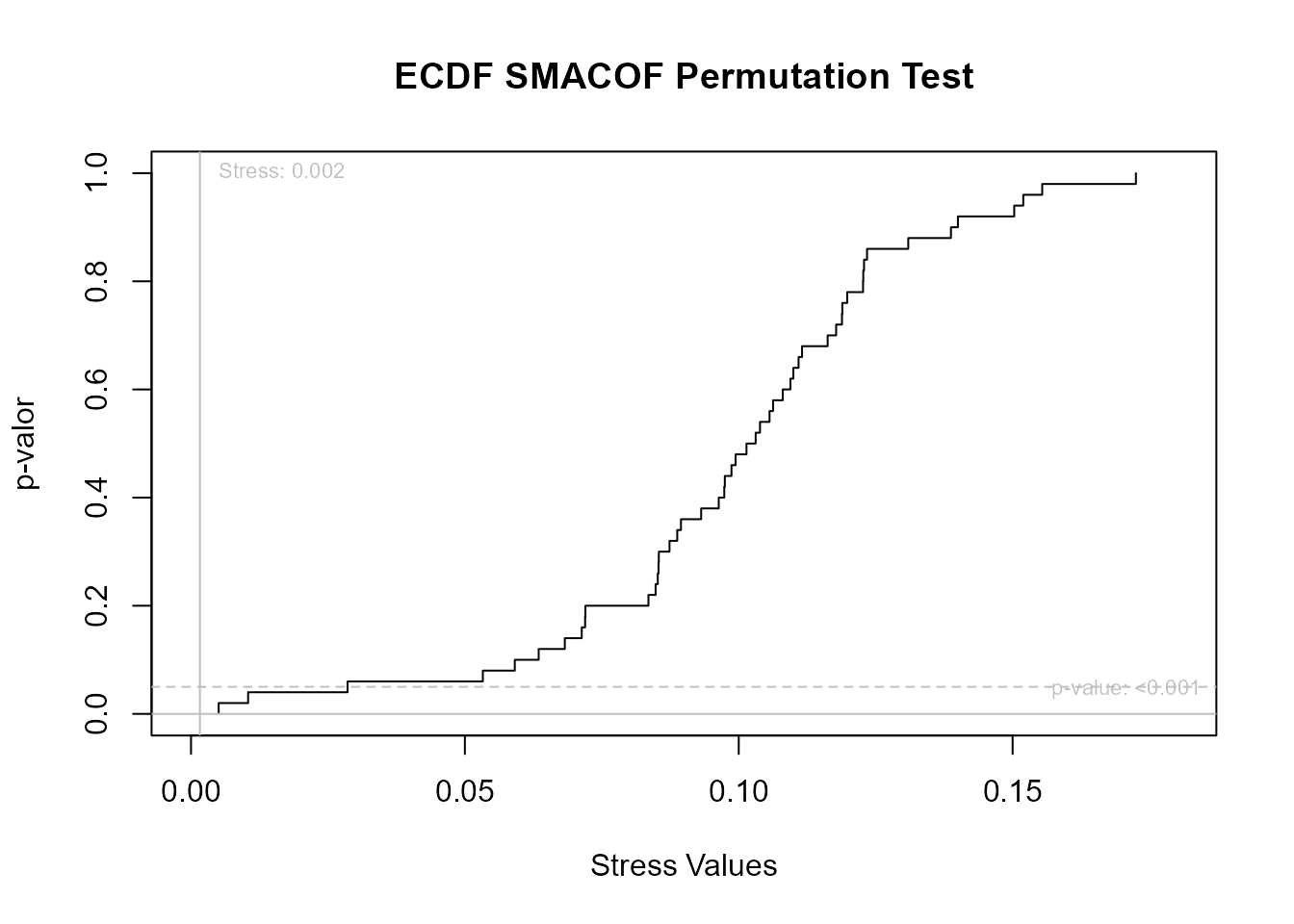

plot(ptestnm, xlim=c(0, 0.18), ylab="p-valor")

Figura 34.5: Test de permutaciones para evaluación de la significatividad de la medida de Stress.

El gráfico de Shepard, representado en la Fig. 34.6, incluye las proximidades originales entre pares de objetos (en gris claro) y las obtenidas por el EMD (en negro), mostrando una alta concordancia entre las ordenaciones original y reproducida:

plot(res4,plot.type="Shepard")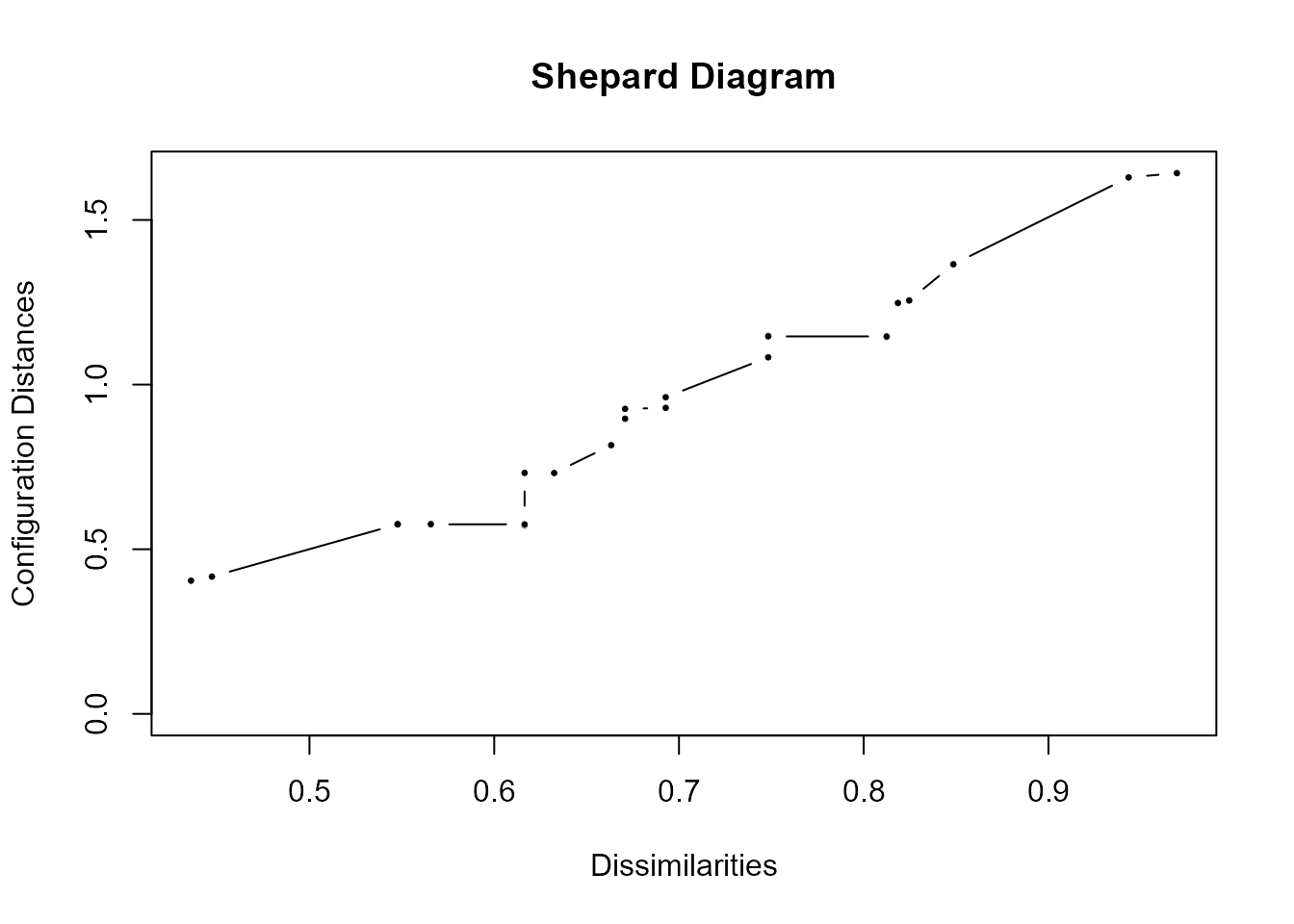

Figura 34.6: Gráfico de Shepard: concordancia entre las ordenaciones original y reproducida.

La contribución porcentual de cada delito a la medida de Stress y las coordenadas bidimensionales reproducidas son:

res4$spp #Contribución porcentual de cada objeto al Stress
#>     Murder       Rape    Robbery    Assault   Burglary    Larceny Auto.Theft 
#>      8.064      6.443     39.270      0.104     10.618      9.023     26.478
res4$conf #Coordenadas de los objetos en dos dimensiones
#>                 D1       D2
#> Murder     -0.9673  0.01136
#> Rape       -0.1225 -0.37592
#> Robbery     0.0496  0.53424
#> Assault    -0.5630 -0.00483
#> Burglary    0.3925 -0.11326
#> Larceny     0.6015 -0.47400
#> Auto.Theft  0.6093  0.42240

Los delitos de robo (39,27%) y de sustracción de vehículos (26,48%) son responsables del 65,75% del Stress, seguidos muy de lejos por los otros cinco tipos de delito.

La Fig. 34.7 muestra la representación bidimensional de la configuración final de los siete delitos según sus distancias “reproducidas”:

plot(res4)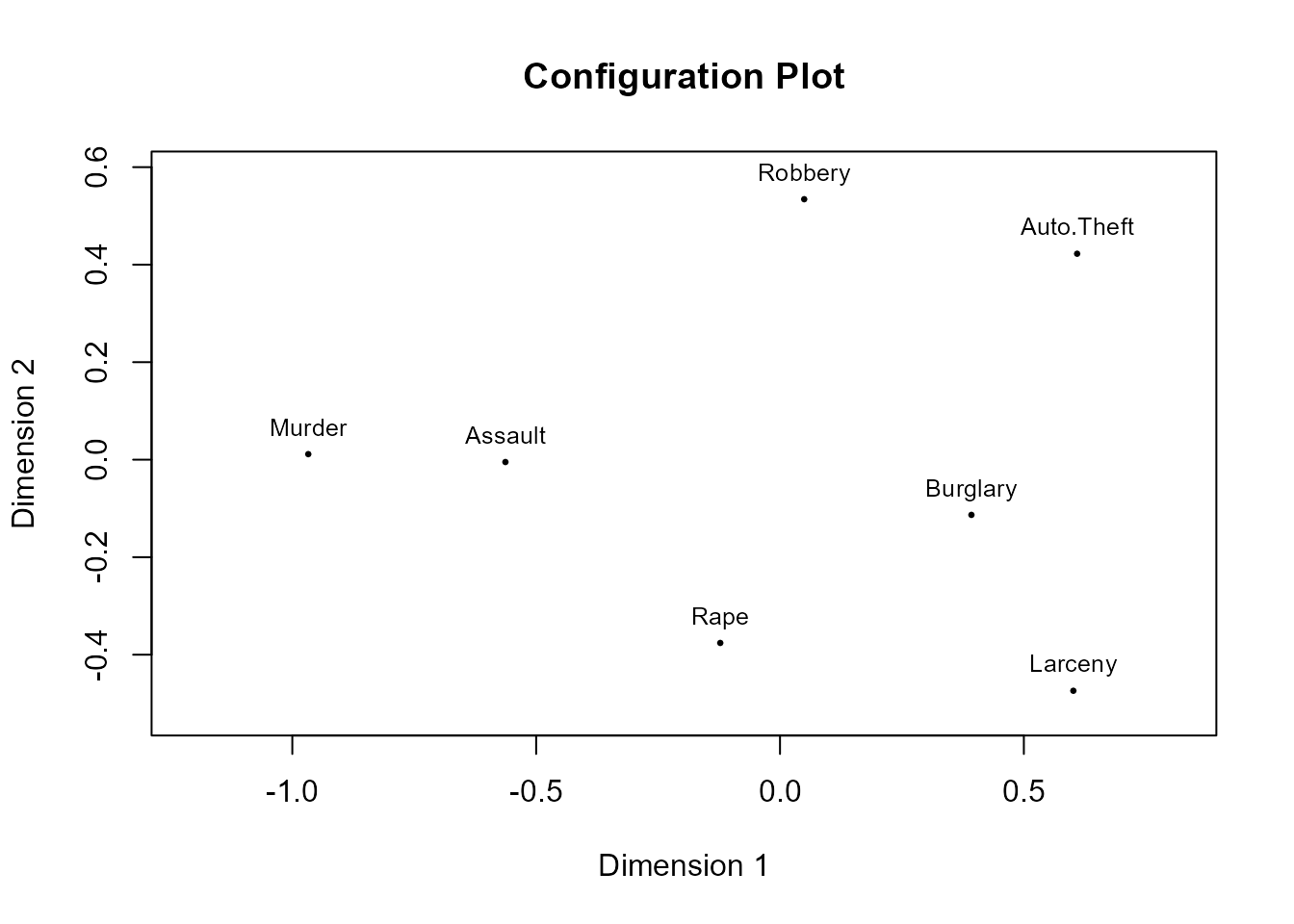

Figura 34.7: Representación bidimensional de las disimilitudes entre los siete tipos de delito.

Por último, para “interpretar” el sentido de las dimensiones en las que se representan los objetos, se recurre a ver cuáles están en los extremos. En la parte izquierda de la dimensión 1 están los delitos de asesinato y asalto, mientras que en la parte derecha están los de hurto, sustracción de vehículos y allanamiento; se podría decir, entonces, que es una dimensión relacionada con el grado de “personalización” del delito: los que afectan a personas directamente frente a los que no. La dimensión 2, con menos distancias (véanse las escalas) y de más difícil interpretación, contrapone en la parte superior los delitos con más “beneficio” económico (robos, sustracción de vehículos) frente a los que producen menos beneficio (parte inferior: violación o hurto); se podría decir, entonces, que es una dimensión asociada a la repercusión económica del delito.

Por último, cabe destacar que puede ser interesante analizar la estabilidad de las soluciones del EMD (bien mediante jackknife, bootstrap, o elipses de pseudoconfianza). También puede interesar plantear un modelo de EMD que permita valorar las diferencias individuales (abordable con la función smacofIndDiff()). Otra alternativa puede ser abordar un despliegue multidimensional, que representa conjuntamente objetos e individuos.

Resumen

La aplicación del EMD implica los siguientes tres pasos:

• La determinación de las proximidades originales entre los objetos. Esta fase depende de las características de los objetos y del tipo de relación que se quiera/pueda establecer entre ellos. Actualmente, R dispone de paquetes que permiten estimar las matrices de proximidad a partir de los datos en bruto.

• La conversión de las proximidades en similaridades (si fuese necesario) y el ajuste entre las originales y las reproducidas por el EMD. Se debe elegir el tipo de EMD a utilizar, que depende de la función de ajuste: se puede optar por funciones de tipo ratio, interval o mspline (EMD métricos) o ordinal (EMD no métrico). La elección estará relacionada con el tipo de datos usados y el grado de ajuste (Stress) de los modelos.

• La interpretación de los resultados a partir de la configuración obtenida, tanto del significado de las dimensiones como de la estructura de los objetos (cuáles se parecen, si existen grupos, etc.).