Capítulo 36 Redes neuronales artificiales

Noelia Vállez Enano\(^{a}\) y José Luis Espinosa Aranda\(^{a,b}\)

\(^{a}\)Universidad de Castilla-La Mancha
\(^{b}\)Ubotica Technologies

36.1 ¿Qué es el deep learning?

La inteligencia artificial (IA) es una disciplina científica que se ocupa de crear programas informáticos que ejecutan operaciones comparables a las que realiza la mente humana, como el aprendizaje o el razonamiento lógico (RAE, 2023). Entre otros ejemplos, se pueden encontrar en la actualidad tanto robots que son capaces de realizar tareas de manera similar a un humano en una fábrica como las denominadas casas inteligentes o los vehículos autónomos.

Dentro de las técnicas utilizadas para la IA se encuentran las técnicas clásicas de machine learning (véase Parte VI de este manual), las cuales tienen la habilidad de aprender sin haber sido explícitamente programadas para una tarea en particular, pudiendo ser utilizadas para varios fines y aplicaciones.

A su vez, dentro de las técnicas de machine learning, se enmarcan, como un subconjunto de ellas, las técnicas de deep learning, las cuales intentan simular tanto la arquitectura como el comportamiento del sistema nervioso humano –en particular, de las redes de neuronas que componen el encéfalo y que se encargan de realizar tareas específicas (véase la Fig. 36.1)–. Para ello, estas técnicas se basan en el concepto de redes neuronales, que intentan emular la forma de aprendizaje de los humanos (Goodfellow et al., 2016).

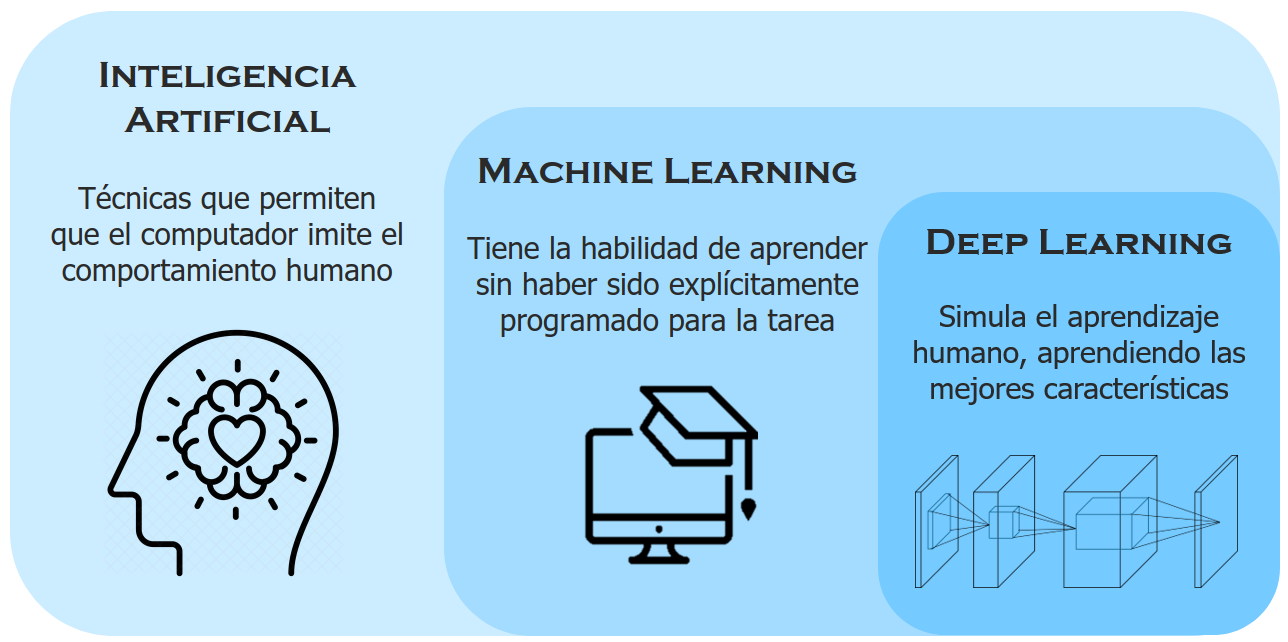
Figura 36.1: Inteligencia artificial, \(machine\) \(learning\) y \(deep\) \(learning\).

36.1.1 Diferencias entre las técnicas de machine learning tradicional y el deep learning

Como se vio en el Cap. 2, los métodos de ciencia de datos tienen una etapa llamada preparación de datos que incluye la tarea de selección de variables (véase Cap. 9) para determinar las mejores características o variables predictoras/clasificadoras en el marco del problema a resolver, características que, a su vez, deben ser entendidas por el algoritmo de machine learning seleccionado, de tal forma que este sea capaz de solucionar el problema planteado (véase Fig. 36.1).

Por ejemplo, en el caso de querer detectar una cara dentro de una imagen, sería necesario definir qué tipo de características servirían para detectar la misma, como podrían ser, a bajo nivel, determinados tipos de bordes de la imagen (véase la Fig. 36.2). Estas características proporcionarían la base para detectar a nivel medio elementos de la cara como ojos, narices, orejas, etc. y, definitivamente, a alto nivel, reconocer dónde hay una cara dentro de la imagen.

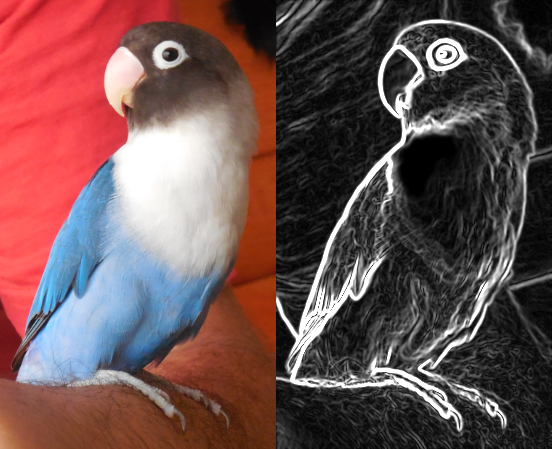
Figura 36.2: Detección de bordes de una imagen mediante el método de Scharr.

En muchas ocasiones, la selección de características requiere la intervención humana, por lo que puede llevar mucho tiempo y diversos experimentos de prueba y error hasta poder encontrar una combinación de características que permita resolver el problema planteado. Pues bien, las técnicas de deep learning, a diferencia de las de machine learning tradicional, son capaces de aprender cuáles son las características que permiten representar mejor el problema que se quiere resolver sin necesidad de la interacción humana a la vez que buscan la solución al mismo.

Continuando con el ejemplo anterior de la detección de caras, mientras que en las técnicas de machine learning es necesario indicar al algoritmo cuáles son las características base que componen una cara para que sea capaz de reconocerla, en las técnicas de deep learning únicamente es necesario mostrarle suficientes imágenes de caras para conseguir que el algoritmo sea capaz de aprender a identificar una cara por sí mismo, estableciendo de forma automática las características más importantes de una cara.

Esta capacidad de aprender por sí mismo las características determinantes a la hora de resolver un problema hace que, a nivel teórico, las técnicas de deep learning puedan llegar a ser más potentes que las del machine learning clásico. Sin embargo, dado que las técnicas de deep learning enfrentan problemas más complejos y, por consiguiente, procesos de entrenamiento más complicados, necesitan muchos más datos y una mayor potencia de cálculo para entrenar sus algoritmos.

Este hecho explica que, aunque las bases de las técnicas de deep learning como el algoritmo del descenso del gradiente (Kiefer & Wolfowitz, 1952), el perceptrón (Rosenblatt, 1958), los algoritmos de retropropagación y el perceptrón multicapa (Rumelhart et al., 1986) y la primera red neuronal convolucional (LeCun & Bengio, 1995) datan de varios años atrás, no sea hasta hace relativamente poco tiempo cuando se han podido empezar a utilizar. Esto se debe a diversos factores:

1. La evolución en el hardware de procesamiento. En particular, debido a la mejora de la capacidad de paralelismo masivo durante el cómputo que proporcionaron las nuevas tarjetas gráficas (GPU), al incorporar una gran cantidad de microprocesadores específicos, han podido ser utilizadas para las técnicas de deep learning. Originalmente su principal uso era representar modelos complejos 3D en los monitores, pero su utilización para técnicas de deep learning ha llevado recientemente al desarrollo de tarjetas específicas para este fin. Además, es posible disponer bajo demanda de estos recursos de computación como servicios a través de Internet. Esto es lo que se conoce como cloud computing.

2. El big data. La gran cantidad de datos que se generan y almacenan en la actualidad, así como la mayor facilidad a la hora de trabajar con esos conjuntos de datos (gracias a las nuevas herramientas disponibles), han permitido cubrir la necesidad del gran volumen de datos iniciales necesarios en estas técnicas.

3. La evolución del software. Recientemente ha habido un amplio interés tanto en buscar nuevos modelos para resolver todo tipo de problemas como en mejorar las técnicas utilizadas para entrenar redes neuronales. Esto ha llevado a la creación y mejora de diversos frameworks, librerías y aplicaciones relacionadas con el entrenamiento y despliegue de redes neuronales. Entre ellos destacan Keras, Tensorflow, Pytorch, Caffe2, Matlab y OpenVINO.

36.2 Aplicaciones del deep learning

Las posibles aplicaciones de las técnicas de deep learning son muy diversas y, gracias a la continua investigación desarrollada en el área en la actualidad, no hacen más que aumentar. A continuación se comentan algunas de ellas:

1. Clasificación de imágenes. Aunque la clasificación de imágenes dentro del área de la visión por computador, o artificial, es una realidad hace muchos años, es con las técnicas de deep learning con las que se han logrado los mayores avances (en particular, utilizando las redes neuronales convolucionales). Estas redes permiten determinar a qué clase, perteneciente al conjunto de categorías utilizado para entrenar, corresponde una determinada imagen.

2. Detección de objetos. Permite localizar los objetos contenidos en una imagen mediante un rectángulo, clasificándolo a su vez por su tipología. Por ejemplo, con este tipo de modelos es posible localizar y diferenciar entre peatones y vehículos utilizando una cámara de seguridad instalada en una calle (Fig. 36.3).

Figura 36.3: Detección de peatones y vehículos utilizando una cámara térmica y técnicas de \(deep\) \(learning\).

3. Segmentación semántica/de instancias. De forma similar a la detección de objetos, la segmentación semántica permite localizar objetos contenidos en una imagen, además de su tipología, pero en este caso se marcan utilizando una máscara a nivel de píxel. La segmentación de instancias además es capaz de diferenciar entre diferentes instancias de una misma clase aun cuando se encuentren situadas de forma contigua.

4. Reconocimiento del habla. Permite a un computador procesar y comprender el habla humana. Ya existen varios asistentes inteligentes basados en esta tecnología que, además, son capaces de interpretar órdenes o instrucciones sencillas y actuar en consecuencia.

5. Traducción automática. Consiste en utilizar las técnicas de deep learning para traducir un texto automáticamente de una lengua a otra sin la necesidad de intervención humana. En la actualidad, no se limita únicamente a la traducción literal, palabra por palabra, del texto, sino que también tiene en cuenta el significado que tendría en el idioma original para adaptarlo al idioma destino (Fig. 36.4).

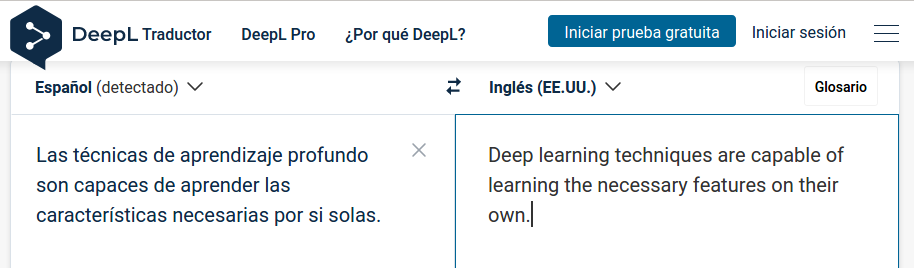
Figura 36.4: Traductor automático basado en \(deep\) \(learning\).

6. Generación automática de imágenes/texto. Permite obtener, desde una imagen, un texto descriptivo que indique el contenido de la imagen; o al contrario, a partir de un texto descriptivo generar una imagen basada en dicha descripción. Un ejemplo de este último caso sería Dall-E (Borji, 2022), que puede verse en la Fig. 36.5.

Figura 36.5: Algunas salidas posibles del generador de imágenes a partir de texto Dall-E, para el texto: \(A\) \(cat\) \(with\) \(glasses\) \(studying\) \(computer\) \(vision\) \(in\) \(the\) \(space\) \(with\) \(the\) \(Earth\) \(in\) \(the\) \(background\).

7. Automóvil autónomo. Las técnicas de deep learning están siendo claves para el desarrollo del vehículo autónomo, capaz de circular sin necesidad de la interacción de un conductor humano. Para lograr definitivamente un vehículo con estas características, es necesario que sea capaz de ver, tomar decisiones y conducir al mismo tiempo. Esto se consigue en la actualidad integrando la información de gran cantidad de sensores que obtienen datos en tiempo real sobre el entorno –como serían cámaras, LIDAR, radares o ultrasónicos, entre otros– que es procesada por varias redes neuronales con el fin de que el sistema de conducción sea capaz de tomar una decisión en cuestión de milisegundos (Fig. 36.3).

8. Chatbots con IA. Son aplicaciones software que, utilizando la IA conversacional, son capaces de conversar mediante un chat escrito como si fueran un ser humano. Cabe destacar los asistentes virtuales existentes en diversas páginas web y el reciente ChatGPT (OpenAI, 2022), el cual es capaz de mantener conversaciones con el usuario, resolver problemas sencillos, generar textos y resúmenes sobre cualquier tema o generar código en diversos lenguajes de programación a partir de una petición realizada mediante lenguaje natural.

36.3 Redes neuronales

Las redes neuronales artificiales (en inglés artificial neural networks, ANN) tienen su origen en la definición de neurona artificial de McCulloch & Pitts (1943) y en el diseño del perceptrón por parte de Frank Rosenblatt (Rosenblatt, 1958). Cada ANN está formada por un conjunto de elementos conocidos como ``neuronas” cuya organización está inspirada en la que siguen las redes neuronales de los seres vivos. Entre dos neuronas adyacentes existe una serie de conexiones a través de las cuales se envía la información como si de pulsos eléctricos se tratase. De forma aislada, cada neurona procesa la información recibida para producir un resultado que será utilizado por las siguientes neuronas con las que está conectada.

Cada ANN tiene como objetivo resolver una tarea concreta. Por ejemplo, una ANN podría estar diseñada para reconocer un dígito o una letra a partir de una imagen. Para resolver dicha tarea, la red sigue un proceso de aprendizaje automático. Este proceso se conoce como ``entrenamiento” y requiere que se disponga de un conjunto de datos representativos de la tarea a resolver.

36.4 Perceptrón o neurona

El elemento básico de toda ANN es la neurona artificial, inspirada en las neuronas biológicas. Cada neurona tiene una serie de entradas y produce una única salida. Las entradas pueden ser valores de las variables seleccionadas para resolver el problema en estudio o salidas de otras neuronas de la red.

Para calcular la salida, primeramente, cada neurona realiza una suma ponderada de sus entradas utilizando una serie de pesos, \(\bf w\), donde \(w_i\in \mathbb{R}\), y añade un término constante, \(w_0\in \mathbb{R}\):

\[\begin{equation} \bf w^{\prime} \bf x = w_0 + w_1 x_1 + w_2 x_2 + \dots + w_n x_n . \end{equation}\]

Una vez obtenida la suma ponderada, normalmente se pueden separar las entradas en dos conjuntos, obteniéndose como salida final un valor binario, siguiendo la fórmula:

\[\begin{equation} f (\bf w^{\prime} \bf x) = \begin{cases} 1 & \text{si $\bf w^{\prime} \bf x>0$}\\ 0 & \text{en otro caso.} \end{cases} \end{equation}\]

Por tanto, cada neurona actúa como un clasificador lineal que puede separar dos conjuntos diferentes dependiendo de si la salida es positiva o negativa (Fig. 36.6).

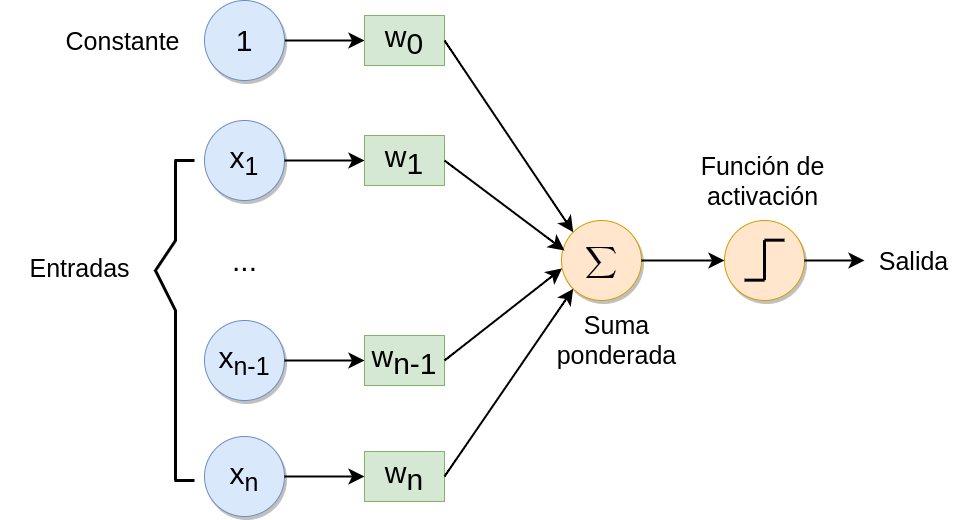
Figura 36.6: Estructura del perceptrón o neurona.

36.4.1 Aprendizaje

Durante el proceso de aprendizaje, el perceptrón busca el ajuste automático de los valores de los pesos. Estos deben seleccionarse de forma que minimicen el error de clasificación (predicción en su caso) cometido sobre un conjunto de entrenamiento. El conjunto de entrenamiento, \(D\), está compuesto por un conjunto de \(h\) observaciones de las que se conoce su clase:

\[\begin{equation} D = \{ ({\bf x}_1 , y_1 ), ({\bf x}_2 , y_2 ), \dots, ({\bf x}_h , y_h ) \}, \end{equation}\]

donde cada \({\bf x}_i = (x_{1i},x_{2i},\dots,x_{pi})\), pertenece a una de las dos clases, \(y_i = {0,1 }, \hspace{0,5cm} i=1,2,...h\).

El primer paso del aprendizaje o entrenamiento consiste en la inicialización de cada peso \(w_j, \hspace{0,1cm} j=1,2,...,p,\) a 0 o a algún otro valor aleatorio.

Tras ello, se calcula la clase asignada a cada \(\hat y_i\) en un momento determinado, \(t\), para cada colección de valores \(\boldsymbol x_i\) del conjunto de datos de entrenamiento: \[\begin{equation} \hat y_i(t) = f({\bf w}(t)^{\prime} {\bf x}_i) = f(w_0(t) + w_1(t) \cdot x_{1i} + \dots + w_p(t) \cdot x_{pi}). \end{equation}\]

Tras obtener la salida para todas las observaciones del conjunto de entrenamiento, cada uno de los pesos de la neurona, \(w_j\), se actualiza siguiendo la fórmula: \[\begin{equation} w_j(t+1) = w_j(t) + \lambda |y_i-\hat y_i(t)|\cdot x_{ji}. \end{equation}\]

donde \(|y_i-\hat y_i(t)|\) es 0 cuando la clase predicha coincide con la clase real de la observación y \(\lambda\) es la tasa de aprendizaje. La tasa de aprendizaje debe seleccionarse de antemano y controla la variación de los pesos entre iteraciones. En algunos casos el valor de \(\lambda\) es 0 o varía durante el proceso de entrenamiento.

Los dos pasos anteriores se repiten hasta que el error de clasificación sea menor que un cierto umbral, \(u\) o el número de iteraciones alcance un cierto valor fijado. Normalmente se suele utilizar el número de iteraciones como criterio de parada puesto que no siempre es posible alcanzar una tasa de error más baja que la deseada.

36.4.2 Convergencia

El teorema de la convergencia del perceptrón establece que, en los problemas en los que haya dos clases linealmente separables, es siempre posible encontrar unos pesos que realicen la separación en un número finito de iteraciones (Novikoff, 1962). Sin embargo, la mayoría de los problemas que se estudian no son linealmente separables, esto es, no es posible obtener un conjunto de variables que separen perfectamente, de forma lineal, las observaciones de cada clase. Por ello, en estos casos, es necesario el uso de ciertas estrategias que solucionen el problema de convergencia. Algunas de las estrategias más utilizadas son:

• Algoritmo Pocket: guarda la mejor solución obtenida hasta el final del entrenamiento.

• Algoritmo Maxover: halla el margen de separación máximo permitiendo clasificaciones incorrectas.

• Algoritmo de Voto: se utilizan múltiples perceptrones combinando sus salidas.

36.5 Perceptrón multiclase

Una extensión lógica del uso del perceptrón es su empleo en la resolución de tareas de clasificación donde existan más de dos clases (Haykin, 1999). En ese caso se tendrá un conjunto de entrenamiento, \(D\), de \(m\) muestras:

\[\begin{equation} D = { ({\bf x}_1 , y_1 ), ({\bf x}_2 , y_2 ), \dots, ({\bf x}_h , y_h ) }, \end{equation}\]

donde cada muestra \({\bf x}_i = (x_{1i},x_{2i},\dots,x_{pi})\) pertenece a una de las \(k\) clases posibles:

\[\begin{equation} y_i = \{ 0,1,\dots,k-1 \} . \end{equation}\]

A diferencia del problema binario, en la versión multiclase del perceptrón multiclase lo que se definen son varios modelos, \(F\), uno para cada una de las \(k\) clases:

\[\begin{equation} F=\{f_0,f_1,\dots,f_{k-1}\}\\ , \hspace{0,1cm}f_m \{m=0,1,...,k-1\}: \mathbb{R}^p \rightarrow \mathbb{R}. \end{equation}\]

En este caso la salida no se selecciona en función de si el valor obtenido es positivo o negativo, sino que se asigna la clase del modelo que obtenga el valor más alto tras aplicar los pesos a la muestra. Esta estrategia recibe el nombre de ``uno contra todos”:

\[\begin{equation} \hat y_i = argmax_{m}\hspace{0,1cm}f_m(\boldsymbol x_i)\\ ,\hspace{0,2cm}m\in\{0,1,\dots ,k-1\} . \end{equation}\]

En muchas ocasiones lo que se obtiene no es un único valor con la clase asignada como salida, sino que se obtiene un vector con las salidas binarias de cada uno de los modelos empleados. En ese caso, el vector contendrá un 1 en la posición de la clase asignada y un 0 en el resto de clases. Por ejemplo, el vector \([0,1,0,0,0]\) representaría que una muestra ha sido asignada a la segunda clase en un problema de clasificación donde existen 5 clases posibles:

\[\begin{equation} [f_0({\bf x}_i),f_1({\bf x}_i)),\dots,f_{k-1}({\bf x} _i)] . \end{equation}\]

36.6 Funciones de activación

Además de los pesos, toda neurona tiene asociada una función de activación. Esta función se encarga de transformar la suma ponderada de las entradas en el resultado final. En las secciones anteriores se ha utilizado una función de activación con umbral 0, pero existen muchas otras. Algunas de las más utilizadas se enumeran a continuación.

Para algunas de ellas, se ha implementado una función, plot_activation_function(), que permite dibujarlas en R:

library("ggplot2")
library("latex2exp")
plot_activation_function <- function(f, title, range){
  ggplot(data.frame(x=range), mapping=aes(x=x)) +
    geom_hline(yintercept=0, color='black', alpha=3/4) +
    geom_vline(xintercept=0, color='black', alpha=3/4) +
    stat_function(fun=f, colour = "red") +
    ggtitle(title) +
    scale_x_continuous(parse(text = TeX(r'(w$\prime$x)'))) +
    scale_y_continuous(parse(text = TeX(r'(f(w$\prime$x))'))) +
    theme(plot.title = element_text(hjust = 0.5))
}

• Función lineal. Se trata de una función identidad donde la salida tiene el mismo valor que la entrada. Normalmente se aplica en problemas de regresión lineal, por ejemplo, si se quiere predecir el número de días que lloverá en un mes determinado. Su expresión es:

\[\begin{equation} f({\bf w}^{\prime} \bf x)={\bf w}^{\prime} \bf x, \end{equation}\]

y su representación gráfica es de la siguiente forma (Fig 36.7):

f <- function(x){ x }
plot_activation_function(f, 'Lineal', c(-4,4))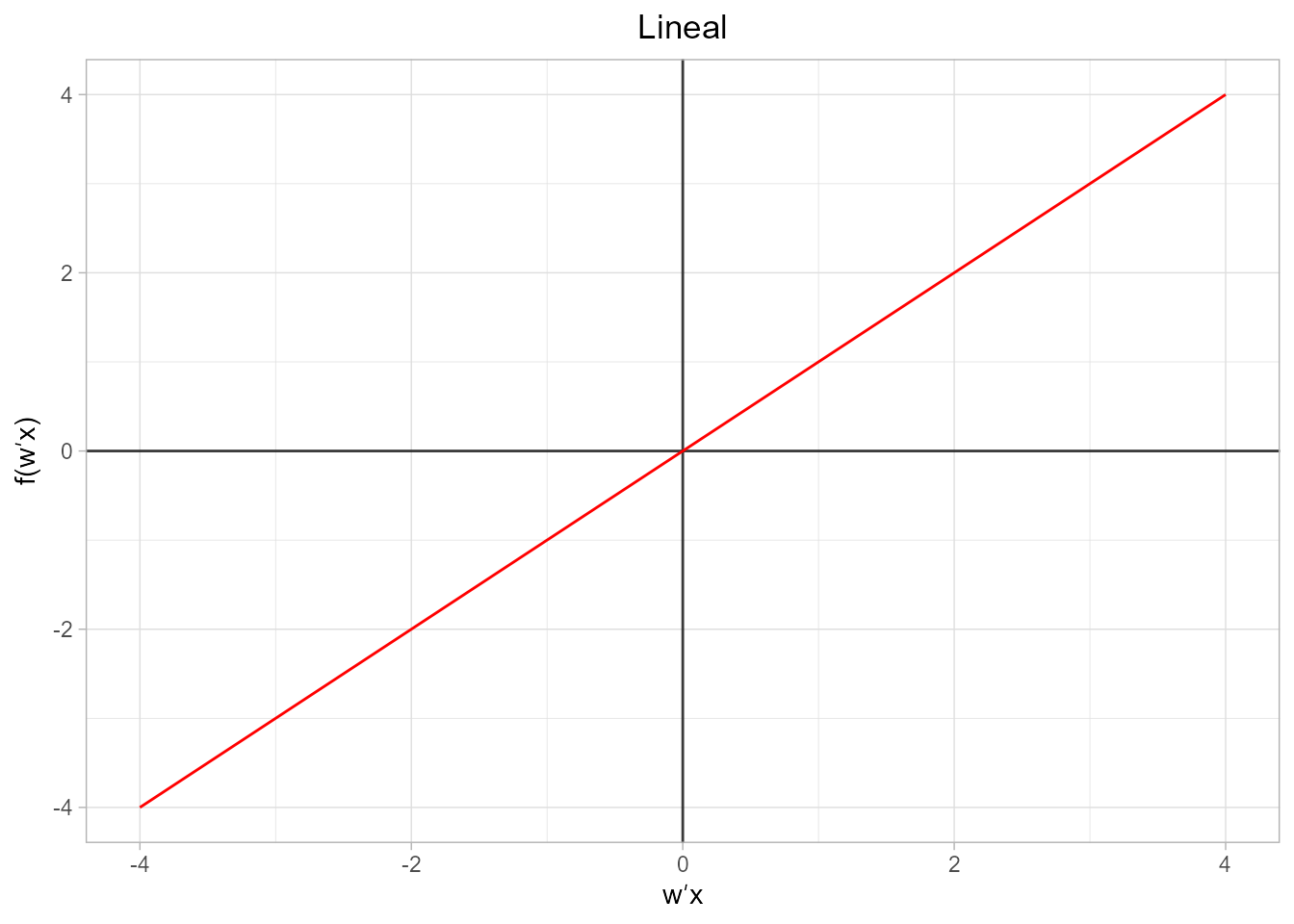

Figura 36.7: Representación gráfica de la función lineal.

• Función umbral. Esta función recibe también el nombre de función escalón. Si el valor de entrada es menor que el umbral, \(u\), la salida es 0. En caso contrario, la salida es 1. Si el umbral es 0, la función se reduce a observar el signo del valor de la salida.

\[\begin{equation} f({\bf w}^{\prime} {\bf x})=\begin{cases} 0 & \text{si ${\bf w}^{\prime} {\bf x}<u$}\\ 1 & \text{en otro caso}. \end{cases} \end{equation}\]

Se representa gráficamente mediante el código que aparece a continuación, el cual se corresponde con una modificación de la función plot_activation_function(), ya que la versión original no mostraría de forma correcta la gráfica al requerir representar dos valores en la posición 0: el valor 0 y el valor 1 del escalón (Fig. 36.8):

df <- data.frame(x=c(-4, -3, -2, -1, 0, 1, 2, 3, 4), f=c(0,0,0,0,1,1,1,1,1))
ggplot(data=df, aes(x=x, y=f, group=1)) +
    theme(plot.title = element_text(hjust = 0.5)) +
    ggtitle("Umbral")+
    scale_y_continuous(parse(text = TeX(r'(f(w$\prime$x))'))) +
    scale_x_continuous(parse(text = TeX(r'(w$\prime$x)'))) +
    geom_hline(yintercept=0, color='black', alpha=3/4) +
    geom_vline(xintercept=0, color='black', alpha=3/4) +
    geom_step(color='red')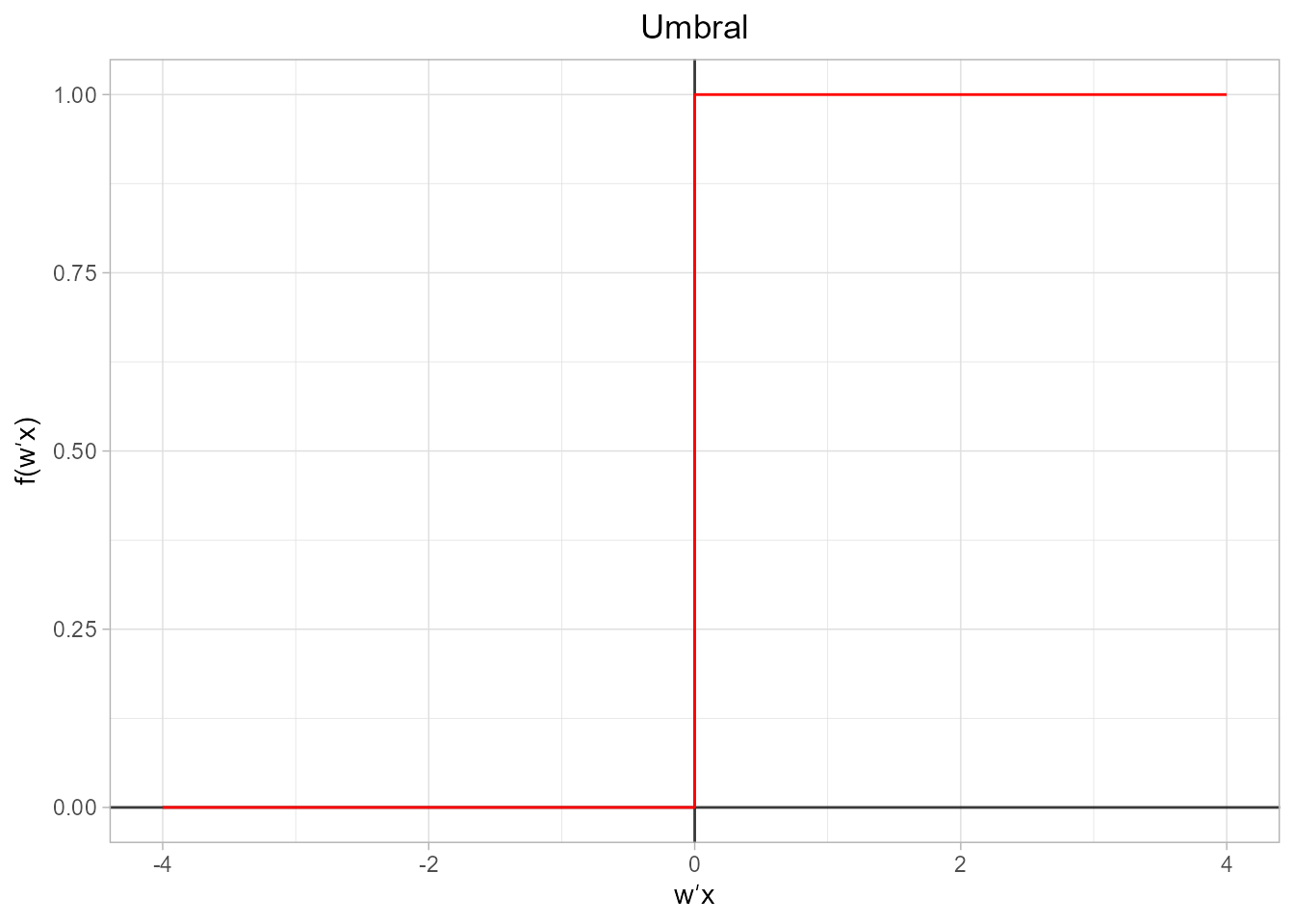

Figura 36.8: Representación gráfica de la función umbral.

• Función sigmoide. También conocida como función logística, se trata de una de las funciones más utilizadas para asignar una clase. Si el punto de evaluación de la función es un valor negativo muy bajo, la función da como resultado un valor muy cercano a 0, si se evalúa en 0 el resultado es 0,5 y si se evalúa en un valor positivo alto el resultado es aproximadamente 1.

\[\begin{equation} f( {\bf w}^{\prime} {\bf x})=\frac{1} {1-e^{-{\bf w}^{\prime} {\bf x}}}. \end{equation}\]

   Su representación gráfica es como sigue (Fig. 36.9):

f <- function(x){1 / (1 + exp(-x))}
plot_activation_function(f, 'Sigmoide', c(-4,4))

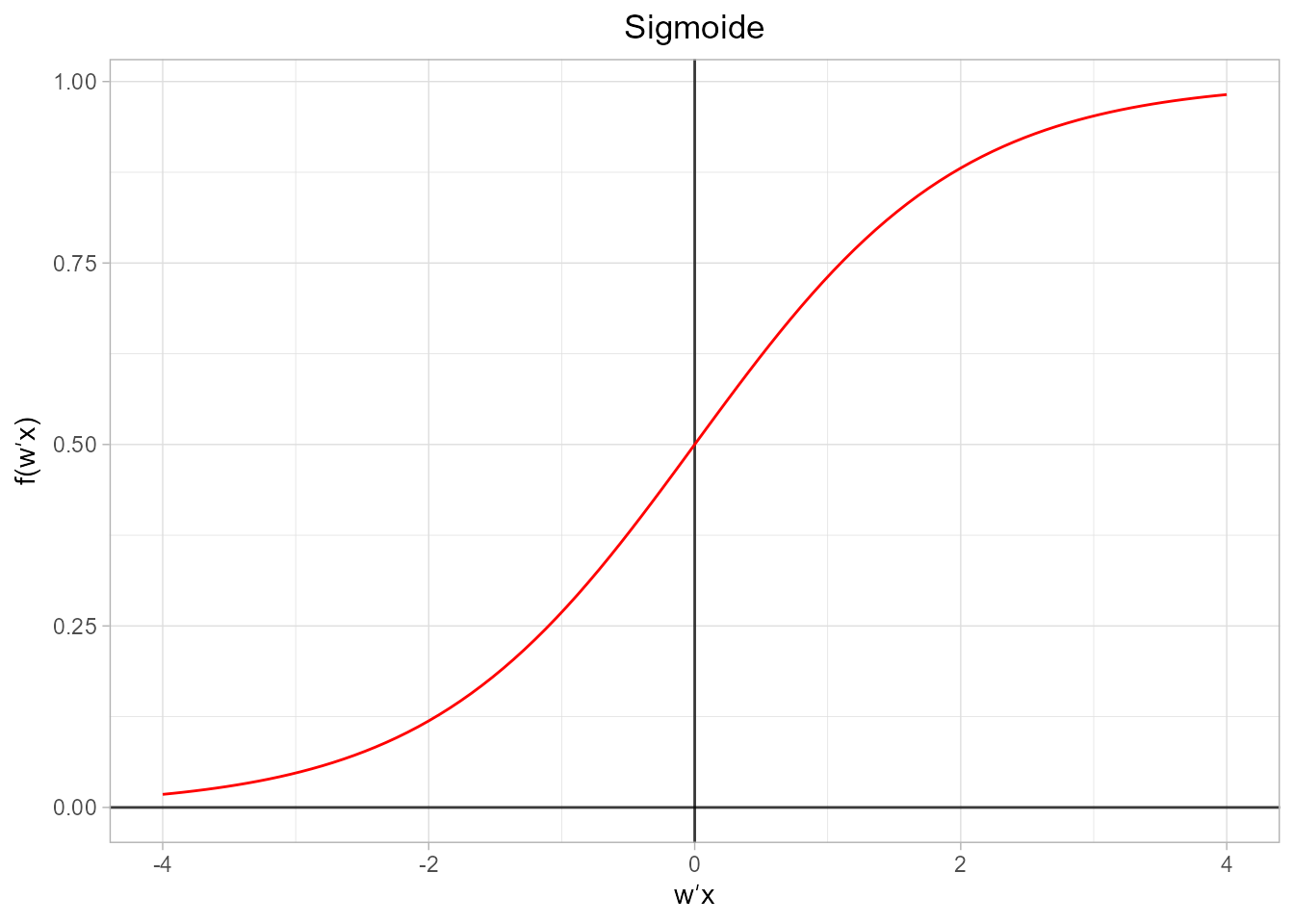
Figura 36.9: Representación gráfica de la función sigmoide.

• Función tangente hiperbólica. El rango de valores de salida es [-1, 1], donde para valores altos de \({\bf w}^{\prime} \bf x\) la función tiende de manera asintótica a 1 y los valores muy bajos tiende, también de manera asintótica, a \(-1\), de forma similar a la sigmoide.

\[\begin{equation} f({\bf w}^{\prime} \bf x)=\frac{e^{{\bf w}^{\prime} {\bf x}} -e^{-{\bf w}^{\prime} \bf x}} {e^{{\bf w}^{\prime} \bf x}+e^{-{\bf w}^{\prime} \bf x}}. \end{equation}\]

   Su representación gráfica es como sigue (Fig. 36.10):

tanh_func <- function(x){tanh(x)}
plot_activation_function(tanh_func, 'Tangente Hiperbólica', c(-4,4))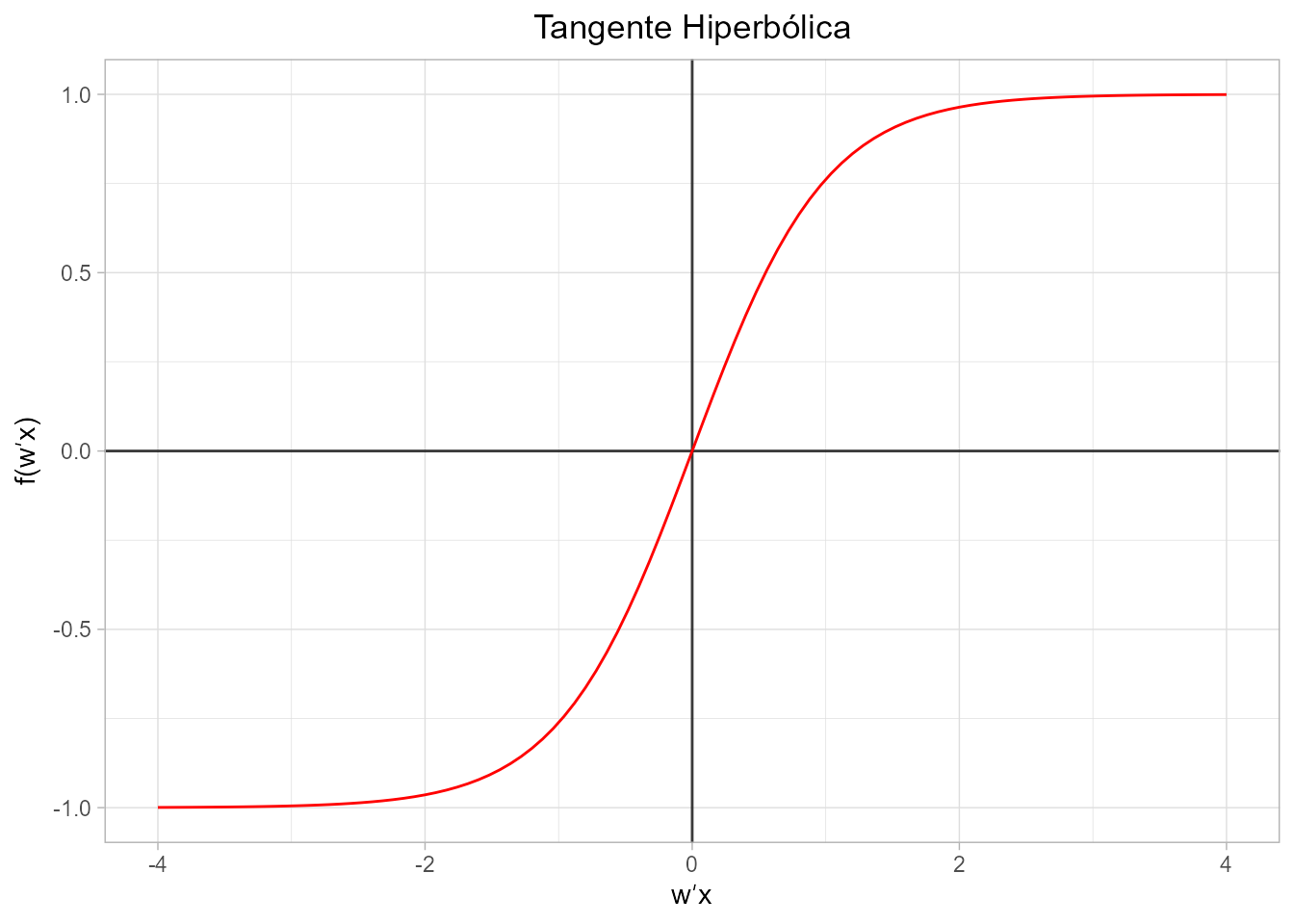

Figura 36.10: Representación gráfica de la función tangente hiperbólica.

• Función ReLU. Se trata de la unidad lineal rectificada (del inglés rectified linear unit). Es posiblemente la función de activación más utilizada actualmente en deep learning (Nair & Hinton, 2010).

\[\begin{equation} f({\bf w}^{\prime} {\bf x})=\begin{cases} 0 & \text{si ${\bf w}^{\prime} {\bf x}\leq 0$}\\ {\bf w}^{\prime} {\bf x} & \text{en otro caso}, \end{cases} \end{equation}\]

   y se representa gráficamente de la siguiente manera (Fig. 36.11):

rec_lu_func <- function(x){ ifelse(x < 0 , 0, x )}
plot_activation_function(rec_lu_func, 'ReLU', c(-4,4))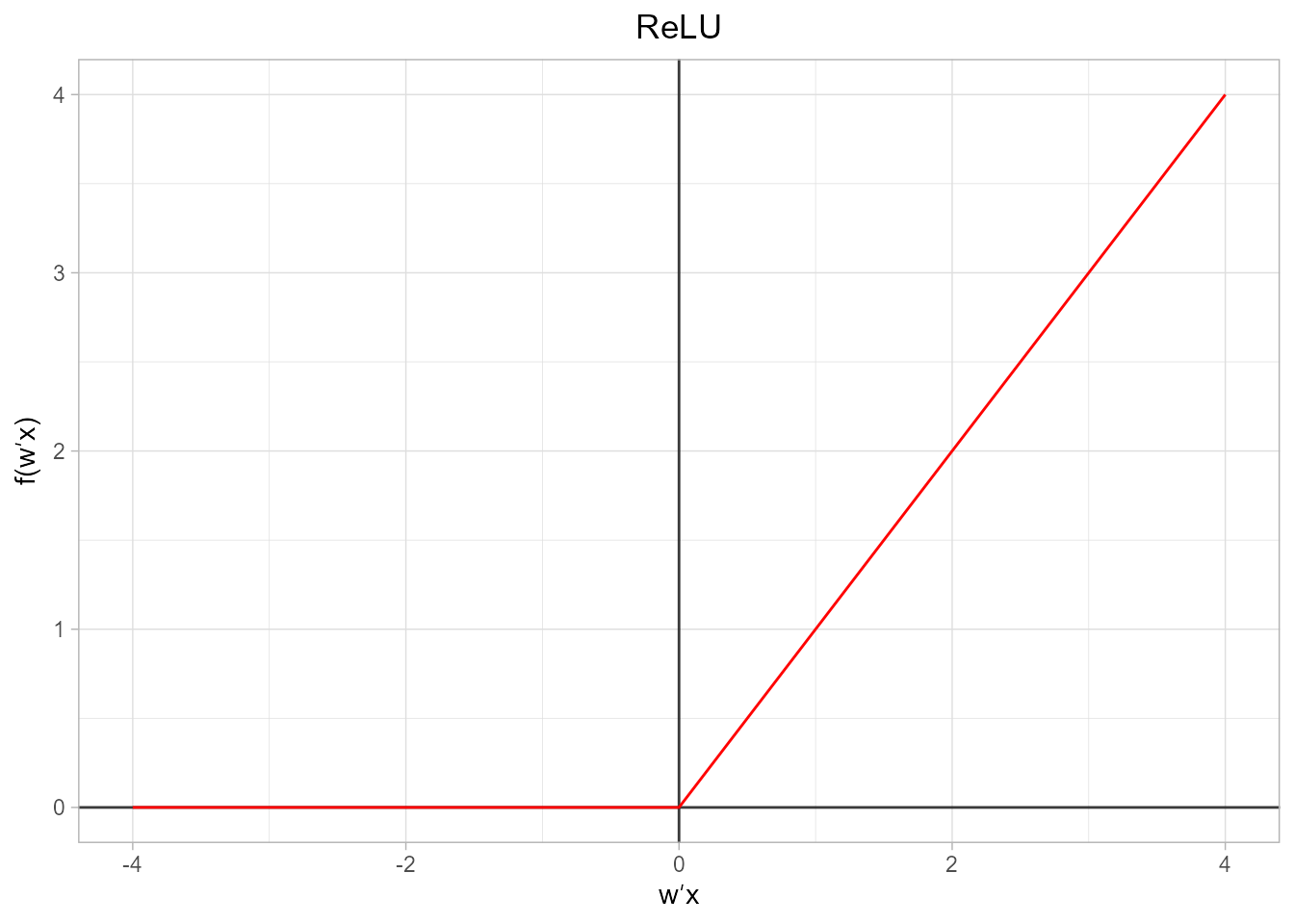

Figura 36.11: Representación gráfica de la función ReLU.

36.7 Perceptrón multicapa

Aunque el perceptrón puede aprender muchos tipos de lógica, no es posible que aprenda la operación XOR (OR exclusivo), que se diferencia del OR en que asigna un 1 a la salida cuando las dos entradas son distintas (Minsky & Papert, 1969). El perceptrón multicapa o, en inglés, multilayer perceptron (MLP) surge para dar una solución a este problema, que es un paradigma de los problemas linealmente no separables, que realmente son la mayoría en el mundo real.

Un MLP está compuesto por varias capas con neuronas. La primera capa es la de entrada, que recibe las variables seleccionadas para dar solución al problema a resolver. La última, la salida del MLP, representa las clases de salida (en las que hay que clasificar las entradas). Entre ambas capas hay una o más capas intermedias u “ocultas”. Las neuronas de una capa intermedia tienen como entrada la salida de la capa anterior y su salida es la entrada de las neuronas de la siguiente capa (Fig. 36.12). Este tipo de capas también son llamadas densas o totalmente conectadas. En la práctica, tanto las capas intermedias como la capa de salida están compuestas por neuronas totalmente conectadas.

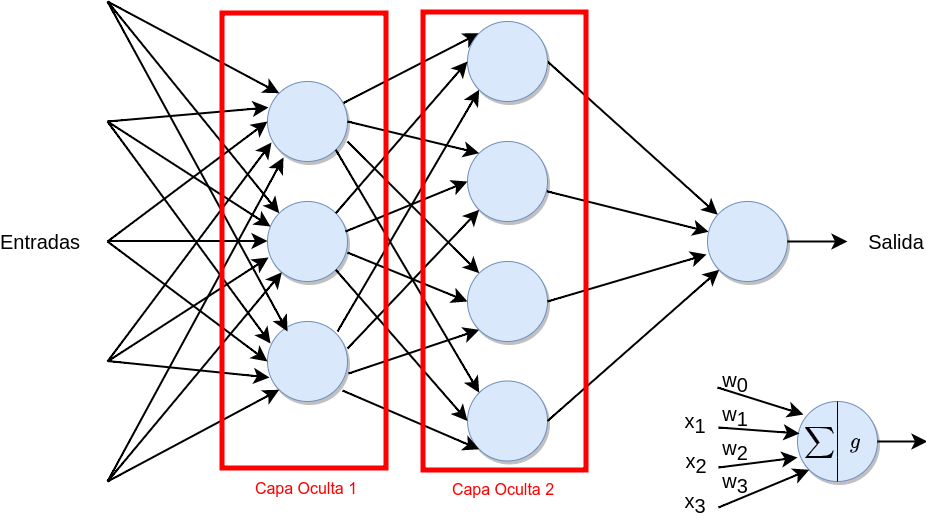
Figura 36.12: Estructura del perceptrón multicapa (MLP).

36.7.1 Aprendizaje

El MLP entra en la categoría de los algoritmos de propagación hacia adelante, o feedforward, ya que las entradas de las neuronas de una capa, que se combinan mediante su suma ponderada, pasan por una función de activación y el resultado es propagado a las neuronas de la capa siguiente. Este proceso se lleva a cabo desde la capa de entrada hasta la capa de salida.

Dado un conjunto de observaciones de entrenamiento:

\[\begin{equation} D = \{ ({\bf x}_1 , y_1 ), ({\bf x}_2 , y_2 ), \dots, ({\bf x}_h , y_h ) \}, \end{equation}\]

donde cada \(\boldsymbol x_i \in \mathbb{R}^p\) (siendo \(p\) el número de características) e \(y_i \in \{0, 1\}\).

El vector \({\bf z}_1\) cuyos elementos son las sumas ponderadas de las \(c_1\) neuronas de la primera capa intermedia, \({\bf z}_j, \hspace{0,1cm} j=1, 2,..c_1\), para una entrada genérica \({\bf x}\), viene dado por la expresión:

\[\begin{equation} {\bf z}_1 = {\bf W}_{(1)}^{\prime} {\bf x} + {\bf b}_1 , \end{equation}\]

donde \({\bf b}_{1} \in \mathbb{R}^{p}\) es un vector con las constantes de la primera capa, siendo \(p\) el número de variables de cada capa, y \({\bf{W}}_{(1)} \in \mathbb{R}^{c_1 \times p}\) la matriz de pesos de la capa.

Tras aplicar la función de activación, \(g(\cdot)\), al vector de sumas ponderadas de las neuronas de la primera capa intermedia, \({\bf z}_1\in \mathbb{R}^{c_1}\), se obtiene el vector de salidas de dichas neuronas:

\[\begin{equation} {\bf h}_{1}= g({\bf z}_1). \end{equation}\]

Como las salidas de las neuronas de una capa intermedia son las entradas de las neuronas de la siguiente capa, en la siguiente capa el vector que contiene las salidas de sus neuronas es:

\[\begin{equation} {\bf h}_{2} = g ( {\bf W}_{(2)}^{\prime} {\bf h_1)} + {\bf b}_2). \end{equation}\]

En general, el vector de salidas de las neuronas de la \(c\)-ésima capa intermedia (\(c=1,2,...,C\)) se obtiene como:

\[\begin{equation} {\bf h}_{c} = g ( {\bf W}_{(c)}^{\prime} {\bf h}_{c-1}) + {\bf b}_c). \end{equation}\]

Siguiendo el mismo razonamiento, en una red con \(C\) capas densas o totalmente conectadas (\(C-1\) capas ocultas o intermedias y una capa de salida), la salida de la red, \(\hat y\), para una entrada \(\bf x\), viene dada por:

\[\begin{equation} \hat y = g ( {\bf W}_{(C)}^{\prime} {\bf h}_{C-1} + {\bf b}_C ), \end{equation}\]

siendo \(C\) el número de capas (\(C-1\) intermedias y una de salida).

Por ejemplo, en una red con tres capas densas, dos intermedias y una de salida, la salida es:

\[\begin{equation} \hat y = g \left( {\bf W}_{(3)}^{\prime} g \left( {\bf W}_{(2)}^{\prime} g \left( {\bf W}_{(1)}^{\prime} {\bf x} + {\bf b}_1 \right) + {\bf b}_2 \right)+ {\bf b}_3 \right) . \end{equation}\]

Para entrenar y ajustar los pesos de este tipo de redes es necesario realizar el ajuste de la combinación de todos los pesos de la red. De forma similar a la búsqueda de los pesos óptimos en el caso de una sola neurona (véase Sec. 36.4.1), será necesario encontrar la combinación de valores que clasifiquen bien todas las muestras del conjunto de entrenamiento o, en su defecto, que fallen en el menor número de muestras posible o minimicen alguna otra función de coste. En este punto es donde entra en juego la propagación hacia atrás o backpropagation.

La propagación hacia atrás es el mecanismo por el que el MLP ajusta de forma iterativa los pesos de la red con el objetivo de minimizar una función de coste que mide lo bueno o malo que es el resultado obtenido en un momento determinado (Rumelhart et al., 1986). Su único requisito de aplicación es que todas las operaciones de la red (incluidas las funciones de activación) sean diferenciables ya que se utiliza el algoritmo del descenso del gradiente para optimizar la función de coste.

El MLP utiliza diferentes funciones de coste o pérdida según el tipo de problema a resolver. Para los problemas de clasificación, la función de coste más utilizada es la entropía cruzada media (en inglés average cross-entropy, ACE). Para un problema binario esta función de coste se calcula como:

\[\begin{equation} C(\hat{y},y,{\bf W}) = -\dfrac{1}{h}\sum_{i=0}^n(y_i \ln {\hat{y_i}} + (1-y_i) \ln{(1-\hat{y_i})}) + \dfrac{\alpha}{2h} ||{\bf W}||_2^2 , \end{equation}\]

donde \(h\) es el número de observaciones contenidas en el conjunto de entrenamiento, \(\bf{W}\) es la matriz que contiene los pesos de la red, \(\alpha ||W||_2^2\) (con \(\alpha > 0\)) es un término de regularización, L2, también conocido como penalización ya que penaliza los modelos complejos. \(\alpha\) es un hiperparámetro cuyo valor se establece manualmente.

Para los problemas de regresión, la función de coste se basa en el error cuadrático medio (mean squared error, MSE):

\[\begin{equation} C(\hat{y},y,\boldsymbol W) = \frac{1}{2n}\sum_{i=0}^n||\hat{y}_i - y_i ||_2^2 + \frac{\alpha}{2n} ||\boldsymbol W||_2^2 . \end{equation}\]

Cada iteración en el proceso de aprendizaje estará compuesta entonces por dos etapas: una de propagación hacia adelante y otra de propagación hacia atrás. En la primera etapa se introducen los valores de entrada a la red y se propagan las operaciones y los resultados hasta obtener la salida final de la red. En la segunda, el gradiente de la función de coste es propagado hacia atrás para actualizar los valores de los pesos de todas las capas y acercarse más a los valores que minimizan la función de coste.

En el algoritmo del descenso del gradiente, \(\nabla C_{\boldsymbol W}\) (la derivada multivariante de la función de coste respecto a todos los parámetros de la red) se calcula y deduce de \(\boldsymbol W\).

Formalmente esto puede expresarse como:

\[\begin{equation} \boldsymbol W^{t+1} = \boldsymbol W^{t} - \lambda \nabla {C}_{\boldsymbol W}^{t} , \end{equation}\]

donde \(t\) es el estado de la red en una iteración determinada y \(\lambda\) es la tasa de aprendizaje, cuyo valor debe ser superior a 0.

Al igual que en el caso del perceptrón único, el entrenamiento terminará cuando se alcance un número máximo de iteraciones o la mejora en la función de coste entre dos iteraciones consecutivas no supere cierto umbral.

Durante el proceso de aprendizaje, es necesario guardar en la memoria los resultados de cada una de las muestras del conjunto de entrenamiento. Si el número de muestras o el tamaño de la red son grandes, es posible que no se disponga del espacio suficiente. Para resolver este problema, en una iteración no se utiliza todo el conjunto de entrenamiento, sino que se emplea un subconjunto del mismo llamado batch. El conjunto de entrenamiento se divide en cada iteración, por tanto, en un número de batches disjuntos con un número de observaciones por batch. Atendiendo a esta división, es posible definir una serie de hiperparámetros:

• Tamaño del batch. Número de observaciones utilizadas en cada iteración para actualizar los pesos.
• Número de épocas. Número de pasadas completas sobre el conjunto de entrenamiento hasta terminar el proceso de aprendizaje.
• Número de iteraciones por época. Es el resultado de dividir el número total de observaciones por el tamaño del batch.

Por ejemplo, si se tiene un conjunto de 55.000 observaciones y el tamaño del batch es de 100, cada época tendrá 550 iteraciones.

36.8 Instalación de librerías de deep learning en R: Tensorflow/Keras

El framework que se utiliza en este libro para trabajar con técnicas de deep learning es Tensorflow/Keras, debido a que \((i)\) es uno de los más completos en la actualidad, \((ii)\) permite realizar una configuración completa del proceso de entrenamiento y \((iii)\) permite trabajar con diversos tipos de redes neuronales.

Para poder utilizar Tensorflow/Keras en R, es necesario realizar la instalación de la librería fuera de R. Por ello, si ya se dispone de una instalación de la misma sería posible utilizarla. No obstante, se recomienda seguir los pasos indicados a continuación para tener una instalación nativa de Tensorflow/Keras asociada directamente a R.

• Paso 1: instalación de la librería de tensorflow en R.

install.packages("tensorflow")

A continuación, será necesario tener una instalación de Conda en el sistema. Los usuarios tanto de Windows como de Linux/Mac pueden realizar directamente la instalación de una versión de Conda denominada Mini-Conda en el instalador del siguiente paso, opción recomendada para no tener que realizar una instalación externa de manera adicional.

Nota

Otra opción para los usuarios de Windows, pero no recomendada por los autores de este libro salvo que ya se tenga instalado Anaconda, es utilizar el programa y la librería directamente dentro de Anaconda, instalando una versión de R directamente en el sistema a través del siguiente link:

https://docs.anaconda.com/anaconda/install/windows/

• Paso 2: instalación de tensorflow y keras.

Para continuar la instalación hay que activar la librería tensorflow y ejecutar la función install_tensorflow():

library("tensorflow")
install_tensorflow()

Al ejecutar esta función, los usuarios deben marcar “Y” para aceptar la instalación de Mini-Conda, descartando aceptar la utilización de cualquier otro sistema Conda que pueda estar instalado previamente.

También se puede ejecutar la función install_keras() del paquete keras para instalar Tensorflow.

install.packages("keras")
library("keras")
install_keras()

• Paso 3: confirmar la instalación.

La instalación se puede comprobar con los siguientes comandos (la salida puede variar según el equipo, pero la línea final tiene que ser similar a la indicada):

library("tensorflow")
tf$constant("Hellow Tensorflow")

tf.Tensor(b'Hellow Tensorflow', shape=(), dtype=string)

36.9 Ejemplo de red para clasificación en R

En esta sección se entrena una red neuronal artificial para reconocer o clasificar los dígitos manuscritos del conjunto de datos MNIST (https://en.wikipedia.org/wiki/MNIST_database). Cada una de las imágenes de este conjunto de datos tiene un tamaño de \(28\times28\) píxeles²⁴⁶ en escala de grises. En vez de extraer una serie de variables a partir de cada imagen, en este caso se utilizan cada uno de los \(28\times28=784\) píxeles como variable de entrada (véase Fig. 36.13).

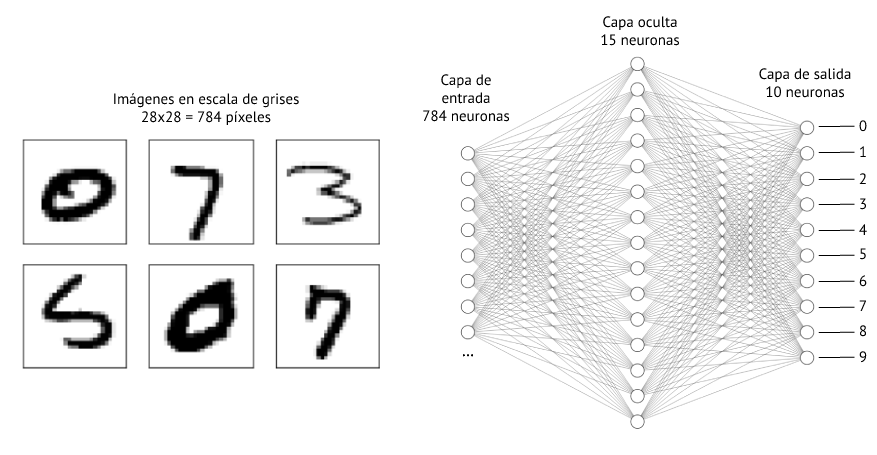
Figura 36.13: MLP para reconocimiento de dígitos manuscritos.

36.9.1 Carga y visualización de los datos

El primer paso consiste en cargar la librería keras, que permite crear redes neuronales y descargar el conjunto de imágenes que se encuentra disponible públicamente:

library("keras")
mnist <- dataset_mnist()

A continuación, se puede ver el contenido de las variables generadas, que en este caso contienen los valores de los píxeles de las imágenes. Cabe destacar que el conjunto de datos MNIST ya viene separado en dos subconjuntos, uno para entrenamiento y otro para test, compuestos por 60.000 y 10.000 imágenes, respectivamente. En ambos casos, estos datos se almacenan en la variable de nombre x.

names(mnist)
#> [1] "train" "test"
dim(mnist$train$x)
#> [1] 60000    28    28
dim(mnist$train$y)
#> [1] 60000
dim(mnist$test$x)
#> [1] 10000    28    28
dim(mnist$test$y)
#> [1] 10000

Además, las imágenes de cada subconjunto vienen acompañadas de la clase a la que pertenecen (dígito contenido en la imagen). En ambos casos, esta etiqueta se almacena en la variable con nombre y. A continuación se muestra un pequeño ejemplo que permitirá visualizar alguna de las imágenes contenidas en el conjunto de datos de entrenamiento junto con la etiqueta que indica el dígito contenido (Fig. 36.14):

par(mfcol=c(4, 4))
par(mar=c(0, 0, 3, 0), xaxs='i', yaxs='i')
for (j in 1:16) {
    im <- mnist$train$x[j, , ]
    im <- t(apply(im, 2, rev))
    image(x=1:28, y=1:28, z=im, col=gray((0:255)/255),
          xaxt='n', main=paste(mnist$train$y[j]))
}

Figura 36.14: Algunas imágenes del conjunto de entrenamiento.

36.9.2 Preprocesamiento

Una vez cargados los datos y comprobado su contenido se puede llevar a cabo algún tipo de preprocesado. Dependiendo del tipo de problema, se podrán realizar unas operaciones u otras. Por ejemplo, cuando se trabaja con imágenes es muy típico estandarizar los valores de color de las imágenes para mitigar las diferencias producidas por las diferentes condiciones de iluminación.

En este caso, solo se van a transformar los valores originales de los píxeles de cada imagen (en rango de 0 a 255, véase nota a pie de página 1) a valores entre 0 y 1 dividiendo cada valor por el máximo, 255:

mnist$train$x <- mnist$train$x/255
mnist$test$x <- mnist$test$x/255

36.9.3 Generación de la red neuronal

El siguiente paso consiste en la generación de la red neuronal. Para ello, se define primero la estructura, utilizando la interfaz sequential proporcionada por Tensorflow/Keras a través de la función keras_model_sequential():

model <- keras_model_sequential() |>
  layer_flatten(input_shape = c(28, 28)) |>
  layer_dense(units = 15, activation = "relu") |>
  layer_dense(10, activation = "softmax")

Como se puede observar, la red definida está compuesta por una capa de tipo flatten²⁴⁷ que se encarga de transformar los \(28 \times 28\) valores en un vector de 784 elementos, para que a continuación una capa oculta dense²⁴⁸ de 15 neuronas con activación relu se encargue de realizar las primeras operaciones con esos datos. Al final, una última capa dense se encarga de obtener la probabilidad de que la imagen represente cada una de las posibles clases mediante una activación softmax:²⁴⁹

summary(model, line_length=64)

#> Model: "sequential"
#> ____________________________________________________________________
#>  Layer (type)              Output Shape               Param #    
#> ====================================================================
#>  flatten (Flatten)         (None, 784)                0          
#>  dense_1 (Dense)           (None, 15)                 11775      
#>  dense (Dense)             (None, 10)                 160        
#> ====================================================================
#> Total params: 11,935
#> Trainable params: 11,935
#> Non-trainable params: 0
#> ____________________________________________________________________

Finalmente, es necesario compilar el modelo, indicando algunos de los parámetros de configuración necesarios para el proceso de entrenamiento, como la función de coste o pérdida, el optimizador a utilizar y las métricas a obtener:

model |>
  compile(
    loss = "sparse_categorical_crossentropy", # función utilizada para problemas de clasificación con varias clases
    optimizer = "sgd", # stochastic gradient descent
    metrics = "accuracy" # Precisión
  )

36.9.4 Entrenamiento

Una vez generada la estructura de la red neuronal y definida la anterior configuración, es posible entrenarla mediante la función fit(). Para ello, se le debe indicar el conjunto de imágenes de entrenamiento, x, que debe utilizar y sus clases correspondientes, y. Además de otros parámetros, se podrá configurar el número de épocas a entrenar (epochs, pasadas sobre el conjunto completo de entrenamiento), el tamaño del batch que se utilizará en cada iteración (batch_size, número de imágenes por iteración), qué porcentaje de elementos del conjunto de datos se utilizan para validar el modelo (validation_split, imágenes utilizadas durante el entrenamiento pero solo para obtener una estimación real del error cometido) y la tasa de aprendizaje (learning_rate).

training_evolution <- model |>
  fit(
    x = mnist$train$x, y = mnist$train$y,
    epochs = 10, batch_size = 128,
    validation_split = 0.2,
    learning_rate = 0.1,
    verbose = 2
  )

#> Epoch 1/10
#> 375/375 - 2s - loss: 1.6313 - accuracy: 0.5266 - val_loss: 1.0455 - val_accuracy: 0.7510 - 2s/epoch - 6ms/step
#> Epoch 2/10
#> 375/375 - 1s - loss: 0.8433 - accuracy: 0.7881 - val_loss: 0.6409 - val_accuracy: 0.8434 - 1s/epoch - 3ms/step
#> Epoch 3/10
#> 375/375 - 1s - loss: 0.6022 - accuracy: 0.8427 - val_loss: 0.5031 - val_accuracy: 0.8712 - 1s/epoch - 3ms/step
#> Epoch 4/10
#> 375/375 - 1s - loss: 0.5047 - accuracy: 0.8656 - val_loss: 0.4381 - val_accuracy: 0.8830 - 1s/epoch - 3ms/step
#> Epoch 5/10
#> 375/375 - 1s - loss: 0.4526 - accuracy: 0.8767 - val_loss: 0.4019 - val_accuracy: 0.8909 - 1s/epoch - 3ms/step
#> Epoch 6/10
#> 375/375 - 1s - loss: 0.4201 - accuracy: 0.8854 - val_loss: 0.3764 - val_accuracy: 0.8959 - 1s/epoch - 3ms/step
#> Epoch 7/10
#> 375/375 - 1s - loss: 0.3976 - accuracy: 0.8896 - val_loss: 0.3593 - val_accuracy: 0.8996 - 1s/epoch - 3ms/step
#> Epoch 8/10
#> 375/375 - 1s - loss: 0.3809 - accuracy: 0.8939 - val_loss: 0.3463 - val_accuracy: 0.9022 - 1s/epoch - 3ms/step
#> Epoch 9/10
#> 375/375 - 1s - loss: 0.3678 - accuracy: 0.8975 - val_loss: 0.3359 - val_accuracy: 0.9050 - 1s/epoch - 3ms/step
#> Epoch 10/10
#> 375/375 - 1s - loss: 0.3571 - accuracy: 0.8997 - val_loss: 0.3289 - val_accuracy: 0.9064 - 1s/epoch - 3ms/step

Las gráficas de coste/pérdida y precisión permiten ver su evolución durante el proceso de entrenamiento (Fig. 36.15):

plot(training_evolution)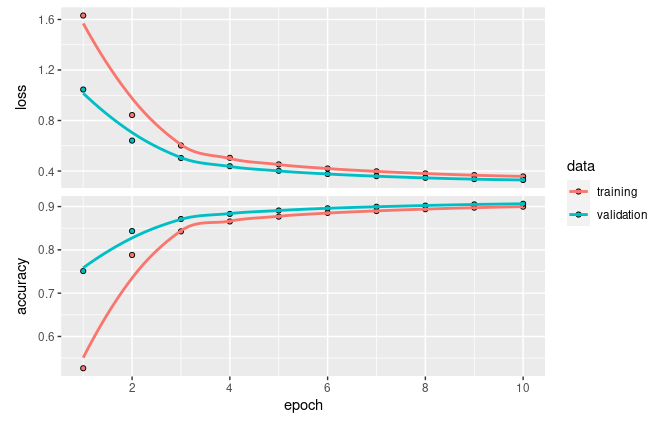

Figura 36.15: Evolución durante el entrenamiento de la función de precisión y de coste/pérdida: conjuntos de entrenamiento y validación.

Como se puede observar, la red entrenada tiene alrededor de un 90% de precisión (porcentaje de aciertos al clasificar las imágenes) tanto para las imágenes del conjunto de entrenamiento como para las del conjunto de validación. En el caso de la función de pérdida o coste, que mide el error cometido al realizar la clasificación, se aprecia que se reduce conforme la precisión del modelo aumenta.

36.9.5 Test

Una vez entrenado el modelo, es posible aplicarlo sobre el conjunto de test. Para ello, se puede realizar la predicción sobre cualquiera de las imágenes mediante la función predict, obteniendo la probabilidad de que pertenezca a una determinada clase:

predictions <- predict(model, mnist$test$x)
head(round(predictions, digits=3), 5)
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#> [1,] 0.000 0.000 0.000 0.003 0.000 0.000 0.000 0.995 0.000 0.002
#> [2,] 0.009 0.000 0.836 0.024 0.000 0.009 0.119 0.000 0.003 0.000
#> [3,] 0.000 0.962 0.013 0.006 0.001 0.001 0.003 0.002 0.010 0.002
#> [4,] 0.999 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
#> [5,] 0.001 0.000 0.007 0.000 0.836 0.004 0.011 0.012 0.017 0.111

También se puede utilizar la función evaluate() para calcular tanto el coste o pérdida como la precisión de la red neuronal sobre el conjunto de test. Como se puede observar, se obtienen valores muy similares a los conseguidos durante el entrenamiento:

model |>
  evaluate(mnist$test$x, mnist$test$y, verbose = 0)
#> loss      accuracy
#> 0.3310305 0.9045000

Con la función predict() se puede también generar la matriz de confusión de la red para evaluar aciertos y fallos para cada clase:

prediction_matrix <- model |> predict(mnist$test$x) |> k_argmax()
confusion_matrix <- table(as.array(prediction_matrix), mnist$test$y)
confusion_matrix

#>    
#>        0    1    2    3    4    5    6    7    8    9
#>   0  953    0   11    4    2   16   16    3    8    7
#>   1    0 1108   10    2    6    1    3   21   10    5
#>   2    4    3  901   27    5   11   14   27   13    6
#>   3    2    2   16  903    0   46    1    4   29   10
#>   4    1    0   16    0  899   16   12    9   11   43
#>   5    6    1    1   29    1  726    8    1   24   13
#>   6    9    4   19    3   10   21  902    0   10    0
#>   7    2    2   12   17    2   10    0  916   11   18
#>   8    3   15   35   20   10   38    2    3  839    9
#>   9    0    0   11    5   47    7    0   44   19  898

La diagonal principal contiene el número de aciertos del modelo entrenado para el conjunto de test, mientras que el resto de valores indican en cuántas ocasiones una clase es clasificada de manera incorrecta como otra diferente. A partir de esta matriz de confusión se puede calcular el valor de accuracy mediante la función evaluate().

36.9.6 Guardado y reutilización del modelo

Finalmente, es posible almacenar el modelo entrenado mediante la función save_model_tf, que genera una carpeta con la red que se puede cargar y reutilizar mediante la función load_model_tf.

save_model_tf(object = model, filepath = "model")
reloaded_model <- load_model_tf("model")
round(predict(reloaded_model, mnist$test$x[1,1:28,1:28]), digits=4)
#>       [,1]   [,2]   [,3]   [,4]  [,5]  [,6]  [,7]    [,8]   [,9]    [,10]
#> [1,] 2e-04     0   1e-04 0.0028     0 1e-04     0  0.9948      0    0.002

36.10 Ejemplo de red para regresión en R

En esta sección se entrena una red neuronal artificial para predecir el precio de la vivienda en Madrid en función de sus características. Para ello se usa el conjunto de datos Madrid_Sale disponibles en el paquete de R Idealista18, que contiene información del año 2018 y que fue utilizado en el Cap. 9. Se toman como variables predictoras (capa de entrada) las siguientes:

• CONSTRUCTEDAREA: metros cuadrados construidos.
• ROOMNUMBER: número de habitaciones.
• BATHNUMBER: número de baños.
• HASLIFT: si tiene o no ascensor.
• DISTANCE_TO_CITY_CENTER: distancia al centro de la ciudad.
• DISTANCE_TO_METRO: distancia a la estación de metro más cercana.
• DISTANCE_TO_CASTELLANA: distancia a La Castellana.

36.10.1 Carga y visualización de los datos

Considerando que ya se ha cargado previamente la librería keras, se carga el conjunto de datos indicando las variables a considerar:

library("idealista18")
data("Madrid_Sale")

variables <- c("CONSTRUCTEDAREA","ROOMNUMBER","BATHNUMBER",
               "HASLIFT","DISTANCE_TO_CITY_CENTER","DISTANCE_TO_METRO",
               "DISTANCE_TO_CASTELLANA")
x_madrid <- Madrid_Sale[variables]
x_madrid_mat <- unname(data.matrix(x_madrid))
y_madrid <- Madrid_Sale$PRICE
y_madrid_mat <- matrix(y_madrid,nrow = length(y_madrid),byrow = TRUE)

El conjunto de datos contiene un total de 94.815 elementos. El 90% ellos se destinará al conjunto de entrenamiento y el 10% restante al de validación o test:

ind <- sample(c(TRUE, FALSE), length(y_madrid), replace=TRUE, prob=c(0.9, 0.1))
madrid_dat_train_x <- x_madrid_mat[ind, ]
madrid_dat_test_x <- x_madrid_mat[!ind, ]
madrid_dat_train_y <- y_madrid_mat[ind, ]
madrid_dat_test_y <- y_madrid_mat[!ind, ]

36.10.2 Preprocesamiento

Una vez cargados los datos y comprobado su contenido, se recomienda normalizar las variables seleccionadas como predictoras, puesto que normalmente son muy heterogéneas. Aunque la red neuronal podría adaptarse a una situación de heterogeneidad, dicha adaptación podría complicar el proceso de entrenamiento, lo cual se traduciría en mayor imprecisión. Para llevar a cabo el proceso de normalización se utiliza la función scale() sobre las variables predictoras; adicionalmente, se divide la variable precio entre 100.000 para reducir su escala:

madrid_dat_train_x <- scale(madrid_dat_train_x)
madrid_dat_test_x <- scale(madrid_dat_test_x)
madrid_dat_train_y <- madrid_dat_train_y/100000
madrid_dat_test_y <- madrid_dat_test_y/100000

36.10.3 Generación de la red neuronal

El siguiente paso consiste en la generación de la red neuronal. Para ello, igual que en la sección 36.9.3, primero se define su estructura utilizando la interfaz sequential proporcionada por Tensorflow/Keras a través de la función keras_model_sequential():

model <- keras_model_sequential() |>
  layer_dense(units=128, activation="relu", input_shape=7) |>
  layer_dense(units=64, activation="relu") |>
  layer_dense(units=16, activation="relu") |>
  layer_dense(units=1)

Como se puede observar, la red está compuesta por varias capas tipo dense (además de la de entrada) en las que las tres primeras tienen una activación relu. La última capa dense se encarga de proporcionar el valor de la predicción y, al contrario que en el ejemplo previo, no incluye ningún tipo de función de activación, puesto que su valor ya es comprensible tanto para el modelo como para su interpretación. Esto sería equivalente a utilizar la función de activación lineal.

summary(model, line_length=64)

#> Model: "sequential_1"
#> ________________________________________________________________
#>  Layer (type)               Output Shape              Param #   
#> ================================================================
#>  dense_5 (Dense)            (None, 128)               1024      
#>  dense_4 (Dense)            (None, 64)                8256      
#>  dense_3 (Dense)            (None, 16)                1040      
#>  dense_2 (Dense)            (None, 1)                 17        
#> ================================================================
#> Total params: 10,337
#> Trainable params: 10,337
#> Non-trainable params: 0
#> ________________________________________________________________

Finalmente, se compila el modelo indicando los parámetros de configuración necesarios para el proceso de entrenamiento. En este caso la función de coste o pérdida es el error cuadrático medio y la métrica, el error absoluto medio:

model |>
  compile(
    loss = "mse", # mean squared error
    optimizer = "sgd", # stochastic gradient descent
    metrics = "mae" # mean absolute error
  )

36.10.4 Entrenamiento

Una vez generada la estructura de la red neuronal y definida la anterior configuración, se entrena la red con la función fit(), configurando el resto de parámetros de forma similar a como se vio en la sección 36.9.4:

training_evolution <- model |>
  fit(
    x = madrid_dat_train_x, y = madrid_dat_train_y,
    epochs = 50, batch_size = 512,
    validation_split = 0.2,
    learning_rate = 0.1,
    verbose = 2
  )

Las gráficas de coste/pérdida y error durante el proceso de entrenamiento pueden verse en la Fig. 36.16.

plot(training_evolution)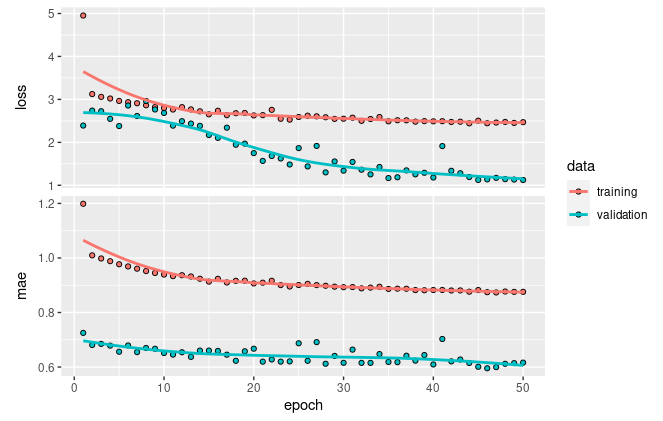

Figura 36.16: Evolución durante el entrenamiento de la precisión y la pérdida: conjuntos de entrenamiento y validación.

Como se puede observar, en este caso el modelo tiene aún posibilidad de mejora, ya que la pérdida es elevada y no se ha estancado, por lo que incrementando el número de épocas y el tiempo de entrenamiento se podría obtener un mejor resultado.

36.10.5 Test

Una vez entrenado el modelo, es posible aplicarlo sobre el conjunto de test mediante la función predict(), obteniendo la predicción del precio de cada una de las viviendas incluidas en dicho conjunto:

predictions <- predict(model, madrid_dat_test_x)
head(predictions, 5)
#> [,1]
#> [1,] 6.669374
#> [2,] 5.895504
#> [3,] 3.887646
#> [4,] 6.390513
#> [5,] 5.721725

Y mediante la función evaluate() se calcula tanto el coste o pérdida como el error de la red neuronal sobre el conjunto de test (véase Fig. 36.16), el cual se tiene que multiplicar por 100.000 para obtener el resultado en la escala original del conjunto de datos:

model |>
  evaluate(madrid_dat_test_x, madrid_dat_test_y, verbose = 0)
#> loss mae
#> 2.4195166 0.9227165

Resumen

• En este capítulo se ha explicado en detalle el concepto de redes neuronales artificiales, incluyendo los elementos que la componen, desde el perceptrón o neurona básica hasta el perceptrón multicapa, pasando el perceptrón multiclase, junto al proceso de aprendizaje de los mismos.

• Además, se han definido las funciones de activación clásicas utilizadas en las redes neuronales artificiales, las cuales se encargan de transformar la suma ponderada de las entradas en el resultado final de la capa.

• Finalmente, se han explicado los pasos necesarios para poder entrenar una red neuronal artificial utilizando la librería Tensorflow/Keras en R, resolviendo un problema de clasificación de dígitos manuscritos, a partir del conjunto de datos MNIST, y un problema de regresión para predecir el precio de la vivienda en Madrid en función de sus características, a partir del conjunto de datos de Idealista18.