Capítulo 37 Redes neuronales convolucionales

Noelia Vállez Enano\(^{a}\) y José Luis Espinosa Aranda\(^{a,b}\)

\(^{a}\)Universidad de Castilla-La Mancha
\(^{b}\)Ubotica Technologies

37.1 Introducción

Las redes neuronales convolucionales (en inglés convolutional neural network, CNN) son una extensión de las redes neuronales artificiales (ANN) en las que se incluyen capas convolucionales, explicadas en detalle en las siguientes secciones, para aprender a extraer, de forma automática, las características de los datos de entrenamiento al inicio de la arquitectura (Fig. 37.1).

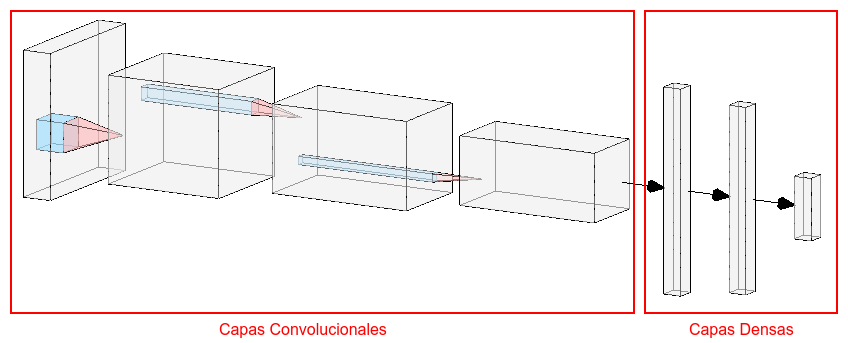
Figura 37.1: Estructura general de una CNN.

Las primeras capas convolucionales de la red aprenden a extraer características generales de los datos de entrada, mientras que las últimas capas convolucionales extraen características mucho más específicas. Cuanto más larga (o más profunda) es la red, mayor cantidad de detalles podrá aprender a distinguir. Esto es lo que ha propiciado la aparición del término ``aprendizaje profundo” (Goodfellow et al., 2016).

Tras las capas convolucionales suelen encontrarse las capas densas o totalmente conectadas de la misma tipología de las vistas en el Cap. 36. Esta parte de la red será la encargada de realizar la clasificación de las observaciones en función de los valores de las características extraídas en la parte convolucional. Por tanto, se dice que este tipo de redes tiene dos partes: una de extracción de características (realizada por la red convolucional) y otra de clasificación o regresión (como las vistas en el Cap. 36).

37.2 Convolución

Aunque las ANN pueden utilizarse con los valores de color de una imagen como variables para reconocer qué hay en ella (véase Cap. 36), no permiten extraer información de carácter espacial (de indudable importancia en el estudio de fenómenos con datos anclados al espacio y con dependencia espacial, entre otros ámbitos). Para lidiar con este problema, las CNN incorporan capas convolucionales para extraer características de las observaciones con las que se alimenta la red, incluyendo información sobre la estructura espacial (LeCun & Bengio, 1995).

Las convoluciones realizan una tarea similar al sistema visual humano; de hecho, se inspiran en cómo el ser humano percibe y procesa las características de los objetos. Aunque se diseñaron principalmente para ayudar a resolver tareas de visión por computador, donde la entrada de la red es una imagen, es posible utilizarlas también con entradas vectoriales o series temporales.

Una convolución aplica un filtro sobre la entrada siguiendo un proceso de ventana deslizante. El filtro (o kernel) no es otra cosa que una matriz con unos pesos que se centra en cada uno de los valores de la entrada para calcular una media ponderada de los valores de la entrada, siendo las ponderaciones los valores del filtro (Bueno et al., 2015). El tamaño de los filtros suele ser, por tanto, impar.

La Fig. 37.2 muestra el resultado de aplicar la operación de convolución con un filtro de tamaño \(3 \times 3\) sobre una matriz de entrada de tamaño \(5 \times 5\). El resultado será una matriz, \(\bf M\), de tamaño \(3 \times 3\), cuyos elementos se calculan como sigue: se pone el filtro sobre los valores de entrada de tal manera que quede centrado sobre el valor de interés de la entrada y se calcula la suma ponderada de los valores de las entradas sobre las que se sitúa el filtro, siendo las ponderaciones los valores del filtro.²⁵⁰

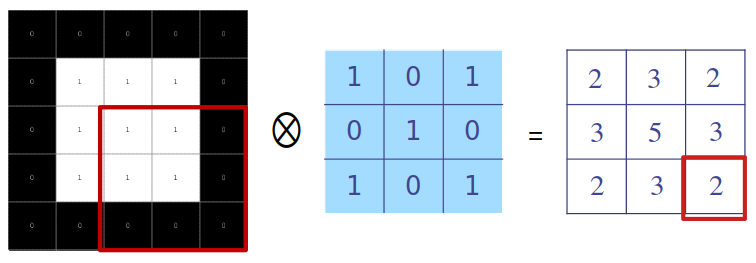
Figura 37.2: Ejemplo de convolución. De izquierda a derecha: entrada (negro = 0, blanco = 1), filtro y salida.

En general, una convolución en dos dimensiones se define como:

\[\begin{equation} {\bf M}[x,y]=\sum_{s=-a}^{a}\sum_{t=-b}^{b} {\bf F}[s,t] {\bf E}[x-s,y-t], \end{equation}\]

donde \(\bf F\) es el filtro a aplicar, \(\bf E\) es la matriz de entrada, \(\bf M\) es la matriz de resultado, que recibe también el nombre de ``mapa de características”, y \(a\) y \(b\) son los tamaños de los desplazamientos desde el centro del filtro a cualquier otro valor.

Por tanto, cada valor del ejemplo de la Fig. 37.2 se obtiene como:

\[\begin{gather} \begin{aligned} M_{1,1} = 1\cdot0+ 0\cdot 0+1 \cdot 0+0 \cdot 0 + & 1 \cdot 1 + 0 \cdot 1+ 1\cdot 0 +0\cdot 1 +1 \cdot 1=2 \\ M_{1,2} = 1\cdot0+ 0\cdot 0+1 \cdot 0+0 \cdot 1 + & 1 \cdot 1 + 0 \cdot 1+ 1\cdot 1 +0\cdot 1 +1 \cdot 1=3 \\ & \cdots \\ M_{2,2} = 1\cdot1+ 0\cdot 1+1 \cdot 1+0 \cdot 1 + & 1 \cdot 1 + 0 \cdot 1+ 1\cdot 1 +0\cdot 1 +1 \cdot 1=5 \\ & \cdots \\ M_{3,3} = 1\cdot1+ 0\cdot 1+1 \cdot 0+0 \cdot 1 + & 1 \cdot 1 + 0 \cdot 0+ 1\cdot 0 +0\cdot 0 +1 \cdot 0=2 \end{aligned} \end{gather}\]

La elección de unos u otros valores del filtro dará lugar a matrices de salida que realcen o suavicen ciertas partes de la entrada. Por ejemplo, si la entrada es una imagen, es posible definir filtros que realcen los bordes, que los suavicen o incluso que detecten dichos bordes y cómo de marcados están. La Fig. 37.3 muestra el resultado de aplicar distintos filtros a una imagen de entrada.

Figura 37.3: Resultado de aplicar diferentes filtros de convolución sobre una imagen dada.

Los valores (o pesos) de los filtros se ajustaban tradicionalmente de forma manual según el problema a resolver. En los frameworks actuales se ajustan durante el proceso de entrenamiento de la CNN junto con el resto de pesos de la red, lo cual permite encontrar los valores del filtro que maximicen la precisión de la red.

37.3 Neuronas convolucionales

Las capas convolucionales de la CNN no están compuestas por perceptrones, sino por neuronas convolucionales que aplican los filtros de convolución sobre la salida de la capa anterior. Por tanto, los pesos de estas neuronas convolucionales se organizan en forma de matriz, siendo cada matriz un filtro. Cada neurona da lugar a una matriz cuyos valores pasarán por la función de activación para obtener finalmente lo que se conoce como mapa de activaciones. Por tanto, la salida de una capa convolucional compuesta por varias de estas neuronas está formada por un conjunto de estos mapas y tiene forma de matriz 3D (Fig. 37.4).

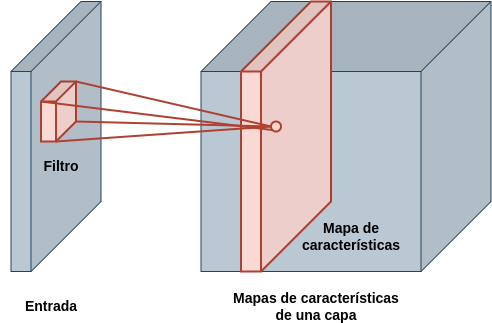
Figura 37.4: Conjunto de mapas de activaciones de una determinada capa (cada filtro de la capa da lugar a un mapa diferente).

Al igual que los perceptrones, las neuronas convolucionales incluyen términos independientes que se suman al resultado de realizar la convolución con el filtro. Por ejemplo, una capa con 64 filtros de tamaño 7 \(\times\) 7 tendrá 64 de estos valores, uno para cada filtro. A estos valores se les conoce también con el nombre de bias. Por tanto, la salida de una neurona convolucional, \(\bf Y\), se obtiene como sigue:

\[\begin{equation} {\bf Y} = g ({ \bf F} \otimes {\bf E} + {\bf B}) , \end{equation}\]

donde \(\bf E\) es la matriz de la entrada, \(\bf F\) es la matriz que representa el filtro, \(g\) es la función de activación y \(\bf B\) es una matriz de términos independientes, con todos los valores iguales.

La mayoría de las CNN utilizan la ReLU como función de activación, o alguna variante de esta. Esta función de activación funciona muy bien con el método del descenso del gradiente que se utiliza para actualizar los pesos.

En el caso de que la entrada no sea una matriz 2D sino una matriz 3D como, por ejemplo, una imagen con varios canales de color o un conjunto de mapas de activación, los filtros contarán con una tercera dimensión. La Fig. 37.5 muestra el resultado de aplicar un filtro de tamaño \(3 \times 3 \times 3\) sobre una imagen con 3 canales de color antes y después de pasar por una función de activación de tipo ReLU.

Figura 37.5: Resultado de aplicar un filtro 3D a una imagen antes y después de pasar por el filtro de activación.

37.4 Relleno del borde

Si se aplica el filtro convolucional a una entrada, la matriz resultante será algo más pequeña ya que no se puede centrar el filtro en los bordes de la matriz. Para poder hacerlo, se suele incrementar la entrada con un relleno (en inglés padding). El relleno se puede realizar con ceros, con algún valor, con el valor más cercano del borde, etc. La Fig. 37.6 muestra algunos de los rellenos más empleados.

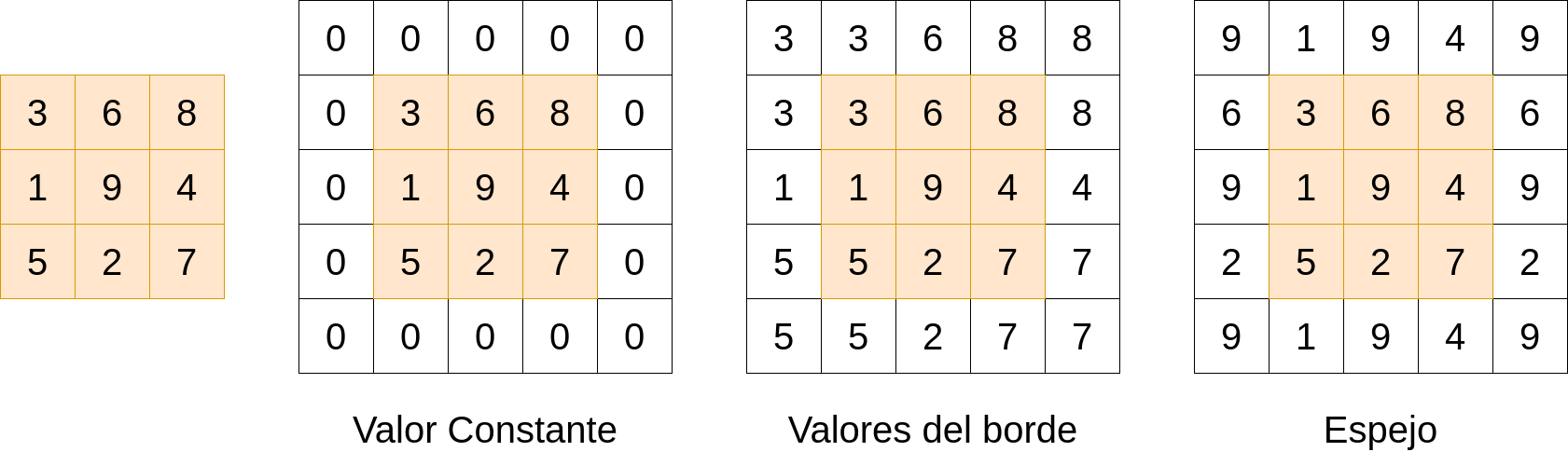
Figura 37.6: Distintos tipos de relleno del borde.

37.4.1 Desplazamiento

El desplazamiento (en inglés stride) básico con el que se aplica un filtro convolucional es de 1. Sin embargo, la aplicación de muchos filtros repartidos en capas a lo largo de la red hace que sea especialmente difícil mantener todos los datos generados en un momento determinado del entrenamiento. Para reducir este volumen de datos, se suelen aplicar las convoluciones con un desplazamiento mayor que 1. Esto reduce el tamaño del mapa de activaciones obtenido por una determinada capa (véase Fig. 37.7).

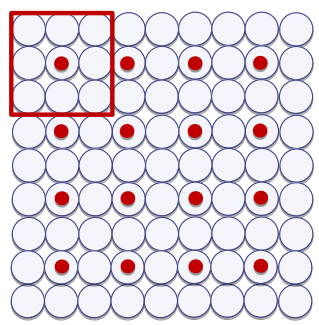
Figura 37.7: Desplazamiento 2 x 2 del filtro. El punto es el centro de la zona en la que se aplica el filtro en cada momento.

37.5 Capas de agrupación

La ejecución en secuencia de varias capas convolucionales es muy efectiva a la hora de decidir si ciertas características están o no presentes en la entrada. Sin embargo, una de sus ventajas, y a la vez una de sus limitaciones, es que mantiene la localización espacial de las características. Aunque es necesaria cierta información espacial como, por ejemplo, el que hubiera unos bigotes cerca de una boca sería característico de una imagen que contuviese un gato, pequeños movimientos del contenido de la imagen producirían mapas de características diferentes.

Una forma de mitigar este problema es usar capas de agrupación (en inglés pooling). Estas capas agrupan un número de valores adyacentes de los mapas de características obteniendo un nuevo conjunto de mapas más pequeños. Es posible emplear distintos tipos de operaciones con las que realizar la agrupación. Los más empleados suelen ser el max pooling y el average pooling (Goodfellow et al., 2016), que seleccionan el máximo de los valores o su media, respectivamente (Fig. 37.8). El tamaño más típico es 2 \(\times\) 2.

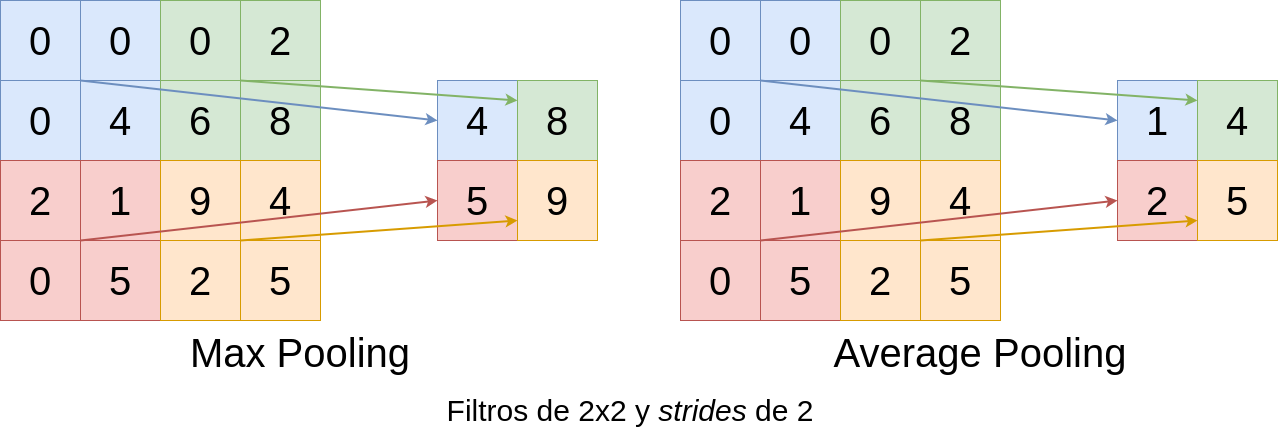
Figura 37.8: Resultado de emplear dos métodos de agrupación diferentes para reducir la dimensión de los datos.

37.6 Desvanecimiento del gradiente

La primera red convolucional fue propuesta en 1982 (Fukushima & Miyake, 1982). Esta arquitectura recibió el nombre de Neocognitron y ya constaba de capas convolucionales y capas de pooling. Siguiendo la misma idea, en 1998 se diseñó otra CNN para resolver el problema de reconocimiento de dígitos manuscritos, MNIST (LeCun et al., 1998). A esta arquitectura de CNN se la conoce con el nombre de LeNet y es una de las arquitecturas más pequeñas que se puede definir para resolver un problema de clasificación (Fig. 37.9). El extractor de características consta de dos capas convolucionales alternadas con 2 capas de pooling que obtienen un total de 400 variables. La parte final con el clasificador está compuesta por 3 capas densas de 120, 84 y 10 neuronas.

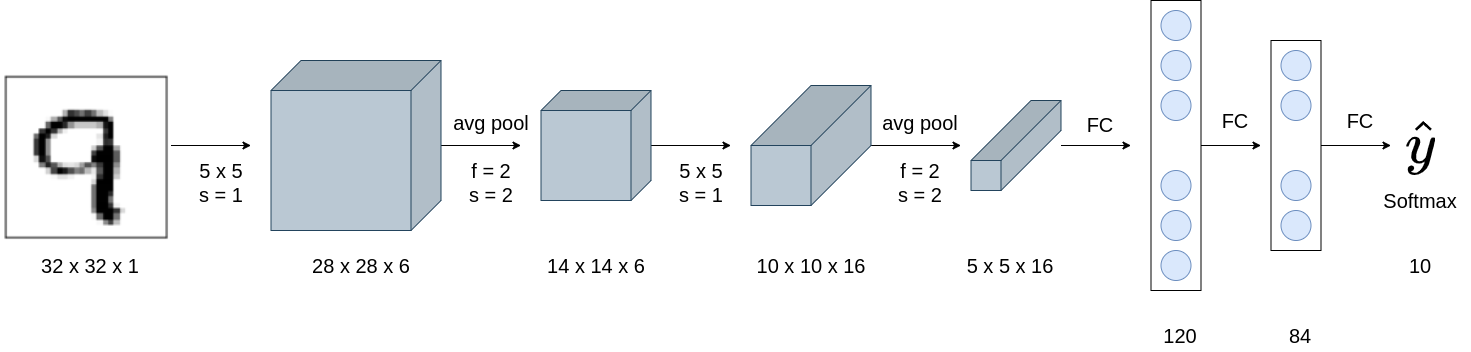
Figura 37.9: Arquitectura LeNet.

A pesar de los buenos resultados obtenidos por la arquitectura, el uso de estos métodos para resolver problemas reales estaba aún lejos debido a la carga computacional requerida para su entrenamiento. No fue hasta el año 2012, cuando los ganadores del concurso ImageNet Challenge presentaron una nueva arquitectura llamada AlexNet, que las CNN volvieron a estar en el punto de mira de los investigadores (Deng et al., 2012). A partir de ese momento, y teniendo en cuenta los grandes avances computacionales de las tarjetas gráficas (GPU), que permitían ejecutar operaciones matriciales de forma eficiente, se empezaron a desarrollar cada vez más arquitecturas diferentes.

Durante los primeros años, las arquitecturas desarrolladas tenían cada vez más capas y más filtros en cada una de ellas para extraer la mayor cantidad de información posible de la entrada. Sin embargo, las arquitecturas más profundas se encontraron con un problema: el desvanecimiento del gradiente.

Ciertas funciones de activación como, por ejemplo, la sigmoide, comprimen el espacio de entrada entre 0 y 1. Esto hace que grandes cambios en la entrada produzcan cambios muy pequeños en la salida, haciendo que la derivada sea pequeña. Como los gradientes de la red se calculan durante la propagación hacia atrás, capa a capa, siguiendo la regla de la cadena, si los valores son muy cercanos a 0, la multiplicación de muchos de estos valores hará que el gradiente de la red caiga rápidamente. Un gradiente muy pequeño hará que los pesos de las capas iniciales apenas se modifiquen con cada iteración y no lleguen a obtener valores adecuados durante el entrenamiento.

Algunas soluciones a este problema son:

• El uso de activaciones tipo ReLU, cuya derivada no genera valores muy pequeños.

• Capas de normalización. Si se normalizan los datos de entrada ya no habrá grandes cambios entre ellos y los valores estarán lejos de los extremos de la sigmoide.

• Uso de bloques con conexiones residuales que añaden (o concatenan) el valor de la entrada del bloque a su salida. Esta estrategia se utiliza en las arquitecturas tipo ResNet. Para más detalles, véase Alarcon Vargas (2022).

37.7 Sobreajuste

Cuanto mayor es el número de parámetros de la red, mayor probabilidad hay de que ``memorice” los datos de entrenamiento. Esto se debe a la cantidad de características que la red es capaz de extraer y medir. Si la red es muy profunda, aprenderá cosas muy concretas del conjunto de entrenamiento, lo que dará lugar a modelos que no generalizan bien con nuevos datos (Tetko et al., 1995).²⁵¹

Además de esto, la no linealidad que añaden las funciones de activación puede hacer que se encuentren fronteras de decisión que modelen datos que no son linealmente separables, pero también facilita que se produzca el sobreajuste (Fig. 37.10).

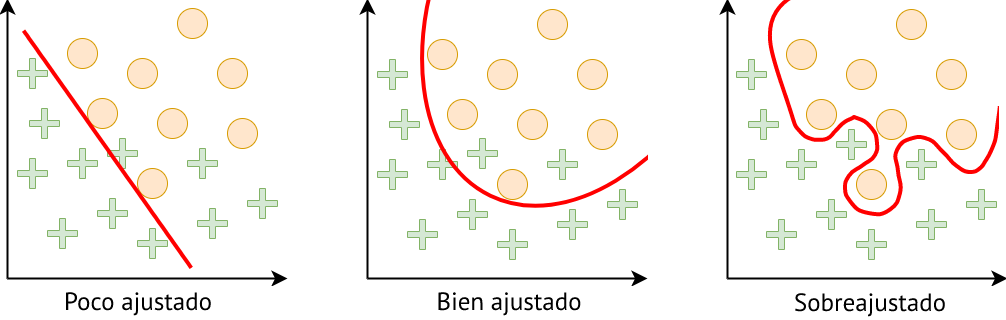
Figura 37.10: Tipos de ajuste del modelo a los datos.

Para evitar que se produzca el sobreajuste se suelen emplear técnicas de regularización. Se trata de técnicas que impiden que los modelos sean demasiado complejos mejorando su capacidad de generalización. Algunas de estas técnicas son:

• Dropout. Durante el entrenamiento, algunas activaciones se ponen a 0 de forma aleatoria (entre el 10% y el 50%). Esto hace que una capa de la red no dependa siempre de los mismos nodos anteriores.

• Early Stopping. Se trata de parar el entrenamiento antes de que se produzca el sobreajuste y seleccionar ese modelo como final. Para ello se utilizan dos conjuntos: uno de entrenamiento y otro de validación. Cuando las curvas de pérdida de ambos conjuntos comienzan a divergir, se para el entrenamiento y se selecciona el modelo resultante del momento anterior al comienzo de la divergencia (Fig. 37.11).

• Regularización L1. Penaliza los pesos grandes, por lo que fuerza a los pesos a tener valores cercanos a 0 (sin ser 0). Añade un término de penalización a la función de coste sumando todos los pesos de la matriz y multiplicado por el valor de \(\alpha\), otro hiperparámetro:²⁵²

\[\begin{equation} \alpha||\boldsymbol W||_1 = \alpha\sum_i\sum_j|w_{ij}| . \end{equation}\]

• Regularización L2 o weight decay. Es parecida a la regularización L1, pero con una expresión algo diferente:

\[\begin{equation} \frac{\alpha}{2} ||\boldsymbol W||_2^2 = \frac{\alpha}{2}\sum_i\sum_j w^2_{ij} . \end{equation}\]

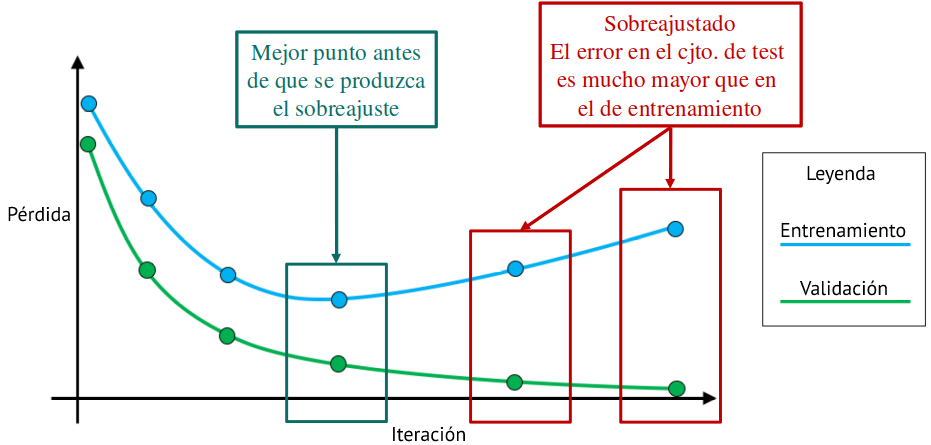
Figura 37.11: Selección del modelo antes del sobreajuste.

37.8 Generación de datos de entrenamiento artificiales

Como se ha comentado anteriormente, las técnicas de deep learning suelen requerir de gran cantidad de datos para su correcto funcionamiento. En muchas situaciones, se dispone de un conjunto limitado para poder entrenar los modelos de forma correcta, por lo que para tratar de suplir la falta de datos se recurre a la generación de datos artificiales, mediante técnicas de data augmentation (en la literatura en español también se denominan con su nombre en inglés) (Shorten & Khoshgoftaar, 2019).

Esta técnica realiza pequeñas variaciones en los datos del conjunto de entrenamiento del que se dispone para obtener datos adicionales, manteniendo el significado semántico de los mismos. También permite mejorar la generalización de los modelos. Por ejemplo, si se tienen imágenes donde una de ellas contiene un elemento de la clase “gato”, las modificaciones que se realicen deben permitir poder reconocer esa misma clase a partir de las imágenes modificadas.

Algunos ejemplos de técnicas de data augmentation en imagen pueden ser: la realización de rotaciones, modificación del contraste o cambios en la iluminación, reescalados, adición/eliminación de ruido o cambio en las proyecciones de las mismas (Fig. 37.12).

Figura 37.12: Ejemplos de técnicas de generación de datos artificiales.

Para utilizar las técnicas de data augmentation en R, se pueden incluir capas específicas de preprocesado durante la definición del modelo, que serán ejecutadas durante el entrenamiento de forma aleatoria. Es decir, cada vez que el proceso de entrenamiento necesite una imagen, decidirá de forma aleatoria si aplicar cada una de las capas o no. En el siguiente ejemplo se realizan rotaciones aleatorias, volteados horizontales y acercamientos a la imagen:

data_augmentation <-
  keras_model_sequential() |>
  layer_random_rotation(0.1) |>
  layer_random_flip("horizontal") |>
  layer_random_zoom(0.1)

A continuación se muestran los diferentes tipos de preprocesado disponibles para imagen y redes neuronales convolucionales:

layer_random_crop()
layer_random_flip()
layer_random_flip()
layer_random_translation()
layer_random_rotation()
layer_random_zoom()
layer_random_height()
layer_random_width()
layer_random_contrast()

NOta

Otros tipos de data augmentation disponibles en keras y R para otro tipo de datos pueden consultarse en:

https://tensorflow.rstudio.com/guides/keras/preprocessing_layers

37.9 Ejemplo en R para el conjunto de datos CIFAR10

En esta sección se entrena una red neuronal convolucional para clasificar las observaciones (imágenes) contenidas en el conjunto de datos CIFAR10 en las correspondientes clases. Cada una de las imágenes contenidas en el conjunto de datos contiene un único elemento que puede ser clasificado como avión, coche, pájaro, gato, ciervo, perro, rana, caballo, barco o camión. La descarga de los datos debe hacerse a través del enlace https://drive.google.com/file/d/1-pFGg-bkooss1fNp5UNYR0-hLUmDP_XO/view?usp=sharing y tiene que guardarse en una carpeta data dentro del proyecto de trabajo para asegurar la reproducibilidad del ejemplo.

Nota

Existe otra versión del conjunto de datos, denominada como CIFAR100, en la cual se definen un total de 100 posibles categorías en las que pueden ser clasificadas las imágenes que contiene: https://www.rdocumentation.org/packages/keras/versions/2.9.0/topics/dataset_cifar100

Cada una de las imágenes contenidas en el conjunto tiene un tamaño de 32 \(\times\) 32 píxeles en color, representándose mediante los 3 canales RGB, lo cual lo hace diferente del ejemplo del Cap. 36, en el cual se trabaja con imágenes en escala de grises y, por tanto, con un único canal.

A continuación se exponen los pasos que llevan desde la carga y visualización de los datos hasta determinar el rendimiento de la red con las imágenes del conjunto de test, pasos similares a los ya descritos en el Cap. 36, pero adaptando la red al tipo de dato utilizado.

37.9.1 Carga y visualización de los datos

El primer paso es cargar la librería keras, para crear las redes neuronales necesarias y cargar el conjunto de imágenes CIFAR10, que se encuentra disponible públicamente:

library(keras)
load("data/cifar10.RData")

A continuación, se ve (o comprueba) el contenido de las variables generadas, pudiéndose observar que el conjunto de datos CIFAR10 ya viene separado en dos subconjuntos: el de entrenamiento y el de test. El conjunto de entrenamiento está compuesto por 50.000 imágenes y el de test por 10.000. En ambos casos, estas imágenes se almacenan en la variable x.

names(cifar)
#> [1] "train" "test"
dim(cifar$train$x)
#> [1] 50000    32    32     3
dim(cifar$train$y)
#> [1] 50000     1
dim(cifar$test$x)
#> [1] 10000    32    32     3
dim(cifar$test$y)
#> [1] 10000     1

Además, las imágenes de cada subconjunto tienen definida la clase a la que pertenecen; en este caso, cualquiera de las 10 clases indicadas anteriormente. En ambos subconjuntos, esta etiqueta se almacena en la variable y. A continuación, se muestra un pequeño ejemplo que permite mostrar alguna de las imágenes contenidas en el conjunto de datos de entrenamiento junto con su etiqueta (Fig. 37.13):

class_names <- c('avion', 'coche', 'pajaro', 'gato', 'ciervo',
               'perro', 'rana', 'caballo', 'barco', 'camion')
index <- 1:30

par(mfcol = c(5,6), mar = rep(1, 4), oma = rep(0.2, 4))
cifar$train$x[index,,,] |> 
  purrr::array_tree(1) |>
  purrr::set_names(class_names[cifar$train$y[index] + 1]) |> 
  purrr::map(as.raster, max = 255) |>
  purrr::iwalk(~{plot(.x); title(.y)})

Figura 37.13: Imágenes del conjunto de datos de entrenamiento con su etiqueta.

37.9.2 Preprocesamiento

Una vez cargados los datos y comprobado su contenido, igual que en el Cap. 36, se puede realizar algún tipo de preprocesado. Al estar trabajando con imágenes, es muy típico estandarizar sus valores de color para mitigar las diferencias producidas por las diferentes condiciones de iluminación.

En este caso, también igual que en el Cap. 36, se transforman los valores originales de la imagen (en rango de 0 a 255) a valores entre 0 y 1 dividiendo cada valor por el máximo, 255:

cifar$train$x <- cifar$train$x/255
cifar$test$x <- cifar$test$x/255

37.9.3 Generación de la red neuronal

La CNN se crea en dos pasos, para, además, mostrar cómo se pueden utilizar las funciones proporcionadas por la librería keras para definir una CNN en varias partes, combinándolas poco a poco.

En el primero, se define la base convolucional de la red combinando varias capas Conv2d con MaxPooling2D. Para ello se utiliza la interfaz sequential proporcionada por Tensorflow/Keras a través de la función keras_model_sequential(). Esta es la parte de la red que se encarga de aprender las características que permitirán representar el contenido de la imagen. Otra de las diferencias principales que se puede observar en esta red es que, al aceptar imágenes de 3 canales, RGB, en vez de imágenes en escala de grises, el tamaño de la entrada de la primera capa tiene que reflejar esta circunstancia: input_shape = c(32, 32, 3).

model <- keras_model_sequential() |> 
  layer_conv_2d(filters = 32, kernel_size = c(3,3), activation = "relu", 
                input_shape = c(32,32,3)) |> 
  layer_max_pooling_2d(pool_size = c(2,2)) |> 
  layer_conv_2d(filters = 64, kernel_size = c(3,3), activation = "relu") |> 
  layer_max_pooling_2d(pool_size = c(2,2)) |> 
  layer_conv_2d(filters = 64, kernel_size = c(3,3), activation = "relu")

Como se puede observar, en esta parte de la red se reduce la dimensión de la información de manera paulatina en cada capa, obteniendo las características representativas del objeto contenido en cada imagen hasta llegar a un tamaño de \(4\times 4\times 64\).

summary(model, line_length=74)
#> Model: "sequential_2"
#> __________________________________________________________________________
#>  Layer (type)                    Output Shape                 Param #     
#> ==========================================================================
#>  conv2d_2 (Conv2D)               (None, 30, 30, 32)           896         
#>  max_pooling2d_1 (MaxPooling2D)  (None, 15, 15, 32)           0           
#>  conv2d_1 (Conv2D)               (None, 13, 13, 64)           18496       
#>  max_pooling2d (MaxPooling2D)    (None, 6, 6, 64)             0           
#>  conv2d (Conv2D)                 (None, 4, 4, 64)             36928       
#> ==========================================================================
#> Total params: 56,320
#> Trainable params: 56,320
#> Non-trainable params: 0
#> __________________________________________________________________________

Ahora, se añaden capas que transformen los resultados de la parte convolucional de la red implementada en la probabilidad de que la imagen represente cada una de las posibles clases.

Para ello, primero se inserta una capa de tipo flatten que se encarga de transformar la salida de la última capa convolucional \(4\times4\times64\) a un vector de 1.024 elementos. A continuación, una capa oculta dense de 64 neuronas con activación relu se encarga de realizar las primeras operaciones con esos datos y de reducir la dimensionalidad. Finalmente, una última capa dense con activación softmax se encarga de obtener la probabilidad de que la imagen represente cada una de las 10 posibles clases:

model |> 
  layer_flatten() |> 
  layer_dense(units = 64, activation = "relu") |> 
  layer_dense(units = 10, activation = "softmax")

A continuación se muestra la estructura final del modelo implementado:

summary(model, line_length=74)
#> Model: "sequential_2"
#> __________________________________________________________________________
#>  Layer (type)                    Output Shape                 Param #     
#> ==========================================================================
#>  conv2d_2 (Conv2D)               (None, 30, 30, 32)           896         
#>  max_pooling2d_1 (MaxPooling2D)  (None, 15, 15, 32)           0           
#>  conv2d_1 (Conv2D)               (None, 13, 13, 64)           18496       
#>  max_pooling2d (MaxPooling2D)    (None, 6, 6, 64)             0           
#>  conv2d (Conv2D)                 (None, 4, 4, 64)             36928       
#>  flatten_1 (Flatten)             (None, 1024)                 0           
#>  dense_7 (Dense)                 (None, 64)                   65600       
#>  dense_6 (Dense)                 (None, 10)                   650         
#> ==========================================================================
#> Total params: 122,570
#> Trainable params: 122,570
#> Non-trainable params: 0
#> __________________________________________________________________________

Nota

Un detalle a tener en cuenta con respecto al ejemplo del Cap. 36 es la variable Total params. Este valor indica el número de parámetros que contiene la red neuronal y, en cierta manera, el tamaño de la misma. Se puede observar que en este caso la CNN tiene 122.570 parámetros, mientras que la red del ejemplo del Cap. 36 tiene 11.935.

Finalmente, es necesario compilar el modelo, indicando algunos de los parámetros de configuración necesarios para el proceso de entrenamiento, como el optimizador a utilizar, la función de coste y las métricas a calcular para poder evaluar la red entrenada:

model |> compile(
  optimizer = "sgd", # stochastic gradient descent
  loss = "sparse_categorical_crossentropy", # función utilizada para problemas de clasificación con varias clases
  metrics = "accuracy" # Precisión
)

37.9.4 Entrenamiento

Una vez generada la estructura de la red neuronal convolucional, ya se puede entrenar, mediante la función fit(), para resolver el problema de clasificación. Para ello, se le debe indicar el conjunto de imágenes de entrenamiento, x, que debe utilizar y sus etiquetas correspondientes, y. Además de otros parámetros, se podrá configurar el número de épocas (epochs, pasadas sobre el conjunto completo de entrenamiento), el tamaño del batch que se utilizará en cada iteración (con batch_size, número de imágenes por iteración), qué porcentaje de elementos del conjunto de datos se utilizarán para validar el modelo (con validation_split, imágenes utilizadas durante el entrenamiento pero solo para obtener una estimación real del error cometido) o la tasa de aprendizaje (learning_rate), entre otros.

training_evolution <- model |> 
  fit(
    x = cifar$train$x, y = cifar$train$y,
    epochs = 10, batch_size = 32,
    validation_split = 0.2,
    learning_rate = 0.1,
    verbose = 2
  )

Nota

Como se puede observar, el batch_size configurado es menor que el del Cap. 36 (32 \(vs.\) 128). Esto es debido a que el número máximo de imágenes que el equipo utilizado para entrenar puede procesar en una iteración viene determinado por el tamaño de la red neuronal, es decir, por la variable Total params indicada en la nota anterior. Cuanto mayor sea el tamaño de la red, menor será el número máximo de imágenes que podrá tener el batch.

#> Epoch 1/10
#> 1250/1250 - 12s - loss: 2.1097 - accuracy: 0.2316 - val_loss: 1.9339 - val_accuracy: 0.2958 - 12s/epoch - 9ms/step
#> Epoch 2/10
#> 1250/1250 - 8s - loss: 1.7478 - accuracy: 0.3667 - val_loss: 1.6987 - val_accuracy: 0.3965 - 8s/epoch - 6ms/step
#> Epoch 3/10
#> 1250/1250 - 8s - loss: 1.5464 - accuracy: 0.4399 - val_loss: 1.4731 - val_accuracy: 0.4707 - 8s/epoch - 7ms/step
#> Epoch 4/10
#> 1250/1250 - 9s - loss: 1.4304 - accuracy: 0.4866 - val_loss: 1.3653 - val_accuracy: 0.5149 - 9s/epoch - 7ms/step
#> Epoch 5/10
#> 1250/1250 - 8s - loss: 1.3477 - accuracy: 0.5199 - val_loss: 1.3407 - val_accuracy: 0.5257 - 8s/epoch - 6ms/step
#> Epoch 6/10
#> 1250/1250 - 7s - loss: 1.2784 - accuracy: 0.5437 - val_loss: 1.2563 - val_accuracy: 0.5564 - 7s/epoch - 6ms/step
#> Epoch 7/10
#> 1250/1250 - 7s - loss: 1.2118 - accuracy: 0.5705 - val_loss: 1.2331 - val_accuracy: 0.5720 - 7s/epoch - 6ms/step
#> Epoch 8/10
#> 1250/1250 - 8s - loss: 1.1539 - accuracy: 0.5954 - val_loss: 1.1807 - val_accuracy: 0.5882 - 8s/epoch - 6ms/step
#> Epoch 9/10
#> 1250/1250 - 7s - loss: 1.1015 - accuracy: 0.6135 - val_loss: 1.1516 - val_accuracy: 0.5935 - 7s/epoch - 6ms/step
#> Epoch 10/10
#> 1250/1250 - 7s - loss: 1.0526 - accuracy: 0.6286 - val_loss: 1.1014 - val_accuracy: 0.6128 - 7s/epoch - 6ms/step

Tras el entrenamiento, se puede observar la evolución del mismo mediante las gráficas de coste/pérdida y precisión (Fig. 37.14).

plot(training_evolution)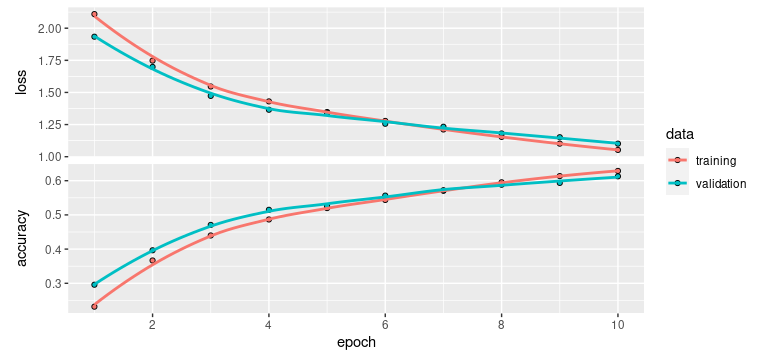

Figura 37.14: Evolución durante el entrenamiento de la precisión y la pérdida: conjuntos de entrenamiento y validación.

Como se puede apreciar, la red entrenada es capaz de alcanzar un 60% de precisión tanto en el conjunto de entrenamiento como en el de validación.

37.9.5 Test

Una vez entrenado el modelo ya se puede aplicarse al conjunto de test. La clasificación de cualquiera de las imágenes en una de las posibles clases se lleva a cabo mediante la función predict(). En realidad, la salida de la función es la probabilidad de que dicha imagen pertenezca a cada una de las posibles clases, clasificándose en aquella para la cual la probabilidad sea mayor:

predictions <- predict(model, cifar$test$x)
head(round(predictions, digits=2), 5)
#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#> [1,] 0.03 0.00 0.18 0.47 0.01 0.14 0.16    0 0.00 0.00
#> [2,] 0.04 0.07 0.00 0.00 0.00 0.00 0.00    0 0.89 0.00
#> [3,] 0.08 0.28 0.00 0.00 0.00 0.00 0.00    0 0.55 0.07
#> [4,] 0.82 0.01 0.04 0.00 0.00 0.00 0.00    0 0.11 0.00
#> [5,] 0.00 0.00 0.05 0.11 0.11 0.03 0.69    0 0.00 0.00

Con la función evaluate() se calculan tanto el coste o pérdida como la precisión de la red neuronal sobre el conjunto de test. Como se puede observar, se obtienen valores muy similares a los que se obtuvieron para el conjunto de entrenamiento:

evaluate(model, cifar$test$x, cifar$test$y, verbose = 0)
#>      loss accuracy
#>  1.094381 0.611100

Con la función predict también se puede generar la matriz de confusión de la red:

prediction_matrix <- model |> predict(cifar$test$x) |> k_argmax()
confusion_matrix <- table(as.array(prediction_matrix), cifar$test$y)
confusion_matrix

#>    
#>       0   1   2   3   4   5   6   7   8   9
#>   0 650  25  57  12  39  12   3  21  82  35
#>   1  43 790  15  18  13  11  16  12  43 179
#>   2 119  20 676 180 325 170 112  94  33  26
#>   3  23  15  57 427  76 184  54  48  18  18
#>   4   1   0  13  20 236  12   5  21   3   2
#>   5   6   7  52 145  41 488  24  82   5  10
#>   6  14   5  71 110 119  42 755  13   4  14
#>   7   7   6  30  46 126  60  16 676   9  18
#>   8 114  58  15  19  20  13   6   5 777  62
#>   9  23  74  14  23   5   8   9  28  26 636

37.9.6 Otros ejemplos de interés

Otros ejemplos para trabajar en R pueden encontrarse en los siguiente enlaces: (i) Transfer learning and fine tuning, explicación de estas técnicas para clasificar imágenes que contienen perros y gatos https://tensorflow.rstudio.com/guides/keras/transfer_learning (ii) https://tensorflow.rstudio.com/guides/ y (iii) https://tensorflow.rstudio.com/examples/

Resumen

• Este capítulo presenta las principales características de las redes neuronales convolucionales y sus diferencias con el perceptrón multicapa.

• Además, se exponen los principales problemas a la hora de diseñar este tipo de redes profundas y se plantean sus posibles soluciones.

• Finalmente, se exponen los pasos necesarios para entrenar y poner en práctica una red neuronal convolucional en R, con la librería Tensorflow/Keras, que clasifique las imágenes del conjunto de datos CIFAR10 en 10 posibles clases.