Capítulo 16 Modelos lineales generalizados

Víctor Casero-Alonso\(^{a}\) y María Durbán\(^{b}\)

\(^{a}\)Universidad de Castilla-La Mancha
\(^{b}\)Universidad Carlos III de Madrid

16.1 Introducción

Como se ha mencionado en el Cap. 15 de modelización lineal, el objetivo detrás del uso de modelos es el de intentar explicar el comportamiento de una variable en función del comportamiento de otras que se cree que influyen en ella. Por ejemplo, podría interesar predecir:

• si un empleado abandonará la empresa, o no, en función de sus años de experiencia, su formación, etc.; o si un paciente sufrirá, o no, una enfermedad en función de su edad, sexo, nivel de colesterol, etc.,

• el número de días que un empleado puede estar de baja laboral en función del tipo de enfermedad, su antigüedad, salario, etc.; o el número de días que un paciente puede estar hospitalizado en función de la dolencia por la que acude a urgencias, su edad, sexo, etc.

Estos casos no pueden analizarse correctamente con el modelo de regresión lineal múltiple visto en el Cap. 15 porque la variable respuesta, la que interesa predecir en cada ejemplo, no sigue una distribución de probabilidad normal (supuesto necesario para utilizar la regresión lineal) o ni siquiera es continua. Concretamente:

• abandonar, o no, la empresa o sufrir, o no, una enfermedad se puede modelizar mediante una variable dicotómica/binaria asignando los valores 0 y 1 a las dos posibles respuestas, lo que encaja perfectamente con una distribución de probabilidad de Bernoulli (muy distinta de la normal, ya que es discreta, aunque podría parecerse; véase Cap. 12,

• el número de días de baja (en empleados), de hospitalización (en pacientes)… son variables de tipo recuento (solo cero o valores positivos) modelizables mediante una variable discreta que podría seguir una distribución de Poisson (que es también distinta a la normal, por ser discreta, aunque también podría parecerse).

En este capítulo se aborda el modelo lineal generalizado (GLM), que generaliza el caso en que la variable respuesta sea normal a cualquier tipo de distribución de probabilidad perteneciente a la familia exponencial y que permite varianzas no constantes en los errores. En concreto, se centra en la regresión logística y la regresión de Poisson, casos particulares de este modelo, que permiten modelizar correctamente los dos casos planteados anteriormente. Un buen libro de referencia para este capítulo es James et al. (2013).

16.2 El modelo y sus componentes

El modelo lineal generalizado¹²⁷ se puede escribir como: \[\mu = g^{-1}(\eta),\] en el que se tienen los siguientes componentes:

1. \(\mu=E(Y)\), el componente aleatorio: la media de la variable respuesta Y, que puede seguir cualquier distribución de probabilidad de la familia exponencial. Entre ellas están las más habituales: la normal (por tanto, el modelo de regresión lineal es un caso particular del GLM), la Bernoulli/binomial (utilizada en la regresión logística), la Poisson, la gamma, etc.

2. \(\eta = X \beta\), el componente sistemático, el predictor lineal, la “estructura” que aportan las variables explicativas/predictoras \(X=(X_1, \ldots , X_p)\), que intentan explicar el comportamiento de la variable respuesta, donde \(\beta=(\beta_1, \ldots , \beta_p)\) es el vector de coeficientes (parámetros) a estimar del modelo.

3. \(g(\cdot)\), la novedad de los GLM, la denominada función de enlace, que relaciona los dos componentes anteriores. Esta función puede tomar distintas formas, como se verá en la siguiente sección.

Igual que en el modelo lineal, las dos partes o etapas fundamentales del análisis de un GLM son:

1. La especificación de la relación o estructura predefinida de antemano, mediante la estimación de los coeficientes que mejor ajustan dicha relación, utilizando el método de máxima verosimilitud¹²⁸. Más adelante se verá cómo se interpretan tales coeficientes y cómo se puede comprobar la adecuación del modelo.
2. La utilización del modelo estimado (especificado) para predecir nuevas respuestas, según sea el caso: valores, probabilidades de ocurrencia, etc.

Para la correcta aplicación de los GLM es crucial la elección tanto de la variable respuesta como de las explicativas (que podrían ser de distinto tipo: numéricas –continuas o discretas– o categóricas/cualitativas –dicotómicas o politómicas–¹²⁹), así como de la distribución de probabilidad más apropiada para la respuesta. Como se adelantó en el Cap. 15, como muestra sirva percatarse de que una misma variable podría ser explicativa o respuesta, por ejemplo “diabetes” (sí o no), según se tenga interés en explicar la influencia de la diabetes en otra variable o la influencia de otras variables en la diabetes. También una misma variable podría considerarse y utilizarse como variable de distinto tipo; por ejemplo, la edad puede considerarse como variable discreta (años cumplidos) o como categórica ordinal (grupos de edad), aunque es una variable continua (puede tomar cualquier valor en un intervalo).

16.2.1 Función enlace

Cada distribución de probabilidad tiene asociada una función de enlace canónica:¹³⁰

• Para la normal es la identidad: \(g(\mu)=\mu\).
• Para la de Bernoulli, es la función logit: \(g(\mu)=logit(\mu)=log (\mu / (1-\mu))\).
• Para la Poisson, es el logaritmo: \(g(\mu)=log(\mu)\).
• Para la gamma es la inversa: \(g(\mu)=1/\mu\), …

Tanto en el caso de la regresión logística (variable respuesta tipo Bernoulli) como en la regresión de Poisson aparece el logaritmo (neperiano) en la función de enlace, lo que conduce a efectos multiplicativos de los factores o covariables \(X_i\) sobre la respuesta, como se verá más claramente en la Sec. 16.4.3. Este es un punto que las distingue de la regresión lineal, en la que los efectos son aditivos.

16.3 Procedimiento con R: la función glm()

En el paquete stats (de la distribución base de R) se encuentra la función glm() que se utiliza para llevar a cabo el ajuste de un GLM:

glm(formula, family = ..., data = ..., ...)

• formula: para definir el predictor lineal; por ejemplo, Y ~ X1 + X2 + X3.
• family: para indicar la distribución de la variable respuesta (gaussian, binomial, poisson …) que determina la función de enlace (binomial \(\rightarrow\) logit, etc.; consúltese ?family o ?glm para más detalles).

Las “herramientas” utilizadas para lm() también se pueden usar para glm() (aunque algunas interpretaciones varían). Así, se puede usar summary() para detectar los predictores importantes, fitted() para obtener los valores ajustados, etc.

16.4 Regresión logística

La regresión logística es el caso más “famoso” de GLM, de gran relevancia en distintos contextos: Medicina, Economía, etc. Se utiliza cuando la variable respuesta es dicotómica, del tipo pertenencia, o no, a un determinado grupo (fumadores, enfermos, morosos, …). Habitualmente se considera que toma el valor \(Y=1\) si la observación pertenece al grupo de interés e \(Y=0\) en caso contrario. Tal tipo de variable se puede modelizar con una distribución de Bernoulli, caracterizada por un parámetro \(p\) que indica la probabilidad de pertenecer al grupo de interés.

El objetivo principal suele ser predecir el grupo al que pertenece un nuevo individuo/elemento, sobre la base de la información sobre dicho elemento/individuo que proporcionan las variables explicativas. Para ello, se estima el modelo con los datos disponibles, determinándose qué variables influyen significativamente en la variable respuesta.¹³¹

¿Por qué no tiene cabida aquí el uso del modelo de regresión lineal múltiple? Al ajustar un modelo del tipo: \(Y=\beta_0 + \beta_1 X_1 + \ldots + \beta_p X_p + \epsilon,\) las estimaciones \(\hat{Y}\) serán números reales que rara vez coincidirán con 0 o 1 (que son los valores admisibles de la variable respuesta). Dicho de otro modo, si solo se tuviese una variable explicativa, al ajustar el modelo de regresión lineal simple, la recta sobrepasaría, o no alcanzaría, los valores posibles de respuesta (0 o 1), como ocurre en la Fig. 16.1 (izquierda) obtenida a partir de los datos del ejemplo de enfermedad coronaria que se manejará en la Sec. 16.6.1.

El modelo de regresión logística múltiple se define como: \[\begin{equation} \text{logit}(p)=\log{ \Big(\dfrac{p}{1-p} \Big)}=\beta_0 + \beta_1 X_1 + \ldots + \beta_p X_p + \epsilon, \tag{16.1} \end{equation}\] que permite estimar la ratio entre la probabilidad de pertenecer al grupo de interés, \(p\), y la de no pertenecer a dicho grupo, \(1-p\). Utilizando la función de enlace se puede transformar el predictor lineal \(\eta=\beta_0 + \beta_1 X_1 + \ldots + \beta_p X_p\) para obtener valores admisibles para una probabilidad. La función logística, definida como \[\begin{equation} p = \frac{e^\eta}{1+e^\eta} \tag{16.2} \end{equation}\] y representada en la Fig. 16.1 (derecha), es la más habitual, y por ello da el nombre a la regresión logística. Con ella se obtiene la probabilidad de pertenecer al grupo de interés, \(p = P[Y = 1]\), e inmediatamente la de no pertenecer a dicho grupo, \(1-p = P[Y = 0]\).

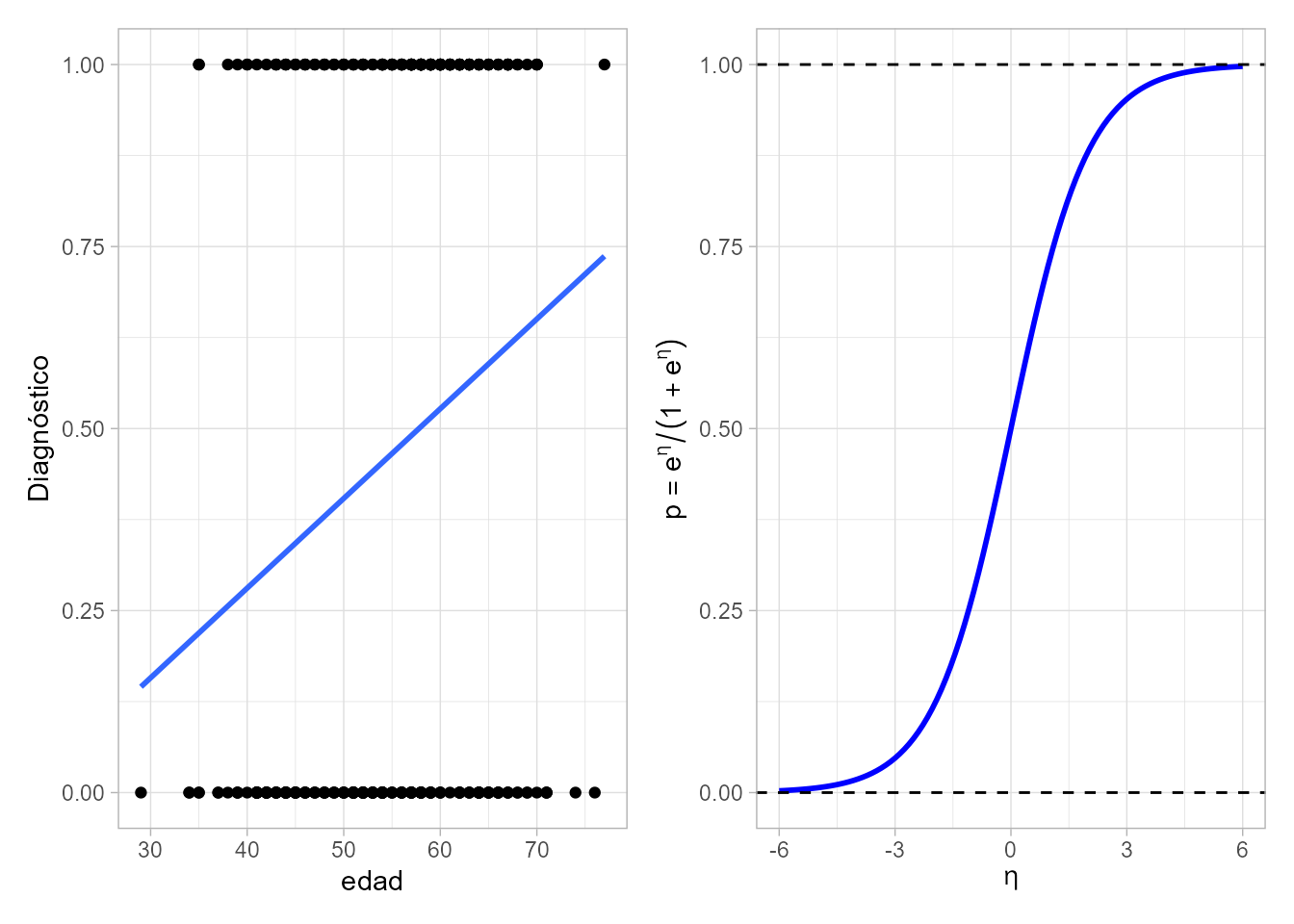
Figura 16.1: Gráfico de dispersión del diagnóstico frente a la edad para el ejemplo de enfermedad coronaria (izquierda) y función logística (derecha).

La ventaja del modelo logístico es que la función logística tiende a cero por la izquierda y a uno por la derecha, por lo que la predicción será siempre un valor válido para una probabilidad. Como contrapartida, a medida que las probabilidades se acercan a cero o a uno la relación entre el predictor y la probabilidad deja de ser lineal, lo que complica la interpretación de los coeficientes.

16.4.1 Procedimiento de ajuste

A partir de los datos disponibles de las variables predictoras y respuesta:

1. Se estiman los coeficientes \(\beta_j\) del modelo, para especificar la relación entre las variables, contrastando si tales estimaciones, \(\hat\beta_j\), son o no significativas.
2. Se valora la eliminación de variables no significativas, atendiendo a la significación global del modelo, al modelo teórico subyacente, etc.
3. Se comprueba la adecuación del modelo final obtenido.
4. En caso afirmativo, se interpretan los coeficientes y el modelo queda listo para hacer predicciones de probabilidades o para clasificar individuos/elementos.

Nota

Como se menciona en el Cap. 15, un coeficiente es significativo cuando su p–valor asociado es lo suficientemente pequeño (como norma general, inferior a 0,05). No obstante, pueden tomarse otros valores de referencia; por ejemplo, en las salidas de R aparecen otros tres niveles de referencia, 0,1, 0,01 y 0,001.

16.4.2 Adecuación del modelo

Para comprobar si el modelo estimado es adecuado, se compara con el modelo más simple, el que solo incluye el término independiente. Para ello, se pueden utilizar distintos contrastes basados en la deviance,¹³² una medida que juega el papel de la suma de cuadrados de los residuos. En el modelo de regresión logística, la deviance de un modelo es menos dos veces el logaritmo de la verosimilitud de dicho modelo. La diferencia entre la deviance de un modelo más elaborado y el simple se distribuye como una \(\chi^2\) con tantos grados de libertad como restricciones impuestas a los parámetros, lo que permite contrastar cuál de los dos modelos ajusta mejor los datos. P–valores bajos indican que el modelo ajustado es inadecuado, debiendo investigarse otras posibles variables predictoras, si se incumple la hipótesis de linealidad o existe sobredispersión (por ejemplo, por exceso de ceros).

Adicionalmente, se puede aplicar el contraste de la razón de verosimilitudes. Este test contrasta la significación de cada cada variable predictora, basándose en la deviance que se genera al añadir cada variable secuencialmente al modelo que contiene las anteriores, lo que ayuda a decidir si mantenerla o eliminarla del modelo.

Para contrastar la bondad de ajuste del modelo, el contraste más popular en la literatura es el de Hosmer-Lemeshow, aplicable a modelos con al menos una variable cuantitativa. P–valores bajos indican falta de ajuste.

Continuando con las medidas de bondad de ajuste, en el modelo de regresión logística no tiene sentido calcular el coeficiente de determinación lineal, \(R^2\), pero existen varias alternativas equivalentes para hacerse una idea de la variabilidad de la respuesta explicada por el modelo. Las tres más populares son el pseudo \(R^2\) de McFadden, el \(R^2\) de Cox y Snell (que por construcción no puede alcanzar el 1) y el \(R^2\) de Nagelkerke (una corrección del de Cox y Snell).

16.4.3 Interpretación de resultados

La interpretación de los coeficientes no es tan directa y sencilla como en el modelo lineal. A partir de las estimaciones del predictor lineal \(\hat{\eta}\), modelo (16.1), se puede estimar la probabilidad de que un individuo pertenezca al grupo de interés utilizando la expresión (16.2). Alternativamente se puede estimar el odds, con la siguiente expresión, que se deduce de (16.1): \[\begin{equation} \mathit{odds} = \frac{\hat{p}}{1-\hat{p}} = e^{\hat{\eta}} = e^{\hat{\beta}_0 + \hat{\beta}_1 X_1 + \ldots + \hat{\beta}_p X_p}. \tag{16.3} \end{equation}\] El odds se puede explicar como cuántas veces es más probable pertenecer al grupo de interés (\(Y=1\)) que al otro grupo (\(Y=0\)). Por ejemplo, si \(\hat{p} = 0.75\) el odds es \(0.75/0.25=3\), entonces es tres veces más probable pertenecer al grupo de interés que no pertenecer.¹³³

La ecuación (16.3) se puede expresar, equivalentemente, como: \[\begin{equation} \mathit{odds}=e^{\hat{\beta}_0} \cdot e^{\hat{\beta}_1 X_1} \cdot \ldots \cdot e^{\hat{\beta}_p X_p}. \tag{16.4} \end{equation}\] La interpretación de los \(\hat{\beta}_j\) carece de sentido. Lo interpretable son los \(e^{\hat\beta_j}\), denominados odds ratios (OR). Como el modelo (16.4) es multiplicativo (sus términos aparecen multiplicando, no sumando), por lo que valores de \(e^{\hat{\beta}_j}\) inferiores a 1 implican disminución en el valor del odds –se reduce la probabilidad de pertenecer al grupo de interés respecto a la de no pertenecer– y valores por encima de 1 implican incremento del valor del odds, ceteris paribus.¹³⁴ En concreto, \(100(e^{\hat{\beta}_j}-1)\) indica la variación porcentual en el \(odds\) ante un incremento unitario en la variable explicativa \(X_i\), mientras que \(100(e^{-\hat{\beta}_j}-1)\) indica el cambio porcentual que se opera en el \(odds\) debido a un decremento unitario de dicha variable explicativa, \(ceteris \hspace{0,1cm} paribus\).

El modelo de regresión logística se puede acompañar del denominado riesgo relativo (RR, relative risk). Es una razón de probabilidades como el odds, pero en vez de comparar la probabilidad de pertenecer a un grupo o a otro de la variable respuesta, compara las probabilidades de pertenecer al grupo de referencia (\(Y=1\)) según los valores del predictor categórico \(X_i\). El riesgo relativo es similar al OR de la variable \(X_i\) solo cuando la probabilidad de \(Y=1\) es pequeña; se suele dar como referencia que sea inferior al 10%. Por lo tanto, OR y RR no coinciden siempre.

16.4.4 Predicción. Curva ROC y AUC

Como se ha mencionado anteriormente, el uso habitual de la regresión logística es la predicción, no tanto de probabilidades, sino de la clasificación en un grupo u otro de futuros individuos/elementos en base a la información conocida de ellos a través de las variables explicativas. La regla de clasificación en los grupos depende de la elección del punto de corte de la probabilidad, por ejemplo \(\hat{Y}=1\) si \(\hat p>0,7\) e \(\hat{Y}=0\) en otro caso. Para seleccionar dicho punto de corte, se acude al análisis de los casos clasificados correctamente o no por el modelo ajustado: análisis de la sensibilidad y la especificidad del modelo, a su visualización más popular, la curva ROC (receiver operating characteristic) y la medición del área bajo dicha curva, AUC (area under the curve ROC); véase Cap. 9.

La sensibilidad, o tasa de verdaderos positivos, se define como el cociente entre estos y la suma de los verdaderos positivos y los falsos negativos. La especificidad, o tasa de verdaderos negativos, es el cociente entre estos y la suma de los verdaderos negativos y los falsos positivos. Por consiguiente, la sensibilidad es una medida de la probabilidad de que un caso real positivo (\(Y=1\)) sea clasificado correctamente como positivo por el modelo (\(\hat{Y}=1\)). Equivalentemente, la especificidad es la probabilidad de clasificar correctamente casos negativos.

Gráficamente, se pueden obtener los valores de la sensibilidad y especificidad para distintos puntos de corte (entre 0 y 1). La Fig. 16.2 (izquierda) muestra este gráfico para uno de los casos prácticos.¹³⁵ Pero la forma más popular de analizar la sensibilidad y la especificidad es mediante la curva ROC, que representa, para los distintos puntos de corte considerados, la sensibilidad frente a la tasa de falsos positivos, esto es la 1-especificidad (Fig. 16.2 [derecha]). Su AUC sirve para comparar distintos modelos de regresión logística (u otros modelos con el mismo fin).¹³⁶ Cuanto mayor poder discriminante tenga el modelo, más próxima a la unidad estará la AUC. Un clasificador aleatorio presentaría la curva ROC coincidente con la diagonal, con una AUC de 0,5.

16.5 Regresión de Poisson

Se utiliza cuando la variable respuesta es discreta, solo toma valores no negativos y su distribución de probabilidad es modelizable mediante la distribución de Poisson. Por ejemplo, las variables de tipo “número de”, como la del ejemplo del principio: número de días de hospitalización. El parámetro que caracteriza la distribución de Poisson es \(\lambda\), que representa tanto la media como la varianza de la variable aleatoria (a nivel teórico).

Dados los anteriores condicionantes, en esta tesitura tampoco tiene cabida el modelo de regresión lineal, principalmente porque las estimaciones \(\hat{Y}\) podrían arrojar valores negativos.

De nuevo el objetivo suele ser la predicción: en el ejemplo, el número de días que un (nuevo) paciente estará hospitalizado (\(0, 1, 2, \ldots\)), en base a la información proporcionada por las variables explicativas. Previo a la predicción, se estima el modelo, a partir de los datos disponibles, para determinar las variables explicativas que influyen significativamente sobre la variable respuesta. Y, nuevamente, los efectos serán multiplicativos, dado que la función de enlace es de tipo logarítmico, como se ha visto en la Sec. 16.4.3. Por ello, todo lo visto anteriormente para la regresión logística es válido para la regresión de Poisson.

16.6 Casos prácticos

16.6.1 Ejemplos de regresión logística

Para llevar a cabo estos ejemplos, se utiliza el conjunto de datos cleveland incluido en el paquete CDR que acompaña este libro. Se quiere explicar la variable diag (diagnóstico; dicotómica: 1, ha sufrido una enfermedad coronaria; 0, no la ha sufrido) a partir de otras variables. La variable respuesta diag ya aparece como factor en la base de datos.

Estimación
Primeramente, se considera un primer modelo con dos variables explicativas continuas edad y dep (depresión en el segmento ST):

library("CDR")
reg_log <- glm(diag ~ edad + dep, 
               family = "binomial", data = cleveland)
summary(reg_log)
#> 
#> Call:
#> glm(formula = diag ~ edad + dep, family = "binomial", data = cleveland)
#> 
#> Coefficients:
#>             Estimate Std. Error z value Pr(>|z|)    
#> (Intercept) -3.08080    0.81939  -3.760  0.00017 ***
#> edad         0.03738    0.01476   2.532  0.01134 *  
#> dep          0.86851    0.13791   6.298 3.02e-10 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 417.98  on 302  degrees of freedom
#> Residual deviance: 350.64  on 300  degrees of freedom
#> AIC: 356.64
#> 
#> Number of Fisher Scoring iterations: 4

En la salida se muestran las estimaciones de los coeficientes del modelo (columna Estimate) y su significatividad (columna Pr(>|z|)). En este ejemplo, los dos coeficientes de interés (los correspondientes a edad y dep) son significativos (a un nivel de significación del 5%).

Puede observarse que dicha salida también incluye la null deviance y la residual deviance. La primera indica lo “bien” que predice el modelo sin variables explicativas (tan solo con el término independiente o intercepto); la segunda indica lo “bien” que predice el modelo con variables explicativas. Como se avanzó anteriormente, un contraste Chi-cuadrado permitirá dilucidar si el modelo con variables explicativas predice significativamente mejor que el que solo tiene un término independiente y su predicción, sea cual sea el valor de las variables explicativas, es siempre la media de los valores de la variable respuesta.

Se completa el modelo anterior añadiendo variables categóricas –concretamente, tdolor (politómica, tipo de dolor) y sexo (dicotómica)– para poder incluir más adelante la interpretación de los coeficientes asociados a este tipo de variables. Para su correcta interpretación, se deben introducir en el predictor como variables de tipo factor.¹³⁷ De lo contrario, el procedimiento las considera numéricas, obteniéndose una salida que llevaría a una interpretación errónea.

reg_log2 <- update(reg_log, ~ . + sexo + tdolor)

Adecuación del modelo
Para evaluar la bondad de ajuste de los modelos se lleva a cabo el contraste de Hosmer-Lemeshow:

library("ResourceSelection")
hoslem.test(reg_log$y, reg_log$fitted.values)
#> 
#>  Hosmer and Lemeshow goodness of fit (GOF) test
#> 
#> data:  reg_log$y, reg_log$fitted.values
#> X-squared = 5.631, df = 8, p-value = 0.6885
hoslem.test(reg_log2$y, reg_log2$fitted.values)
#> 
#>  Hosmer and Lemeshow goodness of fit (GOF) test
#> 
#> data:  reg_log2$y, reg_log2$fitted.values
#> X-squared = 4.8171, df = 8, p-value = 0.7769

En ambos casos, los p–valores son “altos”, indicando un ajuste suficiente.

Para realizar el test de la razón de verosimilitudes con R se acude a la función anova():

anova(reg_log2, test = "Chisq")
#> Analysis of Deviance Table
#> 
#> Model: binomial, link: logit
#> 
#> Response: diag
#> 
#> Terms added sequentially (first to last)
#> 
#> 
#>        Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
#> NULL                     302     417.98              
#> edad    1   15.447       301     402.54 8.487e-05 ***
#> dep     1   51.894       300     350.64 5.858e-13 ***
#> sexo    1   23.982       299     326.66 9.726e-07 ***
#> tdolor  3   62.153       296     264.51 2.037e-13 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Las deviances correspondientes a añadir secuencialmente cada variable o factor al modelo que contiene los anteriores permite concluir que dicha inclusión secuencial de tales variables predictoras es significativa respecto a los modelos que no las incluyen.

Para completar, se podría contrastar también el efecto de una variable sobre la respuesta comparando la deviance del modelo con dicha variable y sin ella:

## se elimina edad del segundo modelo
reg_log3 <- update(reg_log2, ~ . - edad)
anova(reg_log3, reg_log2, test = "Chisq")
#> Analysis of Deviance Table
#> 
#> Model 1: diag ~ dep + sexo + tdolor
#> Model 2: diag ~ edad + dep + sexo + tdolor
#>   Resid. Df Resid. Dev Df Deviance Pr(>Chi)   
#> 1       297     274.45                        
#> 2       296     264.51  1   9.9488  0.00161 **
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

El resultado indica que la variable edad se considera un predictor significativo en el modelo. Se deja al lector realizar este ejercicio con las restantes variables, que le llevarán a concluir que todas son predictores significativos.

El valor del pseudo \(R^2\) de McFadden se obtiene como sigue:

null <- glm(diag ~ 1, family = "binomial", data = cleveland)
1 - logLik(reg_log) / logLik(null)
#> 'log Lik.' 0.1611088 (df=3)
1 - logLik(reg_log2) / logLik(null)
#> 'log Lik.' 0.3671819 (df=7)

Para el primer modelo el pseudo \(R^2\) de McFadden es 0,16, mientras que para el segundo es 0,37.

Interpretación de los coeficientes
A continuación se muestran los coeficientes estimados del segundo modelo y sus correspondientes OR (sus exponenciales) que son los interpretables:

summary(reg_log2)
#> 
#> Call:
#> glm(formula = diag ~ edad + dep + sexo + tdolor, family = "binomial", 
#>     data = cleveland)
#> 
#> Coefficients:
#>             Estimate Std. Error z value Pr(>|z|)    
#> (Intercept) -6.67669    1.30016  -5.135 2.82e-07 ***
#> edad         0.05621    0.01828   3.075   0.0021 ** 
#> dep          0.80890    0.16597   4.874 1.10e-06 ***
#> sexo1        1.69477    0.36801   4.605 4.12e-06 ***
#> tdolor2      0.65668    0.67357   0.975   0.3296    
#> tdolor3      0.19465    0.59654   0.326   0.7442    
#> tdolor4      2.58230    0.57549   4.487 7.22e-06 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 417.98  on 302  degrees of freedom
#> Residual deviance: 264.51  on 296  degrees of freedom
#> AIC: 278.51
#> 
#> Number of Fisher Scoring iterations: 5
exp(coef(reg_log2))[-1]
#>      edad       dep     sexo1   tdolor2   tdolor3   tdolor4 
#>  1.057824  2.245432  5.445391  1.928371  1.214880 13.227480

Los coeficientes asociados a las variables continuas son significativos y positivos, por tanto sus OR son significativamente superiores a 1. Indican que, ceteris paribus,

• por cada año más, el odds de padecer la enfermedad frente a no padecerla se incrementa¹³⁸ un 5,78% (al ser el valor del OR asociado a la edad 1,0578). ¿Y cuál sería el incremento en el odds ante un aumento de la edad en 20 años? En tal caso, el odds ser multiplicaría por \(e^{\hat{\beta}_1 \cdot 20}\) = 3,078, es decir, se ha más que triplicado. Se debe ser cuidadoso con la interpretación: no se triplica la probabilidad sino el odds.
• ante un aumento de una unidad en la variable dep se multiplica más del doble el odds del paciente, pues su OR es 2,2454.

Nota

En regresión lineal, que un coeficiente sea significativo quiere decir que es significativamente distinto de cero, por el hecho de que el modelo considera efectos aditivos de las variables. El modelo de regresión logística es de efectos multiplicativos y, por ello, el valor “neutro” es el 1. Por tanto, un coeficiente significativo se interpreta como significativamente distinto de 1.

¿Y cómo se interpretan los coeficientes asociados a las variables categóricas? ¿Qué significan los valores de sexo1, tdolor2…? Representan el cambio (promedio) en la variable respuesta al pasar de la categoría de referencia a la mostrada.¹³⁹

• el de sexo1 significa que el odds de padecer la enfermedad en los hombres (sexo=1) es más de 5 veces superior que en las mujeres (sexo=0).
• el de tdolor4 indica que los individuos con este tipo de dolor (asintomáticos) presentan un odds 13 veces superior al de los de tdolor=1 (angina típica).¹⁴⁰

Nótese que no se muestra \(e^{\beta_0}\), pues su interpretación carece de sentido práctico: sería el OR de las personas de 0 años, dep=0, sexo=0 y tdolor=1.

Predicciones
Una vez estimado el modelo y comprobada su bondad, se puede usar para obtener predicciones. Para ello, se deben asignar valores a las variables explicativas: edad, dep, sexo y tdolor (se han escogido arbitrariamente).

individuo <- data.frame(edad = 50, dep = 3, 
                        sexo = "1", tdolor = "4" #entre comillas por ser factores
                        ) 

Con la función predict() se puede obtener tanto el valor predicho para el predictor lineal (valor no interpretable), \(\eta\), como directamente la probabilidad de que dicho individuo sufra la enfermedad coronaria, \(p\):

#(eta <- predict(reg_log2, individuo))
(p <- predict(reg_log2, individuo, type = "response"))
#>         1 
#> 0.9446843

A partir del valor de \(p\) (o de \(\eta\)) se puede obtener el odds correspondiente:

p / (1 - p) # exp(eta)
#>        1 
#> 17.07805

Es decir, un individuo con 50 años, dep=3, sexo=1 (hombre) y tdolor=4 (asintomático) tiene una probabilidad de padecer la enfermedad en cuestión 17 veces mayor que de no padecerla.

Riesgo relativo
Se ha visto que el OR para la categoría hombre en el segundo modelo es 5,45. El riesgo relativo de sufrir la enfermedad, en el caso de los varones, para un paciente de 50 años, valor dep=3 y tdolor=4 (asintomático) es:

hom <- data.frame(edad = 50, dep = 3, sexo = "1", tdolor = "4")
muj <- data.frame(edad = 50, dep = 3, sexo = "0", tdolor = "4")
(ph <- predict(reg_log2, hom, type = "response"))
#>         1 
#> 0.9446843
(pm <- predict(reg_log2, muj, type = "response"))
#>         1 
#> 0.7582346
ph / pm # riesgo relativo hombre/mujer
#>      1 
#> 1.2459

El riesgo relativo de sufrir la enfermedad, en el caso de los varones, es \(RR\)= 0,9447/0,7582 = 1,2459, es decir, un varón tiene un 24,6% más de posibilidades de tener la enfermedad que una mujer con sus mismos valores o categorías en las variables que se usan como predictores. En este caso, el OR y el RR no son valores cercanos; ello es debido a que el diagnóstico 1 es frecuente (concretamente lo presentan el 45,9% de los pacientes de la base de datos).

Curva ROC
El análisis de sensibilidad y especificidad del modelo, así como la curva ROC y su AUC, para este ejemplo, se pueden obtener con el siguiente código:

par(mfrow = c(1, 2))
library("Epi")
ROC(
  form = diag ~ edad + dep + sexo + tdolor, data = cleveland,
  plot = "sp"
)
ROC(
  form = diag ~ edad + dep + sexo + tdolor, data = cleveland,
  plot = "ROC", las = 1
)

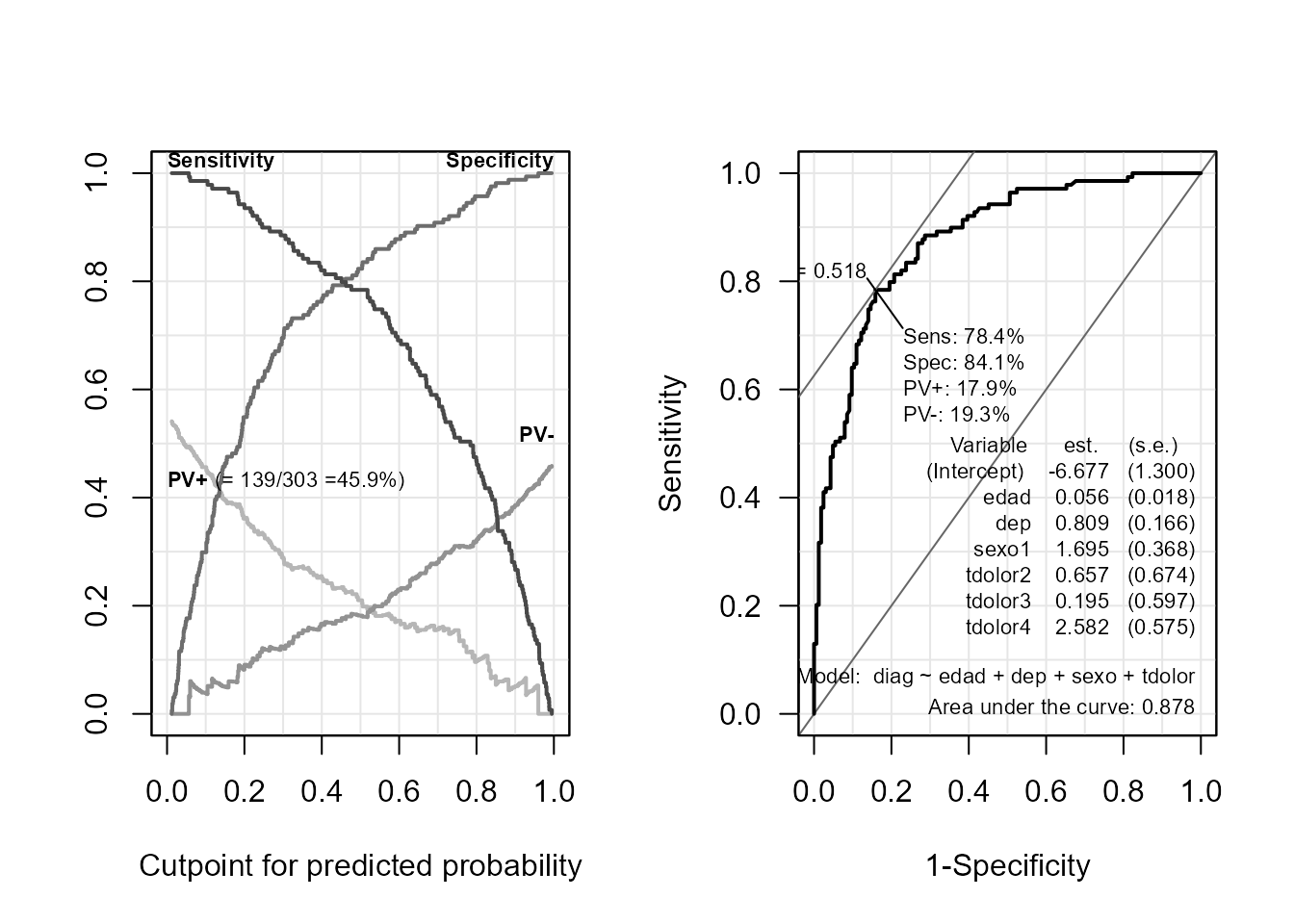
Figura 16.2: Gráfico de sensibilidad y especificidad según puntos de corte de discriminación (izquierda) y curva ROC (derecha) para el segundo modelo de regresión logística.

La Fig. 16.2 (izquierda) muestra que tomando como punto de corte una probabilidad cercana a 0,45 se obtienen valores de sensibilidad y especificidad alrededor de 0,8. No obstante, se deben evaluar los costes y riesgos de una mala clasificación (por ejemplo, dar tratamiento cuando no hace falta y no darlo cuando es necesario).

La Fig. 16.2 (derecha) representa la curva ROC de reg_log2. La curva está por encima de la diagonal, con lo que es mejor que un clasificador aleatorio. La AUC es de 0,878, con una sensibilidad de 78,4% y una especificidad de 84,1%. Si se realiza el análisis para reg_log se comprobará que la AUC es de 0,759, por lo que el segundo modelo es mejor para discriminar. Además, el gráfico también indica el valor del punto de corte óptimo, 0,518 (el que proporciona la mayor AUC, 0,878) junto con los correspondientes valores de sensibilidad, especificidad, etc. También muestra las estimaciones y los errores estándar (standar error, s.e.) de los coeficientes del modelo considerado.

16.6.2 Ejemplo de regresión de Poisson

A partir del mismo conjunto de datos, cleveland, ahora se considera como variable a explicar, variable respuesta, dhosp, el número de días de hospitalización de un paciente. Como variables explicativas se seleccionan las siguientes: diag, edad, sexo y tdolor, que son de distinto tipo, lo que permitirá ilustrar sus distintas interpretaciones.

Visualización ilustrativa

p1 <- ggplot(cleveland, aes(dhosp, fill = diag)) +
  geom_bar(position = "dodge")
p2 <- ggplot(cleveland, aes(x = factor(dhosp), y = edad)) +
  geom_boxplot()
library("patchwork")
p1 + p2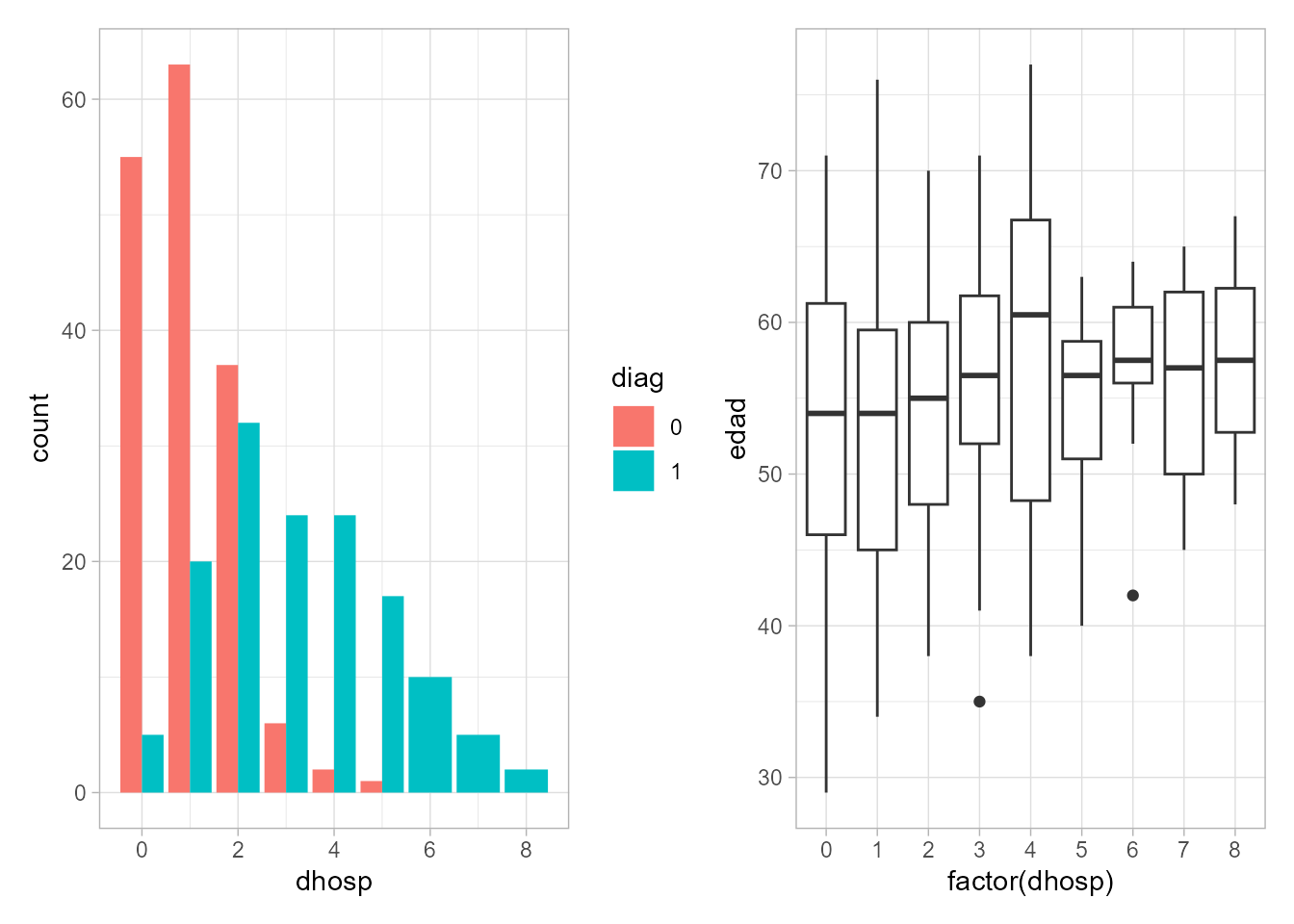

Figura 16.3: Gráfico de barras de \(dhosp\) según tipo de diagnóstico (izquierda) y gráficos de cajas de \(edad\) según el número de días de hospitalización (derecha).

A la vista de los gráficos de la Fig. 16.3, generados con las sentencias anteriores, diag parece ser una buena variable predictora del número de días de hospitalización, mientras que edad no tiene una influencia tan clara.

Ajuste e interpretación

reg_pois <- glm(dhosp ~ diag + edad + sexo + tdolor,
  data = cleveland, family = "poisson")

Al especificar family = "poisson", la función glm() selecciona automáticamente la función de enlace apropiada: el logaritmo (efectos multiplicativos).

summary(reg_pois)$coef
#>                  Estimate  Std. Error     z value     Pr(>|z|)
#> (Intercept) -0.2230728726 0.332125111 -0.67165314 5.018045e-01
#> diag1        1.0902902179 0.109731744  9.93595999 2.903654e-23
#> edad         0.0001026277 0.004877904  0.02103931 9.832143e-01
#> sexo1        0.2160286255 0.103297627  2.09132226 3.649919e-02
#> tdolor2      0.1408464230 0.205232539  0.68627725 4.925383e-01
#> tdolor3      0.1217757202 0.189404790  0.64293897 5.202637e-01
#> tdolor4      0.1215388103 0.178729482  0.68001546 4.964947e-01
exp(coef(reg_pois))[-1]
#>    diag1     edad    sexo1  tdolor2  tdolor3  tdolor4 
#> 2.975137 1.000103 1.241138 1.151248 1.129501 1.129233

De todas las variables introducidas en el modelo, solo diag y sexo son significativas (al 5%). Se confirma así lo visto en la Fig. 16.3 (derecha): que edad no influye en la respuesta. Al ser las dos variables significativas de tipo dicotómico, su interpretación, como en la regresión logística, se hace en función de la categoría de referencia, y ceteris paribus (esto en cualquier caso):

• El coeficiente de diag es 1,0903 pero se le debe aplicar la exponencial para tener como unidades de medida días. Así, el número medio de días de estancia en el hospital es 2,98 veces mayor con diag=1 que con diag=0 (categoría tomada como referencia).

• Algo similar se puede decir para sexo: un hombre (sexo=1) se espera que esté en el hospital, de media, 1,24 días por cada día que esté una mujer.

• De la misma manera se interpretarían los coeficientes asociados a tdolor, si bien no son significativos: cada uno de ellos expresaría la diferencia con los pacientes del grupo tdolor=1.

• Aunque el coeficiente asociado a edad tampoco es significativo, y su magnitud es ínfima, se da su interpretación, al ser la única variable continua: por cada año que aumenta la edad, el número medio de días en el hospital se ve multiplicado por 1,0001 (ínfimo).¹⁴¹

Para posteriores comparaciones, se considera otro modelo en el que se elimina tdolor (por no ser significativa):

reg_pois2 <- glm(dhosp ~ diag + sexo + edad,
  data = cleveland,   family = "poisson")

Adecuación
En los ajustes reg_pois y reg_pois2 hay información sobre la null y la residual deviance, con las que se puede realizar el contraste de comparación de modelos (el simple frente al elaborado) mencionado en la Sec. 16.4.2.

pchisq(reg_pois$deviance, reg_pois$df.residual, lower.tail = F)
#> [1] 0.1325654
pchisq(reg_pois2$deviance, reg_pois2$df.residual, lower.tail = F)
#> [1] 0.155157

Al ser los p–valores superiores a 0,05, se puede considerar que ambos modelos explican “mejor” que el modelo nulo, el que únicamente contiene la constante y el término aleatorio.

Predicción
Con los modelos ajustados, y comprobada su adecuación, se puede predecir valores, que en este caso son el número medio de días de hospitalización.

pacientes <- data.frame(
  diag = c("1", "1", "0", "0"),
  edad = c(50, 50, 50, 50),
  sexo = c("1", "0", "1", "0"),
  tdolor = c("4", "4", "4", "4"))
predict(reg_pois, pacientes, type = "response")
#>         1         2         3         4 
#> 3.3532035 2.7017171 1.1270752 0.9080983

Se han escogido, arbitrariamente, valores de las variables explicativas para 4 pacientes: los pacientes 1 y 2 presentan la enfermedad coronaria (diag=1) mientras que los pacientes 3 y 4 no; los pacientes 1 y 3 son hombres (sexo=1), mientras que el 2 y el 4 son mujeres; los cuatro tienen 50 años y son asintomáticos (tdolor=4). Las predicciones obtenidas indican que el paciente 1 (hombre con enfermedad coronaria) estará hospitalizado más días, de media, que el resto, aunque le sigue de cerca la paciente 2 (mujer con enfermedad coronaria).

También se pueden dibujar las predicciones modelo reg_pois de todo el conjunto de datos, que glm() ha guardado como fitted.values.

cleveland$hat <- reg_pois$fitted.values
g1 <- ggplot(cleveland, aes(x = edad, y = hat, colour = diag)) +
  geom_point() +
  labs(x = "Edad", y = "Días hospitalización")
cleveland$hat2 <- reg_pois2$fitted.values
g2 <- ggplot(cleveland, aes(x = edad, y = hat2, colour = diag)) +
  geom_point() +
  labs(x = "Edad", y = "Días hospitalización")
g1 + g2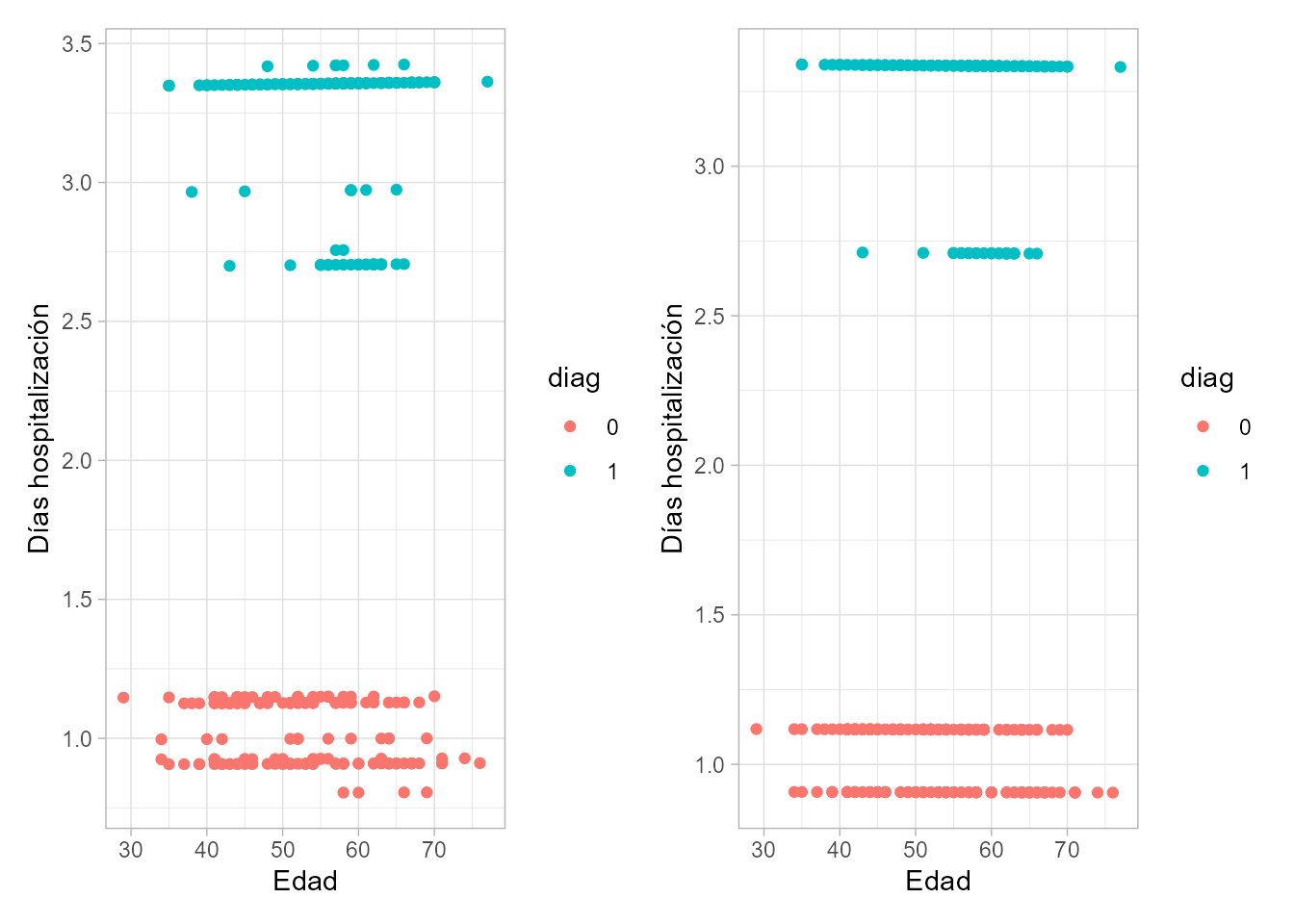

Figura 16.4: Predicciones de todo el conjunto de datos del modelo \(regpois\) (izquierda) y \(regpois2\) (derecha).

La Fig. 16.4 muestra las predicciones del número de días (promedio) de hospitalización para los 303 individuos considerados en el conjunto de datos y para cada uno de los dos modelos de regresión de Poisson considerados. Cabe recordar que en el primer modelo se consideran las variables diag, edad, sexo y tdolor, mientras que en el segundo se ha eliminado la variable tdolor. Lo primero que hay que destacar es que los puntos se “ordenan” en forma de líneas de puntos horizontales dispuestas verticalmente. Ello se debe a que (i) en el eje de abscisas figura la variable Edad, que no influye significativamente en los días de hospitalización (líneas horizontales); y (ii) las demás variables son categóricas, por lo que desplazan las líneas verticalmente, sin modificar su pendiente. El desplazamiento vertical diferenciado por colores, mediante la variable diag, es claro: la predicción del número de días (promedio) de hospitalización para personas con diag=1 es un valor en torno a 3, mientras que para aquellos con diag=0 es un valor en torno a 1. En ambos gráficos no se ha incluido identificación para la variable sexo, podría hacerse añadiendo apropiadamente facet_wrap(vars(sexo)), lo que permitiría ver que es el sexo el que genera las diferencias verticales (significativas, porque la variable sexo es significativa) de las dos líneas horizontales tanto en torno a hosp=3 como a hosp=1 (apreciables claramente en el gráfico de la derecha). Por último, como la diferencia entre el gráfico de la izquierda y el de la derecha es la inclusión o no de tdolor, queda claro que es dicha variable la que genera las distintas líneas horizontales de puntos (gráfico de la izquierda) con poca variabilidad vertical (por no ser significativa).

Resumen

En este capítulo se introduce el modelo de regresión lineal generalizado, indicado cuando las respuestas no son gaussianas (normales). En particular:

• Se introduce la función de enlace, que juega un papel importante en estos modelos.

• Se describen los casos particulares de regresión logística y de regresión de Poisson.

• Se muestra el uso de R para el ajuste de estos modelos.

• Se ilustra la interpretación de los coeficientes, tanto asociados a variables cuantitativas como a categóricas, y los demás resultados obtenidos con R, mediante casos prácticos.

• Se incluye el uso de la regresión logística como clasificador y se dan indicaciones al respecto mediante la curva ROC y la AUC.