Capítulo 53 Segmentación de clientes en el comercio minorista

Jaime Fierro Martín\(^{a}\), Rocío González Martínez\(^{a}\) y Cristina Sánchez Figueroa\(^{b}\)

\(^{a}\)Analyticae, SL
\(^{b}\)Universidad Nacional de Educación a Distancia

53.1 Motivación y conceptos clave

Los comercios minoristas (retailers) se mueven en un entorno turbulento y necesitan acercarse a sus clientes para asegurar su supervivencia. Su producto, o servicio, es nexo clave en el proceso de segmentación. En este contexto, conocer el perfil de los clientes permitirá detectar en qué momento de su ciclo de vida con la empresa se encuentran y desarrollar propuestas de valor que convengan en cada momento.

Segmentar se define como el proceso de dividir a los clientes, actuales o potenciales, en diferentes grupos o segmentos consistentes en individuos con características y niveles similares de interés (véase el Cap. 31 para una explicación detallada de las técnicas del clúster no jerárquico). Es un proceso creativo e iterativo con el fin de satisfacer con mayor acierto las necesidades de los clientes, proporcionando una ventaja competitiva y sostenible a la compañía. La segmentación viene dada por las necesidades de los clientes, no de la compañía, y debería ser revisada periódicamente.

Este caso práctico de negocio está basado en un proyecto real impulsado por el departamento de marketing de una empresa del sector retail que necesitaba mejorar el conocimiento de sus clientes, agrupándolos en función de su comportamiento de compra. Los resultados obtenidos fueron clave para definir la estrategia de marketing relacional de la compañía.

53.2 El modelo RFM tradicional

El modelo RFM (recency, frequency, monetary) es una técnica popular que se utiliza para analizar el comportamiento de compra de los clientes: cómo compran, su frecuencia de compra y cuánto gastan. Es un método útil para enriquecer la segmentación de los clientes en varios grupos que permitan la personalización e identificación de aquellos clientes más proclives a responder a las promociones. El análisis RFM depende de las medidas de actualidad (recency) (R), frecuencia (frequency) (F) y valor monetario (monetary) (M), que son tres importantes variables relacionadas con la compra que influyen en las posibilidades de compra futura de los clientes.

El modelo RFM tradicional categoriza el valor de las variables dividiéndolas en quintiles, a partir de los cuales se calcula una puntuación única que representa el valor del cliente. Sin embargo, no es muy preciso. Si el intervalo de frecuencia de compras se fija entre 0 y 20, en términos de negocio podría interpretarse como que un cliente con una sola compra será igual que otro que tenga 20. Por ello, los enfoques de conjuntos clásicos pueden resultar poco funcionales (Martı́nez et al., 2019). En este caso práctico, se propone una mejora en la definición de los intervalos mediante la aplicación del ranking de percentiles. Este método, que se ha denominado modelo RFM extendido, proporciona un procedimiento robusto para tratar los valores atípicos (outliers) y además normaliza las variables entre 0 y 1 para evitar las diferencias de peso entre las variables, permitiendo así la correcta implementación del algoritmo de segmentación.

53.3 El modelo RFM extendido

Los autores de este caso práctico recomiendan seguir una metodología de gestión de proyectos. La metodología CRISP-DM (Chapman et al., 2000), presentada en el Cap. 2, es un estándar ampliamente utilizado en los proyectos de ciencia de datos.

Una vez definido el problema (mejorar el conocimiento que una empresa de comercio minorista tiene de sus clientes, agrupándolos en función de su comportamiento de compra), la recopilación y comprensión de los datos (primera etapa del modelo CRISP-DM) se establece como etapa esencial para el desarrollo del proyecto.

53.3.1 Recopilación y comprensión de los datos

Hoy en día, la mayoría de las empresas de e-commerce y comercio minorista tradicional cuentan con sistemas que permiten registrar los datos básicos de cada una de sus ventas (fecha, artículo, cantidad e importe) asociados a un código único de cliente. La información contenida en estos datos de compra atesora gran valor, ya que carecen del sesgo y subjetividad propios de otras informaciones obtenidas mediante encuestas de opinión, estudios de mercado, entrevistas y grupos de discusión, etc. Estos datos suelen encontrarse en las plataformas ERP (Enterprise Resource Planning) de gestión de pedidos y ventas o CRM (Customer Relationship Management) de las empresas.

El lector es, o será, consciente de que la fase de extracción, carga y limpieza de los datos es la más exigente del proyecto, y donde se empleará gran parte de los recursos y tiempo de todo el proyecto. R cuenta con gran cantidad de paquetes y recursos que facilitan la extracción desde diferentes tipos de bases de datos.

Para este caso práctico serán necesarias las siguientes librerías:

library("tidyverse")
library("lubridate")
library("factoextra")
library("ggpubr")
library("CDR")
data("datos_retail")

Cualquier tipo de estudio o proyecto de ciencia de datos requiere familiarizarse con los datos y determinar si presentan suficiente exactitud, completitud, consistencia, credibilidad y actualidad (Muñoz-Reja et al., 2018). Los datos de transacciones de venta registrados por las empresas pueden contener valores perdidos, inexactos, outliers, etc. Para determinar la acción a tomar, o no, de limpieza o corrección de los datos de partida, es esencial conocer el negocio y las consecuencias que estas operaciones tendrán en el resultado final de la segmentación.

El conjunto de datos de muestra contiene 200.000 observaciones correspondientes a transacciones de compra. Las siguientes variables iniciales están explicadas en el set de datos:

head(datos_retail)
#> # A tibble: 6 x 4
#> id_ticket fecha importe_venta codigo_socio
#> <chr> <date> <dbl> <chr>
#> 1 num_1646673 2021-10-30 12.4 id_1076134
#> 2 num_2762559 2021-12-03 38.8 id_0552641
#> 3 num_0309422 2022-01-07 67.8 id_0537369

53.3.2 Cálculo de las variables del modelo RFM

Identificadas las variables iniciales, es necesario calcular los factores clave del modelo RFM:

• La variable actualidad, recency (R), es el intervalo de tiempo transcurrido desde la última compra de un cliente hasta la fecha de elaboración del modelo RFM.

• La variable frecuencia, frequency (F), se obtiene agrupando las compras por cliente y contando el número total de tickets únicos.

• La variable valor monetario, monetary (M), se calcula sumando todos los importes de venta por cliente.

fecha_estudio_rfm <- ymd("2022-08-01")

rfm <- datos_retail |>
  group_by(codigo_socio) |>
  summarise(
    frecuencia = n_distinct(id_ticket),
    monetario = sum(importe_venta, na.rm = TRUE),
    fecha_transaccion_reciente = first(fecha, order_by = desc(fecha))
  ) |>
  mutate(actualidad = time_length(interval(start = fecha_transaccion_reciente, end = fecha_estudio_rfm), unit = "days"), .keep = "unused")

head(rfm) # el lector puede ver las variables del Modelo RFM

53.3.3 Breve análisis exploratorio de las variables del modelo RFM

Del análisis puede concluirse que:

• 107.929 clientes han realizado una media de 1,85 compras, con un importe medio total de 70,56€ y 450,4 días de media desde la última compra hasta la fecha de realización del estudio, con una fuerte asimetría positiva de los valores frequency y monetary (véase Fig. 53.1).

• Se detecta una gran estacionalidad de las compras, como se puede apreciar en la agrupación de las observaciones de recency. Teniendo en cuenta la fecha en la que se realiza el análisis, los valores obtenidos en la variable recency se pueden interpretar como el período de ventas de la campaña navideña.

set.seed(12345)
plot_data <- rfm |>
  slice_sample(n = 2000) |>
  pivot_longer(!codigo_socio, names_to = "variable", values_to = "valor")
plot_data |>
  ggplot(aes(x = variable, y = valor)) +
  geom_boxplot(outlier.shape = NA, color = "red") +
  geom_jitter(alpha = 1 / 10) +
  facet_wrap(~variable, ncol = 6, scales = "free") +
  theme(strip.text.x = element_blank(), text = element_text(size = 9))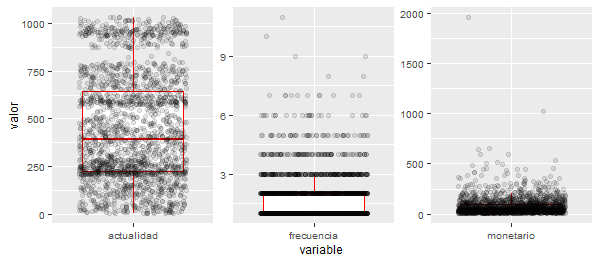

Figura 53.1: \(Box\)-\(plot\) de las variables RFM.

53.3.4 Cálculo del ranking de percentiles

Los valores de ranking son relativos entre clientes y no pueden ser utilizados para objetivos de negocio, basados en valores absolutos de puntuación por cliente.

rfm_rank <- rfm |>
  mutate(across(.cols = c("frecuencia", "monetario"), percent_rank, .names = "rank_{.col}")) |>
  mutate(across(.cols = c("actualidad"), ~ percent_rank(-.x), .names = "rank_{.col}")) # menor recency indica mayor puntuación en rank

Se podría decir que el análisis RFM combina tres atributos clave de los clientes para construir un ranking que permite agruparlos de forma útil para el negocio. Así, a un cliente que compró en una fecha reciente (recency) se le otorgan más puntos. Si compró muchas veces (frecuency), también se le coloca más arriba en el ranking. Finalmente, si gastó más en el total de sus compras (Monetary), también se le puntúa más alto. Combinando estas tres puntuaciones se obtiene un ranking RFM. Para la elaboración de este ranking se parte del concepto de percentil. La idea es asignar a cada cliente una puntuación según las tres variables o factores clave del modelo RFM, de modo que los mejores clientes serán los que tengan una puntuación mayor.

head(rfm_rank) # el lector puede ver la puntuación del ranking

Una vez que se tienen los rankings de percentiles en las tres variables para todos los clientes, se procede a su clusterización mediante el método k-means.

53.3.5 Modelado: RFM mediante k-means

El modelo establecido debe proporcionar una segmentación de clientes con sentido de negocio. En este caso práctico se opta por el algoritmo de clustering estándar que presenta la ventaja de que es muy intuitivo y permite trabajar con grandes conjuntos de datos. Como el lector ha podido comprobar en la Parte VI de este manual, existen otros muchos algoritmos de aprendizaje no supervisado que pueden ser empleados.

El número óptimo de clústeres (o segmentos, en la jerga del marketing) es uno de los retos a la hora de aplicar técnicas de clustering. No existe una manera exclusiva de encontrar el número adecuado de clústeres. Se trata de un proceso subjetivo que depende de los datos, del tipo de clustering empleado y, en este caso, de que el número elegido tenga sentido y utilidad en el negocio. Existen numerosos métodos para facilitar la elección del número de clústeres; entre ellos destacan el Elbow method, el Average silhouette method y el Gap statistic method (véase Cap. 31), que se pueden calcular con la función fviz_nbclust() del paquete factoextra para realizar una buena elección.

Con el método Elbow, el número óptimo de clústeres se calcula como sigue:

set.seed(123)
muestra_clusters <- rfm_rank |>
  slice_sample(n = 5000) |>
  select(matches("rank"))

fviz_nbclust(x = muestra_clusters, FUNcluster = kmeans, method = "wss", k.max = 10)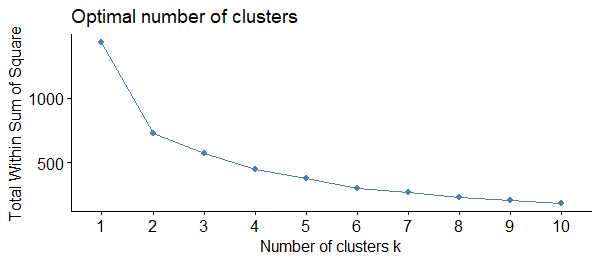

Figura 53.2: Número óptimo de clústeres (método Elbow).

En la Fig. 53.2 se observa que la varianza total intraclúster apenas mejora a partir del cuarto clúster.

El algoritmo de clustering k-means se entrena con las variables RFM normalizadas con el ranking. La salida de la función kmeans() del paquete base stats es un objeto que, entre otros componentes, ofrece un vector numérico indicativo del clúster al que pertenece cada uno de los clientes.

set.seed(123)
km_fit <- kmeans(x = rfm_rank[, 5:7], centers = 4, nstart = 10)

clientes_segmentos <- rfm_rank |>
  mutate(segmento = km_fit$cluster)

head(clientes_segmentos) # el lector puede ver el segmento al que pertence el cliente

53.3.6 Descriptivos e interpretación de los segmentos

Los segmentos obtenidos deben tener sentido y utilidad de negocio. Para ello es imprescindible proporcionar los estadísticos descriptivos de cada segmento y proceder a su interpretación de perfil de cliente.

descriptivo_segmentos <- clientes_segmentos |>
  group_by(segmento) |>
  summarise(across(c("monetario", "frecuencia", "actualidad"),
    .fns = mean, .names = "md_{.col}" ), n_clientes = n()) |>
  ungroup() |>
  relocate(segmento, n_clientes)

head(descriptivo_segmentos)
#> # A tibble: 4 x 5
#> segmento n_clientes md_monetario md_frecuencia md_actualidad
#> <int> <int> <dbl> <dbl> <dbl>
#> 1 1 23551 36.2 1.07 239.
#> 2 2 23632 77.0 2.26 567.
#> 3 3 28809 128. 3.11 188.
#> 4 4 31937 39.3 1.00 757.

Interpretación de los segmentos:

• 1-Nuevos probando: segmento que agrupa nuevos clientes que están realizando compras desde hace poco tiempo y tienen un gran potencial de desarrollo. Es un segmento de clientes con interés para la empresa.
• 2-No podemos perder: se trata de aquellos churn³⁰² que fueron buenos clientes en términos monetarios y de frecuencia, pero que hace tiempo que no realizan nuevas compras. La compañía debe hacer un esfuerzo en recuperar estos clientes para convertirlos al segmento TOP.
• 3-Top: reúne a los mejores clientes de la empresa. Son clientes que compran con frecuencia, están activos y aportan ventas a la compañía. Es el segmento de clientes con mayor interés para la empresa.
• 4-Una compra: segmento formado por aquellos clientes que han realizado una única compra hace tiempo. Presentan frecuencia, actualidad y valor monetario bajo. Se trata de un segmento de clientes con escaso interés para la compañía.

segmentos_descriptivo <- clientes_segmentos |>
  mutate(segmento = case_when(
    segmento == 1 ~ "1_Nuevos probando",
    segmento == 2 ~ "2_No perder",
    segmento == 3 ~ "3_Top",
    segmento == 4 ~ "4_Una compra")) |>
  group_by(segmento) |>
  summarise(across( .cols = where(is.numeric), .fns = mean),
            n_clientes = n()) |>
  ungroup() |>
  relocate(segmento, n_clientes)

table_dot_plot <- segmentos_descriptivo |>
  pivot_longer(cols = c("rank_monetario", "rank_frecuencia", "rank_actualidad"), names_to = "Variable RFM", values_to = "Puntuación")

ggdotchart(table_dot_plot, x = "Variable RFM", y = "Puntuación",
  group = "segmento", color = "segmento", palette = "jco",
  add = "segment", position = position_dodge(0.3),
  sorting = "none", facet.by = "segmento", dot.size = 5,
  rotate = TRUE, legend = "none")

La Fig 53.3 muestra cada uno de los segmentos indicados. El ranking obtenido ayuda a identificar las diferencias en los tipos de clientes y es útil para decidir a qué segmentos enfocarse y qué estrategias usar para cada uno.

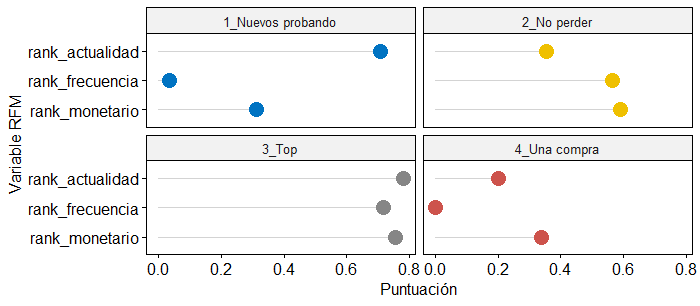
Figura 53.3: \(Lollipop\) de variables RFM.

53.3.7 Puesta en producción

Calculado el modelo RFM k-means, la compañía puede incorporar periódicamente los datos de los clientes nuevos o actualizarlos. De este modo, los segmentos de clientes se actualizarán y, más allá de las acciones de marketing mix que realicen las compañías gracias a la segmentación, podrán analizarse las migraciones de clientes entre los diferentes segmentos en el período estudiado. La función cl_predict() facilita la actualización periódica de los segmentos con el modelo entrenado.