Capítulo 58 Predicción de consumo eléctrico con redes neuronales artificiales
Jose Manuel Sanz Candales
Red Eléctrica de España
58.1 Introducción
Red Eléctrica, como operador del sistema eléctrico español, tiene como misión principal garantizar la continuidad del suministro eléctrico en España. Para ello, entre otras muchas tareas, se desarrollan, evolucionan y mantienen algoritmos de previsión del consumo eléctrico y de la producción con las principales energías renovables (eólica y solar) para distintas frecuencias (horas, días, meses, años, etc.) y escalas temporales (anual, horaria, quinceminutal).
Este caso de uso se sitúa en el departamento de Ciencia de Datos del Operador del Sistema. Es el principio del año 2018 y el área de planificación de la empresa solicita una predicción del consumo eléctrico en España, medida en MWh, para el año actual y el siguiente (2018 y 2019). La predicción se llevará a cabo con una red neuronal artificial (RNA, véase Cap. 36) y es importante destacar que este desarrollo no está previsto en el presupuesto del año, por lo que tanto el software como los datos de entrada deben ser, en la medida de lo posible, gratuitos.
58.2 Datos de entrada
Respecto a los datos de entrada de la RNA, se requiere tanto una serie histórica de la variable a predecir (el consumo eléctrico) como de las variables que se seleccionen para explicar adecuadamente su comportamiento.
En cuanto a la serie histórica de consumo eléctrico anual, Red Eléctrica, en su web corporativa, publica datos estadísticos accesibles de forma abierta. Sin embargo, el histórico publicado comienza en 2012 y sería conveniente tener un período de tiempo más amplio para poder entrenar adecuadamente las RNA candidatas a ser utilizadas. Se realiza una búsqueda de otras fuentes y, afortunadamente, se encuentra que el Instituto para la Diversificación y Ahorro de la Energía (IDAE) publica datos desde 1990, con agregación anual, del consumo final de energía eléctrica en miles de toneladas equivalentes de petróleo –ktep–.
Como los datos se deben entregar en MWh, la predicción resultante se tendrá que convertir con el coeficiente que indican en la web del IDAE (1 MWh = 0,086 tep).
En cuanto a la elección de las features o variables explicativas, se sabe que, históricamente, las variaciones interanuales del consumo eléctrico dependen del comportamiento de la economía de una forma directa: si la economía crece, también crece el consumo eléctrico. Como indicador del comportamiento de la economía se decide tomar el PIB per cápita, que se puede encontrar en el siguiente enlace, disponible de forma pública en Expansión - datos macro: https://datosmacro.expansion.com/pib/espana. Además del PIB per cápita, se utilizarán otras dos variables explicativas: una relacionada con el mercado inmobiliario y otra relacionada con el empleo. Dado que no son públicas, están anonimizadas; también están escaladas entre 0 y 1 (dividiendo todos los valores de cada variable entre el mayor de su serie). Dado que se dispone de datos de estas dos variables desde el año 2000, el conjunto de datos comienza en este año.
Una vez definido el conjunto de datos que se utiliza para determinar la RNA que mejor prediga el consumo eléctrico en España en los años 2018 y 2019, que como se verá a continuación es un conjunto de datos muy pequeño y sencillo, se puede comenzar a modelar la RNA en R.
58.3 Modelización
En el siguiente fragmento de código (chunk) se lee el conjunto de datos, consumoelectricoanual_2, del paquete CDR, se convierte el formato data.table al formato data.frame y se visualizan sus primeras 3 filas:
library("CDR")
df <- CDR::consumoelectricoanual_2
class(df) <- class(as.data.frame(df))
head(df, 3)
#> Año PIB Consumo Inmob Empleo
#> 1 2000 15.97 16.205 0.7525093 0.6561190
#> 2 2001 17.20 17.279 0.7687356 0.6832698
#> 3 2002 18.09 17.671 0.7836143 0.7104178En este caso de uso ya se dispone de los datos reales de 2018 y 2019 (lo que permitirá validar la precisión del modelo), pero en un caso real, a principios de 2018 el PIB per cápita de 2018 y 2019 será una predicción. Lógicamente, el consumo eléctrico anual también será desconocido, siendo, precisamente, el objeto de la predicción. Es decir, se supone que los datos de consumo eléctrico de 2018 y 2019 no existen y, en consecuencia, no se pueden utilizar ni para entrenar ni para evaluar la precisión del modelo (para ello habrá que utilizar datos anteriores a 2018).
La siguiente chunk proporciona la matriz de varianzas-covarianzas de las variables PIB per cápita, Consumo, Inmob, Empleo:
cormat <- round(cor(df[c("PIB", "Consumo", "Inmob", "Empleo")]), 2)
head(cormat)
#> PIB Consumo Inmob Empleo
#> PIB 1.00 0.81 0.90 0.93
#> Consumo 0.81 1.00 0.64 0.71
#> Inmob 0.90 0.64 1.00 0.99
#> Empleo 0.93 0.71 0.99 1.00Como se puede observar en la matriz anterior, la correlación entre la variable a predecir y las distintas variables explicativas es fuerte y positiva (es decir, cuando crece una también crece la otra). Si, además, se visualiza la gráfica entre PIB y consumo en el tiempo (Fig. 58.1), se aprecia de forma aún más clara esta intensa correlación:
library("ggplot2")
library("reshape2")
df_m <- melt(df[c("Año","PIB","Consumo")], id.vars = "Año")
df_m_plot <- df
colnames(df_m_plot) <- c('Año','PIB per cápita (k€/año)',
'Consumo eléctrico anual (ktep)')
df_m_plot_melt <- melt(df_m_plot[c("Año","PIB per cápita (k€/año)",
"Consumo eléctrico anual (ktep)")], id.vars = "Año")
options(repr.plot.width = 15, repr.plot.height = 8)
ggplot(df_m_plot_melt, aes(Año, value, col = variable)) +
geom_line(size = 2.5)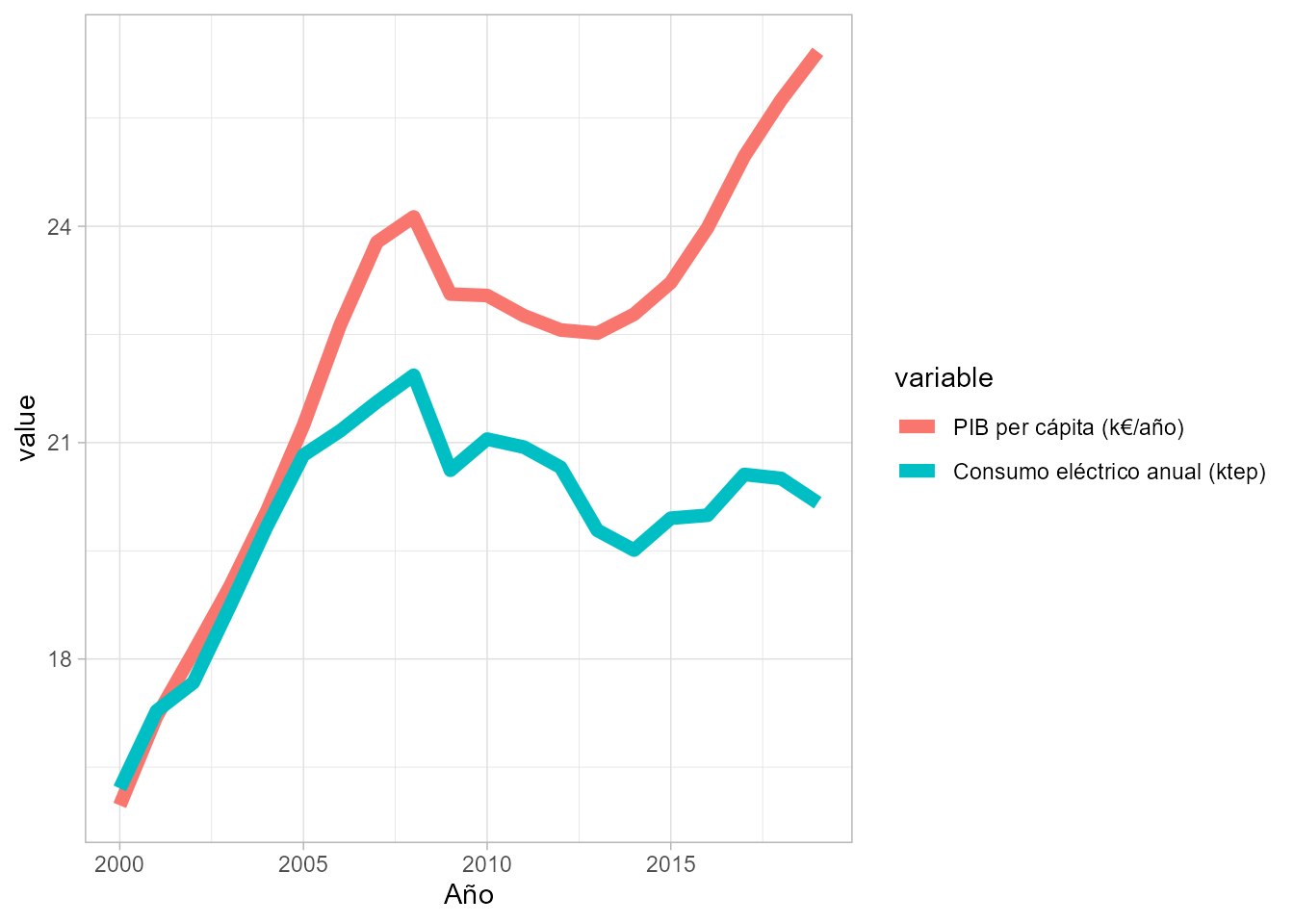
Figura 58.1: Evolución del PIB y el consumo eléctrico en España.
En la Fig. 58.1 se observa que hasta 2005 las curvas que representan la evolución temporal de ambas variables están prácticamente superpuestas, pero desde 2006 las líneas se separan. ¿A qué puede deberse? Uno de los principales motivos probablemente sea las medidas de eficiencia energética que se han ido introduciendo en los últimos lustros (iluminación led, electrodomésticos, dispositivos con menor consumo, etc.).
Una vez se han explorado los datos (en este caso la exploración ha sido muy breve, pero es muy habitual en proyectos reales que la exploración y limpieza de los datos requiera en torno al 80% del tiempo), se procede a dividir el conjunto de datos (desde 2000 hasta 2017, ya que 2018 y 2019 son los años en los que se pretende predecir) en dos partes:
- subconjunto de entrenamiento y validación (90% de las filas);
- subconjunto de test (10% restante).
Previamente, se debe escalar también la variable PIB per cápita para que sus valores varíen entre 0 y 1 (las otras dos variables explicativas ya venían escaladas en la fuente de la cual se tomaron) y que la RNA funcione de forma correcta:310
# estandarizar la variable explicativa "PIB" entre 0 y 1
df$PIB = df$PIB/max(df$PIB)
set.seed(123)
df_aux <- df[df$Año < 2018, ]
n <- nrow(df_aux)
trainIndex <- sample(1:n, size = round(0.85 * n), replace = FALSE)
df_train <- df_aux[trainIndex, ]
df_test <- df_aux[-trainIndex, ]
df_testEl siguiente paso sería modelizar los datos con distintos modelos de machine learning y comparar sus resultados para determinar cuál es el más preciso para este conjunto de datos. En este ejemplo, por simplicidad no se incluye este proceso de prueba y comparación entre distintos modelos, que en el caso de uso real da lugar a elegir una red neuronal simple o perceptrón multicapa (véase Cap. 36), también conocido por su acrónimo en inglés MLP (multi layer perceptron).
Para elegir el valor de los hiperparámetros que faciliten el mejor resultado (en este caso el número de capas ocultas y el número de neuronas en cada una de estas capas) se utilizan las dos siguientes técnicas: \((i)\) grid search (para probar distintas combinaciones de hiperparámetros) y \((ii)\) cross-validation (para entrenar y validar aprovechando todos los registros del conjunto de entrenamiento-validación).
En este caso de uso, se realizan distintas pruebas combinando el número de neuronas de cada capa oculta. En concreto, en la primera y la segunda capa oculta se deja un número constante de neuronas (5), y en la tercera se prueba con 4 y 5 neuronas. Es decir, se entrenará un modelo con tres capas ocultas y con 5 neuronas en cada capa oculta y otro con 5 neuronas en las dos primeras capas y 4 neuronas en la tercera.
En la siguiente chunk se importan los paquetes necesarios, neuralnet y caret, se construye la estructura de la red en la variable grid y se define el número de folds (en cuántas partes se divide en conjunto de entrenamiento para entrenar y validar con todos los datos del conjunto) de la validación cruzada (véase Cap. 10, Sec. 10.4). Por último, se entrena el modelo.
El proceso está muy simplificado para que sea fácil de entender. No obstante, lo habitual en la práctica es probar más opciones de grid search y hacer una división mayor del conjunto de datos para cross-validation (es bastante habitual entre 5 y 10 partes):
# lee paquetes
library("neuralnet")
library("caret")
# define la estructura de la red
grid <- expand.grid(layer1 = c(5), layer2 = c(5), layer3 = c(4,5))
# establece semilla para que los resultados del entrenamiento sean siempre los mismos
set.seed(123)
# define el número de folds en validación cruzada
train_control <- trainControl(method = "cv",
number = 2,
verbose = TRUE)
# entrenar el modelo
model <- train(Consumo ~ PIB+Inmob+Empleo,
data = df_train,
trControl = train_control,
method = "neuralnet",
tuneGrid = grid)Para mostrar los resultados se aplica la función print sobre la variable model, cuya salida es el texto comentado debajo de la línea de print.
print(model)
#> Neural Network
#>
#> 15 samples
#> 3 predictor
#>
#> No pre-processing
#> Resampling: Cross-Validated (2 fold)
#> Summary of sample sizes: 8, 7
#> Resampling results across tuning parameters:
#>
#> layer3 RMSE Rsquared MAE
#> 4 0.9713547 0.7631649 0.8521702
#> 5 0.9452518 0.72532010.8165410
#>
#> Tuning parameter 'layer1' was held constant at a value of 5
#> Tuning parameter 'layer2' was held constant at a value of 5
#> RMSE was used to select the optimal model using the smallest value.
#> The final values used for the model were layer1 = 5, layer2 = 5 and layer3 = 5.La RNA con mejor resultado (menor error en el conjunto de entrenamiento / validación) es la que tiene 3 capas con 5 neuronas cada una. Con esta arquitectura de red se predice el consumo eléctrico para el conjunto de datos que se habían reservado para test (años 2006, 2007 y 2017), para comprobar que el modelo generaliza bien (es decir, para datos nuevos los resultados de las predicciones tienen un error del orden de los que resultan del entrenamiento del modelo). Para ello, se calcula una métrica de error, por ejemplo, el mean absolute error (MAE) de las predicciones para dicho conjunto de test:
df_test[c("Año", "Consumo")]
#> Año Consumo
#> 7 2006 21.163
#> 8 2007 21.564
#> 18 2017 20.559
predict(model, df_test)
#> 7 8 18
#> 21.50816 21.83445 20.12596
MAE_test = (abs(21.163-21.50816)+abs(21.564-21.83445)+abs(20.559-20.12596))/3
MAE_test
#> [1] 0.34955El modelo seleccionado ya está listo para predecir el consumo eléctrico anual en 2018 y 2019, el encargo del área de planificación de la empresa. Para ello, simplemente se utiliza la función predict() del modelo. Previamente, se añade una columna en el conjunto de datos original df que contendrá los valores predichos, para más adelante comprobar gráficamente el valor predicho frente al real que, en este caso ficticio, ya es conocido:
df["Prediccion_MLP"] <- NAA continuación, se hace la predicción del año 2018 y se añade el resultado a esta nueva columna del conjunto de datos:
df_pred_2018 <- df[df$Año == 2018, ]
df$Prediccion_MLP[df$Año == 2018] <- predict(model,
df_pred_2018[c("PIB","Inmob","Empleo")])Se hace también la predicción para el año 2019 y se visualizan las predicciones añadidas al conjunto de datos para ambos años:
df_pred_2019 <- df[df$Año == 2019, ]
df$Prediccion_MLP[df$Año == 2019] <- predict(model, df_pred_2019[c("PIB","Inmob","Empleo")])
tail(df, 3)
#> Año PIBConsumo Inmob Empleo Prediccion_MLP
#> 18 2017 0.9451173 20.559 0.9907827 0.9816742 NA
#> 19 2018 0.9746404 20.504 0.9939372 0.9913677 20.22787
#> 20 2019 1.0000000 20.166 1.0000000 1.0000000 20.16409Estos son los datos que se entregarían como resultado de la petición de información (convertidos a MWh aplicando el coeficiente que se mencionó en la Sec. 58.2).
Claro está, en el momento en que se entregan las predicciones para 2018 y 2019 todavía no se sabe cuál es su precisión, pero a principios de 2020 ya es posible calcular la bondad del modelo seleccionado, y es lo que se hace en las siguientes chunks:
df_m_mlp <- melt(df[c("Año","Consumo","Prediccion_MLP")], id.vars = "Año")
df_mlp_plot <- df
colnames(df_mlp_plot) <- c('Año','PIB','Consumo eléctrico anual real',
'Inmob','Empleo','Prediccion MLP Consumo eléctrico anual')
df_m_mlp_plot <- melt(df_mlp_plot[c("Año","Consumo eléctrico anual real",
"Prediccion MLP Consumo eléctrico anual")], id.vars = "Año")
ggplot(df_m_mlp_plot, aes(Año, value, col = variable)) +
geom_point(size = 2) +
geom_line()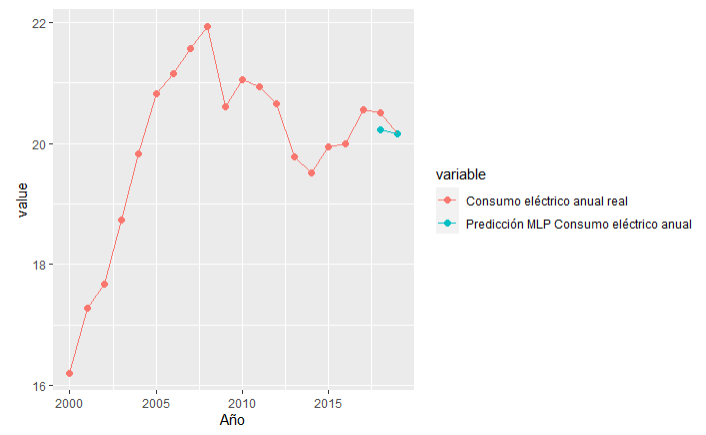
Figura 58.2: Consumo eléctrico real y predicho en España: 2018 y 2019.
En la Fig. 58.2, se puede comprobar que las predicciones (puntos azules) son bastante buenas, con unos errores del orden de los que se habían obtenido en el conjunto de test, por lo que parece que no hay sobreentrenamiento.