Capítulo 29 \(\bf \textit{Boosting}\) y el algoritmo XGBoost

Ramón A. Carrasco\(^{a}\), Itzcóatl Bueno\(^{a,\hspace{0,05cm}b}\) y José-María Montero\(^{c}\)

\(^{a}\)Universidad Complutense de Madrid
\(^{b}\)Instituto Nacional de Estadística
\(^{c}\)Universidad de Castilla-La Mancha

29.1 Métodos ensamblados: bagging vs. boosting

Boosting es el segundo de los paradigmas de aprendizaje ensamblado introducido en el Cap. 28. La principal diferencia con el primero de ellos, bagging, radica en cómo se combinan los modelos individuales (también denominados “débiles”) para obtener una predicción final. Para diferenciar uno de otro de una forma intuitiva, si se quisiera organizar una fiesta y se tuviese que tomar una decisión sobre la la decoración, el bagging pediría opinión a distintos amigos al mismo tiempo. Después se combinarán todas sus ideas para tomar una decisión final sobre la decoración de la fiesta (la unión hace la fuerza). Sin embargo, el boosting pediría opinión a un amigo en particular. Si su respuesta no es convincente, entonces buscaría la ayuda de otro amigo, quien trataría de mejorar la respuesta anterior. Este proceso continuaría secuencialmente, solicitando la ayuda de diferentes amigos y construyendo sobre las respuestas anteriores para obtener una decisión final más precisa y refinada sobre la decoración de la fiesta.

29.2 ¿Qué es el boosting?

Como se a avanzado en la sección anterior, el boosting (Schapire & Freund, 2012) es, junto con el bagging, el paradigma de aprendizaje ensamblado más popular. Como el bagging, el boosting agrega múltiples modelos con menor precisión (débiles) combinando sus predicciones para obtener un metamodelo con un porcentaje de clasificación correcta más alto. Los árboles de decisión son los modelos base o débiles que se usan más frecuentemente. En este caso, para llegar al metamodelo a partir de los modelos base, es necesario introducir ponderaciones a los árboles basándose en las clasificaciones erróneas del árbol previamente entrenado.

Continuando con las diferencias entre ambos paradigmas, en cuanto al objetivo, el principal objetivo intrínseco de los algoritmos de bagging es el de la reducción de la varianza, mientras que el de los algoritmos de boosting es la reducción del sesgo.

Otra diferencia entre ambos paradigmas, como se deduce de la introducción intuitiva anteriormente expuesta, es que en el bagging los algoritmos simples se usan en paralelo para aprovecharse entre ellos, ya que el error se puede reducir significativamente al promediar las salidas de los modelos simples. En términos coloquiales, es como si a la hora de dar solución a un problema y preguntar a varias personas, independientes entre sí, se adopta la solución mayoritaria. El boosting utiliza los modelos simples de forma secuencial, sacando ventaja de la dependencia entre dichos modelos simples. El rendimiento del modelo global o metamodelo mejora haciendo que un modelo simple posterior le dé más importancia a los errores cometidos por un modelo simple anterior. Volviendo al símil de la resolución de un problema, es como si se aprovechase el conocimiento de los errores de otros para mejorar no cometiéndolos posteriormente.

Finalmente, aunque hay más, en el boosting las predicciones de cada modelo simple se combinan por medio de una votación “ponderada” (para problemas de clasificación) o de una suma ponderada (para problemas de regresión) para producir la predicción final. Ello se debe a que, a diferencia del bagging, los modelos simples no se entrenan de forma independiente, sino que se ponderan según los errores de los anteriores.

Además de la reducción del sesgo, uno de los mayores problemas del machine learning, el boosting tiene las siguientes ventajas:

Su sencilla implementación mediante algoritmos fáciles de comprender e interpretar que aprenden de sus propios errores.
No requieren preprocesamiento de los datos y tienen rutinas que tratan la cuestión de los datos faltantess.
Tiene una alta eficacia computacional ya que, al tener la precisión predictiva como prioridad principal en la fase de entrenamiento, pues selecciona las variables que aumentan su poder predictivo, reduce la dimensión del problema.

En cuanto a las desventajas, merece la pena destacar las siguientes:

Mientras que en el bagging (por ejemplo, en el random forest) agregar más árboles al random forest ayuda a estabilizar el error sin provocar un sobreajuste del modelo, en el boosting sí puede dar lugar a sobreajuste y, por ello, hay que ser cauteloso a la hora de agregar nuevos árboles.
Como el boosting aprende iterativamente de los errores en árboles anteriores, puede llevar a sobreajustar el modelo. Aunque este enfoque produce predicciones más precisas, muchas veces mejores que la mayoría de algoritmos, puede llevar a ajustar las observaciones atípicas. Esta es una desventaja respecto del bagging y por ello esta última es preferible cuando se trabaja con conjuntos de datos muy complejos con un gran número de observaciones atípicas.
Otra desventaja del boosting es que su tiempo de procesamiento es muy elevado, puesto que su entrenamiento sigue una lógica secuencial. En el proceso de entrenamiento, un árbol debe esperar a que el inmediatamente anterior sea entrenado para iniciar su entrenamiento, y esto limita la escalabilidad del modelo. Mientras tanto, el bagging entrena los árboles en paralelo, lo que hace que su tiempo de procesamiento sea más rápido. Por tanto, el boosting tiene más eficacia computacional que el bagging (solo utiliza variables “importantes”), pero es menos eficaz respecto al número de recursos utilizados.
Finalmente, igual que el bagging, los algoritmos de boosting presentan el inconveniente de la dificultad de interpretación que tienen respecto a los árboles de decisión. En este sentido, ambos algoritmos de ensamblado se pueden considerar como “de caja negra”.

29.3 \(\bf \textit{Gradient boosting}\)

Uno de los algoritmos de boosting más conocidos es el gradient boosting (GB).²⁰⁰ Mientras que el random forest} selecciona combinaciones aleatorias de variables en cada proceso de construcción de un árbol, el gradient boosting selecciona las variables que mejoran la precisión con cada nuevo árbol. Por lo tanto, la construcción del modelo es secuencial, puesto que cada nuevo árbol se construye utilizando información derivada del árbol anterior y, en consecuencia, la construcción de estos árboles no es independiente. En cada iteración se registran los errores cometidos en los datos de entrenamiento y se tienen en cuenta para la siguiente ronda de entrenamiento. Además, se ponderan las observaciones (o instancias), como se observa en la Fig. 29.1, en base a los resultados de la iteración anterior (si la observación se clasificó correcta o erróneamente). Las ponderaciones más altas se aplicarán a las observaciones que fueron erróneamente clasificadas, no prestándose tanta atención a las bien clasificadas. Este proceso se repite hasta que se llega a un nivel bajo de error. El resultado final se obtiene a través de la media ponderada de las predicciones de los árboles de decisión simples. Las ponderaciones generalmente se establecen como la tasa de aprendizaje, que suele ser de pequeña magnitud.

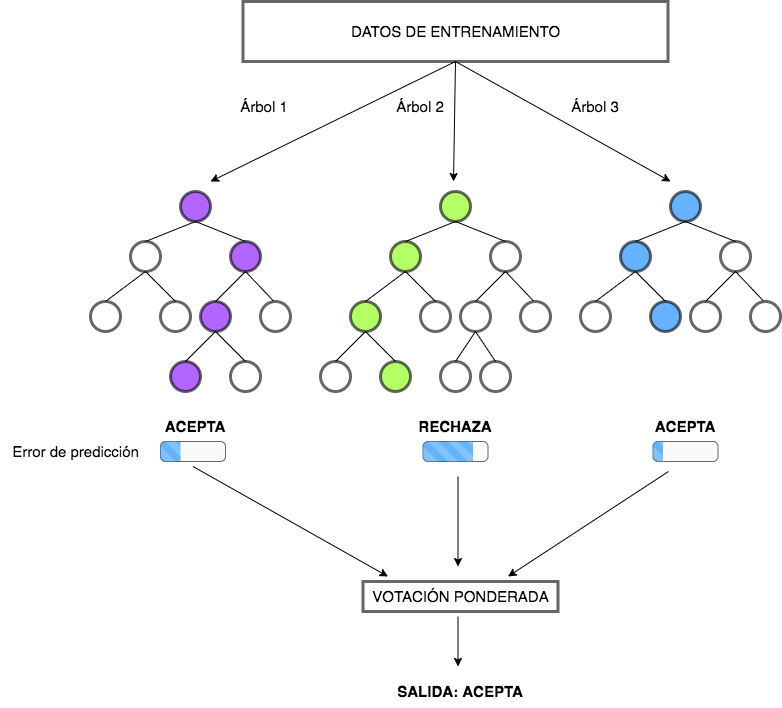
Figura 29.1: Ejemplo de \(gradient\) \(boosting\).

Matemáticamente, un algoritmo gradient boosting para clasificación sigue los pasos que se detallan a continuación. Sea un problema de clasificación binaria. Asumiendo que se tienen \(K\) árboles de clasificación, la predicción del gradient boosting se obtiene utilizando la función sigmoide, como en la regresión logística (véase Cap. 16), tal que:

\[\begin{equation} P(y=1|x,f)=\frac{1}{1+e^{-f(x)}}, \end{equation}\]

donde \(f(x)=\sum_{\kappa=1}^{K}{f_{\kappa}(x)}\) y \(f_{\kappa}\) es un árbol de decisión. De nuevo, como en la regresión logística, se aplica la estimación máximo verosímil, tratando de hallar una función \(f\) que maximice la log-verosimilitud: \(\mathcal{L}_f = \sum_{i=1}^{N}{\ln\left(P(y_i=1|x_i,f)\right)}\).

El algoritmo, en origen, es un modelo constante de la forma \(f=f_0=\frac{p}{1-p}\) donde \(p=\frac{1}{N}\sum^{N}_{i=1} x_i\). Tras cada iteración se añade un nuevo árbol al modelo; así, tras la kappa-ésima iteracción se añade el modelo (árbol) \(f_\kappa\). Para encontrar el mejor “nuevo” árbol, \(f_\kappa\), se calcula la primera derivada parcial de la log-verosimilitud, \(g_i,\hspace{0,1cm} i=1,\dots,N\):

\[\begin{equation} \frac{\delta g_i} {\delta f} = \frac{\delta\mathcal{L}_f}{\delta f}=\frac {\delta \left(P(y=1|x,f\right)}{\delta f}= \frac{\delta \left(\frac {1}{1+e^{-f(x)}}\right)} {\delta f}=\frac{1}{e^{f(x_i)}+1}, \hspace{0,3cm} i=1,\dots,N, \end{equation}\]

donde \(f\) es el modelo de clasificación ensamblado construido en la iteración previa.

A continuación, en el conjunto de entrenamiento, se reemplaza el valor de la categoría original \(y_i, \hspace{0,1cm} i=1,\dots, N\) por el que indica su correspondiente derivada parcial, \(g_i\), y se construye el “nuevo” modelo \(f_\kappa\) utilizando el conjunto de entrenamiento transformado. Una vez obtenido el nuevo modelo, se obtiene la ponderación óptima (\(\rho_\kappa\)) como:

\[\begin{equation} \rho_\kappa = \arg \max\limits_{\rho}{\mathcal{L}_{f+\rho f_\kappa}}. \end{equation}\]

Al terminar la iteración \(\kappa\), se actualiza el modelo ensamblado \(f\) añadiendo el nuevo árbol \(f_\kappa\):

\[\begin{equation} f\leftarrow f+\alpha\rho_\kappa f_\kappa. \end{equation}\]

donde \(\alpha\) es el aprendizaje en el gradiente, un valor entre 0 y 1 que controla la contribución de cada árbol débil al modelo ensamblado.

Se itera hasta que \(\kappa=K\), entonces el proceso se detiene y se obtiene el modelo ensamblado final \(f\).

29.3.1 Hiperparámetros del modelo gradient boosting

Un modelo de gradient boosting tiene dos tipos de hiperparámetros:

Hiperparámetros de boosting.
Hiperparámetros del árbol.

29.3.1.1 Hiperparámetros de boosting

Los hiperparámetros de boosting son principalmente dos: el número de árboles y la tasa de aprendizaje.

El primero indica el número de árboles a construir que, como se ha comentado, es importante optimizar para evitar el sobreajuste del modelo. A diferencia de los modelos random forest o bagging, en el boosting el conjunto de árboles débiles crece de forma secuencial para que cada árbol corrija los errores del anterior. El número de árboles necesarios para que el modelo sea buen predictor puede verse incrementado en función de los valores que tomen los otros hiperparámetros.

La tasa de aprendizaje es el hiperparámetro que determina la contribución de cada árbol al resultado final y controla la rapidez con la que el algoritmo avanza por el descenso del gradiente, es decir, la velocidad a la que aprende. Este hiperparámetro toma valores entre 0 y 1, aunque los valores habituales oscilan entre 0,001 y 0,3. Cuando esta tasa toma valores bajos, el modelo se robustece frente a las características específicas de cada árbol, permitiendo una buena generalización. Además, valores bajos de la tasa de aprendizaje facilitan también una parada temprana, antes del sobreajuste del modelo. En contraposición, los modelos se vuelven computacionalmente más exigentes, lo cual dificulta alcanzar el modelo óptimo con un número fijo de árboles. En resumen, cuanto menor sea este valor, más preciso puede ser el modelo, pero también requerirá más árboles en la secuencia.

29.3.1.2 Hiperparámetros de árbol

Los principales hiperparámetros de árbol son: la profundidad del árbol y el número mínimo de observaciones en nodos terminales, como se vio en el Cap. 24.

El primer hiperparámetro controla la profundidad de los árboles individuales. Los valores habituales de profundidad oscilan entre 3 y 8. Los árboles de menor profundidad son eficientes computacionalmente, pero menos precisos. Sin embargo, los árboles de mayor profundidad permiten que el algoritmo capture interacciones únicas, aunque aumentan el riesgo de sobreajuste.

El segundo hiperparámetro, además de controlar el número mínimo de observaciones en los nodos terminales, controla la complejidad de cada árbol. Los valores típicos de este hiperparámetro suelen estar entre 5 y 15. Los valores más altos ayudan a evitar que un modelo aprenda relaciones que pueden ser muy específicas de la muestra particular seleccionada para entrenar el árbol, evitando así el sobreajuste. Los valores más pequeños pueden ser “recomendables” en el caso de problemas de clasificación en los que las clases de la variable respuesta estén muy desequilibradas en cuanto a número de observaciones, con lo cual el número de ellas en alguna (o algunas) de las clases pudiera ser muy pequeño.

29.3.2 Estrategia de ajuste de hiperparámetros

A diferencia del random forest, la precisión de los modelos gradient boosting puede variar mucho en función de la configuración de sus hiperparámetros. Por ello, el ajuste de dichos hiperparámetros puede requerir seguir una estrategia. Una estrategia recomendable es la siguiente:

Elegir una tasa de aprendizaje relativamente alta. El valor predeterminado es 0,1 y generalmente proporciona buenos resultados. Sin embargo, para la mayoría de problemas, valores entre 0,05 y 0,2 funcionan muy bien.
Determinar el número óptimo de árboles para la tasa de aprendizaje elegida.
Ajustar los hiperparámetros del árbol y la tasa de aprendizaje y evaluar el rendimiento del modelo vs. la velocidad de aprendizaje.
Ajustar los hiperparámetros específicos del árbol para determinar la tasa de aprendizaje.
Una vez que se ajustan los parámetros específicos del árbol, se reduce la tasa de aprendizaje para evaluar cualquier mejora en la precisión.
Utilizar la configuración final de hiperparámetros y aumentar el número de grupos en el proceso de validación cruzada para obtener estimaciones más robustas. Si se utiliza validación cruzada en los pasos anteriores, entonces este paso no es necesario.

29.3.3 Procedimiento con R: la función `gbm()`

La función gbm() incluida en el paquete con el mismo nombre gbm() de R es la que se utiliza en esta sección para entrenar un modelo gradient boosting:

gbm(formula,data=..., ...)

formula: indica cuál es la variable dependiente y cuáles son las variables predictoras: \(Y \sim X_1 + ... + X_p\); los signos “+” indican un conjunto de variables predictoras y no una relación lineal con la variable dependiente (que puede o no serlo).
data: conjunto de datos con el que entrenar el árbol de acuerdo a la fórmula indicada.

29.3.4 Aplicación del modelo gradient boosting en R

Igual que en todos estos capítulos dedicados al machine learning supervisado, la implementación en R del modelo gradient boosting se lleva a cabo a partir de los datos de compras dp_entr, incluidos en el paquete CDR, con los cuales se trata de clasificar a los clientes de una empresa en compradores o no de un nuevo producto de la empresa: un tensiómetro digital. El modelo se entrena con el conjunto de datos de entrenamiento sin transformar (en su escala original). Así, en lugar de utilizar las variables categóricas transformadas mediante one-hot-encoding,²⁰¹ se usan en su escala original, como ocurre con el caso de la variable que mide el nivel educativo. En cuanto a los hiperparámetros, el método gbm (gradient boosting machine) ha elegido los valores 1, 2 y 3 para la profundidad del árbol (interaction.depth) y 50, 100 y 150 para el número de árboles (ntrees); los valores del número mínimo de observaciones en los nodos terminales (nminobsmode) y de la tasa de aprendizaje (shrinkage), toman los valores establecidos por defecto: 10 y 0,1, respectivamente.

library("CDR")
library("caret")
library("gbm")
library("reshape")
library("ggplot2")
data(dp_entr)

# se determina la semilla aleatoria
set.seed(101)

# se entrena el modelo
model <- train(CLS_PRO_pro13 ~ ., 
            data=dp_entr, 
            method="gbm", 
            metric="Accuracy",
            trControl = trainControl(classProbs = TRUE, 
                                     method = "cv", number = 10)
            )

# se muestra la salida del modelo
model

Stochastic Gradient Boosting 

558 samples
 17 predictor
  2 classes: 'S', 'N' 

No pre-processing
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 502, 502, 502, 503, 503, 502, ... 
Resampling results across tuning parameters:

  interaction.depth  n.trees  Accuracy   Kappa    
  1                   50      0.8564610  0.7130031
  1                  100      0.8690909  0.7383556
  1                  150      0.8762338  0.7526413
  2                   50      0.8690909  0.7382344
  2                  100      0.8762338  0.7526413
  2                  150      0.8799026  0.7599227
  3                   50      0.8763636  0.7528004
  3                  100      0.8781494  0.7563575
  3                  150      0.8835390  0.7671499

Tuning parameter 'shrinkage' was held constant at a value of 0.1
Tuning
 parameter 'n.minobsinnode' was held constant at a value of 10
Accuracy was used to select the optimal model using the largest value.
The final values used for the model were n.trees = 150, interaction.depth =
 3, shrinkage = 0.1 and n.minobsinnode = 10.

El modelo resultante del proceso de entrenamiento es un gradient boosting que ha ajustado los hiperparámetros a 150 árboles y una profundidad igual a 3. Además, como se avanzó, los valores del número mínimo de observaciones en los nodos terminales y de la tasa de aprendizaje fueron los valores establecidos por defecto: 10 y 0,1, respectivamente. Los resultados en el proceso de validación cruzada se muestran en la Fig. 29.2, en la que se observa cómo la precisión (accuracy) oscila entre el 84% y el 93% en las iteraciones.

ggplot(melt(model$resample[,-4]), aes(x = variable, y = value, fill=variable)) + 
  geom_boxplot(show.legend=FALSE) + 
  xlab(NULL) + ylab(NULL)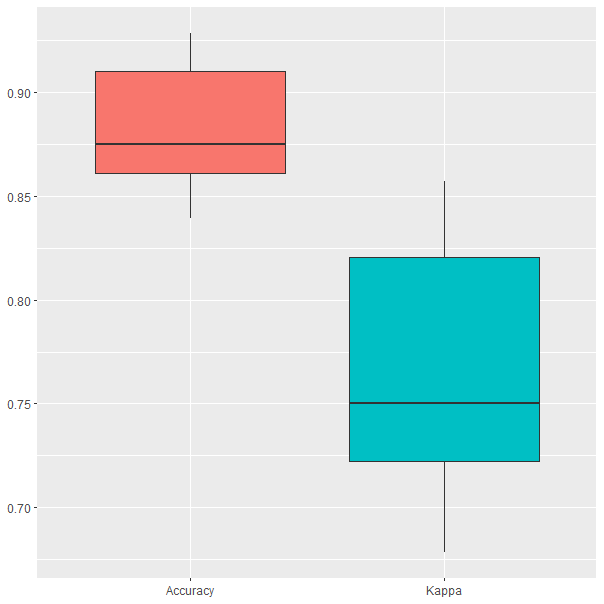

Figura 29.2: Resultados del modelo GB obtenidos durante el proceso de validación cruzada.

29.3.5 Gradient Boosting con ajuste automático

En la sección precedente los valores de los hiperparámetros se tomaron por defecto (número mínimo de observaciones en los nodos terminales y de la tasa de aprendizaje) o fueron elegidos entre los que la función gbm() establece por defecto (la profundidad del árbol y el número de árboles). En esta sección, los cuatro hiperparámetros del método gbm anteriormente referidos se ajustan de manera automática entre los valores establecidos por el investigador:

modelLookup("gbm")
model         parameter                   label forReg forClass probModel
1   gbm           n.trees   # Boosting Iterations   TRUE     TRUE      TRUE
2   gbm interaction.depth          Max Tree Depth   TRUE     TRUE      TRUE
3   gbm         shrinkage               Shrinkage   TRUE     TRUE      TRUE
4   gbm    n.minobsinnode Min. Terminal Node Size   TRUE     TRUE      TRUE

Siguiendo la estrategia descrita anteriormente, los rangos de posibles valores para los hiperparámetros a optimizar son los siguientes:

# Se especifica un rango de valores posibles para los hiperparámetros
tuneGrid <- expand.grid(interaction.depth = c(4,6,8),
                        n.trees = c(10*ncol(dp_entr),300,500), 
                        shrinkage = c(0.05,0.1,0.2), 
                        n.minobsinnode = c(5,10,15))

Esta red de posibles valores para los hiperparámetros del modelo se incorpora a la función de entrenamiento. Cuanto más exhaustiva sea la red, mayor será el tiempo de ajuste del modelo. La red presentada está formada por las 81 combinaciones posibles que se pueden llevar a cabo con los valores establecidos para los hiperparámetros.

# se fija la semilla aleatoria
set.seed(101)

# se entrena el modelo
model <- train(CLS_PRO_pro13~., 
            data=dp_entr, 
            method="gbm", 
            metric="Accuracy",
            trControl=trainControl(classProbs = TRUE,
                                   method="cv", number=10),
            tuneGrid=tuneGrid)

El modelo que mejores resultados proporciona es aquel que ajusta los hiperparámetros a los siguientes valores: 180 árboles, una profundidad igual a 6, una tasa de aprendizaje de 0,05 y un número mínimo de 10 observaciones en los nodos terminales.

# se muestra la salida del modelo
model$bestTune
   n.trees interaction.depth shrinkage n.minobsinnode
13     180                 6      0.05             10

En la Fig. 29.3 se muestran los resultados obtenidos durante el proceso de validación cruzada. Se puede ver que los resultados son similares a los del modelo anterior, aunque hay diferencias importantes. En primer lugar, se alcanza un valor máximo de precisión superior al del modelo gbm sin ajuste automático anterior, pues en este caso la precisión oscila entre el 84 % y el 95%. En segundo lugar, el valor mediano de la precisión ha aumentado desde el 87,5 % hasta el 90 %. Por último, nótese que la automatización del proceso de ajuste de los hiperparámetros no ha llevado a una gran mejoría en el rendimiento del modelo, lo que confirma lo ya expuesto sobre el buen rendimiento del modelo de gradient boosting que surge de entrenar el modelo con los valores establecidos por defecto para los hiperparámetros.

ggplot(melt(model$resample[,-4]), aes(x = variable, y = value, fill=variable)) + 
  geom_boxplot(show.legend=FALSE) + 
  xlab(NULL) + ylab(NULL)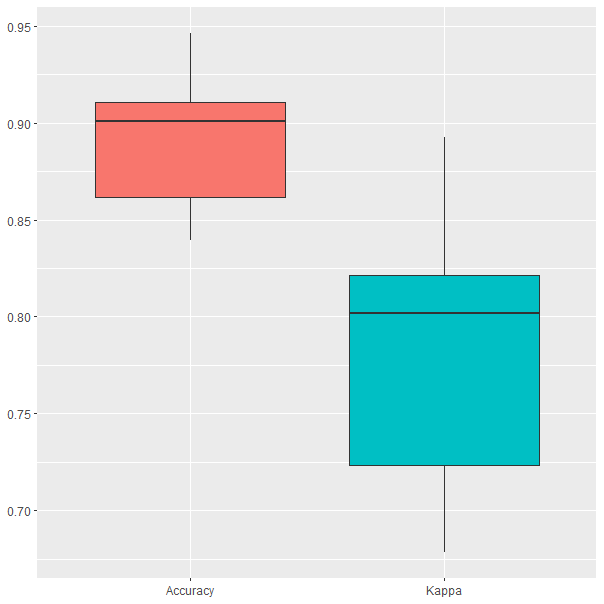

Figura 29.3: Resultados del modelo GB con ajuste automático obtenidos durante el proceso de validación cruzada.

29.4 \(\bf\textit{eXtreme}\) \(\bf\textit{gradient}\) \(\bf\textit{boosting}\)

El eXtreme Gradient Boosting es una implementación eficiente y escalable del modelo gradient boosting. Este modelo, abreviado como XGBoost, es un paquete de código abierto en C++, Java, Python (Wade, 2020), R, Julia, Perl y Scala. En R, el modelo se incluye dentro del paquete xgboost (Chen et al., 2015). El paquete incluye un procedimiento para la solución eficiente de modelos lineales y un algoritmo de aprendizaje de árboles.

Xgboost es compatible con funciones objetivo de regresión, clasificación y ranking. Además, tiene varias características importantes:

Velocidad: xgboost puede realizar automáticamente cálculos paralelos. Por lo general, es 10 veces más rápido que el modelo gradient boosting.
Tipo de entrada: xgboost toma varios tipos de datos de entrada en R:

Matriz densa (matrix).
Matriz dispersa (Matrix::dgCMatrix).
Archivo de datos locales.
Un tipo de datos propio del paquete: xgb.DMatrix.

Dispersión: xgboost acepta datos de entrada dispersos para los modelos incluidos.
Personalización: xgboost admite tanto funciones de objetivo y funciones de evaluación personalizadas.
Rendimiento: xgboost alcanza generalmente una mayor precisión que gradient boosting.

29.4.1 Hiperparámetros del modelo XGBoost

Xgboost proporciona no solo los hiperparámetros del gradient boosting, sino también otros adicionales que pueden servir de ayuda a la hora de reducir las posibilidades de sobreajuste, lo que lleva a una menor varianza de predicción y, por lo tanto, a una mayor precisión. Estos hiperparámetros son los de regularización y el de dropout (descarte).

Los parámetros de regularización se incluyen para ayudar a evitar el sobreajuste y reducir la complejidad del modelo. Existen tres hiperparámetros que tienen esta función: gamma (\(\gamma\)), alpha (\(\alpha\)) y lambda (\(\lambda\)). El hiperparámetro \(\gamma\) es un hiperparámetro de pseudorregularización, conocido como multiplicador Lagrangiano, tal que para hacer una partición adicional en un nodo es necesaria que la reducción en la pérdida (medida por SSE o similar) sea superior a la especificada por gamma. Es un hiperparámetro de poda; así, el modelo XGBoost hace crecer los árboles hasta una profundidad máxima establecida, pero en el proceso de poda eliminará las divisiones que no cumplan con la regularización \(\gamma\). Este hiperparámetro toma valores entre 0 e infinito (\(\infty\)), siguiendo la regla de que cuanto mayor sea su valor, mayor será la regularización. Los otros hiperparámetros de regularización, \(\alpha\) y \(\lambda\), son más clásicos. Mientras que \(\alpha\) proporciona una regularización \(L_1\), \(\lambda\) proporciona una regularización \(L_2\). Estos parámetros de regularización establecen un límite a a la magnitud de los pesos de los nodos en un árbol. Sus valores se encuentran, al igual que los de \(\gamma\), entre 0 y \(\infty\). Tanto \(\alpha\) como \(\lambda\) hacen que el modelo sea más conservador al aumentar su valor.

El dropout es un enfoque alternativo para reducir el sobreajuste. Cuando se entrena un modelo de gradient boosting, los primeros árboles tienden a dominar el rendimiento del modelo, mientras que los que se agregan después suelen mejorar la predicción solo para un pequeño grupo de variables. Esto puede llevar a que se incremente el riesgo de sobreajuste. Con el dropout, se descartan árboles aleatoriamente en el proceso de entrenamiento.

En su implementación en R, el modelo XGBoost incluye principalmente los siguientes hiperparámetros: número de iteraciones, profundidad máxima de los árboles, tasa de aprendizaje y regularización \(\gamma\).

head(modelLookup("xgbTree"),4)
    model parameter                  label forReg forClass probModel
1 xgbTree   nrounds  # Boosting Iterations   TRUE     TRUE      TRUE
2 xgbTree max_depth         Max Tree Depth   TRUE     TRUE      TRUE
3 xgbTree       eta              Shrinkage   TRUE     TRUE      TRUE
4 xgbTree     gamma Minimum Loss Reduction   TRUE     TRUE      TRUE

29.4.2 Procedimiento con R: la función `xgboost()`

La función xgboost() del paquete xgboost de R se utiliza en esta sección para entrenar un modelo extreme gradient boosting:

xgboost(data = ..., label = ..., ...)

data: conjunto de datos con el que entrenar el modelo.
label: vector con la variable respuesta.

29.4.3 Aplicación del modelo XGBoost en R

Este modelo se entrena utilizando el conjunto de entrenamiento sin transformar (en su escala original). Para ilustrar su implementación en R, sin y con ajuste automatizado de los hiperparámetros, se retoma el ejemplo utilizado en la implementación del modelo gradient boosting.

Se considera primeramente el entrenamiento del modelo con los valores que asigna por defecto la función xgboost() a los hiperparámetros: para la regularización \(\gamma=1\) (0) y para el tamaño mínimo del nodo (n.minobsinnode= 1). Los demás hiperparámetros sí se ajustan.

# se determina la semilla aleatoria
set.seed(101)

# se entrena el modelo
model <- train(CLS_PRO_pro13~.,
               data=dp_entr,
               method="xgbTree",
               metric="Accuracy",
               trControl=trainControl(classProbs = TRUE,
                                      method = "cv",
                                      number=10))

El modelo XGBoost resultante tiene 50 iteraciones, una profundidad máxima igual a 2 y una tasa de aprendizaje de 0,3. Los resultados de la validación cruzada (Fig. 29.4) muestran que la precisión obtenida oscila entre el 85% y el 95%, resultado similar al del gradient boosting con hiperparámetros ajustados. Sin embargo, el valor mediano de la precisión es del 88%, ligeramente inferior al observado en el modelo gradient boosting con ajuste automático.

ggplot(melt(model$resample[,-4]), aes(x = variable, y = value, fill=variable)) + 
  geom_boxplot(show.legend=FALSE) + 
  xlab(NULL) + ylab(NULL)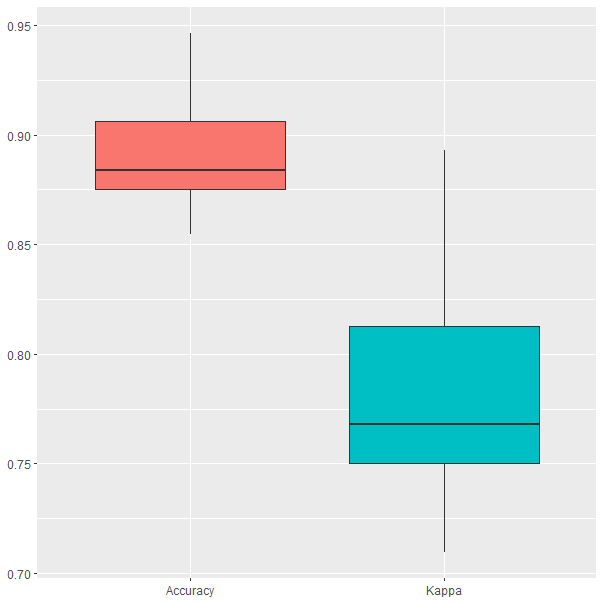

Figura 29.4: Resultados del modelo durante la validación cruzada.

29.4.4 XGBoost con ajuste automático

En esta sección los hiperparámetros más relevantes del modelo se ajustan automáticamente. Para ello se genera una red de posibles valores para tales hiperparámetros. Por motivos computacionales, esta no se hace excesivamente exhaustiva (para evitar largos tiempos de entrenamiento). Sin embargo, si se dispone de tiempo suficiente para el entrenamiento, es aconsejable ampliar dicha red.

# Se especifica un rango de valores típicos para los hiperparámetros
tuneGrid <- expand.grid (nrounds=c(50,100,500), 
                         max_depth = c(3,4,8),
                         eta =c(0.05,0.1,0.2,0.3),
                         gamma=c(0,0.5,5),
                         colsample_bytree=c(0.8),
                         min_child_weight=c(5),
                         subsample=c(0.5))

# se determina la semilla aleatoria
set.seed(101)

# se entrena el modelo
model <- train(CLS_PRO_pro13~., 
               data=dp_entr, 
               method="xgbTree", 
               metric="Accuracy",
               trControl=trainControl(classProbs = TRUE,
                                      method = "cv",
                                      number = 10),
               tuneGrid=tuneGrid)

# se muestra la salida del modelo
model$bestTune[,1:4]
   nrounds max_depth eta gamma
71     100         4 0.2     5

Como puede verse en los resultados obtenidos, el modelo resultante establece que se utilicen 100 iteraciones, que los árboles tengan una profundidad máxima de 4, que la tasa de aprendizaje sea 0,2 y que la regularización \(\gamma\) tome el valor 5.²⁰²

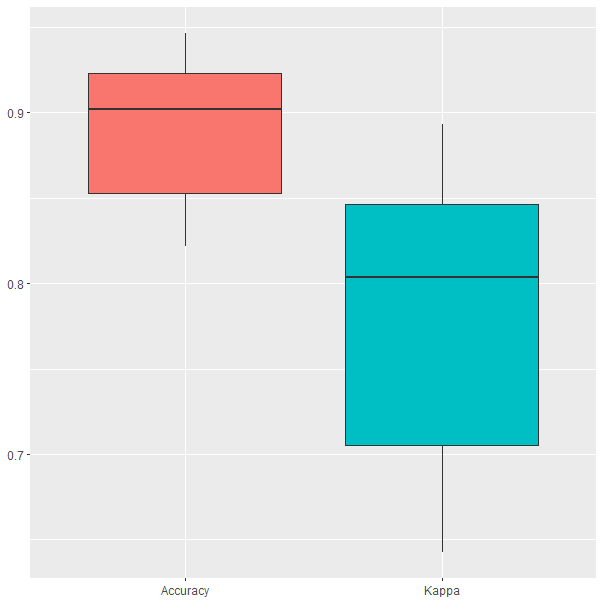
Figura 29.5: Resultados del modelo durante la validación cruzada.

Los resultados obtenidos durante la validación cruzada (Fig. 29.5) muestran que la precisión es muy similar a la del modelo de la sección anterior (entre el 85% y el 95%); sin embargo, el valor mediano de la precisión aumenta hasta el 90%.

Resumen

En este capítulo se introduce al lector en el algoritmo de aprendizaje supervisado conocido como gradient boosting. En concreto:

Se presenta el segundo de los paradigmas de aprendizaje ensamblado: el boosting.
Se explica el modelo basado en este paradigma, el gradient boosting, así como sus diferencias con el bagging y el random forest.
Se exponen los hiperparámetros más relevantes a la hora de optimizar un modelo de gradient boosting.
Se presenta el eXtreme gradient boosting, una implementación eficiente y escalable del modelo gradient boosting, y se comentan los hiperparámetros de regularización y otros parámetros importantes en esta implementación.
Se aplican ambos algoritmos en R a un caso práctico de clasificación binaria de datos.

28 Métodos ensamblados: \(\bf \textit {bagging}\) y \(\bf \textit{random}\) \(\bf \textit{forest}\)

30 Análisis clúster: clusterización jerárquica