Capítulo 14 Muestreo y remuestreo
Mª Leticia Meseguer Santamaría\(^{a}\) y Manuel Vargas Vargas\(^{a}\)
\(^{a}\) Universidad de Castilla-La Mancha
14.1 Introducción al muestreo
Muchas investigaciones científicas abordan el estudio de características de un conjunto de elementos, que se denomina población. Sin embargo, no siempre es posible estudiar la totalidad del colectivo, por problemas de accesibilidad, confidencialidad, costes económicos o temporales, etc. En estos casos, se recurre a extraer un subconjunto de la población que se pretende que sea representativo de esta respecto a las características estudiadas. El objetivo es obtener información relevante que pueda extrapolarse al total de la población, proceso denominado genéricamente muestreo.
En otros casos, la conveniencia de muestrear una población está relacionada con la credibilidad de los resultados obtenidos o de las propiedades de los modelos utilizados. Así, muchas técnicas cuantitativas dividen la información (muestra) disponible en un subconjunto de entrenamiento o estimación y otro de contraste o validación; una elección inadecuada puede alterar los resultados e invalidar las conclusiones. Por último, caso muy común en ciencias sociales, no se puede acceder a la medición directa de los fenómenos (por ser una población muy grande o un fenómeno subjetivo), por lo que se accede a ella mediante encuestas, que precisan de una metodología de muestreo rigurosa y diseñada previamente.
Para fijar terminología, se define población como el conjunto de casos de interés a los que se quieren generalizar los resultados de la investigación, denominados genéricamente individuos; a veces, solo es posible acceder a una parte de la población, por lo que se utiliza el término población objetivo para el conjunto total y población muestreable al conjunto al que se tiene acceso. Por coherencia, cuando ambos colectivos no coincidan, los resultados deben extrapolarse solo al último de ellos.
Las características de interés de la población se consideran variables, en el sentido estadístico del término, por lo que son estudiadas mediante su distribución. En algunos casos, esta será completamente desconocida, siendo de interés su determinación completa; en otros muchos, se buscará determinar sólo algunos aspectos (medidas de posición, dispersión, etc.) o los parámetros que rigen una distribución funcionalmente conocida. En todo caso, el objetivo del estudio es determinar la distribución estadística de estas variables, conocida como distribución poblacional; a veces, por simplicidad en el lenguaje, a esta distribución o, incluso, a las variables, se las denomina población (por ejemplo, no es infrecuente encontrar enunciados del tipo “la población sigue una distribución binomial”, identificando población con variable, o “la población es una distribución normal”, identificando población con distribución).
Se define muestra como un subconjunto de la población, que será utilizado para caracterizar la distribución poblacional y unidad muestral a cada individuo de la muestra. Si la muestra tiene la misma distribución que la población, se dice que es representativa, mientras que en caso contrario se denomina sesgada.
Siempre será preferible un método de muestreo que proporcione muestras representativas, característica ligada a la forma de seleccionar la muestra y al tamaño de esta. Así, siempre que sea posible, se recomienda utilizar un muestreo probabilístico, basado en la selección aleatoria de la muestra (conociéndose, por tanto, la probabilidad de que cada individuo salga seleccionado), lo que permite extender los resultados a toda la población, cuantificando posibles sesgos y detallando un error máximo dentro de un nivel de confianza seleccionado al inicio del proceso.
No siempre será posible utilizar un muestreo probabilístico, por lo que existe una colección de métodos de muestreo no probabilístico (conveniencia, bola de nieve, cuotas, etc.), que no se detallarán en este capítulo. La característica común a todos ellos es que los resultados obtenidos de la muestra no se deben extrapolar a la población, ya que no está garantizada la representatividad.
En el resto del capítulo se presentarán brevemente los métodos de muestreo probabilístico más usuales. Para mayor detalle, se pueden consultar las referencias Chaudhuri & Stenger (2005), Arnab (2017) o Wu & Thompson (2020).
14.2 Muestreo aleatorio simple
El método básico de muestreo es el conocido como muestreo aleatorio simple (m.a.s.), ya introducido en la Sec. 13.2, consistente en seleccionar totalmente al azar a los individuos de la muestra, por lo que todos tienen la misma probabilidad de formar parte de ella. Si cada individuo solo puede aparecer una vez en la muestra, se habla de muestreo aleatorio sin reemplazamiento o muestreo aleatorio irrestricto, mientras que, en caso contrario, se denomina muestreo con reemplazamiento o, en general, muestreo aleatorio simple.111
Este procedimiento es el que se asume en la inmensa mayoría de las técnicas estadísticas convencionales, pero presenta dos inconvenientes. En primer lugar, presupone que existe un registro, o listado, completo de todos los individuos de la población (lo que no siempre es posible), y su aplicación práctica puede resultar costosa (en medios, tiempo y dinero). En segundo lugar, presupone que la característica estudiada es homogénea en todos los individuos de la población, es decir, la distribución poblacional es idéntica en todos los individuos. Frecuentemente, esta homogeneidad poblacional no se cumple, por lo que sería necesario abordar otros métodos de muestreo que se expondrán más adelante. En todo caso, si se utiliza un m.a.s., la heterogeneidad induce un aumento de la variabilidad muestral, hecho que debe ser tenido en cuenta en la interpretación de resultados.
Además de la forma de selección, el factor que determina la representatividad de una muestra es su tamaño (véase el teorema de Glivenko-Cantelli mostrado en la ecuación (13.3)). Al utilizar la información muestral para aproximar los aspectos o parámetros desconocidos en la población se comete el llamado error muestral, que representa el margen de error que se está dispuesto a aceptar (por tanto, está íntimamente relacionado con los intervalos de confianza)112; si el tamaño de la muestra está determinado, el margen de error muestral marca el grado de precisión con el que se pueden extrapolar los resultados. Una alternativa es predeterminar un error muestral a cierto nivel de confianza y calcular cuál es el menor tamaño muestral que cumple ese requisito.
El margen de error (o simplemente error muestral), \(\epsilon\), depende del aspecto o parámetro poblacional que se quiera conocer (frecuentemente, la media, el total poblacional o la proporción), del estimador utilizado y del nivel de confianza. Si se asume una distribución poblacional normal, la expresión general sería:
\[\begin{equation} \tag{14.1} \epsilon_\alpha = z_{1-\alpha/2}\sigma(\hat \theta), \end{equation}\]
expresión que es frecuentemente extrapolada a distribuciones poblacionales no normales.
Para el caso de estimar la media poblacional utilizando la media muestral, sustituyendo en la ecuación anterior (14.1), la relación entre error muestral, nivel de confianza y tamaño muestral sería:
\[\begin{equation} \tag{14.2} \epsilon_\alpha = z_{1-\alpha/2}\sqrt{(1-{n\over N}) {s^2 \over n}}. \end{equation}\]
Operando y despejando el tamaño muestral, se obtiene la expresión:
\[\begin{equation} \tag{14.3} n = {z^2_{1-\alpha/2} Ns^2 \over N\epsilon^2_\alpha + z^2_{1-\alpha/2}s^2}. \end{equation}\]
En algunos casos se considera que se está muestreando una población de tamaño infinito, lo que produce una simplificación de la fórmula de obtención del tamaño muestral:
\[\begin{equation} \tag{14.4} \epsilon_\alpha = z_{1-\alpha/2}\sqrt{s^2 \over n} \Longrightarrow n = {z^2_{1-\alpha/2} s^2 \over \epsilon^2_\alpha}. \end{equation}\]
Si se está interesado en estimar el total poblacional, un procedimiento análogo conduce a las ecuaciones:
\[\begin{equation} \tag{14.5} \epsilon_\alpha = z_{1-\alpha/2}\sqrt{N^2(1-{n\over N}) {s^2 \over n}} \Longrightarrow n = {z^2_{1-\alpha/2} N^2s^2 \over \epsilon^2_\alpha + z^2_{1-\alpha/2}Ns^2}. \end{equation}\]
Por último, si se desea estimar la proporción poblacional, \(P\), de individuos que cumplen algún criterio, se puede particularizar el caso del estimador de la media poblacional sobre una población binomial, por lo que el resultado obtenido es:
\[\begin{equation} \tag{14.6} n = {z^2_{1-\alpha/2} Npq \over (N-1)\epsilon^2_\alpha + z^2_{1-\alpha/2}pq}, \end{equation}\]
siendo \(q=1-p\).
En la práctica es muy frecuente que se desconozca la varianza poblacional, por lo que se suele recurrir a alguna estimación previa, con lo que se tiene una aproximación al tamaño muestral requerido.
14.2.1 Ejemplo de m.a.s. en R
Para ejemplificar el proceso de obtención de una muestra aleatoria simple en R, se usará el paquete samplingbook y el conjunto de datos iris, correspondiente a las medidas, en centímetros, de largo y ancho de los sépalos y pétalos de 150 flores, equidistribuidas entre las especies setosa, versicolor y virginica.
library("samplingbook")
datos_ej <- data.frame(iris)En este caso, por simplicidad, se considerará que la población es el conjunto de las 150 flores disponibles, y que se desea una muestra aleatoria simple con reemplazamiento para determinar la longitud media de los sépalos con un error de 0,3 centímetros al 95% de confianza. La función sample.size.mean() permite calcular el tamaño de muestra necesario para cumplir estos requisitos.113
sd <- sd(datos_ej$Sepal.Length) # Se considera como la desviación típica poblacional
N <- nrow(datos_ej) # Tamaño de la población
e <- 0.3 # Margen de error prefijado
sample.size.mean(e, sd, N, level = 0.95)
#>
#> sample.size.mean object: Sample size for mean estimate
#> With finite population correction: N=150, precision e=0.3 and standard deviation S=0.8281
#>
#> Sample size needed: 25Así, basta con una muestra aleatoria simple de tamaño 25 para poder estimar la longitud media de los sépalos con los requisitos dados. Para obtener la muestra concreta, la función sample proporciona los valores obtenidos (conjunto de 25 valores aleatorios entre 1 y N=150) y permite seleccionar los casos que conforman la muestra:
set.seed(196) # Fija la semilla de aleatorización para poder reproducir los resultados
muestra <- sample(1:N, 25, replace = TRUE) # Si se quisiera un muestreo sin reemplazo, se utilizaría la sentencia replace=FALSE
datos_muestra <- datos_ej[muestra, ] # Se seleccionan los datos que conforman la muestra
head(datos_muestra)
#> Sepal.Length Sepal.Width Petal.Length Petal.Width Species
#> 122 5.6 2.8 4.9 2.0 virginica
#> 133 6.4 2.8 5.6 2.2 virginica
#> 104 6.3 2.9 5.6 1.8 virginica
#> 95 5.6 2.7 4.2 1.3 versicolor
#> 95.1 5.6 2.7 4.2 1.3 versicolor
#> 73 6.3 2.5 4.9 1.5 versicolorPara finalizar, usando la función Smean() se puede obtener la estimación de la media poblacional, así como su error estándar y un intervalo de confianza. Aunque en la práctica el valor poblacional es desconocido, en este ejemplo sí se puede obtener a partir del conjunto de todos los datos, lo que permite comparar la estimación con el verdadero valor buscado.
Smean(datos_muestra$Sepal.Length, N, level = 0.95)
#>
#> Smean object: Sample mean estimate
#> With finite population correction: N=150
#>
#> Mean estimate: 5.976
#> Standard error: 0.1115
#> 95% confidence interval: [5.7575,6.1945]
mean(datos_ej$Sepal.Length) # Valor de la media poblacional
#> [1] 5.843333En este ejemplo, el error cometido sería de 5,976 - 5,843 = 0,133 cm.
Si interesa estimar el total poblacional, basta con multiplicar la estimación de la media por el tamaño poblacional, \(N\). Por último, si se desea estimar una proporción poblacional, el proceso sería idéntico al descrito, pero usando la función Sprop().
14.3 Muestreo estratificado
Una consecuencia del muestreo aleatorio simple es que “reproduce” las características de la población, entre otros aspectos, su variabilidad, que se asumen comunes a todos los individuos. Sin embargo, es frecuente que haya “grupos” de individuos que presenten diferencias en los parámetros que rigen la distribución poblacional (por ejemplo, en sus medias o en sus varianzas) de la característica que se quiere estudiar.
En el ejemplo anterior (14.2.1), se ha muestreado para estimar la longitud media de los sépalos de las 150 flores recogidas en los datos. Sin embargo, al calcular la media y la desviación típica agrupando según la especie:
library("plyr")
estratos <- ddply(datos_ej, .(Species), summarize,
media.sl = mean(Sepal.Length),
desv.sl = sd(Sepal.Length)
)
estratos
#> Species media.sl desv.sl
#> 1 setosa 5.006 0.3524897
#> 2 versicolor 5.936 0.5161711
#> 3 virginica 6.588 0.6358796puede observarse que las tres especies no se comportan igual respecto al parámetro de interés (longitud media de los sépalos). La especie setosa presenta unos valores menores de longitud media y desviación típica, mientras que la especie virginica presenta los valores más elevados.
Si no se considerara la especie, un muestreo aleatorio simple podría sesgar los resultados, por ejemplo, con un predominio de las setosa o de las virginica. En todo caso, la variabilidad del conjunto de datos es más elevada que en cualquiera de las especies, pues a la variación dentro de cada especie se une la variación entre especies. Este hecho hace aumentar el tamaño muestral necesario para estimar con un margen de error prefijado.
En general, cuando existen grupos de individuos con un comportamiento más homogéneo dentro del grupo y diferenciado entre grupos, no resulta apropiado aplicar un m.a.s. En estos casos, es recomendable el denominado muestreo estratificado, donde se realiza previamente una partición de la población en estratos y se selecciona una m.a.s. dentro de cada grupo.
La estratificación presenta ventajas, como el aumento de la representatividad de la muestra (se necesita un menor tamaño muestral total que en el m.a.s.), la reducción del error muestral (la variabilidad es menor en cada estrato) y el incremento de probabilidad de representación en la muestra de grupos con características diferenciadas. Por el contrario, no siempre resulta evidente la relación entre la variable de estratificación y las de interés.
Una de las decisiones que se han de tomar en el muestreo estratificado es el reparto de tamaño muestral entre los distintos estratos, procedimiento conocido como afijación. Las dos opciones más utilizadas son la afijación proporcional, que reparte el tamaño muestral en función de los tamaños poblacionales de cada estrato, y la afijación óptima, que considera también los diferentes valores de la variabilidad dentro de cada estrato.
Para ejemplificar el proceso de muestreo estratificado en el caso de la base de datos utilizada, se procede a considerar cada especie de iris como un estrato, ya que se ha comprobado que presentan distintas distribuciones poblacionales respecto a la variable longitud del sépalo. Como en la Sec. 14.2.1, se quiere estimar la longitud media de la variable con un margen de error de 0,3 al 95% de confianza. Dentro del paquete samplingbook se puede utilizar la función stratasize() para determinar el tamaño muestral que cumple estos requisitos
stratasize(e, Nh = c(50, 50, 50), Sh = estratos[, 3], level = 0.95)
#>
#> stratamean object: Stratified sample size determination
#>
#> type of sample: prop
#>
#> total sample size determinated: 11Como se aprecia, para garantizar al 95% de confianza un margen de error de 0,3 cm es necesario un tamaño muestral de 11, sensiblemente inferior al requerido con un m.a.s. (25). Una vez determinado el tamaño, el criterio de afijación elegido distribuye la muestra entre los estratos.
stratasamp(n = 11, Nh = c(50, 50, 50), Sh = estratos[, 3], type = "prop")
#>
#> Stratum 1 2 3
#> Size 4 4 4
stratasamp(n = 11, Nh = c(50, 50, 50), Sh = estratos[, 3], type = "opt")
#>
#> Stratum 1 2 3
#> Size 3 4 5Como los tres estratos tienen el mismo tamaño poblacional, la afijación proporcional distribuye la muestra equitativamente; sin embargo, la afijación óptima, al considerar las diferencias en variabilidad, asigna más muestra al estrato con mayor variabilidad y menos muestra al de menor variabilidad (como los tamaños muestrales son necesariamente números enteros, se puede producir una ligera diferencia entre el tamaño muestral calculado globalmente y la suma de los tamaños de cada estrato).
Con la afijación óptima estimada, se procede a la selección de la submuestra en cada estrato (m.a.s.) y a la obtención de los datos que conforman la muestra.
set.seed(195) # Fija la semilla de aleatorización
muestra1 <- sample(1:50, 3, replace = TRUE)
muestra2 <- sample(51:100, 4, replace = TRUE)
muestra3 <- sample(101:150, 5, replace = TRUE) # m.a.s. en cada estrato
muestra_estr <- c(muestra1, muestra2, muestra3)
datos_muestra_estr <- datos_ej[muestra_estr, ] # Selección de los datos que conforman la muestra
datos_muestra_estr
#> Sepal.Length Sepal.Width Petal.Length Petal.Width Species
#> 26 5.0 3.0 1.6 0.2 setosa
#> 38 4.9 3.6 1.4 0.1 setosa
#> 5 5.0 3.6 1.4 0.2 setosa
#> 61 5.0 2.0 3.5 1.0 versicolor
#> 61.1 5.0 2.0 3.5 1.0 versicolor
#> 65 5.6 2.9 3.6 1.3 versicolor
#> 58 4.9 2.4 3.3 1.0 versicolor
#> 147 6.3 2.5 5.0 1.9 virginica
#> 146 6.7 3.0 5.2 2.3 virginica
#> 134 6.3 2.8 5.1 1.5 virginica
#> 130 7.2 3.0 5.8 1.6 virginica
#> 141 6.7 3.1 5.6 2.4 virginicaFinalmente, usando la función Smean() se obtiene la estimación de la media poblacional, así como su error estándar y un intervalo de confianza, al igual que se hizo con el m.a.s.
Smean(datos_muestra_estr$Sepal.Length, N, level = 0.95)
#>
#> Smean object: Sample mean estimate
#> With finite population correction: N=150
#>
#> Mean estimate: 5.7167
#> Standard error: 0.2393
#> 95% confidence interval: [5.2476,6.1857]14.4 Otros tipos de muestreo probabilístico
Existen otros métodos de muestreo probabilístico que buscan simplificar la extracción de una muestra representativa, entre los que destacan el muestreo por conglomerados y el muestreo sistemático.
Cuando la población es muy grande, es frecuente que se puedan establecer (o construir a partir de alguna variable) subgrupos, o clústeres, que tengan las mismas características que todo el conjunto respecto a la variable de interés. En esos casos, a efectos de estimación, sería equivalente muestrear toda la población o solo un clúster, con el consiguiente ahorro de tamaño muestral, tiempo y coste. Es el conocido como muestreo por conglomerados.
Por ejemplo, se puede estar interesado en estimar el tiempo medio que el alumnado de educación secundaria obligatoria (ESO) dedica a estudiar matemáticas en España. Obtener una muestra para todo el país puede ser costoso en tiempo, recursos materiales y tamaño muestral; sin embargo, se puede asumir que no existen diferencias entre provincias respecto a esta variable, por lo que sería posible muestrear solo en una provincia (o pocas). En este caso, el muestreo por conglomerados consistiría en una primera etapa de selección aleatoria de clústeres (provincia/s en este ejemplo) y, posteriormente, aplicar un método de muestreo sobre dicha selección (que, a su vez, podría ser un m.a.s. o un muestreo estratificado).
No conviene confundir los conceptos de estrato y clúster, aunque ambos sean subgrupos de la población total. En el primer caso, los individuos de cada estrato son muy homogéneos entre sí y diferenciados del resto de estratos. En el segundo caso, los individuos de cada clúster tienen la misma variabilidad que el conjunto de la población, no habiendo diferencias entre clústers respecto a la variable de interés. Así, la ganancia en el muestreo estratificado proviene de trabajar con menores variabilidades intraestratos, mientras que en el muestreo por conglomerados proviene de utilizar una subpoblación más pequeña.
En otras situaciones, si se dispone de un marco poblacional (listado completo de los individuos), es posible plantear un mecanismo sencillo de obtención de la muestra. Si se tiene un tamaño poblacional \(N\) y se quiere una muestra de tamaño \(n\), se pueden establecer \(k=N/n\) bloques, elegir al azar un número entre 1 y \(k\) (que permite seleccionar el primer elemento de la muestra) y, a partir de esa posición, dar saltos de magnitud \(k\) en el listado para seleccionar el resto de unidades muestrales. Es el método conocido como muestreo sistemático o, más técnicamente, muestreo sistemático uniforme de paso \(k\).
Como ejemplo, supóngase que se quiere obtener una muestra de 50 individuos en una población de 2.000. El paso sería k = 2.000/50 = 40 unidades y se selecciona aleatoriamente una unidad entre las 40 primeras (supóngase que la número 13); el resto de la muestra se obtendría sumándole el paso a la primera seleccionada (13, 53, 93, 133, 173, y así hasta la 1.973).
Por último, los métodos expuestos no son incompatibles, sino que se pueden combinar por etapas, dando lugar a los conocidos como muestreos polietápicos. Por ejemplo, la Encuesta de Población Activa, elaborada por el Instituto Nacional de Estadística, adopta un muestreo bietápico, en primer lugar, estratificado entre secciones censales y, en segundo lugar, muestreando entre las viviendas familiares de cada sección.
14.5 Técnicas de remuestreo: \(\bf{\textit{bootstrap}}\)
Cuando se infiere una característica poblacional a partir de una muestra, solo se dispone del valor concreto que el estadístico toma sobre dicha muestra. Salvo en raras ocasiones, no se dispone de su distribución en el muestreo, o solo se tiene una aproximación asintótica, por lo que no se pueden evaluar sus propiedades estadísticas con tamaños muestrales no elevados. En otros casos, es la complejidad analítica de muchas técnicas actuales de análisis de datos la que dificulta la determinación de la distribución de las estimaciones de los parámetros.
En estos casos, el método bootstrap propone sustituir la distribución poblacional (desconocida) por una estimación conocida (como puede ser la distribución empírica o una aproximación paramétrica) que, mediante remuestreo, sirva para generar muestras aleatorias a partir de la muestra original. Se obtiene así una distribución de remuestreo, llamada también distribución bootstrap, cuyo comportamiento sobre la estimación aproxima a la de la distribución muestral en torno al parámetro, lo que permite evaluar la precisión de las estimaciones.
El método bootstrap más sencillo, llamado bootstrap uniforme o bootstrap naïve, parte de la aproximación de la distribución poblacional por la distribución empírica de la muestra. Supóngase que se tiene una muestra \(X=(x_1,...,x_n)\) que es utilizada para obtener un estimador \(T(X)=\hat{\theta}\) para un parámetro poblacional \(\theta\). Utilizando su distribución empírica (véase ecuación (13.2)):
Se genera una primera muestra \(X^{*1}=(x_1^{*1},...,x_n^{*1})\), obtenida mediante muestreo aleatorio simple con reemplazamiento de la muestra original, que permite evaluar el estadístico \(T^{*1}(X^{*1})=\hat{\theta^{*1}}\).
Siguiendo el mismo procedimiento, se puede generar un número elevado (\(B\)) de muestras bootstrap, \(X^{*1}, ..., X^{*B}\), que permiten obtener el valor del estadístico sobre cada una de ellas \(T^{*1}(X^{*1}), ..., T^{*B}(X^{*B})\).
Con estos valores, se obtiene la distribución bootstrap. Por ejemplo, se puede utilizar esta distribución para calcular la media bootstrap del estadístico \(T(X)\), \(\bar {T}^*= {1 \over B} \sum_{b=1}^B T^*(X^{*b})\), y cuyo error estándar es:
\[\begin{equation} \tag{14.7} \hat{S}_{boot}= \sqrt{{1 \over {B-1}} \sum_{b=1}^B \left ( T(X^{*b})-\bar{T}^* \right ) ^2}, \end{equation}\]
expresión que aproxima al error del estadístico \(T(X)\) para estimar \(\theta\).
14.5.1 Ejemplo de bootstrap con R
Los datos sobre calidad del aire en la ciudad de Nueva York (airquality) recogen la variable Temp que mide la temperatura, en grados Fahrenheit, entre el día 1 de mayo y el 30 de septiembre. Se ha visto en la Sec. 13.7 que no se puede asumir que dicha variable esté generada por una distribución normal, por lo que no se podrían utilizar los intervalos de confianza mostrados en la Sec. 13.6.
El objetivo es calcular una estimación de la temperatura media y dar un intervalo al 95% de confianza.
En este ejemplo, se utiliza la muestra para obtener un valor del estadístico media muestral (\(\bar X\) = 77,88), estimador insesgado de la media poblacional. Sin embargo, al no conocer la distribución en el muestreo (no se asume ningún tipo de distribución poblacional ni se puede hacer uso de aproximaciones asintóticas), no se podría construir un intervalo de confianza.
Aplicando el método bootstrap (en su versión uniforme), se van a obtener 5.000 muestras de tamaño 20, mediante remuestreo con reemplazamiento:
set.seed(196) # Se fija la semilla para permitir la reproducibilidad
B <- 5000 # Se fija el número de remuestras
muestras_boot <- numeric(B) # Se almacenan todos los valores del estadístico
for (k in 1:B) {
remuestra <- sample(airquality$Temp, 20, replace = TRUE)
muestras_boot[k] <- mean(remuestra)
}
media_boot <- mean(muestras_boot)
media_boot # Media de los 5000 valores medios de las remuestras
#> [1] 77.87309
desv_boot <- sd(muestras_boot)
desv_boot # Desviación típica de los 5000 valores medios de las remuestras
#> [1] 2.090255Para construir los intervalos de confianza, se calculan los valores críticos al 95% de confianza sobre la distribución empírica de los valores medios remuestreados:
val_crit <- quantile(muestras_boot, c(0.025, 0.975))
val_crit # Valores críticos
#> 2.5% 97.5%
#> 73.75 81.95Así, con el método bootstrap, no es necesario asumir ninguna distribución en el muestreo. Aún así, la representación gráfica de la distribución empírica de los valores medios remuestreados y los extremos del intervalo de confianza (Fig. 14.1) muestran cómo la distribución de las remuestras sobre el estadístico se asemeja a la distribución del estadístico sobre el parámetro.
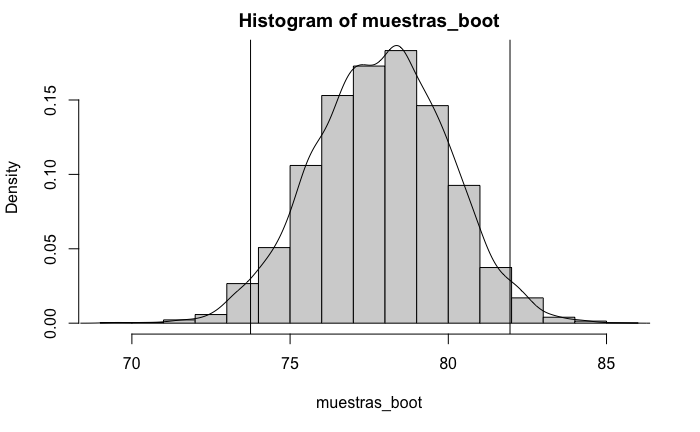
Figura 14.1: Distribución empírica de la media remuestreada.
El paquete boot de R permite también obtener réplicas de un estadístico sobre una muestra. La función básica de este paquete es boot(), que permite utilizar distintos métodos de remuestreo. En su estructura más simple, basta con indicar los datos originales, el estadístico que se quiere remuestrear y el número de réplicas.
Así, si se quiere estimar, por ejemplo, la mediana de la población con 1.000 remuestras, se puede recurrir a la función boot():
library(boot)
estadistico <- function(data, i) {
median(data[i]) # Se especifica aquí el estadístico remuestreado
}
set.seed(196)
mediana_boot <- boot(airquality$Temp, estadistico, R = 1000)
mediana_boot
#>
#> ORDINARY NONPARAMETRIC BOOTSTRAP
#>
#>
#> Call:
#> boot(data = airquality$Temp, statistic = estadistico, R = 1000)
#>
#>
#> Bootstrap Statistics :
#> original bias std. error
#> t1* 79 -0.052 1.071655Como resultado, se obtiene el valor del estadístico sobre la muestra original, el sesgo estimado y el error estándar.
Para calcular los intervalos de confianza, basta con utilizar la función boot.ci() sobre la muestra bootstrap obtenida, indicando el nivel de confianza y el tipo de intervalo (por defecto, all proporciona todos los intervalos disponibles; en el ejemplo, se usa el método de los percentiles)
boot.ci(mediana_boot, conf = 0.95, type = "perc")
#> BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
#> Based on 1000 bootstrap replicates
#>
#> CALL :
#> boot.ci(boot.out = mediana_boot, conf = 0.95, type = "perc")
#>
#> Intervals :
#> Level Percentile
#> 95% (77, 81 )
#> Calculations and Intervals on Original ScaleLa función boot() permite modificaciones del bootstrap uniforme mediante parámetros adicionales. Por ejemplo, el parámetro strata se utiliza para generar remuestreos estratificados cuando la muestra original también lo es. Aunque no se han comentado dado el carácter introductorio de este capítulo, existen otros métodos bootstrap, que se pueden obtener especificándolos mediante el parámetro sim. Por defecto, el valor es ordinary, que corresponde al bootstrap uniforme; otras alternativas pueden ser parametric para bootstrap paramétrico, balanced, permutation o antithetic para otros métodos más avanzados.
Resumen
El muestreo probabilístico busca seleccionar una muestra representativa de una población, que permita inferir la distribución poblacional o alguno de sus parámetros.
Las decisiones básicas para un correcto proceso de muestreo son el método utilizado (aleatorio simple, estratificado, polietápico, etc.), que depende de la estructura de la población, y la determinación del tamaño muestral que garantice el margen de error asumible.
La técnica bootstrap de remuestreo permite aproximar la distribución de estadísticos muestrales sin asumir ninguna hipótesis sobre la distribución poblacional, ventaja muy útil para evaluar la precisión de los estimadores en muchísimas técnicas complejas.