Capítulo 20 Modelización de series temporales

Mª Carmen García Centeno

Universidad San Pablo-CEU, CEU Universities

20.1 Conceptos básicos

El análisis de series temporales es muy útil para analizar el comportamiento de los datos con referencia temporal. Con dicho análisis, se trata de obtener modelos que expliquen su dinámica y puedan utilizarse para predecir valores futuros y tomar decisiones.

Una serie temporal se puede definir como el conjunto de valores observados, en períodos consecutivos de tiempo de la misma amplitud, de una característica de interés en la que su valor en cada instante temporal es una variable aleatoria. Por consiguiente, una serie temporal no es sino la realización de un proceso estocástico; por ejemplo: las precipitaciones diarias, la inflación mensual o el PIB trimestral.

A continuación se exponen algunos de los conceptos clave sobre los que se fundamenta el análisis de series temporales:

1. Proceso estocástico. Es una sucesión de variables aleatorias \(\{Y_t\}\), donde \(t= -\infty,..., -2, -1, 0, 1,2,...,\infty\), que dependen de un parámetro. En el caso de las series temporales ese parámetro es el tiempo.¹⁵¹ Así, en cada momento del tiempo el proceso se particulariza en una variable aleatoria con una determinada distribución de probabilidad. Desde el punto de vista práctico es muy complicado, y a veces imposible, caracterizar un proceso estocástico según su distribución de probabilidad conjunta. Por esta razón, se recurre a caracterizarlo de una forma menos completa, pero más sencilla y práctica, basada en los dos primeros momentos de una distribución; en concreto: la media (\(E(Y_t)=\mu_t\)), la varianza (\(Var(Y_t)=E(Y_t-\mu_t)^2=\sigma_t^2\)) y las covarianzas (\(\gamma(k)=Cov(Y_t,Y_{t-k})=E((Y_t-\mu_t)(Y_{t-k}-\mu_{t-k}))\)).

2. Estacionariedad. Un proceso estocástico es estacionario, en sentido simple o amplio, si su media y la varianza se mantienen invariantes a lo largo del tiempo y las covarianzas entre dos variables solo dependen del lapso de tiempo que transcurre entre ellas. Es decir:

3. Función de autocovarianzas. Está formada por el conjunto de autocovarianzas calculadas para distintos órdenes \((k)\). Tiene como finalidad determinar las relaciones de dependencia lineales que existen entre las variables del proceso con el fin de identificar el modelo que mejor explica su dinámica a lo largo del tiempo. 4. Función de autocorrelación simple (ACF). Está formada por el conjunto de coeficientes de correlación lineales calculados para distintos órdenes \((k)\). De forma genérica, para medir la correlación lineal existente entre \(Y_t\) e \(Y_{t-k}\), el coeficiente de correlación de orden \(k\), \(\rho(k)\), se calcula como el cociente entre la covarianza de y la varianza (ya que, como el proceso es estacionario, las desviaciones típicas de \(Y_t\) e \(Y_{t-k}\) son iguales).

\[\begin{equation} \rho(k) = \frac{Cov(Y_t,Y_{t-k})}{(\sqrt{ Var(Y_t)})(\sqrt {Var(Y_{t-k})})}=\frac{\gamma(k)}{\gamma(0)}. \end{equation}\]

La representación gráfica de los coeficientes de correlación \(\rho(k)\) para \(k=0,1,2,…\) se conoce como .

5. Función de autocorrelación parcial (PACF). Está formada por el conjunto de las correlaciones lineales parciales obtenidas para los distintos valores de \(k\). Así, para dos instantes de una serie temporal \(t\) y \((t-k)\), mide la correlación lineal existente entre las variables \(Y_{t}\) e \(Y_{t-k}\) asociadas a ellos, ajustada de los valores que toma el proceso temporal en los períodos intermedios (\(Y_{t-1},Y_{t-2},..., Y_{t-(k-1)}\)).¹⁵²

6. Ergodicidad. Un proceso estocástico es ergódico cuando, a partir de un determinado desfase temporal entre las variables, la correlación lineal existente entre ellas tiende a desaparecer. Esto implica que las covarianzas y el coeficiente de correlación tienden a cero, es decir,

\[\lim\limits_{k \to \infty}\gamma(k)=0 \quad y \quad \lim\limits_{k \to \infty}\rho(k)=0\]

7. Ruido blanco. Es un proceso puramente aleatorio que se puede expresar de la siguiente forma: \[Y_t=a_t.\] Se caracteriza por tener esperanza nula, varianza constante y covarianzas nulas. Es decir, \[E(a_t)=0 \quad\forall t; \quad E(a_t^2)=\sigma^2 \quad\forall t;\quad E(a_ta_s)=0 \quad\forall t\neq s.\] Esto implica que un proceso de ruido blanco siempre es estacionario.

20.2 Modelos ARIMA

Para determinar las características del proceso estocástico subyacente a la serie temporal, se van a utilizar los modelos ARIMA (acrónimo del inglés AutoRegresive Integrated Moving Average). Estos modelos están formados por tres componentes: AR (autorregresivo), I (integrado, es decir, número de diferencias necesarias para convertirlo en estacionario cuando no lo es) y MA (medias móviles). Fueron propuestos por Box y Jenkins y son un caso paraticular de procesos estocásticos lineales, estacionarios, ergódicos y discretos. Entre este tipo de procesos lineales, los más frecuentes son:

Los modelos ARIMA tratan de captar la dinámica y la dependencia existente en los datos de una serie temporal. Por lo tanto, son muy útiles para describir un valor como una combinación o función lineal de valores pasados y errores debidos al azar. Para detalles sobre la cuestión pueden verse, entre muchos otros, Hamilton (1994), Uriel Jiménez & Peiro Giménez (2000), Cryer & Chan (2010), Pemberton (2011), Mínguez Salido & García Centeno (2011), Brockwell & Davis (2016) y Shumway & Stoffer (2017).

En la modelización ARIMA se pueden destacar varias fases. La primera se centra en la identificación del modelo ARIMA que haya podido generar los datos de la serie temporal. En esta fase, es necesario decidir los órdenes del proceso (es decir, el desfase temporal entre el mayor y menor período de tiempo de las variables incluidas en el modelo) tanto de la parte regular como de la estacional.

La ACF y la PACF desempeñan un papel clave en la identificación de estos órdenes. Antes de calcular la ACF y la PACF, es necesario comprobar que la serie es estacionaria, es decir, que no deambula ni tiene tendencia creciente o decreciente. En el caso de que no lo sea, se realizarán las transformaciones necesarias para convertirla en estacionaria, ya que la modelización ARIMA exige que los datos sean estacionarios. Las dos razones fundamentales por las cuales pueden no ser estacionarios son: la no constancia en el tiempo de la media o la existencia de fluctuaciones de diferente amplitud que hacen que la varianza no se mantenga constante.

Si la serie no es estacionaria en varianza, de entre las transformaciones Box-Cox, se puede utilizar una transformación logarítmica porque reduce el rango dinámico de la variable, corrige la asimetría positiva y acerca a la normalidad la distribución de la variable; además, facilita la interpretación de las estimaciones de los coeficientes del modelo, ya que la diferencia del logaritmo de la serie es, aproximadamente, su tasa de variación porcentual.

Si no es estacionaria en media, puede ser debido a la existencia de tendencia en el tiempo o de estacionalidad. Para eliminar la tendencia se calculan las diferencias regulares (una o dos como máximo según el tipo de tendencia lineal o no lineal, es decir, \(Y_t-Y_{t-1}=\Delta Y_t\) o \(\Delta^2 Y_t=\Delta(\Delta Y_t)\), respectivamente). Para eliminar la estacionalidad, lo que se calcula es una diferencia estacional (es decir, \(Y_t-Y_{t-s}=\Delta_s Y_t\)).

Después de proponer el modelo, y tras dividir el conjunto de datos en dos subconjuntos (el de entrenamiento y el de test), se procede, con los datos del subconjunto apropiado, a la estimación del modelo, a su validación y a la realización de predicciones. Primero se obtienen las estimaciones de los parámetros del modelo propuesto, así como sus desviaciones típicas, y los residuos del modelo. Posteriormente, se aborda la fase de validación o diagnóstico y se realizan los contrastes necesarios para determinar si el modelo propuesto es adecuado o no, es decir, si los parámetros estimados son estadísticamente significativos o no; si el modelo estimado es estacionario e invertible; y si sus residuos siguen un proceso de ruido blanco o no. En el caso de que no lo sean, será necesario corregir el modelo con la información proporcionada por los residuos hasta obtener un modelo cuyos residuos sean ruido blanco. Finalmente, se procede a la utilización del modelo para predecir.

20.3 Análisis de series temporales con R

Algunas de las librerías que normalmente se suelen utilizar en la modelización de series temporales con R son:

library("tseries")
library("astsa")
library("forecast")
library("lubridate")
library("foreign")
library("quantmod")
library("ggplot2")

La libreria tseries permite manipular datos de series temporales; astsa es adecuada para analizar series de tiempo en los dominios de frecuencia y tiempo; forecast lleva a cabo (y analiza) predicciones con series temporales; lubridate facilita el trabajo con fechas y horas; foreign es esencial para crear objetos en R importando datos de casi cualquier formato conocido, como por ejemplo SAS, SPSS, Stata, etc.; quantmod ayuda, de forma cuantitativa, en el desarrollo de estrategias y modelización mediante la utilización de estadísticas; readxl facilita la exportación de datos de Excel a R; y ggplot2 es muy útil para la realización de gráficos.

En el caso real que se propone, se utilizan datos mensuales del INE (www.ine.es) correspondientes al índice general de precios al consumo (IPC) en el período muestral comprendido entre enero de 2002 y marzo de 2022. Los datos están en el fichero ipc del paquete CDR del libro.

ipc <- CDR::ipc

Para trabajar con series temporales, la fecha es un requisito imprescindible. En caso de que los datos no tuviesen fecha, habría que incluirla. Por ejemplo, para series mensuales, el código sería:

ipc_ts <- ts(ipc$ipc, start = c(2002, 1), end = c(2022, 3), frequency = 12)

En el caso del fichero ipc la fecha figura en la primera columna del fichero.

La representación gráfica de la serie original puede ayudar a saber si la serie ha sido generada por un proceso estacionario o no. Para obtener dicha representación, se ejecuta el siguiente código:

ipc$Time <- as.Date(ipc$Time)
ggplot(
  data = ipc,
  aes(x = Time, y = ipc)
) +
  theme(
    axis.title.x = element_text(size = 15),
    axis.title.y = element_text(size = 15)
  ) +
  geom_line(colour = "blue")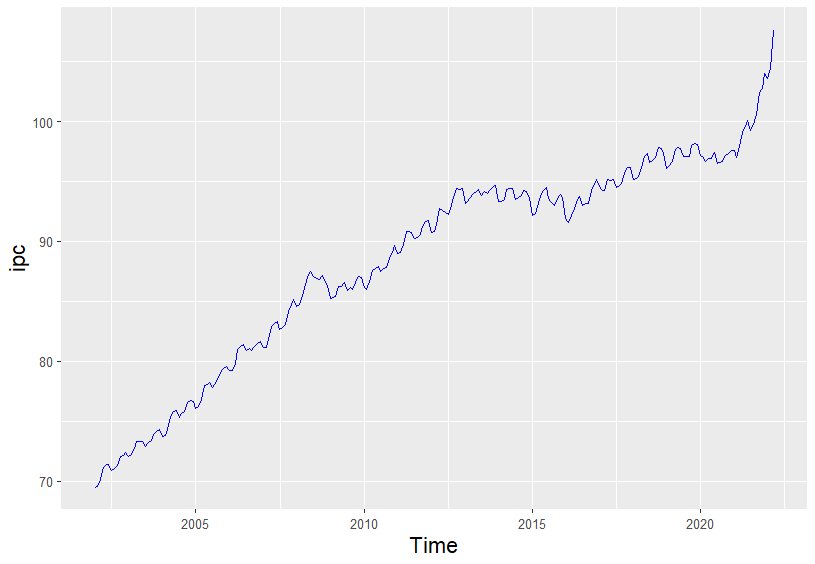

Figura 20.1: Evolución del IPC entre enero de 2002 y marzo de 2022.

La descomposición aditiva o multiplicativa en \((i)\) tendencia, \((ii)\) componente estacional, \((iii)\) componente cíclico y (\(iv\)) componente irregular de la serie del IPC, así como su representación gráfica, también puede ayudar a determinar si la serie es estacionaria o no. El código para la descomposición aditiva de la serie es el siguiente:

componentes_ts <- decompose(ipc_ts)
autoplot(componentes_ts)

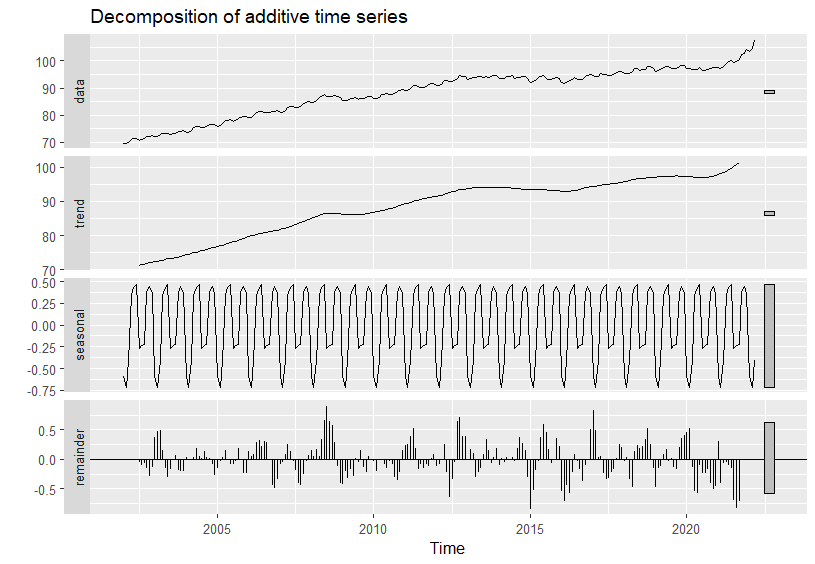
Figura 20.2: Descomposición aditiva del IPC.

Tanto en el gráfico de la serie original del IPC (Fig. 20.1) como en el de su descomposición en componentes (Fig. 20.2), se aprecia que la serie tiene tendencia y componente estacional (mensual). Por lo tanto, no es estacionaria en media, es decir, la media es distinta para diferentes meses y años; tampoco lo es en varianza, ya que la dispersión respecto de la media cambia a lo largo del tiempo.

Si una serie no es estacionaria ni en media ni en varianza es necesario empezar corrigiendo la no estacionariedad en varianza y, posteriormente, la no estacionariedad en media.

Las transformaciones de Box-Cox son las más utilizadas para corregir el problema de no estacionariedad en varianza. De todas estas transformaciones, la más habitual es el logaritmo. Para obtener la representación gráfica del logaritmo de \(Y_t\), se ejecuta el siguiente código:

logipc <- log10(ipc_ts)
ts_logipc <- data.frame(value = logipc, Time = time(logipc))
ggplot(
  data = ts_logipc,
  aes(x = Time, y = logipc)
) +
  theme(
    axis.title.x = element_text(size = 15),
    axis.title.y = element_text(size = 15)
  ) +
  geom_line(colour = "red")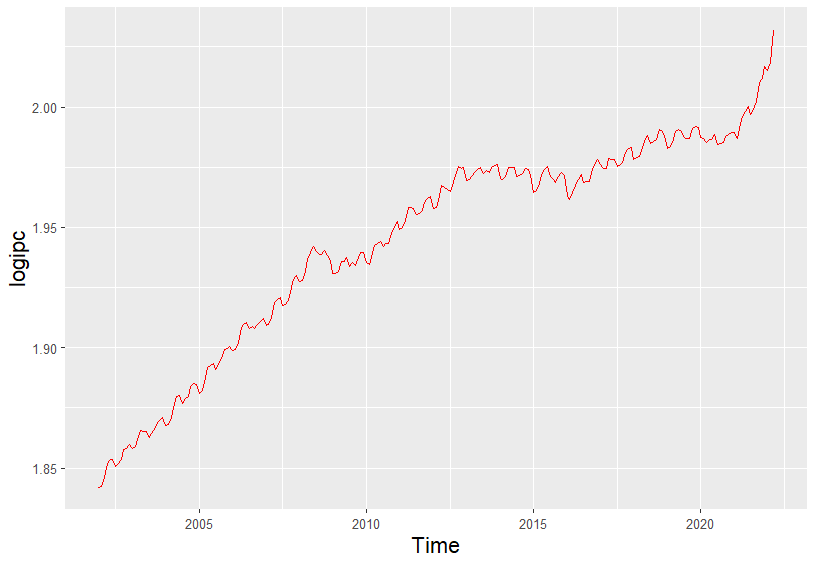

Figura 20.3: Logaritmo del IPC.

Corregido el problema de la no estacionariedad en varianza, en la Fig. 20.3 se aprecia que sigue sin ser estacionaria, ya que al tener estacionalidad y tendencia creciente no es estacionaria en media. Para conseguir que la serie sea estacionaria es necesario corregir tanto su tendencia como su estacionalidad.

Es indiferente cuál de los dos problemas se resuelve primero, pues el resultado final de la transformación es el mismo. En este caso, se empieza corrigiendo la tendencia. Para ello, se calcula una diferencia regular del logaritmo del IPC, obteniéndose la serie \((dlogipc_{t} = log(ipc_t) - log(ipc_{t-1})\). Al ser datos mensuales, esta transformación representa la tasa de variación relativa mensual del IPC. El código para calcular esta diferencia regular y su representación gráfica (Fig. 20.4) es:

dlogipc <- diff(logipc, differences = 1)
ts_dlogipc <- data.frame(value = dlogipc, Time = time(dlogipc))
ggplot(
  data = ts_dlogipc,
  aes(x = Time, y = dlogipc)
) +
  theme(
    axis.title.x = element_text(size = 15),
    axis.title.y = element_text(size = 15)
  ) +
  geom_line(colour = "blue")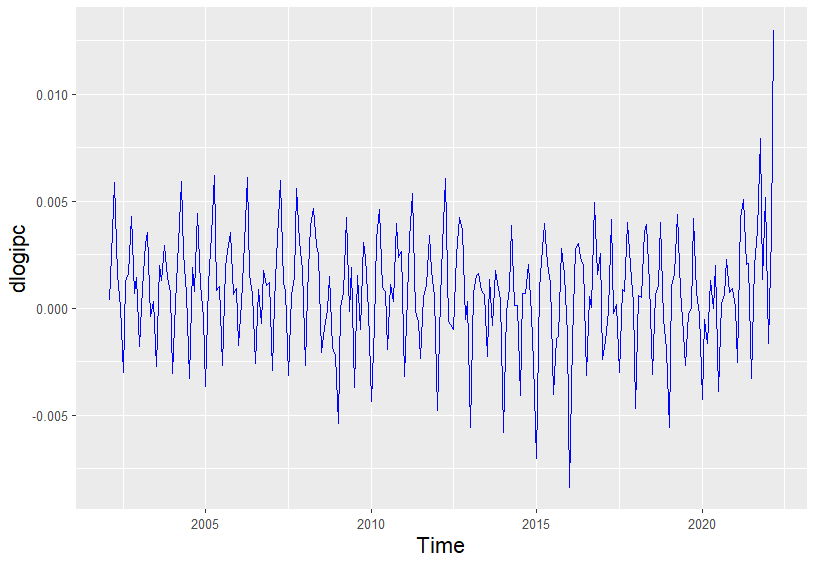

Figura 20.4: Diferencia regular del logaritmo del IPC.

Corregida la tendencia, a continuación se corrige su estacionalidad. Para ello, sobre la diferencia regular del logaritmo del IPC, se calculará una diferencia estacional mensual \((d12dlogipc_{t})= log(ipc_t) - log(ipc_{t-12})\). El código para calcular esta diferencia estacional y su representación gráfica (Fig. 20.5) es:

d12dlogipc <- diff(dlogipc, 12)
ts_d12dlogipc <- data.frame(value = d12dlogipc, Time = time(d12dlogipc))

ggplot(
  data = ts_d12dlogipc,
  aes(x = Time, y = d12dlogipc)
) +
  theme(
    axis.title.x = element_text(size = 15),
    axis.title.y = element_text(size = 15)
  ) +
  geom_line(colour = "purple")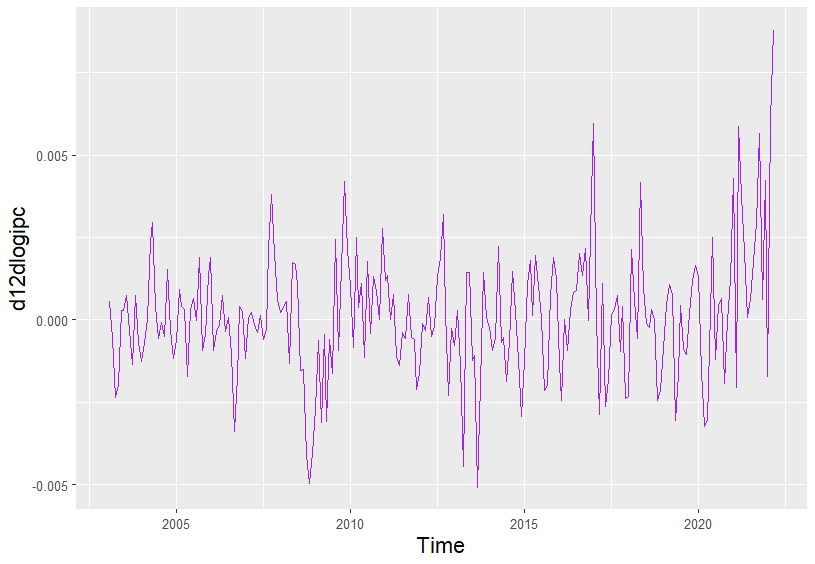

Figura 20.5: Diferencia estacional de la diferencia regular del logaritmo del IPC.

Para contrastar si una serie es estacionaria en media o no, también se puede utilizar un test de raíces unitarias.¹⁵³ A partir de la ecuación inicial de un AR: \[ \Delta Y_t=\alpha +(\phi-1)Y_{t-1}+a_t,\] las hipótesis del contraste son:

\[ H_0: (\phi-1)=0 \]

\[ H_1: (\phi-1)<0. \]

En esta ecuación se pueden añadir más retardos de la variable, una tendencia (en series que claramente tengan una tendencia decreciente o creciente) o eliminar la constante (en series con media nula). En este caso se utiliza el test de raíces unitarias de Dickey-Fuller, que es un test unilateral en el que la hipótesis nula es la existencia de raíces unitarias y, por lo tanto, que la serie no es estacionaria (es decir, es I(1)), mientras que la hipótesis alternativa es que sí es estacionaria (es decir, la serie es I(0)). Si se realiza el test sobre la serie original (ipc_ts) y sobre la serie transformada del IPC (d12dLogIPC), se comprueba que esta última es la transformación estacionaria. El código utilizado para realizar este contraste es:

adf.test(ipc_ts)
#>
#> Augmented Dickey-Fuller Test
#>
#> data: ipc_ts
#> Dickey-Fuller = -1.8396, Lag order = 6, p-value = 0.6433
#> alternative hypothesis: stationary
adf.test(d12dlogipc)
#>
#> Augmented Dickey-Fuller Test
#>
#> data: d12dlogipc
#> Dickey-Fuller = -3.3727, Lag order = 6, p-value = 0.06002
#> alternative hypothesis: stationary

A la luz del p–valor para los valores originales del IPC, si se preestablece un nivel de significación del 10%, no se rechaza la hipótesis nula (y, por tanto, la serie no es estacionaria). Sin embargo, para la serie resultante tras las transformaciones anteriores (d12dLogipc) se rechaza la \(H_0\). Siendo así, se puede concluir que dicha transformación la ha convertido en estacionaria.

20.3.1 Identificación o especificación del modelo

A partir de la transformación estacionaria del modelo es necesario calcular la ACF y la PACF muestrales, con el fin de identificar el modelo ARIMA más adecuado, es decir, especificar tanto el modelo como su correspondiente orden. Antes de hacerlo para el caso concreto del IPC, se analizan brevemente los principales modelos teóricos que pueden explicar la dinámica de una serie temporal. Estos modelos, para la parte regular (es decir, de la modelización de la dependencia asociada a observaciones consecutivas de tiempo) pueden ser: autorregresivos puros (AR(\(p\))), medias móviles (MA(\(q\))) o mixtos ARMA(\(p\), \(q\)), donde \(p\) y \(q\) representan sus correspondientes órdenes, respectivamente. En el caso de la parte estacional (\(s\)), es decir, de la modelización de la dependencia asociada a observaciones que distan entre sí \(s\)-períodos de tiempo o múltiplos de \(s\), se tiene: sAR(\(P\)), sMA(\(Q\)) o sARMA(\(P\), \(Q\)), donde \(P\) y \(Q\) representan, respectivamente, los órdenes de los modelos correspondientes a la parte estacional. Es necesario destacar que para identificar el modelo de la parte estacional es necesario analizar los coeficientes correspondientes a los retardos estacionales. Así, por ejemplo, en el caso de una serie mensual, habría que fijarse en los coeficientes correspondientes a los retardos 12, 24, 36, etc., para una serie trimestral, en los retardos, 4, 8, 12, 16, etc., y así sucesivamente.

Antes de identificar el modelo correspondiente al IPC en el período muestral analizado, se presentan algunos ejemplos de modelos ARIMA, su ecuación general y el comportamiento de su ACF y PACF.

• En el caso de MA(q) o sMA(Q):

  • La ACF se anula para órdenes superiores a q (o a Q en el caso estacional). Es decir, solo los q primeros coeficientes son significativos (o Q en el caso estacional). El resto de los coeficientes son nulos (o estadísticamente nulos en el caso muestral).

  • La PACF decrece de forma exponencial o sinusoidal hacia cero.

20.3.1.1 Ejemplo de las ACF y PACF teóricas de los procesos estacionarios MA(1)

La ecuación que describe la dinámica de un modelo MA(1) o ARMA(0, 1) es:

\[Y_t=a_t-\theta a_{t-1},\]

o bien, en forma polinómica:

\[Y_t=(1-\theta L)a_t , \]

donde \(L\) es el operador de retardos y \(a_t\) es un ruido blanco, es decir: \(E(a_t)=0 \; \;\forall t\); \(E(a_t^2)=\sigma^2 \; \; \forall t\); \(E(a_ta_s)=0 \quad\forall t\neq s\).

Este modelo siempre es estacionario (ya que se obtiene como una combinación de procesos de ruido blanco) y para que sea invertible (es decir, para que se pueda expresar en función del pasado de la variable), es necesario que las raíces del polinomio estén fuera del círculo unidad, o lo que es lo mismo, que \(|\theta|<1\).

Su ACF teórica es:

\[ \rho(k)=\left\{ \begin{array}{ll} \frac{-\theta}{(1+\theta^2)} & \text{si } k=1 \\ 0 & \text{}\forall k>1, \end{array} \right. \] y su PACF (también teórica) viene dada por: \[ \phi_{kk}=\frac{-\theta^k(1-\theta^2)}{1-\theta^{2(k+1)}}\quad \text {para} \quad k\geq 1. \]

• En un AR(p) o sAR(P):

  • La ACF decrece rápidamente de forma exponencial o sinusoidal hacia cero.

  • La PACF se anula para órdenes superiores a p (o a P, en el caso estacional). Es decir, solo los p (o P en el caso estacional) primeros coeficientes son significativamente distintos de cero. El resto de los coeficientes son nulos (o estadísticamente nulos en el caso muestral).

20.3.1.2 Ejemplo de las ACF y PACF teóricas de los procesos estacionarios AR(1)

La ecuación que describe la dinámica de un modelo AR(1) o ARMA(1, 0) es:

\[Y_t=\phi Y_{t-1}+ a_t,\]

o bien, en forma polinómica: \(Y_t(1-\phi L)=a_t\), donde \(L\) es el operador de retardos y \(a_t\) es un ruido blanco.

Este modelo siempre es invertible (ya que está expresado en función del pasado de la variable) y para que sea estacionario es necesario que las raíces del polinomio de retardos estén fuera del círculo unidad, o lo que es lo mismo, que \(|\phi|<1\).

Su ACF teórica es:

\[ \rho(k)=\phi\rho(k-1)=\phi^k, \]

mientras que su PACF (teórica) viene dada por:

\[ \phi_{kk}=\left\{ \begin{array}{ll} \rho_1=\phi & \text{si } k=1 \\ 0 & \text{}\forall k>1. \end{array} \right. \]

• En un ARMA(p, q) o sARMA(P, Q):

  • La ACF tiene un comportamiento irregular en los \(q\) primeros (o en los \(Q\) en el caso estacional) coeficientes. A partir del orden \(q\) (o \(Q\) en el caso estacional), se comporta como la de un AR(\(p\)) (o un sAR(\(P\)) en el caso estacional).

  • La PACF tiene un comportamiento irregular en los \(p\) primeros coeficientes (o \(P\) en el caso estacional). A partir del orden \(p\) (o \(P\) en el caso estacional), se comporta como la de un MA(\(q\)) (o de un sMA(\(Q\)) en el caso estacional).

20.3.1.3 Ejemplo de las ACF y PACF teóricas de los procesos estacionarios ARMA(1,1)

La ecuación que describe la dinámica de un modelo ARMA(1, 1) es:

\(Y_t=\phi Y_{t-1}+ a_t-\theta a_{t-1}\), o bien, en forma polinómica, \(Y_t(1-\phi L)=(1-\theta L)a_t\), donde \(L\) es el operador de retardos y \(a_t\) es un ruido blanco.

Para que el modelo sea estacionario, es necesario que las raíces del polinomio de la parte autorregresiva estén fuera del círculo unidad (es decir, que \(|\phi|<1\)).

Para que sea invertible es necesario que las raíces del polinomio de las medias móviles estén fuera del círculo unidad (o que \(|\theta |<1\)).

Además, es necesario que no existan raíces comunes, es decir, \(\phi \neq \theta\).

Su ACF teórica es:

\[ \rho(k)=\left\{ \begin{array}{ll} \frac{(1-\phi\theta)(\phi-\theta)}{1+\theta^2-2\phi\theta} & \text{si } k=1 \\ \phi\rho(k-1) & \text{}\forall k>1. \end{array} \right. \]

Su PACF teórica se obtiene como:

\[ \begin{array}{l} \phi_{11}=\rho_1 \\ \\ \phi_{22}=\frac{\begin{vmatrix} 1&\rho_1 \\ \rho_1 &\rho_2\end{vmatrix}}{{\begin{vmatrix} 1&\rho_1 \\ \rho_1 &1\end{vmatrix}}}=\frac{\rho_2-\rho_1^2}{1-\rho_1^2}\\ \\ \phi_{33}=\frac{\begin{vmatrix} 1&\rho_1&\rho_1 \\ \rho_1 &1&\rho_2\\\rho_2 &\rho_1&\rho_3\end{vmatrix}}{{\begin{vmatrix} 1&\rho_1&\rho_2 \\ \rho_1 &1&\rho_1\\\rho_2 &\rho_1&1 \end{vmatrix}}}=\frac{\rho_1^3-\rho_1\rho_2(2-\rho_2)+\rho_3(1-\rho_1^2)}{1-\rho_2^2-2\rho_1^2(1-\rho_2)}\\ \\ \vdots \end{array} \]

Nota:

La forma de obtener los diferentes coeficientes de la ACF y PACF de los modelos ARIMA estacionales es la misma que para los modelos ARIMA utilizados para la parte regular.

La diferencia fundamental reside en que para la parte regular se calculan los coeficientes de correlación entre las variables que se encuentran en períodos consecutivos de tiempo, mientras que para la parte estacional se hace entre las variables que están separadas entre sí \(s\) períodos o múltiplos de \(s\) (donde, por ejemplo, \(s=12\), si la serie es mensual; \(s=4\) si la serie fuese trimestral, etc.). Por esta razón, solo se muestra la forma de calcular la ACF y la PACF correspondiente a la parte regular.

Teniendo en cuenta lo anterior, en el caso concreto del IPC, después de obtener su transformación estacionaria, la ACF y la PACF muestrales son muy útiles para identificar el modelo ARIMA más adecuado, así como su correspondiente orden en el período muestral estudiado.

A continuación se muestra el código R para ejecutar los comandos que permiten calcular y representar la ACF y la PACF muestrales de la transformación estacionaria del IPC (Fig. 20.6 y Fig. 20.7, respectivamente). El número de retardos (\(lags\)) se establece en 40 para, así, incluir al menos 3 retardos estacionales (12, 24 y 36):

acf(ts(d12dlogipc, frequency = 1), lag.max = 40, main = "")

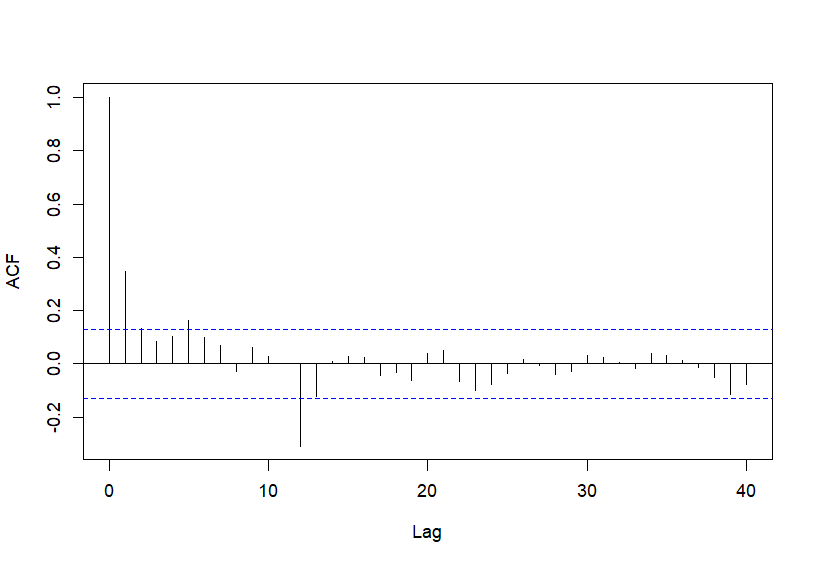
Figura 20.6: ACF. Función de autocorrelación muestral de \(d12dLogIPC\).

pacf(ts(d12dlogipc, frequency = 1), lag.max = 40, main = "")

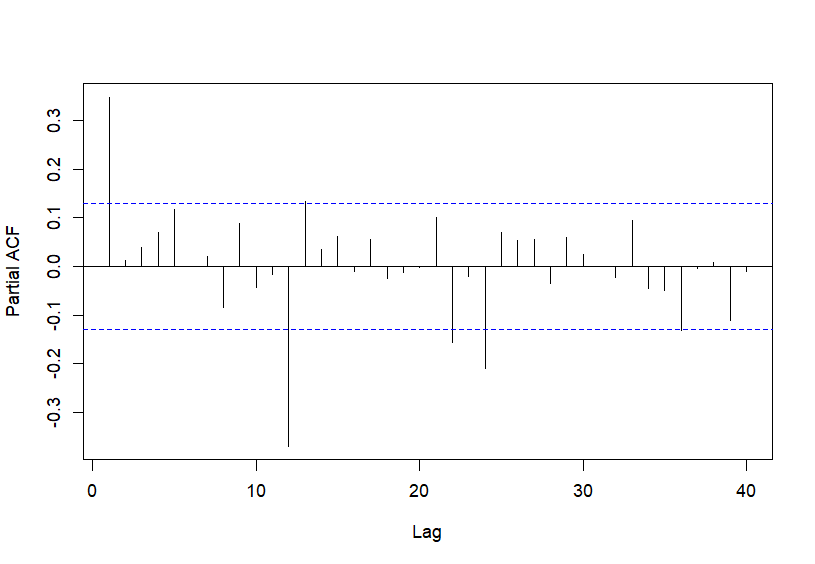
Figura 20.7: PACF. Función de autocorrelación parcial muestral de \(d12dLogIPC\).

Observando el comportamiento de estas funciones, para la parte regular se podría proponer un AR(1) y para la parte estacional un MA(1)12. Por lo tanto, ya que se ha calculado una diferencia regular y otra estacional para convertir a la serie original en estacionaria, el modelo ARIMA para el IPC, en el período muestral analizado, sería un ARIMA(1, 1, 0)(0, 1, 1) o sARIMA(1, 1, 0)(0, 1, 1). Cabe señalar que R permite la identificación automática de los órdenes del modelo.

20.3.2 Estimación del modelo

Los parámetros del modelo se estiman por el método de máxima verosimilitud. Dado que la función de máxima verosimilitud no es lineal, para maximizarla se lleva a cabo un procedimiento iterativo de estimación no lineal. El código en R que permite obtener las estimaciones de los parámetros del modelo y sus correspondientes desviaciones típicas es:

modelo <- arima(ipc_ts, c(1, 1, 0), c(0, 1, 1))
modelo
#>
#> Call:
#> arima(x = ipc_ts, order = c(1, 1, 0), seasonal = c(0, 1, 1))
#>
#> Coefficients:
#> ar1 sma1
#> 0.4665 -0.8302
#> s.e. 0.0701 0.0860
#>
#> sigmaˆ2 estimated as 0.1082: log likelihood = -77.76, aic = 161.51

20.3.3 Validación

En la metodología ARIMA desarrollada por Box y Jenkins es necesario determinar si el modelo propuesto es correcto o no, es decir, si se ajusta o no correctamente a los datos de la muestra. Para ello, en la fase de validación, fundamentalmente, es necesario comprobar que:

1. Los parámetros del modelo estimado cumplen con las condiciones de estacionariedad e invertibilidad.

El modelo estimado para el IPC es invertible y estacionario, ya que (i) la parte regular, al modelizarse mediante un AR(1), siempre va a ser invertible; además, dado que la estimación de \(\phi\) es, en valor absoluto, menor que uno, es decir, \(|0.4665| <1\), también es estacionario; (ii) la parte estacional sigue un esquema de medias móviles de primer orden (sMA(1)), que siempre es estacionario; como, adicionalmente, el valor absoluto de la estimación de \(\theta\) es menor que uno (\(|-0.8302|<1\)), también es invertible.

Si alguna de las raíces del polinomio de retardos de la parte autorregresiva estuviese próxima a uno, entonces es posible que la serie original este subdiferenciada y, por lo tanto, no sería estacionaria, lo que implicaría la necesidad de calcular alguna diferencia adicional. Si fuese alguna de las raíces del polinomio de retardos de las medias móviles la que estuviese próxima a uno, entonces el modelo podría estar sobrediferenciado y habría que eliminar alguna diferencia. Además, si existiesen raíces comunes en ambos polinomios de retardos de la parte regular, sería necesario eliminar diferencias tanto en la parte autorregresiva como en la parte de medias móviles y el modelo correcto sería un ARIMA(p-1, d, q-1). Los comentarios anteriores son válidos para la parte estacional.

2. Los parámetros estimados son estadísticamente significativos.

Para comprobar si los parámetros son estadísticamente significativos o no (o en otros términos, para comprobar si se ha sobreparametrizado o no el modelo), se realiza un contraste de significatividad individual para cada uno de ellos. Por ejemplo, para el parámetro del AR(1) la hipótesis nula y alternativa serían: \[ \begin{array}{l} H_0:\phi=0 \\ H_1:\phi\neq 0. \end{array} \]

Para realizar el contraste se utiliza el estadístico \(t\), que sigue una distribución \(t\)–Student con \((n-k)\) grados de libertad. Este estadístico \(t\) se calcula dividiendo el valor estimado del parámetro entre su correspondiente error estándar. En concreto, para los dos parámetros estimados de este modelo (el correspondiente al AR(1) de la parte regular y al sMA de la parte estacional) se tiene:

\[ t=\frac{0,4665}{0,0701} = 6,654 \quad y\quad |t|=|\frac{-0,8302}{0,0860}|=9,653. \]

Como, para un nivel de significación del 5% y 248 grados de libertad, el valor crítico de la \(t\)–Student es aproximadamente 1,96, se rechaza \(H_0\), lo que implica que las estimaciones de los dos parámetros del modelo son estadísticamente distintas de cero.

3. Los residuos del modelo son ruido blanco.

Como se avanzó al final de la Sec. 20.1, uno de los supuestos de la modelización ARIMA es que el error del modelo (o perturbación aleatoria) tiene que ser ruido blanco. Como los errores no son observables, las comprobaciones se llevan a cabo sobre los residuos (diferencia entre los valores reales y los predichos por el modelo). Existen varias formas de comprobar si los residuos son ruido blanco o no. Entre ellas, las más utilizadas son: el gráfico de la serie original de residuos, la ACF y la PACF estimadas y el contraste de Portmanteau (planteado inicialmente por Box-Pierce y actualizado posteriormente por Ljung-Box).

En primer lugar, de forma intuitiva, el gráfico de los residuos puede mostrar si la media es constante e igual a cero y si su varianza también es constante. Además, puede reflejar si existen valores atípicos u outliers (se consideran como tales aquellos que superen tres veces su desviación típica). El siguiente código R permite obtener los residuos y su representación gráfica (Fig. 20.8).

residuos <- residuals(modelo)
ts_residuos <- data.frame(value = residuos, Time = time(residuos))
ggplot(
  data = ts_residuos,
  aes(
    x = Time,
    y = residuos
  )
) +
  geom_line(colour = "red")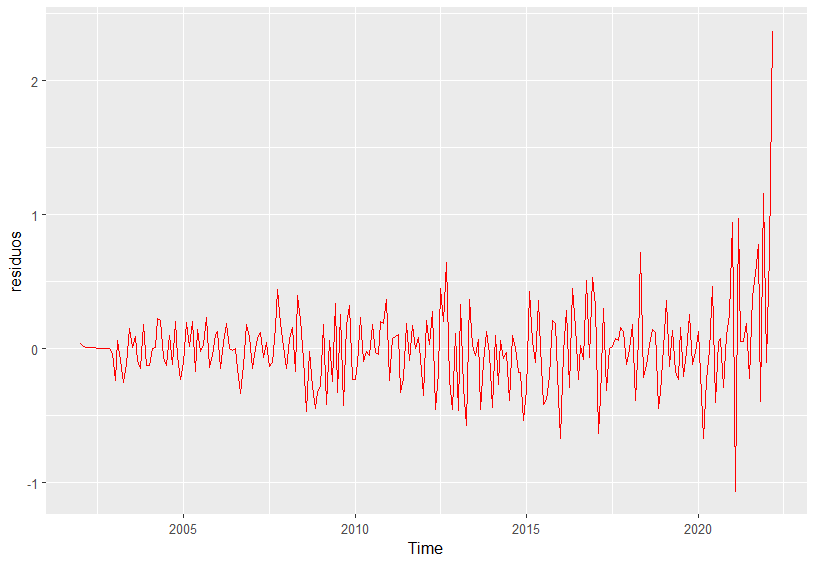

Figura 20.8: Gráfico de los residuos.

En la Fig. 20.8 se observa que la media es constante e igual a cero y que a partir de febrero de 2022, como consecuencia de las tensiones inflacionarias, los residuos son mayores que en el resto del período muestral.

En segundo lugar, se pueden calcular la ACF y la PACF muestrales de los residuos para comprobar que están incorrelacionados, es decir, que los coeficientes de correlación calculados son estadísticamente nulos. Si estos fuesen estadísticamente significativos, los residuos no serían ruido blanco. Entonces, para la correcta modelización habría que identificar el proceso e incorporarlo al modelo inicial propuesto para volver a estimarlo. Los correlogramas obtenidos con el código que se muestra a continuación (Fig. 20.9) indican que no hay coeficientes de correlación estadísticamente significativos (ya que se encuentran dentro de los intervalos de confianza) y, por lo tanto, los residuos son ruido blanco.¹⁵⁴

par(mfrow = c(2, 1), mar = c(1, 1, 1, 1) + 0.1)
acf(ts(residuos, frequency = 1), lag.max = 40)
pacf(ts(residuos, frequency = 1), lag.max = 40)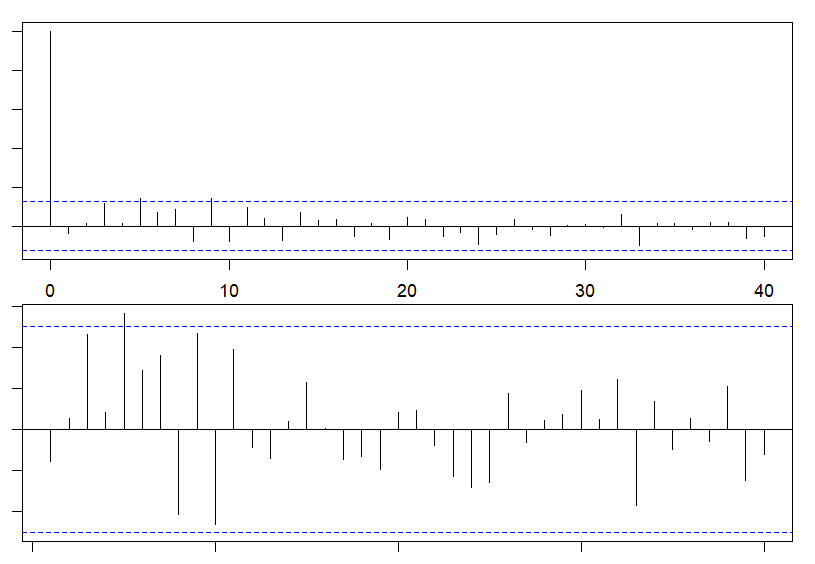

Figura 20.9: ACF y PACF estimadas de los residuos.

También se puede utilizar el contraste de Portmanteau (Ljung-Box) para comprobar si los residuos están incorrelacionados y se comportan como un ruido blanco o no. En este contraste global de significación, la hipótesis nula que se plantea, en el caso del IPC, es que los primeros 40 coeficientes de correlación son cero frente a la hipótesis alternativa de que no lo son. Para un nivel de significación del 5%, la evidencia empírica no es suficiente para rechazar \(H_0\), ya que el p–valor correspondiente al estadístico del contraste (Chi-cuadrado) es 0,5448, mayor que el nivel de significación del 5% y, por lo tanto, se concluye que los residuos están incorrelacionados. El código R para llevar a cabo el test de Box-Ljung es:

Box.test(residuos, type = "Ljung-Box")
#>
#> Box-Ljung test
#>
#> data: residuos
#> X-squared = 0.36682, df = 1, p-value = 0.5447

4. Análisis de la bondad del ajuste.

Finalmente, se debe comprobar la capacidad de ajuste del modelo comparando los valores observados y los estimados. Una forma sencilla e intuitiva de hacerlo es a través de su representación gráfica. El código R utilizado para ello es el siguiente:

plot(ipc_ts)
lines(ipc_ts - modelo$residuals, col = "red")

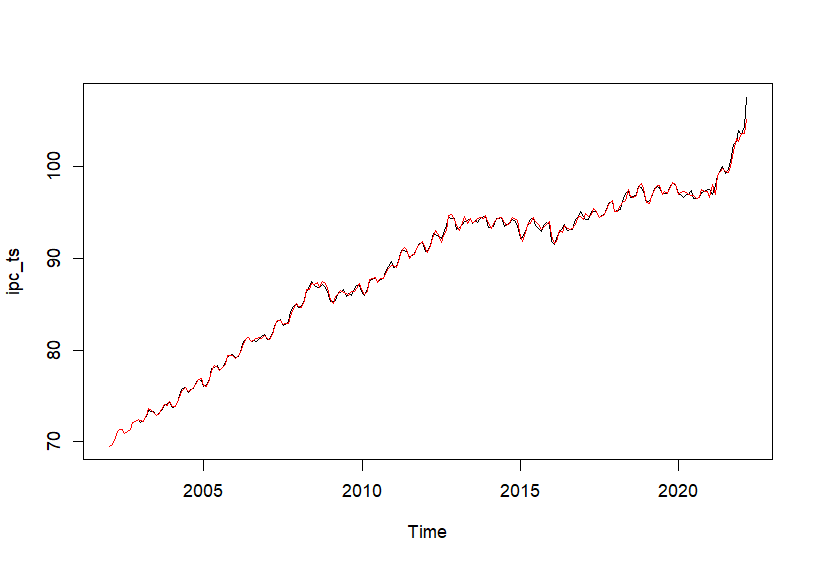
Figura 20.10: Ajuste con el modelo estimado.

La Fig. 20.10 muestra que el modelo estimado se ajusta bastante bien a los valores observados y, por lo tanto, evidencia que el modelo sARIMA (1, 1, 0)(0, 1, 1) propuesto capta la dinámica del IPC en el período muestral analizado.

Para comprobar la adecuación entre el modelo estimado y los valores observados no suele ser adecuado utilizar el coeficiente de determinación o el coeficiente de determinación corregido, ya que si hay que calcular diferencias para convertir la serie en estacionaria, la variable dependiente cambia (es decir, no es lo mismo \(Y_t\), que \(dlog(Y_t)\), que \(d12dlog(Y_t)\)). Si se quieren comparar diferentes modelos para elegir cuál es el que mejor se ajusta a los datos, hay que utilizar otros métodos de información, como el criterio de información de Akaike (AIC), el criterio bayesiano o de Schwarz (BIC) o el de Hannan-Quinn (HQC). Si, por ejemplo, se eligiese el AIC será mejor el modelo con menor AIC.

20.3.4 Predicción

Después de comprobar que el modelo ARIMA estimado es adecuado, se puede utilizar para obtener valores futuros de la variable objeto de análisis. Las predicciones que se obtienen pueden ser de dos tipos: puntuales o por intervalos. Las predicciones puntuales para un horizonte temporal h se obtienen calculando el valor esperado de la variable dependiente en \(T+h\) (\((Y_{T+h})\)) condicionado al conjunto de información disponible hasta el momento actual (\(T\)). Para obtener las predicciones por intervalos es necesario sumar y restar a la predicción puntual la desviación típica del error de predicción multiplicada por el valor crítico tabulado para el nivel de confianza fijado.

Algunas características generales de las prediciones obtenidas con modelos ARIMA son:

En el caso concreto del IPC, para obtener 12 predicciones puntuales y sus correspondientes intervalos de predicción al 80% y 95% de confianza, así como su representación gráfica (Fig. 20.11), el código R que hay que utilizar es:

forecast::forecast(modelo, h = 12)
#>    Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
#> Apr 2022 109.7116 109.2900 110.1332 109.0668 110.3564
#> May 2022 110.5926 109.8443 111.3410 109.4481 111.7371
#> Jun 2022 111.1030 110.0714 112.1346 109.5253 112.6806
#> Jul 2022 110.5518 109.2748 111.8289 108.5987 112.5050
#> Aug 2022 110.7714 109.2787 112.2641 108.4885 113.0543
#> Sep 2022 111.0288 109.3435 112.7140 108.4515 113.6060
#> Oct 2022 111.9631 110.1034 113.8228 109.1189 114.8073
#> Nov 2022 112.1740 110.1540 114.1939 109.0847 115.2632
#> Dec 2022 112.3896 110.2209 114.5583 109.0728 115.7064
#> Jan 2023 111.6049 109.2968 113.9130 108.0750 115.1349
#> Feb 2023 111.6666 109.2270 114.1061 107.9355 115.3976
#> Mar 2023 112.5012 109.9369 115.0656 108.5794 116.4231

predicciones <- forecast::forecast(modelo, h = 12)
autoplot(predicciones)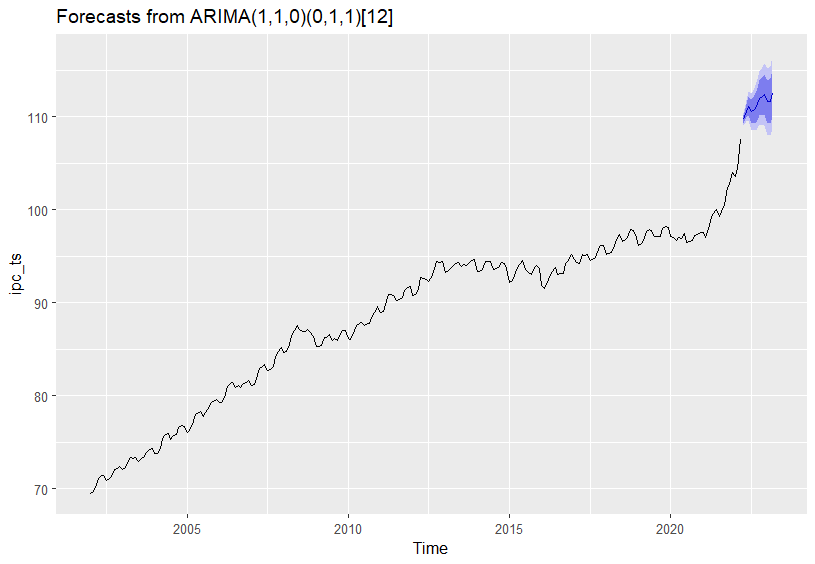

Figura 20.11: Predicciones con el modelo ARIMA(1, 1, 0)(0, 1, 1) estimado.

Resumen

Los modelos univariantes ARIMA analizan las series de tiempo desde un punto de vista moderno y estocástico y son muy útiles para captar su dinámica. Es importante destacar que:

• Hay que tener en cuenta conceptos básicos que son fundamentales para llevar a cabo una correcta modelización ARIMA. Entre ellos, se pueden destacar los siguientes: proceso estocástico, estacionalidad, estacionariedad, invertibilidad y ruido blanco.

• Las principales fases en el análisis de un modelo ARIMA son: especificación, estimación, validación y predicción.

• Para identificar el modelo ARIMA que mejor capta la dinámica de la serie temporal objeto de análisis, es necesario que los datos sean estacionarios en media y en varianza.

• La ACF y la PACF muestrales son muy útiles para identificar el modelo más adecuado para explicar la dinámica de los datos.

• Para comprobar que el modelo estimado es adecuado es necesario realizar un análisis de los parámetros estimados, un análisis de los residuos y medir la bondad del ajuste.

• Validado el modelo, se suele utilizar, fundamentalmente, para predecir y tomar decisiones.