Capítulo 22 Análisis conjunto

Mª Leticia Meseguer Santamaría

Universidad de Castilla-La Mancha

22.1 Introducción y conceptos clave

El análisis conjunto (o conjoint analysis) estudia situaciones de elección múltiple. Funciona dividiendo un producto o servicio en sus componentes (atributos y niveles) y analizando las utilidades parciales de cada uno; después se realizan diferentes combinaciones de estos para identificar las preferencias del consumidor. Permite conocer las preferencias del público ante el lanzamiento de nuevos productos o servicios, para adaptarlos a ellas y maximizar el éxito. Evalúa la sensibilidad al precio u otras características del producto y predice su comportamiento en el mercado. Mediante este análisis se puede establecer qué atributo y qué categoría (nivel) son los más valorados y cuantificarlos de forma relativa.

Los principales elementos de un análisis conjunto son:

• Atributos: características de un producto o servicio sobre las que se basará la elección.
• Niveles: valores que puede tomar cada atributo. El número de niveles no tiene por qué ser igual en todos los atributos, pero es conveniente que sea similar para facilitar la elección del entrevistado.
• Diseño experimental: proceso estadístico por el que se confeccionan las opciones de las preguntas de la encuesta, y que realiza el investigador.
• Utilidades parciales: valoración numérica que representa el grado de preferencia por cada nivel de atributo. Se hace en referencia a las otras opciones. También se conocen como “partworth utilities”, “niveles de preferencia”, “niveles relativos de preferencias” o “valoraciones relativas”.
• Importancia: valores numéricos que indican la preferencia por cada atributo.
• Perfil: combinación concreta de niveles de los atributos de un producto o servicio. También se denomina alternativa.
• Escenarios: conjunto de perfiles entre los que el entrevistado tiene que señalar sus preferencias.
• Pregunta: conjunto de opciones, normalmente entre 8 y 12.
• Probabilidad de elección: probabilidad de tomar una decisión determinada considerando las utilidades parciales.
• Modelo de comportamiento: modelo de decisión que se infiere a partir de las probabilidades de elección, después del análisis de las preferencias (utilidades parciales) de los entrevistados.
• Análisis: estimación de las utilidades parciales.
• Valoración: impacto del nuevo producto o servicio, basado en el modelo de comportamiento que se haya establecido.

Ejemplo: elección de gimnasio. Sea una muesta de gimnasios en la que se identifican 4 atributos (características) con distintos niveles. Se realiza una encuesta sobre qué gimnasio se prefiere. Los participantes eligen una opción entre las distintas combinaciones ofrecidas (preguntas). Mediante el análisis de los resultados de la encuesta se extrae el peso de cada atributo y nivel en las respuestas (utilidades parciales), que describen las preferencias medias de los encuestados; así mismo, se identifican los atributos y niveles más valorados y su importancia relativa.

Por ejemplo, los resultados pueden indicar que el horario más demandado es el de 09:00 a 23:00 durante 7 días a la semana (Fig. 22.1).

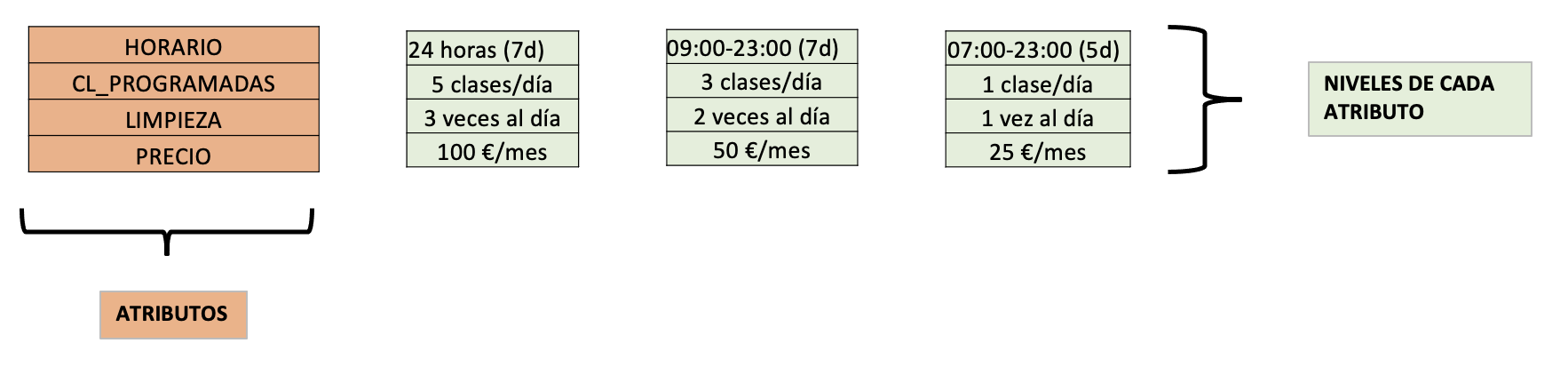
Figura 22.1: Elección de gimnasio. Atributos: horario, clases programadas, limpieza y precio.

22.2 Tipos de análisis conjunto

En la literatura científica sobre el análisis conjunto se diferencian tres formas de abordar la investigación:

El análisis tradicional de perfil completo (full profile)

Este análisis, también llamado conjoint value analysis (CVA), muestra al entrevistado una selección de productos resultantes de la combinación de determinados niveles de una serie de atributos (es decir, una serie de perfiles) y se le pide que los valore según su preferencia en una escala numérica (utilidad). Las preferencias globales de cada individuo se descomponen en utilidades independientes y compatibles para cada atributo y nivel mediante métodos basados en regresión lineal múltiple (véase Cap. 15), que proporcionan las utilidades para los distintos niveles, partworth utilities o, simplemente, partworths.

En el diseño original se detallan todos los perfiles hipotéticos (perfiles completos). Sin embargo, su número suele ser alto y se hace uso de técnicas de investigación que indiquen los más significativos. Está limitado a un análisis con muy pocos atributos y niveles.

El análisis conjunto adaptativo o adaptative conjoint analysis (ACA)

La recolección de datos se hace en dos fases: en la primera, el encuestado señala la importancia que le da a cada atributo; y en la segunda, asigna utilidades a un número limitado de perfiles. Es decir, se le conduce a través de una investigación sistemática por diferentes secciones, en las que se le presentan uno o pocos atributos, y que se va adaptando a sus respuestas. Se obtienen las valoraciones de los niveles de interés (utilidades parciales). Está limitado por su complejidad y por el uso de software especializado, aunque permite un gran número de atributos y niveles.

El análisis conjunto basado en elecciones o choice-based conjoint (CBC)

Pretende un mayor realismo, mostrando a cada entrevistado un grupo de productos distintos y se le pide que elija cuál de ellos prefiere. Además, contempla la posibilidad de no elegir ninguna alternativa. Las utilidades de los atributos-niveles se calculan mediante un modelo de regresión no lineal conocido como modelo de elección discreta. Sus principales inconvenientes son: \((i)\) tiene una mayor complejidad en su diseño y análisis, \((ii)\) requiere muestras muy grandes para tener validez estadística, y \((iii)\) el número máximo de atributos que admite es 10. Su mayor ventaja es que presenta un mejor sistema de elección que las alternativas anteriores.

22.3 Etapas de la realización del análisis conjunto

Para la aplicación correcta de un análisis conjunto es conveniente seguir una serie de etapas que faciliten las elecciones metodológicas que han de hacerse, así como la interpretación de los resultados.

Planteamiento del problema. Se analiza la oportunidad de aplicar esta técnica dados el objetivo y los datos del proyecto. Para ello, se debe especificar tanto el producto o servicio como los atributos que se quieren estudiar.

Elección de la metodología conjoint a aplicar. Esta dependerá, básicamente, de las características y cantidad de atributos estudiados; también se debe considerar la forma en que se valorarán por parte de los individuos. A modo de guía:

• Se opta por CVA cuando se analizan hasta 6 atributos, de productos o servicios habituales, de forma que el encuestado pueda hacer una elección rápida, sin demasiada reflexión.

• Se elige ACA cuando se analizan más de 10 atributos, procediendo de manera que la elección sea rápida pero reflexiva, ya que se trata de un proceso adaptativo cuyo resultado final depende, en buena medida, de la idoneidad de las primeras valoraciones.

• Se usa CBC si se analizan entre 6 y 10 atributos y con elecciones reflexivas sobre productos, puesto que el encuestado no asigna directamente utilidades, sino que se limita a elegir una (o ninguna) de las opciones presentadas.

La selección de elementos. Se escogen solo los atributos que condicionan la elección, es decir, los que expliquen las preferencias de los individuos y permitan diferenciar bien entre los productos o servicios; deben estar lo más cercanos posible a la independencia entre ellos. Para cada atributo se eligen sus niveles; deben ser mutuamente excluyentes y cubrir todo el rango de posibilidades. Por último, y dependiendo de la metodología utilizada, se determinan los perfiles y escenarios.

Creación de estímulos. Se utilizarán diseños factoriales fraccionados ortogonales, que reducen el número de perfiles que se le muestran al entrevistado. Como el número de posibles perfiles es la multiplicación del número de niveles de todos los atributos, puede ser imposible en la práctica que el individuo indique sus preferencias entre todos ellos. Por ello, se seleccionan solo algunos de los perfiles, que sean representativos del resto, es decir, que en los perfiles incluidos en los estímulos aparezca cada nivel de cada factor combinado con el resto de niveles de forma lo más proporcional posible.¹⁶⁶ La selección se efectúa mediante diseño factorial de experimentos, fraccionado (que jerarquiza los efectos, permitiendo la reducción de perfiles) y ortogonal (equilibrado en los niveles).

Forma de presentación. Dependerá de la metodología elegida. La Fig. 22.2 muestra algunos ejemplos.

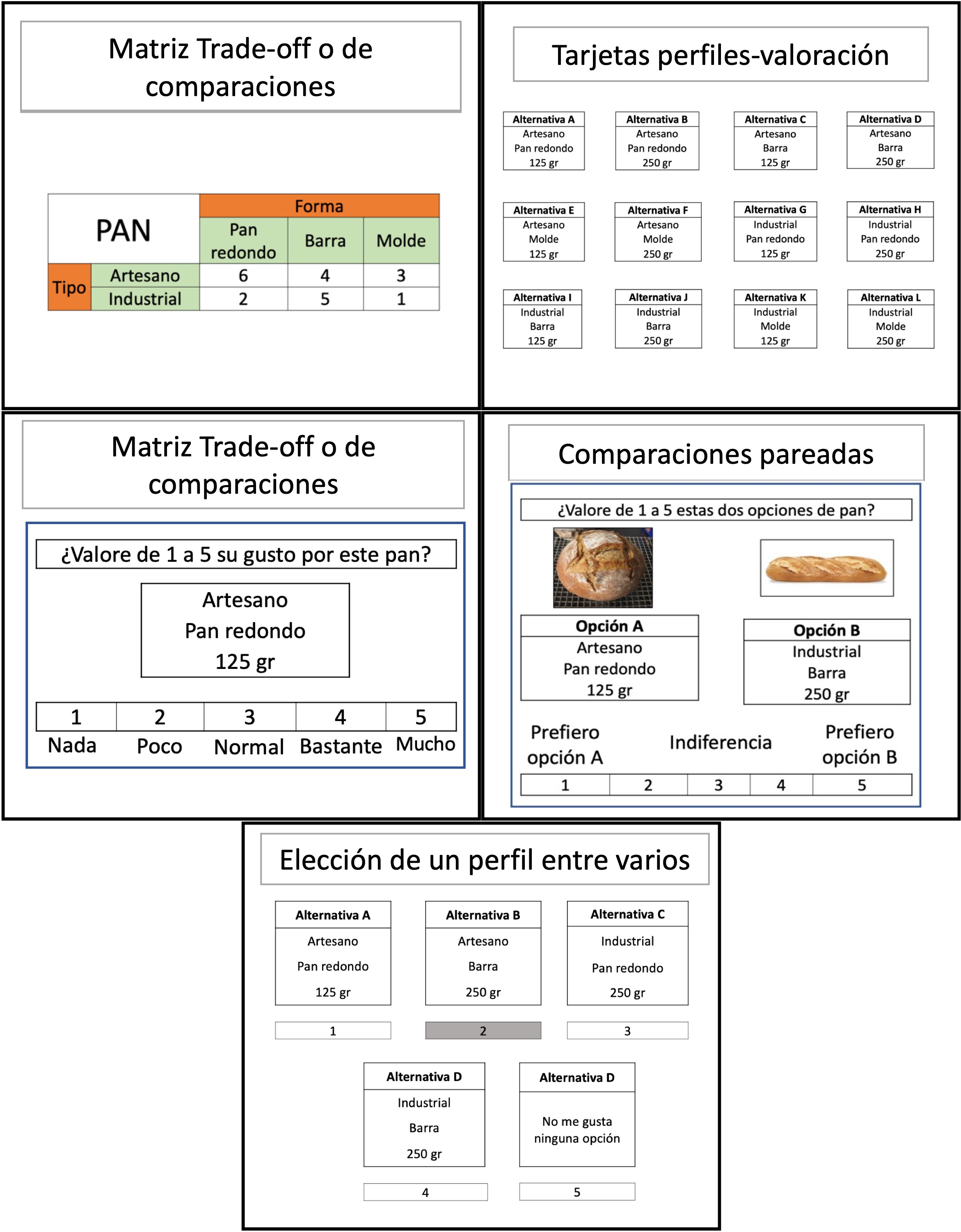
Figura 22.2: Formas de presentación.

• CVA: matriz de comparaciones o trade-off, en la que el entrevistado valora la combinación de atributos y niveles (solo es válida para dos atributos). Perfiles completos para ordenar, donde se elaboran perfiles de cada producto o servicio utilizando solo un nivel de cada atributo y el encuestado los valora (ordena) según sus preferencias. Perfil determinado para valorar, combinación que el encuestado valora según sus preferencias.

• ACA: comparaciones pareadas, en las que se comparan dos perfiles incompletos.

• CBC: elección de un perfil, en el que los encuestados señalan el perfil preferido entre el subconjunto que se les muestra, sin valorarlos ni ordenarlos.

Trabajo de campo y tratamiento de los datos

• CVA: la recogida de datos es en papel u ordenador, y el análisis en ordenador con software especializado.

• ACA y CBC: la recogida y el análisis son con ordenador.

Estimación de las utilidades

Con CVA se utiliza, por lo general, un modelo regresión por mínimos cuadrados ordinarios (OLS), mediante el cual se determinan las utilidades parciales o partworths, que indican las preferencias del encuestado mediante un modelo aditivo lineal en relación con los niveles de los atributos considerados como referencia.

Sea la variable \(X_{jk}^i\), que indica si el nivel \(k\) del j-ésimo atributo está o no en el i-ésimo perfil. Dicha variable toma solo los valores \(X_{jk}^i=1\) (si está) y \(X_{jk}^i=0\) si no lo está. Sea \(Y^{i}\) la preferencia que tiene un individuo sobre el i-ésimo perfil. Entonces la función de utilidad a estimar es:

\[\begin{equation} \tag{22.1} Y^{i}=\beta_0 + \sum_{j,k} U_{jk} X_{jk}^{i} + \varepsilon^{i}, \end{equation}\]

donde los coeficientes \(U_{jk}\) son las utilidades parciales, o partial partworths, que indican la utilidad que el individuo asigna a cada nivel de cada atributo, y \(\varepsilon^{i}\) denota el término de error.

En el modelo (22.1) habrá multicolinealidad,¹⁶⁷ ya que todos los atributos deben estar presentes en todos los perfiles, es decir, \(\sum_k X_{jk}^{i}=1\). Para evitar las consecuencias indeseadas de la multicolinealidad en la estimación de las utilidades parciales, se elimina uno de los niveles de cada factor (sin pérdida de generalidad, el último, \(K\)), estimándose por OLS la función de utilidad (que ahora se denomina “restringida”):

\[\begin{equation} \tag{22.2} Y^{i}=\delta + \sum_{j,k, k \neq K} \gamma_{jk} X_{jk}^{i} + \varepsilon^{i}, \end{equation}\]

donde \(\delta = \beta_0 + \sum_{j} U_{jK}\) y \(\gamma_{jk}=U_{jk}-U_{jK}\). A partir de la estimación de (22.2), se pueden calcular los valores de la función de utilidad original en (22.1).¹⁶⁸

Si hay \(Z\) individuos, cada uno de ellos, \(z\), dará una valoración diferente a los perfiles \(i\), es decir, los valores de \(Y_{z}^{i}\) serán diferentes, produciendo una estimación diferente de la función de utilidad (22.1) y, por tanto, diferentes utilidades parciales \(\widehat{U}_{jk,z}\). Para obtener las utilidades para el conjunto de individuos, se procede al cálculo de sus valores medios:

\[\begin{equation} \tag{22.3} \widehat{U}_{jk} = \frac{\sum_{z} \widehat{U}_{jk,z}}{Z}. \end{equation}\]

Se obtienen, así, las utilidades de cada nivel \(k\) de cada atributo \(j\), reflejando la importancia que conceden los individuos a cada uno de esos niveles.

Para determinar la importancia de cada atributo \(j\) se utiliza la diferencia entre la utilidad más alta y más baja de sus niveles, es decir:

\[\begin{equation} \tag{22.4} Imp_{j}=\max_{k} \lbrace {U_{jk}} \rbrace - \min_{k} \lbrace {U_{jk}} \rbrace . \end{equation}\]

En términos relativos, la importancia de cada atributo \(j\) respecto al conjunto de atributos se puede expresar como:

\[\begin{equation} \tag{22.5} ImpRel_{j}=\frac{Imp_{j}}{\sum_{t=1}^{J} Imp_{t}}. \end{equation}\]

Por último, una vez estimadas las utilidades, la utilidad total de un perfil \(i\) es la suma de las utilidades de los niveles de cada uno de los atributos que lo definen más la constante de regresión:¹⁶⁹

\[\begin{equation} \tag{22.6} \widehat{U}_i=\beta_0 + \sum_{j=1}^J\widehat{U}_{jk}\hspace{0,2cm} \text{para los niveles presentes en el perfil}, \end{equation}\]

donde: \(\widehat{U}_i\) es la utilidad total del perfil \(i\); \(\widehat{U}_{jk}\) es la utilidad parcial asociada con el nivel \(k\) del atributo \(j\); y \(\beta_0\) es la constante de regresión.

En los casos de las metodologías ACA y CBC, la estimación de las utilidades parciales es más compleja, debiendo recurrir a modelos de regresión no lineal. Sin embargo, su interpretación es la misma que en el caso de la metodología CVA.

Interpretación de resultados. Algunos de los resultados del análisis conjunto que frecuentemente se analizan son:

• La importancia de los atributos y niveles. La importancia relativa de cada atributo (\(ImpRel_{j}\)) refleja la opinión de los individuos sobre la relevancia (en porcentaje) de dichos atributos a la hora de evaluar los perfiles. Igualmente, para cada atributo \(j\), las utilidades de sus niveles \(U_{jk}\) muestran la importancia relativa asignada a dichos niveles en la valoración de cada atributo.

• Las utilidades totales de cada perfil, o la comparación relativa entre un conjunto determinado de perfiles, permiten detectar cuáles son los preferidos por los individuos. Esta información puede orientar en la determinación de la configuración final del producto o servicio analizado.

• La influencia de un determinado atributo sobre la elección de los individuos. Así, es posible estimar el cambio en la utilidad que se produciría por la modificación de sus niveles (cambio generalmente conocido como elasticidad); por ejemplo, si un atributo fuese el precio, se podría dar una aproximación a la variación de utilidad producida por un incremento del precio.

• Al disponer de las utilidades parciales de cada individuo, es posible estudiar si estas son homogéneas para toda la muestra o si, por el contrario, existen grupos de individuos con utilidades parecidas entre ellos y diferenciadas del resto. Este planteamiento podría ayudar a segmentar el mercado y a ofrecer productos o servicios diferenciados a cada nicho de mercado.

22.4 Procedimiento con R: la función Conjoint()

Para ejemplificar la puesta en práctica del análisis conjunto, con el método de perfil completo (CVA), se utiliza el paquete conjoint y su base de datos tea, compuesta por 5 listados: niveles (tlevn), perfiles (tprof), preferencias (tpref), preferencias en forma matricial (tprefm) y la simulación de perfiles (tsimp).

El listado tprof recoge los 13 perfiles que se presentan a los individuos, cada uno de ellos con una combinación de niveles de cada factor. El hecho de utilizar un diseño factorial fraccionario ortogonal ha permitido encontrar una muestra de perfiles representativa del total (habría \(3 \cdot 3 \cdot 3 \cdot 2=54\) perfiles distintos) donde cada nivel de cada atributo está representado, aproximadamente, de forma proporcional.

La matriz tprefm contiene las preferencias que cada uno de los 100 individuos asigna a cada uno de los perfiles \(i\) que se le presentan (estas preferencias se recogen ordenadas en el vector tpref). Por último, tsimp muestra cuatro simulaciones de perfiles distintos a los mostrados a los individuos.

En este ejemplo, se desea conocer el por qué unos tés son preferidos a otros. Para ello, en el contexto de un análisis tradicional con perfiles incompletos, se seleccionan 4 atributos, con sus correspondiente niveles (tlevn):

• Precio, distinguiendo entre bajo, medio y alto.

• Variedad, distinguiendo entre negro, verde y rojo.

• Forma de presentación, distinguiendo entre bolsita, granulado y hojas.

• Aroma, distinguiendo entre aromático y no aromático.

De las 54 posibles combinaciones se seleccionan 13 perfiles, valorados de 0 a 10 según las preferencias de cada uno de los 100 encuestados.

Para realizar el análisis conjunto propuesto, primeramente se carga tanto el paquete como los datos:

library("conjoint")
data("tea")

La función Conjoint() devolverá las utilidades de los niveles, el vector de porcentajes de la importancia de los atributos y las gráficas correspondientes.¹⁷⁰

Conjoint(y=tpref, x=tprof, z=tlevn)

En la Tabla 22.1 se exponen otras funciones disponibles para obtener algunos resultados concretos:

Tabla 22.1: Funciones en R para cálculos sobre análisis conjunto

Función en R	Utilidad-resultado
caUtilities(y=tprefm , x=tprof, z=tlevn)	Utilidades medias para cada nivel
caPartUtilities(y=tprefm , x=tprof, z=tlevn)	Matriz de utilidades de los niveles para cada individuo
caTotalUtilities(y=tprefm , x=tprof)	Utilidades totales de los perfiles mostrados para cada individuo
colMeans(caTotalUtilities(y=tprefm , x=tprof))	Utilidades totales medias para cada perfil
ShowAllUtilities(y=tprefm , x=tprof, z=tlevn)	Todas las utilidades
caImportance(y=tprefm , x=tprof)	Importancia relativa media de cada atributo
caModel(y=tprefm[20,], x=tprof)	Utilidades para un solo individuo, por ejemplo, el 20

Así, es posible obtener solo la información relativa a las utilidades, mediante la función caUtilities(), o solo la correspondiente a la importancia de los atributos, usando la función caImportance():

caUtilities(y=tprefm , x=tprof, z=tlevn)
#> 
#> Call:
#> lm(formula = frml)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -5,1888 -2,3761 -0,7512  2,2128  7,5134 
#> 
#> Coefficients:
#>                    Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)         3,55336    0,09068  39,184  < 2e-16 ***
#> factor(x$price)1    0,24023    0,13245   1,814    0,070 .  
#> factor(x$price)2   -0,14311    0,11485  -1,246    0,213    
#> factor(x$variety)1  0,61489    0,11485   5,354 1,02e-07 ***
#> factor(x$variety)2  0,03489    0,11485   0,304    0,761    
#> factor(x$kind)1     0,13689    0,11485   1,192    0,234    
#> factor(x$kind)2    -0,88977    0,13245  -6,718 2,76e-11 ***
#> factor(x$aroma)1    0,41078    0,08492   4,837 1,48e-06 ***
#> ---
#> Signif. codes:  0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1
#> 
#> Residual standard error: 2,967 on 1292 degrees of freedom
#> Multiple R-squared:  0,09003,    Adjusted R-squared:  0,0851 
#> F-statistic: 18,26 on 7 and 1292 DF,  p-value: < 2,2e-16
#>  [1]  3.55336207  0.24022989 -0.14311494 -0.09711494  0.61488506  0.03488506
#>  [7] -0.64977011  0.13688506 -0.88977011  0.75288506  0.41077586 -0.41077586
caImportance(y=tprefm , x=tprof)
#> [1] 24.76 32.22 27.15 15.88

Interpretación del resultado

• La primera parte de la salida corresponde a los coeficientes del modelo de regresión (22.2), donde no se incluye el último nivel de cada atributo (para evitar la multicolinealidad); se señalan con asteriscos los que resultan estadísticamente significativos. También se indica el grado de ajuste del modelo. A continuación, están las utilidades parciales para todos los niveles de todos los atributos:

• El primer valor (3,5534) corresponde al término independiente del modelo, por lo que no está asociado a ningún atributo.

• Para el atributo precio, es el nivel bajo (low) el que recibe mayor preferencia (0,2402), siendo el nivel medio (medium) el menos preferido (-0,1431), algo por debajo de la preferencia del nivel alto (high), -0,0971.

• Para el atributo variedad, el té negro (black) es el nivel con mayor utilidad (0.6149), seguido del té verde (0,0349), quedando el nivel de té rojo con una preferencia mucho menor (-0,6498).

• En el caso del atributo presentación, en hojas (leafy) es el nivel más preferido (0,7529), seguido de la modalidad en bolsitas (bags), con una utilidad de 0.1369; el nivel granulado presenta la preferencia más baja (-0,8898).

• Por último, para el atributo aroma, que sea aromático (yes) es el nivel más preferido, con una utilidad de 0,4108; al ser un atributo con solo dos niveles, la preferencia del otro nivel (no) es -0,4108.

La última parte de la salida recoge la importancia relativa de cada atributo, calculada a partir de la importancia de cada atributo (22.4) pero expresada como proporción de la suma de importancias de todos ellos (22.5).

En este ejemplo, el atributo con más peso es la variedad de té, con una importancia relativa del 32,22%; el siguiente es la presentación, con un 27,15%; después, el precio, con un 24,76%; y por último, el aroma, con un 15,88%. Es decir, el conjunto de 100 individuos, al valorar los perfiles que se les presentan, consideran principalmente el atributo variedad, seguido de forma de presentación y precio; por el contrario, que sea aromático o no aporta relativamente poca valoración.

De forma adicional, el análisis conjunto también permite profundizar en el conocimiento de los individuos en función de sus preferencias. Como ejemplo, se puede abordar la cuestión de si existen grupos de individuos con preferencias similares entre ellos y diferentes de las del resto de grupos, cuestión conocida generalmente como segmentación. En este caso, el objetivo del proyecto sería identificar grupos de encuestados con preferencias similares, segmentando el mercado y permitiendo adaptar los atributos de cada producto o servicio a las características concretas de ese nicho de mercado.

Para ello, se puede utilizar la función caSegmentation(), que devuelve un análisis de conglomerados dividiendo a los individuos en \(k\) clústeres, usando el método k-means (véase Sec. 31). Como ejemplo, se consideran tres clústeres.

El vector de agrupación resume las características de los tres grupos formados.

segments<-caSegmentation(y=tprefm , x=tprof, c=3)
segments$segm
#> K-means clustering with 3 clusters of sizes 40, 40, 20
#> 
#> Cluster means:
#>       [,1]   [,2]   [,3]     [,4]   [,5]     [,6]     [,7]     [,8]     [,9]
#> 1 5.480275 2.9381 1.3681 4.540275 1.9731 3.782900 1.382900 0.965750 2.820750
#> 2 4.754975 4.6918 3.6718 6.964975 6.6918 3.500525 4.385525 2.717225 3.062225
#> 3 2.623500 6.6211 4.7511 2.933500 2.5211 4.189050 4.549050 5.066950 2.086950
#>      [,10]    [,11]    [,12]    [,13]
#> 1 0.111225 3.450750 0.442900 0.692900
#> 2 1.840925 6.292225 6.595525 7.105525
#> 3 5.312100 4.266950 4.859050 3.569050
#> 
#> Clustering vector:
#>   [1] 2 3 2 2 2 1 2 3 2 2 2 2 1 1 1 1 3 1 3 1 1 2 1 2 3 2 3 3 2 2 1 2 3 2 2 2 2
#>  [38] 1 1 1 1 3 1 3 1 2 2 1 1 1 2 1 1 1 2 2 1 2 1 3 1 1 2 3 3 2 1 1 1 2 2 1 2 3
#>  [75] 2 2 2 1 2 2 3 3 2 2 1 1 1 1 3 1 3 1 3 1 1 2 1 3 2 2
#> 
#> Within cluster sum of squares by cluster:
#> [1] 1605.654 2690.267 1131.293
#>  (between_SS / total_SS =  41.4 %)
#> 
#> Available components:
#> 
#> [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
#> [6] "betweenss"    "size"         "iter"         "ifault"

La salida contiene, en el apartado Cluster means, las utilidades medias de cada nivel (recogidas en las 13 columnas) para cada uno de los tres grupos (en filas), mostrando las diferencias entre ellas. La composición de cada clúster se muestra en el apartado Clustering vector, que recoge el clúster de pertenencia de cada uno de los cien individuos.

Resumen

• El análisis conjunto estudia situaciones de elección múltiple.

• Divide un producto o servicio en atributos y niveles y analiza las utilidades parciales de cada uno; después, se realizan diferentes combinaciones de estos para identificar las preferencias del consumidor, estableciendo qué atributos y niveles son los más valorados, cuantificando dicha valoración de forma relativa.

• Permite evaluar las preferencias del público ante el lanzamiento de nuevos productos o su sensibilidad ante alguna característica, como el precio, el formato, cambios en la imagen del producto, etc.