Capítulo 31 Análisis clúster: clusterización no jerárquica

José-María Montero\(^{a}\) y Gema Fernández-Avilés\(^{a}\)

\(^{a}\)Universidad de Castilla-La Mancha

31.1 Introducción

Como se avanzó en la Sec. 30.4.1, aunque las técnicas de agrupación jerárquicas son muy utilizadas, existen otras, también muy populares, que se aglutinan bajo la denominación de no jerárquicas y que se pueden clasificar, sin ánimo de exhaustividad, en \((i)\) de optimización o reasignación; \((ii)\) basadas en la densidad de elementos; y \((iii)\) otras, como los métodos directos (por ejemplo, el block-; bi-; co-; two-mode clustering), los de reducción de la dimensionalidad (como el Q- y el R-factorial), los métodos de clusterización difusa, o los basados en mixturas de modelos.

Las técnicas no jerárquicas proceden con el criterio de la inercia, maximizando la varianza intergrupos y minimizando la intragrupos. Se caracterizan porque:

• El número de clústeres se suele determinar a priori.
• Utilizan directamente los datos originales, sin necesidad de cómputo de una matriz de distancias o similaridades.
• Los elementos pueden cambiar de clúster.
• Los clústeres resultantes no están anidados unos en otros.

31.2 Métodos de reasignación

Los métodos de reasignación permiten que un elemento asignado a un grupo en una determinada etapa del proceso de clusterización sea reasignado a otro grupo, en una etapa posterior, si dicha reasignación implica la optimización del criterio de selección. El proceso finaliza cuando no hay ningún elemento cuya reasignación permita optimizar el resultado conseguido. Estas técnicas suelen asumir un número determinado de clústeres a priori y se diferencian entre sí en la manera de obtener la partición inicial y en la medida a optimizar en el proceso. Respecto a esta última cuestión, los procedimientos más populares son: \((i)\) la minimización de la traza de la matriz de covarianzas intragrupos; \((ii)\) la minimización de su determinante; \((iii)\) la maximización de la traza del producto de las matrices de covarianzas intergrupos e intragrupos; y \((iv)\) medidas de información o de estabilidad.

31.2.1 Técnicas basadas en centroides: métodos de Forgy y \(k\)-medias

Los algoritmos de reasignación más populares son el de Forgy y, sobre todo, el \(k\)-medias. La literatura sobre este tipo de técnicas no es clara y, frecuentemente, se confunden el método de Forgy y el \(k\)-medias, así como el \(k\)-medias con algunas de sus otras denominaciones (dándose a entender que son técnicas distintas). Sin embargo, la historia es la siguiente: originalmente, Forgy (1965) propuso un algoritmo consistente en la iteración sucesiva, hasta obtener convergencia, de las dos operaciones siguientes: \((i)\) representación de los grupos por sus centroides; y \((ii)\) asignación de los elementos al grupo con el centroide más cercano. Posteriormente, Diday (1971), Diday (1973), Anderberg (1973), Bock (1974) y Späth (1975) desarrollaron una variante del método de Forgy que solo se diferencia de él en que los centroides se recalculan después de asignar cada elemento (con la técnica de Forgy primero se llevan a cabo todas las asignaciones y posteriormente se recalculan los centroides). Diday la llamó método de las nubes dinámicas o clústeres dinámicos, Anderberg se refirió a ella como el criterio de inclusión en el grupo del centroide más cercano, Bock la denominó particionamiento iterativo basado en la mínima distancia y Späth la llamó HMEANS, una versión por lotes del procedimiento de los autores anteriores. Sin embargo, fue MacQueen (1967) quien previamente acuñó la denominación de “\(k\)-medias” que se usa hasta la fecha.

\(K\)-medias²¹⁰ requiere la especificación previa del número de grupos, \(k\), en los que se va a dividir el conjunto de elementos. El algoritmo:

1. Selecciona \(k\) elementos por algún procedimiento;

2. asigna los restantes elementos al elemento más cercano de los previamente seleccionados;

3. sustituye los elementos seleccionados en (1) por los centroides de los grupos que se han formado;

4. asigna el conjunto de elementos al centroide más cercano del punto (3);

5. repite iterativamente los dos últimos pasos hasta que la asignación de elementos a los centroides no cambia. Los grupos entonces formados maximizan la distancia intergrupos y minimizan la distancia intragrupos.

Recuérdese que con el método de Forgy la etapa (3) no comienza hasta que no se hayan asignado todos los elementos a un clúster en la etapa (2), mientras que en “\(k\)-medias” los centroides se recomputan cada vez que un elemento es asignado a un grupo.

La partición que se obtiene es un óptimo local (pequeños cambios en la reasignación de elementos no lo mejoran), pero no se puede asegurar que sea el global, pues se trata de un método heurístico. Sí se puede asegurar que la partición es de calidad.

\(K\)-medias es eficiente y sencillo de implementar, pero tiene algunas desventajas: \((i)\) necesita conocer a priori el número de grupos; \((ii)\) la agrupación resultante puede depender de la asignación inicial (normalmente aleatoria) de los centroides, pudiendo converger a mínimos locales, por lo que se recomienda repetir la clusterización 25-50 veces y seleccionar la que tenga menor varianza intragrupos; \((iii)\) no es robusto a valores extremos; y \((iv)\) no trabaja con datos nominales.

En el ejemplo TIC se ha usado el algoritmo AS 136 de Hartigan & Wong (1979), una versión eficiente del de Hartigan (1975) que no busca óptimos locales (varianza intragrupos mínima en cada grupo), sino soluciones tales que ninguna reasignación de elementos reduzca la varianza (global) intragrupos (véase Fig. 31.1).

set.seed(123)
kmeans_tic <- eclust(tic, "kmeans", k = 3)

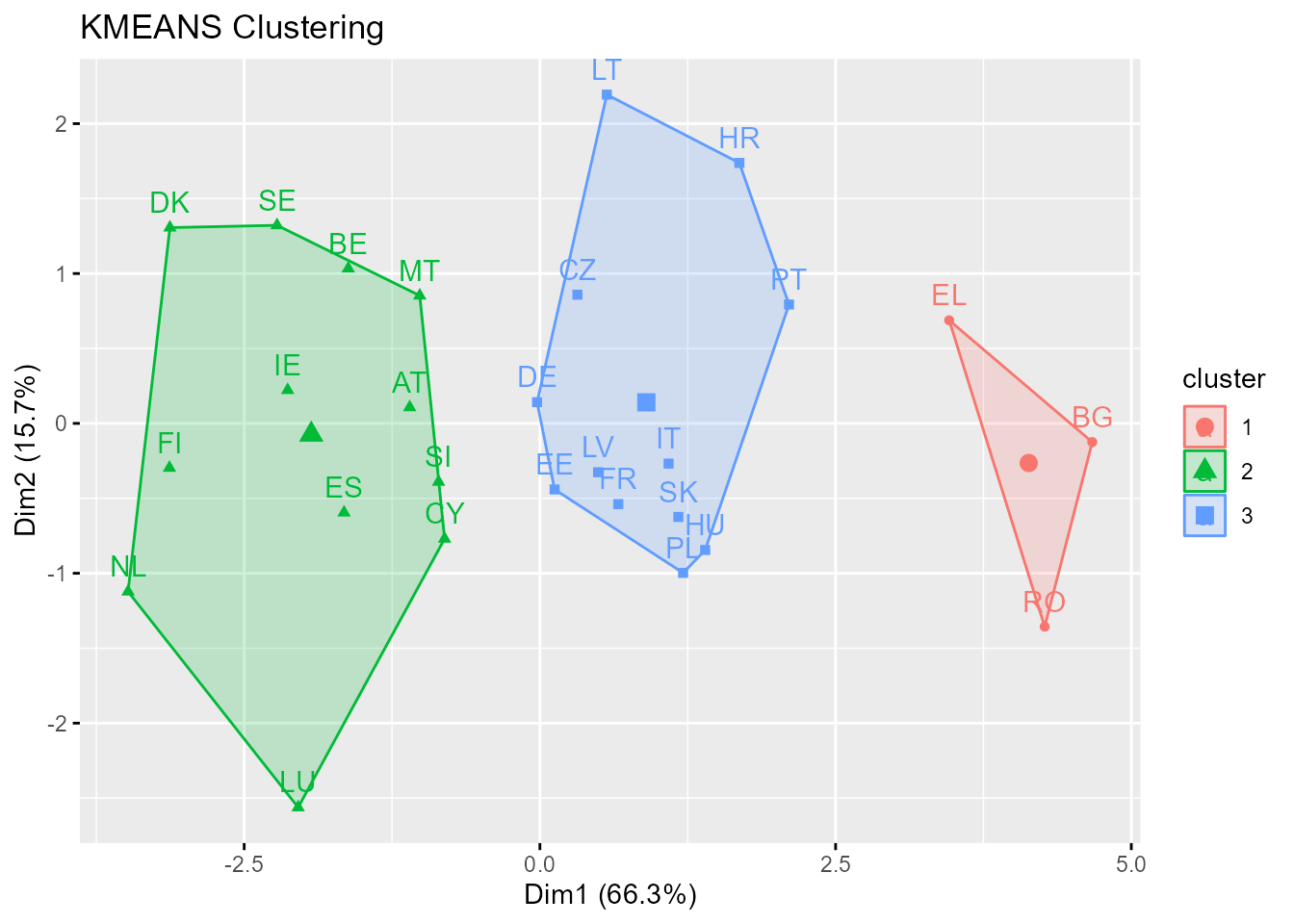
Figura 31.1: Clusterización no jerárquica con \(k\)-medias.

Algunas versiones del \(k\)-medias como el \(k\)-medias difuso, el \(k\)-medias recortadas, el \(k\)-medias armónicas, el \(k\)-medias sparse y el \(k\)-medias sparse robusto pueden verse en Carrasco-Oberto (2020).

31.2.2 Técnicas basadas en medoides

31.2.2.1 \(K\)-medoides (PAM)

Es un método de clusterización similar al \(k\)-medias que también requiere la especificación a priori del número de grupos. La diferencia es que en \(k\)-medoides cada grupo está representado por uno de sus elementos, denominados medoides (o centrotipos).²¹¹ En el \(k\)-medias están representados por sus centroides, que no tienen por qué coincidir con ninguno de los elementos a agrupar. Se trata, pues, de formar grupos particionando el conjunto de elementos alrededor de los medoides (PAM). Un ejemplo se encuentra en la Fig. 31.2.

El algoritmo \(k\)-medoides es más robusto al ruido y a valores grandes de los datos (de hecho es invariante a los outliers) que el \(k\)-medias, ya que minimiza la suma de diferencias por parejas (utiliza la distancia Manhattan) en lugar de la suma de los cuadrados de las distancias euclídeas.²¹² Además, sus agrupaciones no dependen del orden en que han sido introducidos los elementos, cosa que puede ocurrir con otras técnicas no jerárquicas, y, como se avanzó anteriormente, propone como centro del clúster un elemento del mismo.

PAM funciona muy bien con conjuntos de datos pequeños (por ejemplo, 100 elementos en 5 grupos) y permite un análisis detallado de la partición realizada, puesto que proporciona las características del agrupamiento y un gráfico de silueta, así como un índice de validez propio para determinar el número óptimo de clústeres. El algoritmo PAM puede verse al completo en Kaufman & Rousseeuw (1990); para un muy buen resumen véase Amat Rodrigo (2017).

set.seed(123)
pam_tic <- eclust(tic, "pam", k = 3)

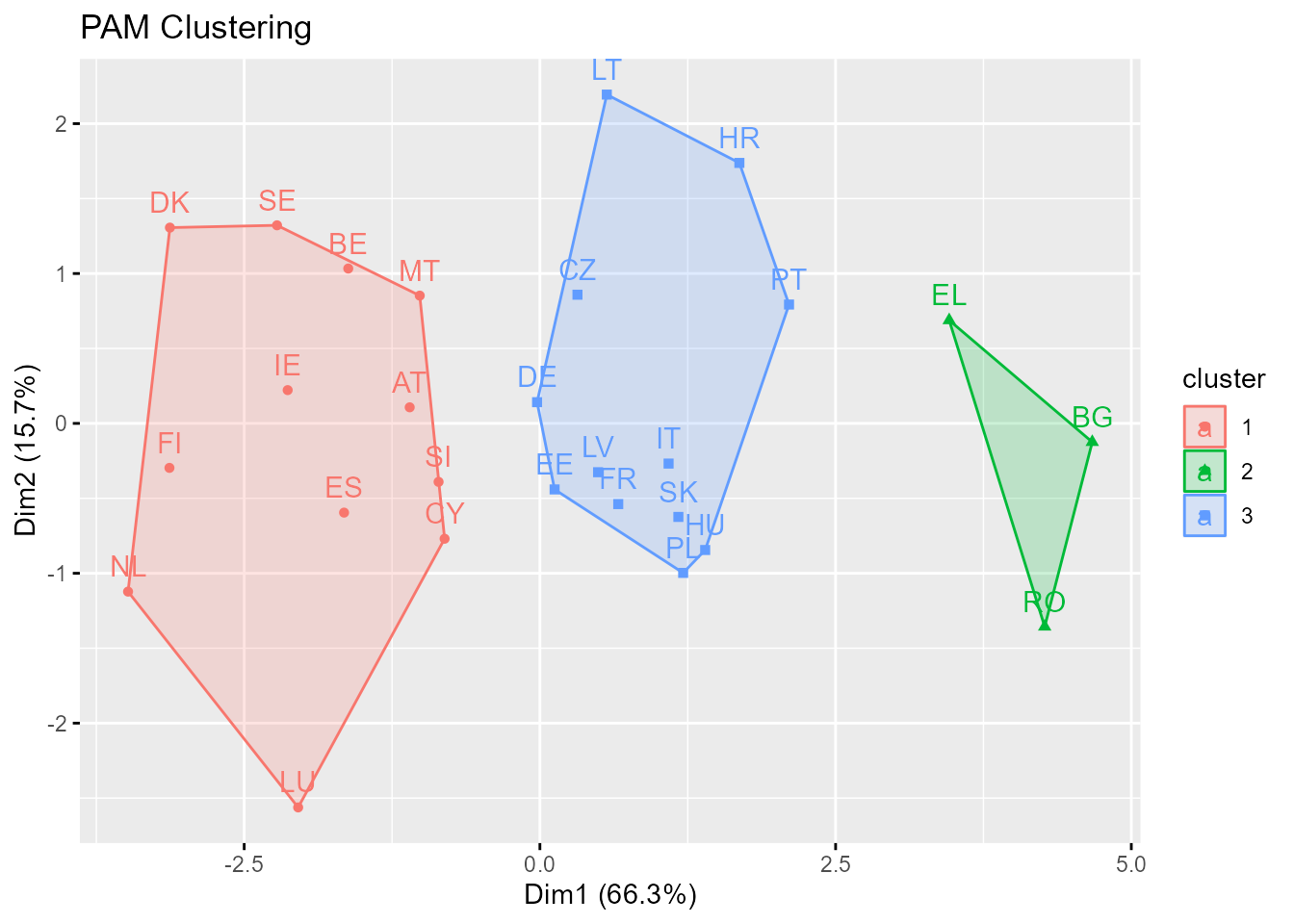
Figura 31.2: Clusterización no jerárquica con PAM.

31.2.2.2 CLARA

La ineficiencia de PAM para bases de datos grandes, junto con su complejidad computacional, llevó al desarrollo de CLARA (clustering large applications).²¹³

La diferencia entre PAM y CLARA es que el segundo se basa en muestreos. Solo una pequeña porción de los datos totales es seleccionada como representativa de los datos y los medoides son escogidos (en la muestra) usando PAM. CLARA, pues, combina la idea de \(k\)-medoides con el remuestreo para que pueda aplicarse a grandes volúmenes de datos. De acuerdo con Amat Rodrigo (2017), CLARA selecciona una muestra aleatoria y le aplica el algoritmo de PAM para encontrar los clústeres óptimos dada esa muestra.²¹⁴ Alrededor de esos medoides se agrupan los elementos de todo el conjunto de datos. La calidad de los medoides resultantes se cuantifica con la suma total de distancias intragrupos. CLARA repite este proceso un número predeterminado de veces con el objetivo de reducir el sesgo de muestreo. Por último, se seleccionan como clústeres finales los obtenidos con los medoides que minimizaron la suma total de distancias intragrupo. Se presenta un ejemplo en la Fig. 31.3.

set.seed(123)
clara_tic <- eclust(tic, "clara", k = 3)

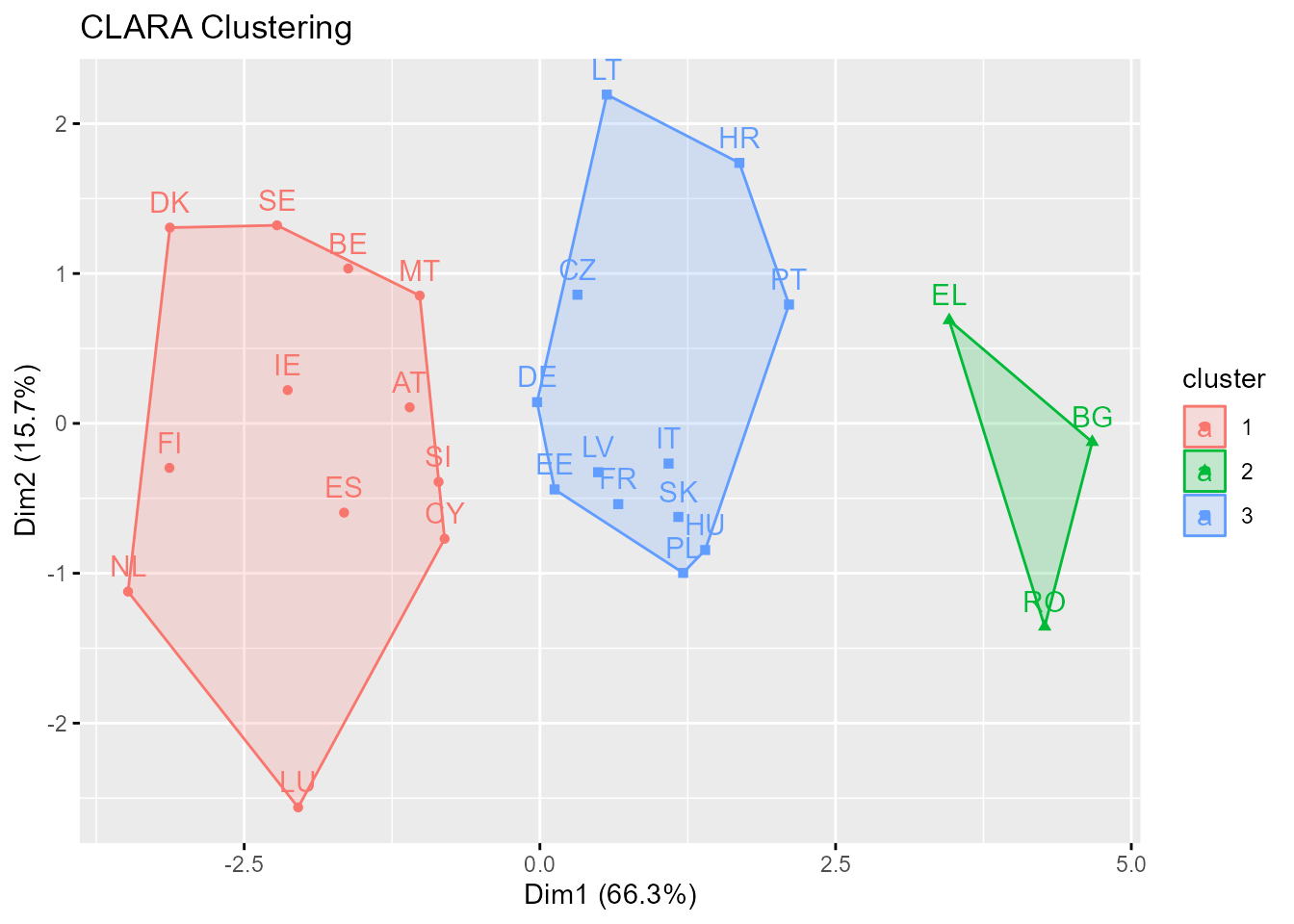
Figura 31.3: Clusterización no jerárquica con CLARA.

31.2.2.3 CLARANS

CLARANS (del inglés clustering large applications based upon randomized search) es una mezcla de PAM y CLARA. Como CLARA puede dar lugar a una mala clusterización si uno de los medoides de la muestra está lejos de los mejores medoides, CLARANS trata de superar esta limitación. El algoritmo puede verse en Ng & Han (2002).

31.2.3 Técnicas basadas en medianas: \(k\)-medianas

Igual que el \(k\)-medoides, es una variante del \(k\)-medias que utiliza como centros las medianas para que no le afecten ni el ruido ni los valores atípicos. La diferencia con el \(k\)-medoides es que la mediana de un grupo no tiene por qué ser una de las observaciones. \(K\)-medianas utiliza la distancia Manhattan.

Volviendo al ejemplo TIC, como se ha podido comprobar, la clusterización de los países de la UE-27 en función del uso del las TIC es prácticamente la misma con técnicas jerárquicas aglomerativas como el vecino más lejano, el método de Ward, el del centroide, o algoritmos divisivos como DIANA, que con las técnicas no jerárquicas con preselección de 3 grupos (\(k\)-medias, PAM y CLARA).

31.3 Métodos basados en la densidad de elementos

Utilizan indicadores de frecuencia, construyendo grupos mediante la detección de aquellas zonas del espacio de las variables (que caracterizan a los elementos) densamente pobladas (clústeres naturales) y de aquellas otras con un escasa densidad de elementos. Los elementos que no forman parte de un conglomerado se consideran ruido. Emulan, pues, el funcionamiento del cerebro humano.

La identificación de los grupos (y los parámetros que los caracterizan, cuando se manejan modelos probabilísticos) se lleva a cabo haciéndolos crecer hasta que la densidad del grupo más próximo sobrepase un cierto umbral. Por tanto, imponen reglas para evitar el problema de obtener un solo grupo cuando existen puntos intermedios. Se suele suponer que la densidad de elementos en los grupos es Gaussiana si las variables son cuantitativas, y multinomial si son cualitativas.

Se suelen clasificar en:

• Los que tienen un enfoque tipológico: los grupos se construyen buscando las zonas con mayor concentración de elementos. Pertenecen a este tipo el análisis modal de Wishart, que supone clústeres esféricos y dada la complejidad de su algoritmo no tuvo mucho éxito, el método TaxMap, que introduce un valor de corte en caso de que los grupos no estén claramente aislados (ello lleva a que los resultados tengan un cierto grado de subjetividad), y el método de Fortin, también con muy escasa difusión en la literatura.

• Los que tienen un enfoque probabilístico: las variables que caracterizan los elementos siguen una distribución de probabilidad cuyos parámetros cambian de un grupo a otro. Se trata, pues, de agrupar los elementos que pertenecen a la misma distribución. Un ejemplo es el método de las combinaciones de Wolf.

No obstante, estos algoritmos y otros como, por ejemplo, los de Gitman y Levine, y Catel y Coulter, aunque muy citados en la literatura en español, tuvieron poco éxito.

Mayor éxito han tenido otros algoritmos como expectation-maximization (EM), model based clustering (MCLUST), density-based spatial clustering of applications with noise (DBSCAN), ordering points to identify the clustering structure (OPTICS), que es una generalización de DBSCAN, wavelet-based cluster (WAVECLUSTER) y density-based clustering (DENCLUE), entre otros.

DBSCAN²¹⁵ es, quizás, el más popular. Incluso ha recibido premios por sus numerosísimas aplicaciones a lo largo del tiempo. Soluciona los problemas de los métodos de reasignación, que son buenos para clústeres con forma esférica o convexa que no tengan demasiados outliers o ruido, pero que fallan cuando los clústeres tienen formas arbitrarias. De acuerdo con Amat Rodrigo (2017), DBSCAN evita este problema siguiendo la idea de que \((i)\) para que una observación forme parte de un clúster, tiene que haber un mínimo de observaciones vecinas dentro de un radio de proximidad y \((ii)\) que los clústeres están separados por regiones vacías o con pocas observaciones. Consecuentemente, DBSCAN necesita dos parámetros: el radio (\(\epsilon\)) que define la región vecina a una observación (\(\epsilon\)-neighborhood); y el número mínimo de puntos (minPts) u observaciones en ella.²¹⁶

Los elementos objeto de agrupación se pueden clasificar, en función de su \(\epsilon\)-neighborhood y minPts, como:

1. elementos centrales, si el número de elementos en su \(\epsilon\)-neighborhood es igual o mayor que minPts;

2. elementos frontera, si no son elementos centrales pero pertenecen al \(\epsilon\)-neighborhood de otro elemento que sí es central; y

3. elementos atípicos o de ruido, si no verifican ni (1) ni (2).

A partir de la clasificación anterior, y para \(\epsilon\)-neighborhood y minPts dados, se origina otra:

1. un elemento \(Q\) es denso-alcanzable directamente desde el elemento \(P\) si \(Q\) está en el \(\epsilon\)-neighborhood de \(P\) y \(P\) es un elemento central;

2. \(Q\) es denso-alcanzable desde \(P\) si existe una cadena de objetos \(\{Q_{1}=P, Q_2, Q_3,..., Q_{n}\}\) tal que \(Q_{i+1}\) es denso-alcanzable directamente desde \(Q_{i}\), \(\forall 1 \leq i \leq n\);

3. \(Q\) está denso-conectado con \(P\) si hay un elemento \(R\) desde el cual \(P\) y \(Q\) son denso-alcanzables.

Los pasos del algoritmo DBSCAN son los siguientes (Amat Rodrigo, 2017):

• Para cada elemento u observación \(x_i\) calcúlese su distancia con el resto de observaciones. Márquese como central si lo es y como visitado si no lo es.

• Para cada observación marcada como elemento central, si aún no ha sido asignada a ningún grupo, créese un grupo nuevo y asígnesele a él. Búsquense, recursivamente, todas las observaciones denso-conectadas con ella y asígnense al mismo grupo.

• Itérese el mismo proceso para todas todas las observaciones no visitadas.

• Aquellas observaciones que tras haber sido visitadas no pertenecen a ningún clúster se marcan como outliers.

Como resultado del algoritmo DBSCAN se generan clústeres que verifican: \((i)\) todos los elementos que forman parte de un mismo clúster están denso-conectados entre ellos; y \((ii)\) si un elemento \(P\) es denso-alcanzable desde cualquier otro de un clúster, entonces \(P\) también pertenece al clúster.

El éxito de DBSCAN se debe a sus importantes ventajas. De nuevo siguiendo a Amat Rodrigo (2017), no requiere la especificación previa del número de clústeres; no require esfericidad (ni ninguna forma determinada) en los grupos; y puede identificar valores atípicos, por lo que la clusterización resultante no vendrá influenciada por ellos. También tiene algunas desventajas, como que no es un método totalmente determinista puesto que \((i)\) los puntos frontera que son denso-alcanzables desde más de un clúster pueden asignarse a uno u otro dependiendo del orden en el que se procesen los datos; y \((ii)\) no genera buenos resultados cuando la densidad de los grupos es muy distinta, ya que no es posible encontrar un \(\epsilon\)-neighborhood y un minPts válidos para todos a la vez.

Dado el escaso número de datos de la base de datos TIC2021 del paquete CDR no se puede utilizar DBSCAN. Sin embargo, para ilustrar su utilización, la Fig. 31.4 muestra la agrupación en 5 clústeres de la base de datos multishapes de la librería factoextra mediante DBSCAN (función dbscan()) y \(k\)-medias. Se trata de una base de datos que contiene observaciones pertenecientes a 5 grupos distintos y con cierto ruido (outliers); en consecuencia, los grupos no deberían ser esféricos y DBSCAN sería un algoritmo de agrupación adecuado.

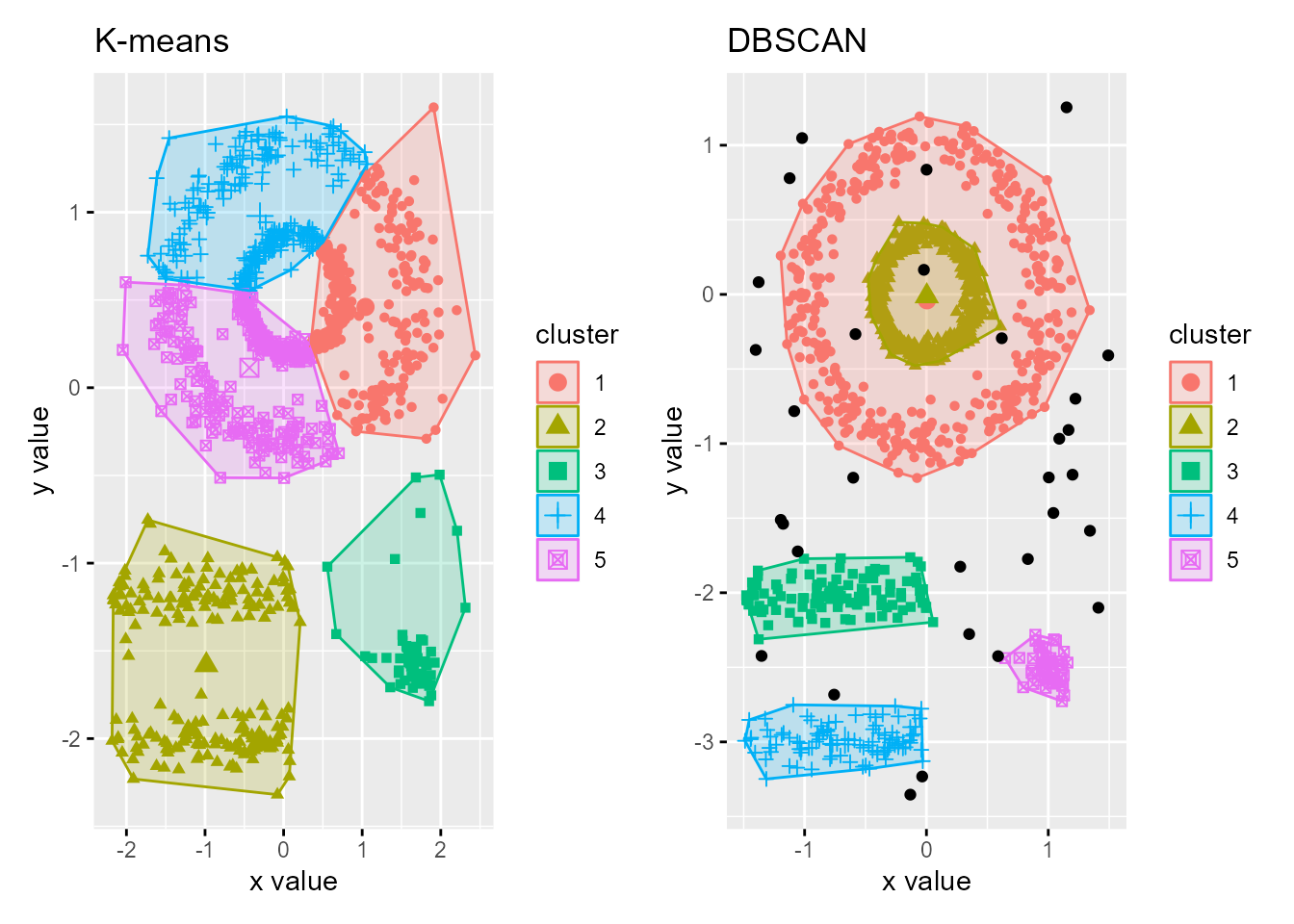
Figura 31.4: Comparación entre los algoritmos \(k\)-means y DBSCAN para el conjunto de datos simulado \(multishapes\).

31.4 Otros métodos

Por último, en el cajón de sastre de otras técnicas de clusterización no jerárquicas, merece la pena siquiera mencionar los métodos directos, los de reducción de la dimensionalidad, los de clustering difuso y la clusterización basada en modelos.

Los métodos directos agrupan simultáneamente los elementos y las variables. El más conocido es el clúster por bloques (\(block\)-; \(bi\)-; \(co\)-; o two-mode clustering). El paquete biclust proporciona varios algoritmos para encontrar clústeres en dos dimensiones. Además, es muy recomendable para el preprocesamiento de los datos y para la visualización y validación de los resultados.

Las técnicas de reducción de la dimensionalidad buscan factores en el espacio de los elementos (modelo \(Q\)-factorial) o de las variables (modelo \(R\)-factorial) haciendo corresponder un clúster a cada factor. Centrándonos en el modelo \(Q\)-factorial, el método parte de la matriz de correlaciones entre los elementos y rota ortogonalmente los factores encontrados. Dado que los elementos pueden pertenecer a varios clústeres y, por tanto, los clústeres pueden solaparse, su interpretación se hace muy difícil.

Las técnicas de clustering difuso precisamente permiten la pertenencia de un elemento a varios clústeres, estableciendo un grado de pertenencia a cada uno de ellos. El algoritmo de clustering difuso más popular es fuzzy c-medias, muy similar al k-medias, pero que calcula los centroides como una media ponderada (la ponderación es la probabilidad de pertenencia) y, lógicamente, proporciona la probabilidad de pertenencia a cada grupo.

La clusterización basada en modelos tiene un enfoque estadístico y consiste en la utilización de una mixtura finita de modelos estocásticos para la construcción de los grupos.

Un vector aleatorio \(\bf X\) procede de una mixtura finita de distribuciones paramétricas si \(\forall \bf x \subset \bf X\) su función de densidad conjunta se puede escribir como \(f{(\bf {x} | \bf {\psi})}=\sum_{g=1}^{G} {\pi_g} f_g {(\bf {x}|\bf {\theta_g})},\) donde \(\pi_g\) son las proporciones asignadas a cada grupo en la mixtura, tal que \(\sum_{g=1}^{G} \pi_g =1\); \(f_g(\bf x|\theta_g)\) es la función de densidad correspondiente al \(g\)-ésimo grupo y \(\bf \psi=(\pi_1, \pi_2,..., \pi_G, \bf \theta_1,\bf \theta_2,...\bf \theta_G\)). Las funciones de densidad \(f_g {(\bf {x}|\bf {\theta_g})}\) suelen ser idénticas para todos los grupos.

En términos menos formales, el clustering basado en modelos considera que los datos observados (multivariantes) han sido generados a partir de una combinación finita de modelos componentes (distribuciones de probabilidad, normalmente paramétricas). A modo de ejemplo, en un modelo resultante de una mixtura de normales multivariantes (el caso habitual), cada componente (clúster) es una normal multivariante y el componente responsable de la generación de una observación específica determina el grupo al que pertenece dicha observación. Para la estimación de la media y matriz de covarianzas se suele recurrir al algoritmo expectation-maximization, una extensión del \(k\)-medias.²¹⁷ El paquete mclust utiliza la estimación máximo verosímil para estimar dichos modelos con distintos número de clústeres, utilizando el Bayesian information criterion (BIC) para la selección del mejor.

Sus limitaciones fundamentales son (\(i\)) considerar que las características de los elementos son independientes y (\(ii\)) que no es recomendable para grandes bases de datos o distribuciones de probabilidad que impliquen un elevado coste computacional.

Una revisión de la evolución de la clusterización basada en modelos desde sus orígenes en 1965 puede verse en McNicholas (2016). Para una idea intuitiva, véase Amat Rodrigo (2017).

31.5 Nota final

La elección de qué técnica de clusterización utilizar, jerárquica o no, es una decisión del investigador, y dependerá de cómo quiera realizar la agrupación, la métrica de las variables y la distancia o medida de similaridad elegida. No obstante, ambos tipos de técnicas tienen sus ventajas y desventajas, y deberán ser tenidas en cuenta a la hora de decidir. Las jerárquicas adolecen de cierta inestabilidad, lo que plantea dudas sobre la fiabilidad de sus resultados. Además, a veces es difícil decidir cuántos grupos deben seleccionarse. Suelen recomendarse en caso de conjuntos de datos pequeños. En caso de grandes conjuntos de datos, la literatura suele recomendar las no jerárquicas; además, tienen una gran fiabilidad, ya que al permitir la reasignación de los elementos, una incorrecta asignación puede ser corregida posteriomente.

Resumen

En este capítulo se pasa revista a las principales técnicas y algoritmos de agrupación no jerárquicas.

• Se abordan los principales métodos de reasignación, y en particular los basados en centroides (método de Forgy y \(k\)-medias), medoides (\(k\)-medoides, PAM, CLARA, CLARANS) y medianas (\(k\)-medianas).

• Se exponen las técnicas basadas en la densidad de puntos desde las perspectivas tipológica (análisis modal, métodos TaxMap, de Fortin, de Gitman y Levine, y de Catel y Coulter) y probabilística (método de Wolf), así como se estudia el DBSCAN.

• Se muestran otras técnicas de agrupación no jerárquicas como los métodos directos (\(block\)-; \(bi\)-; \(co\)-; two-mode clustering), los de reducción de la dimensionalidad (modelos \(Q\)- y \(R\)-factorial), el clustering difuso y los métodos basados en mixturas de modelos.