Capítulo 10 Herramientas para el análisis en ciencia de datos

José-María Montero\(^{a}\) y Jorge Velasco López\(^{b}\)

\(^{a}\)Universidad de Castilla-La Mancha
\(^{b}\)Instituto Nacional de Estadística de España

10.1 Introducción

En este capítulo se describen una serie de herramientas necesarias para desarrollar proyectos de ciencia de datos. Son herramientas que se utilizan pre o postmodelado de los datos y que aumentan significativamente el rendimiento de los modelos. Tal caja de herramientas incluye el particionado del conjunto de datos, el manejo de datos no equilibrados,⁷⁶ los métodos de remuestreo, el equilibrio entre sesgo y varianza, el ajuste de hiperparámetros y la evaluación de modelos, entre otras.

Para ilustrar el manejo de las herramientas anteriormente mencionadas, se utiliza el conjunto de datos Madrid_Sale (disponible en el paquete de R idealista18), con datos inmobiliarios del año 2018 para el municipio de Madrid. En cuanto al software R, se utiliza caret (Kuhn, 2008), para diversas tareas de preparación de datos, y rsample, para muestreo.

10.2 Partición del conjunto de datos

El objetivo principal del proceso de ciencia de datos es encontrar el modelo o algoritmo que mejor resuelva la pregunta de investigación o, lo que es lo mismo, que proporcione mejores resultados. Por ejemplo, en el caso de los modelos de predicción (y en general de aquellos en los que el aprendizaje es supervisado), muy populares en la ciencia de datos, hay que encontrar el que prediga con mayor exactitud los valores futuros de la variable objetivo a partir de los predictores seleccionados en el conjunto de datos disponible. En otras palabras, un algoritmo que no solo ajuste bien los datos pasados sino, lo que es más importante, que proporcione predicciones (futuras) acertadas (y precisas). Para ello, inicialmente, se dividen los datos en dos subconjuntos:

• de entrenamiento (training): se utiliza para desarrollar conjuntos de funciones, entrenar algoritmos, ajustar hiperparámetros, comparar modelos y realizar todas las demás actividades necesarias para seleccionar un modelo final.
• de prueba (test): se utiliza para validar la precisión del modelo seleccionado en la fase de entrenamiento.

A la hora de dividir el conjunto de datos en los dos subconjuntos anteriores, hay que tomar dos decisiones:

• ¿Qué porcentaje de los datos (casos, observaciones) se incluye en cada subconjunto?
• ¿Cómo se seleccionan los casos u observaciones que van a cada subconjunto?

Por lo que se refiere a la primera decisión, cuanto más grande sea el subconjunto de entrenamiento, mejor será el predictor (o clasificador), aunque las mejoras serán cada vez más pequeñas. Por el contrario, cuanto más grande sea el subconjunto de prueba o test, más precisa será la estimación del error de predicción. En otros términos, lo ideal sería tener un conjunto de datos muy grande y que ambos subconjuntos fueran grandes. De esta manera, los errores de predicción serían pequeños y tendrían poca variabilidad. Sin embargo, con frecuencia, este no es el caso en la práctica, y el dilema es elegir un buen predictor (o clasificador) o una buena estimación del error de predicción. En la práctica, lo más frecuente es incluir el 70% de los datos en el subconjunto de entrenamiento y el 30% restante en el de test, aunque los repartos 80% - 20% y 60% - 40% también son muy populares.

En cuanto a la segunda decisión, la respuesta es: mediante métodos de muestreo, siendo los más utilizados el muestreo aleatorio simple y el muestreo aleatorio estratificado (véase Cap. 13).

10.2.1 Muestreo aleatorio simple

La forma más sencilla de asignar los datos a los subconjuntos de entrenamiento y prueba es tomar una muestra aleatoria simple (m.a.s.) (véase Sec. 13.2) del conjunto de casos u observaciones del tamaño deseado, y asignarlos al subconjunto de entrenamiento, asignándose los restantes al conjunto de test.

Un problema que puede surgir con las m.a.s. es que, cuando el conjunto de datos es pequeño y los valores de uno (o más) de los predictores están muy desequilibrados (por ejemplo, el predictor es binario y el 95% de sus valores pertenecen a una clase o categoría y el 5% restante a la otra), hay una probabilidad nada desdeñable de que en alguno de los dos subconjuntos (sobre todo en el de test) dicho predictor no esté representado. Si esta circunstancia ocurriese en el conjunto de entrenamiento, algunos algoritmos darían error al aplicarlos al conjunto de test (donde habría datos de un predictor más). Si, por el contrario, ocurriese en el conjunto de test, los problemas surgirían por haber un predictor menos que en el conjunto de entrenamiento. Los problemas se agravarían si la desproporción anterior tuviese lugar en la variable objetivo.

A continuación, se realiza una división⁷⁷ 70% - 30% en el conjunto de datos Madrid_Sale_num, generado en el Cap. 9. Para que se pueda reproducir, se establece al principio una semilla determinada.

library ("caret")

set.seed(123) # para permitir reproducirlo
index <- createDataPartition(Madrid_Sale_num$PRICE, p = 0.7, list = FALSE)
train <- Madrid_Sale_num[index, ]
test <- Madrid_Sale_num[-index, ]
dim(Madrid_Sale_num) # 94815
dim(train) # 66373
dim(test) # 28442

Como puede comprobarse, de los 94.815 datos que contiene Madrid_Sale_num, 66.373 (el 70%), pasan a formar parte del conjunto de entrenamiento y, el resto, 28.442, constituyen el conjunto de test.

10.2.2 Muestreo estratificado

Si se desea controlar el muestreo para que los subconjuntos de entrenamiento y prueba tengan distribuciones similares en las clases de la variable objetivo,⁷⁸ se puede usar muestreo estratificado (véase Sec. 14.3).⁷⁹ Sin embargo, este tipo de muestreo, estratificando por la variable objetivo, no garantiza que ocurra lo mismo con los predictores. Es decir, presenta la misma limitación que el muestreo aleatorio simple en caso de que algún (o algunos) predictores estén muy desequilibrados y se quiera garantizar que en ambos subconjuntos las clases de la variable respuesta estén representadas de forma similar. Una posible solución es la eliminación de dichos predictores (que tendrán varianza próxima a cero), si bien ello implica pérdida de información.

A continuación, se estratifica el conjunto de datos Madrid_Sale_num_sample_bin del Cap. 9 por la variable objetivo (price_bin, el precio de venta con binning), que tiene cuatro categorías.

library("rsample")

set.seed(123) # para permitir reproducirlo
table(Madrid_Sale_num_sample_bin$price_bin) |> prop.table()
#         0.4776    0.3062    0.1024    0.1116
split_estrat <- initial_split(Madrid_Sale_num_sample_bin, prop = 0.7, strata = "price_bin")
train_estrat <- training(split_estrat)
test_estrat <- testing(split_estrat)

Como puede comprobarse debajo, al generar muestras aleatorias estratificadas por la variable objetivo, la distribución de estas en los subconjuntos de entrenamiento y de prueba es aproximadamente igual:

table(train_estrat$price_bin) |> prop.table()
#   0.4777015 0.2913093 0.1132075 0.1177816
table(test_estrat$price_bin) |> prop.table()
#   0.4799886 0.3061750 0.1023442 0.1114923

10.3 Técnicas para manejar datos no equilibrados

A menudo, los datos utilizados en determinadas áreas tienen menos del 1% de eventos raros, pero precisamente su rareza es lo que los hace “interesantes”: por ejemplo, estafas en operaciones bancarias o usuarios que hacen clic en anuncios. En otros términos, una de las clases de la variable objetivo es dominante, pero la clase minoritaria es la que presenta interés. Sin embargo, la mayoría de los algoritmos no funcionan bien con variables cuyas clases están desequilibradas (kuhn2013applied?). Hay varias técnicas para manejar este problema:

• Downsampling:⁸⁰ equilibra el conjunto de datos reduciendo el tamaño de las clases abundantes para que coincida con el de la clase menos prevalente. Este método es de utilidad cuando el tamaño del conjunto de datos es suficientemente grande para ser aplicado.
• Upsampling:⁸¹ equilibra el conjunto de datos aumentando el tamaño de las clases más raras. En lugar de deshacerse de datos de las clases abundantes, se generan nuevos datos para las clases raras mediante repetición o bootstrapping. Este procedimiento es de utilidad cuando no hay suficientes datos en la clase (o clases) rara.
• Creación de datos sintéticos: esta técnica consiste en equilibrar el conjunto de entrenamiento generando nuevos registros sintéticos, esto es, inventados, de la clase minoritaria. Existen diversos algoritmos que realizan esta tarea, siendo uno de los más conocidos la técnica de SMOTE (Synthetic Minority Oversampling Technique) (Chawla et al., 2002).
• Otras técnicas: como que el algoritmo implemente mecanismos para dar mayor peso a los casos de la clase minoritaria, etc.

A modo de ejemplo, a continuación se utiliza downsampling en el conjunto de datos Madrid_Sale_num_sample_bin, para mejorar la precisión del modelo, mediante el algoritmo gradient-boosting:

# Se especifica que el modelo se entrene con downsampling
ctrl <- trainControl(
  method = "repeatedcv", repeats = 5,
  classProbs = TRUE,
  sampling = "down"
)
Madrid_Sale_num_sample_bin_downsample <- train(price_bin ~ .,
  data = Madrid_Sale_num_sample_bin,
  method = "gbm",
  preProcess = c("range"),
  verbose = FALSE,
  trControl = ctrl
)

No existe una ventaja absoluta de un método sobre otro. La aplicación de estos métodos depende del caso de uso al que se aplique y del conjunto de datos. La función de caret para implementar estas técnicas está en ?caret::trainControl()).

Una alternativa a los métodos anteriores es la implementación de algoritmos que proporcionen un buen rendimiento con variables cuyas clases están desequilibradas, de tal manera que se refuerce el aprendizaje en la clase minoritaria. La idea detrás de esta segunda opción es incluir una penalización o un sesgo que pondere las clases de tal manera que se le dé más importancia a la predicción, clasificación, etc. correcta en la clase minoritaria (para más detalles, véase García Abad, 2021).

10.4 El enfoque de validación

Anteriormente, se indicaba que los datos deben dividirse en dos subconjuntos, uno de entrenamiento y otro de prueba, y que no debía usarse el subconjunto de prueba para evaluar la exactitud del modelo durante la fase de entrenamiento. Si la exactitud de las predicciones (por ejemplo, porcentaje de casos bien clasificados en un problema de clasificación) en el conjunto de test es (además de elevada) similar a la que se obtiene en el conjunto de entrenamiento, entonces el modelo entrenado generalizará bien para otros conjuntos de datos y puede darse por bueno. En otro caso, el modelo no ha entrenado bien. Por ejemplo, si la exactitud de las predicciones en el conjunto de entrenamiento es del 80% y en el de test es del 25% o del 97%, entonces el modelo no puede darse por válido. En el caso del 97%, la diferencia de porcentajes está indicando un aprendizaje “excesivo” del conjunto de datos de entrenamiento, de tal manera que el modelo en cuestión puede proporcionar muy buenas predicciones para el conjunto de datos utilizado, pero no para nuevos datos, o conjuntos de datos (esta circunstancia se conoce como sobreajuste u overfitting).⁸²

En el caso en el que la exactitud de las predicciones sea muy distinta en los subconjuntos de entrenamiento y test, hay varias opciones (no excluyentes) para salvar dicha circunstancia: mejorar el modelo, ajustar sus hiperparámetros, incluir más casos en el conjunto de datos, modificar el preprocesado de los datos, ver si hay desequilibrio entre las clases, analizar si las variables predictoras son o no las adecuadas, revisar el proceso de limpieza de datos… y, posteriormente, entrenar de nuevo el modelo y determinar si es o no válido. Otra opción más drástica es, simplemente, cambiar de modelo.

Una mejor opción sería utilizar desde el principio un enfoque de validación, que implica dividir el subconjunto de entrenamiento en dos partes: un subconjunto de entrenamiento propiamente dicho y un conjunto de validación. Así, se puede entrenar el modelo en el nuevo subconjunto de entrenamiento y estimar su exactitud en el conjunto de validación. Es importante tener claro que el subconjunto de validación no es un subconjunto que se deje aparte, como el de test, durante la fase de entrenamiento, sino que se utiliza en dicha fase.

En resumen, con el enfoque de validación, para dar por válido un modelo, se procede como sigue:

• Dividir el conjunto de datos en subconjunto de entrenamiento y subconjunto de test.
• Dividir el subconjunto de entrenamiento en un subconjunto de entrenamiento propiamente dicho y un subconjunto de validación.
• Entrenar el modelo con los datos del subconjunto de entrenamiento propiamente dicho.
• Comprobar que la exactitud de las predicciones en dicho subconjunto de entrenamiento y en el de validación es similar (y aceptable para la exigencia que se requiere).
• Realizar predicciones con el conjunto de test y comprobar que se obtiene un porcentaje de buenas predicciones aceptable para los requisitos exigidos.
• Agregar el conjunto de test al de entrenamiento (global) y entrenar de nuevo el modelo (que será el definitivo); de esta manera se aprovecha el 100% de los datos. Este último entrenamiento debería mejorar el modelo final, aunque la única manera de comprobarlo es mediante su comportamiento en el entorno real.

La limitación del enfoque de validación con un solo subconjunto de reserva (de validación) es que dicha validación puede ser muy variable y poco confiable, a menos que se esté trabajando con conjuntos de datos muy grandes (Molinaro et al., 2005). Y aquí es donde entran en juego los procedimientos de validación que utilizan remuestreo. El procedimiento de validación con remuestreo más utilizado es la validación cruzada (VC) k-grupos (k-fold cross validation). También es muy popular el que utiliza remustreo por bootstrapping, que se abordará tras la VC de k-grupos.

Para llevar a cabo una VC k-grupos, se divide aleatoriamente el subconjunto de datos de entrenamiento en \(k\) grupos (folds) de aproximadamente el mismo tamaño. El modelo se ajusta en los \(k-1\) primeros grupos y el último se usa como conjunto de validación, para “validar” la bondad del modelo. A continuación, se separa el penúltimo grupo y se ajusta el modelo con los restantes, usándose el penúltimo grupo como subconjunto de validación para validar la bondad del modelo. Después se separa el antepenúltimo grupo, y así sucesivamente, hasta separar el primero. Como resultado, se obtienen \(k\) conjuntos de errores, cuyo promedio (véase Sec. 10.7) podría servir como estimación de la exactitud y precisión (o error⁸³) esperada en un conjunto de datos nuevo.

El procedimiento descrito puede repetirse varias veces (VC con repetición), mediante nuevas particiones aleatorias del conjunto de entrenamiento y procediendo igual que en la iteración anterior.

En la práctica, normalmente se usa \(k=5\) o \(k=10\) (las Fig. 10.1 y 10.2 ilustran el caso de VC 5-grupos). No existe una regla formal en cuanto al tamaño de \(k\), pero a medida que \(k\) aumenta, la diferencia entre el rendimiento estimado y el real, así como entre la precisión estimada y la real que se obtendrá en el conjunto de test disminuirá. En el lado negativo de la balanza, un valor de \(k\) demasiado grande puede aumentar notablemente la carga computacional y, además, no generar mejoras significativas. A este respecto, en Molinaro et al. (2005) se concluye que VC con \(k=10\) funciona de manera similar a VC con \(k=n\), la VC más extrema, también conocida como VC “dejando uno fuera” (leave one out cross validation, LOOCV).

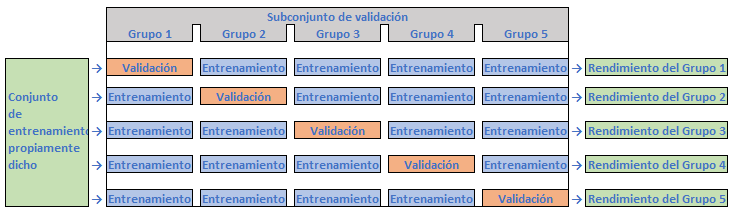
Figura 10.1: VC 5-grupos (i).

Y si la exactitud de las predicciones en el subconjunto de entrenamiento propiamente dicho y en el de validación es similar (y aceptable para la exigencia que se requiere):

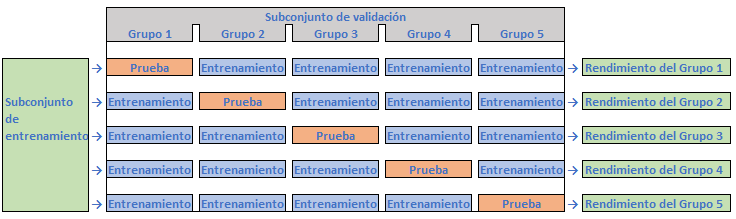
Figura 10.2: VC 5-grupos (ii).

Aunque \(k\geq 10\) contribuye a minimizar la variabilidad del error de predicción (es decir, tiende a aumentar la precisión de las predicciones), en general la VC k-grupos suele proporcionar mayores variabilidades que el bootstrapping (que se analiza a continuación); no ocurre lo mismo con el sesgo (Boehmke & Greenwell, 2020). Kim (2009) demostró que repetir el VC k-grupos puede ayudar a reducir la estimación del error de generalización.

Una implementación del VC k-grupos, con tres repeticiones, utilizando el conjunto de datos Madrid_Sale_num_sample_bin, previa mejora de la precisión del modelo mediante downsampling, se llevó a cabo en la Sec. 10.3 con la siguiente orden:

control <- trainControl(method = "repeatedcv", number = 10, repeats = 3)

Bootstrapping es un procedimiento de muestreo aleatorio con reemplazamiento (Efron & Tibshirani, 1986). Esto significa que, después de seleccionar un dato para incluirlo en el subconjunto que sea, sigue disponible para una selección posterior. Una muestra bootstrap tiene el mismo tamaño que el conjunto de datos original a partir del cual se obtiene. Las observaciones originales seleccionadas (una o varias veces) en la muestra conforman el subconjunto de de entrenamiento, mientras que aquellas que no aparecen en ella (se las denomina out-of-bag) conforman el subconjunto de test.

La Fig. 10.3 (adaptada de Boehmke & Greenwell (2020)), muestra un esquema de muestreo bootstrap, donde cada muestra contiene 12 observaciones, al igual que en el conjunto de datos original. Como puede observarse, el muestreo bootstrap lleva aproximadamente a la misma distribución de valores (representados por colores) que el conjunto de datos original.

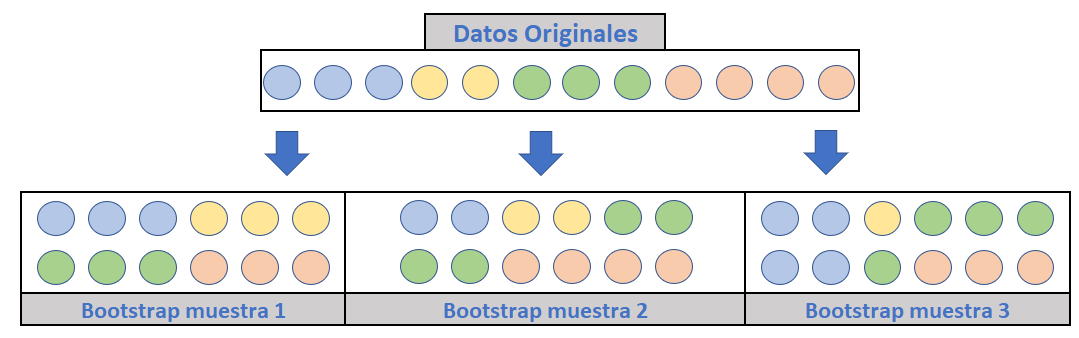
Figura 10.3: Remuestreo \(bootstrap\). Elaboración propia a partir de Boehmke and Greenwell (2019).

El hecho de que bootstrapping replique el conjunto de observaciones implica, como se dijo anteriormente, que la variablidad del error es menor que en VC k-grupos. Sin embargo, dicha replicación puede aumentar el sesgo de la estimación de dicho error. Esto puede ser un problema con conjuntos de datos muy pequeños, pero no para la mayoría de los conjuntos de datos, que suelen ser de tamaño medio o grande (por ejemplo, \(n \geq 1000\)).

Las muestras bootstrap pueden crearse fácilmente con rsample::bootstraps(), como se ilustra a continuación.

bootstraps(Madrid_Sale_num_sample_bin, times = 10)

Si se usa la función trainControl(), se debe especificar: method = "boot".

10.5 Compensación (trade off) entre sesgo y varianza

En el entorno predictivo, el objetivo es que el error de predicción, en términos generales o por término medio, sea lo más pequeño posible. Sin embargo, no se pueden promediar los errores porque se compensarían los positivos con los negativos. Por ello, se promedian elevados al cuadrado (considerando solo su magnitud), denominándose dicho promedio “error cuadrático medio”, ECM (en este caso, de predicción): \(E(y_j- \hat y_j)^2\) en términos probabilísticos, o \(\sum _{j=1}^ {N}(y_j- \hat y_j)^2 \frac {n_j}{N}\) en términos descriptivos. Pues bien, el ECM se puede descomponer como suma de dos componentes:

• Uno debido a la diferencia entre el valor correcto de la variable objetivo o respuesta y el que se espera que proporcione el modelo. Dicha diferencia se denomina sesgo (en ingés, bias), y aparece elevado al cuadrado en dicha descomposición.
• Otro debido a que, dado un conjunto de valores de las variables predictoras, la respuesta del modelo no es siempre la misma. Esta variabilidad aparece en la descomposición en forma de varianza, y por ello se denomina varianza del error de predicción o, simplemente, varianza de predicción.

Lógicamente, el incremento/reducción de uno de los componentes implica la reducción/incremento del otro.

Un sesgo muy elevado es un indicador de que el modelo es muy simple y no ha ajustado bien los datos de entrenamiento (underfitting), lo cual se traduce en errores de predicción elevados. Una varianza de predicción elevada (es decir, pequeños cambios en los datos de entrada que producen salidas muy distintas), es un signo de complejidad en el modelo y sobreajuste (overfitting) de los datos de entrenamiento.

Los algoritmos con tendencia a un elevado porcentaje del ECM debido al sesgo tienen, lógicamente, un porcentaje del ECM debido a la varianza de predicción pequeño; es decir, tienen los problemas que se derivan del infraajuste de los datos: malas predicciones (sesgadas) y, encima, muy precisas. Y al contrario, aquellos que tienen un porcentaje del ECM debido al sesgo pequeño, tienen un porcentaje del ECM por varianza de predicción elevado.

Los modelos lineales (regresión lineal, análisis discriminante lineal, regresión logística…) suelen tener errores por sesgo elevados.⁸⁴ Modelos como los árboles de decisión, el k-vecinos más cercanos y los support vector machine tienen errores por sesgo pequeños (y, por tanto, varianza de predicción grande, siempre en relación al ECM total), son muy adaptables y ofrecen una flexibilidad extrema en cuanto a los patrones a los que pueden ajustarse. Sin embargo, plantean sus propios problemas, especialmente el de sobreajuste de los datos de entrenamiento, cuya consecuencia es que el modelo no se generalizará bien con datos nuevos.⁸⁵

Lógicamente, el modelo predictivo o clasificador deseado es el que tenga el menor ECM posible.⁸⁶ Si este no fuera el caso, habría que encontrar la combinación sesgo cuadrático-varianza de predicción que minimizase el ECM. La Fig. 10.4 se ha generado a partir de datos sintéticos de sesgo (al cuadrado) y varianza de predicción. En ella se puede apreciar que el valor mínimo del ECM es la suma de los valores del sesgo cuadrático y varianza de predicción determinados por la línea vertical amarilla.

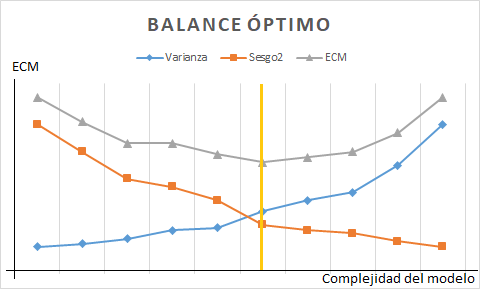
Figura 10.4: Trade off entre sesgo y varianza.

10.6 Ajuste de hiperparámetros

Los denominados “hiperparámetros” de un modelo son los valores de las configuraciones utilizadas durante el proceso de entrenamiento. A diferencia de los parámetros, son valores que no se obtienen a partir de los datos, sino que los propone el científico de datos. Podría decirse que son conjeturas (buenas conjeturas) realizadas sin utilizar las observaciones disponibles.

Los hiperparámetros, a diferencia de los parámetros, se fijan antes del entrenamiento. Siendo más específicos, al entrenar un modelo de aprendizaje automático se fijan los valores de los hiperparámetros para que con estos se estimen los parámetros. Podría decirse que son los ajustes del modelo para que este pueda resolver de manera óptima el problema de aprendizaje automático.

Algunos ejemplos de hiperparámetros utilizados para entrenar los modelos son la ratio de aprendizaje en el algoritmo del descenso del gradiente, el número de vecinos en el algoritmo de k-vecinos más cercanos, la profundidad máxima en un árbol de decisión, el número de árboles en un bosque aleatorio (random forest)… Como puede apreciarse, sirven para controlar la complejidad de los algoritmos de aprendizaje automático y, por tanto, la compensación entre sesgo y varianza.

En conclusión, hiperparámetros y parámetros son conceptos bien diferentes.

A la luz de la definición de hiperparámetro, lo natural sería que el científico de datos lo fijase de acuerdo con su experiencia en el pasado en problemas similares, asignándole los mismos, o parecidos, valores. Sin embargo, existen métodos más sofisticados para resolver el problema de la “optimización de hiperparámetros”, es decir, de la obtención del conjunto óptimo de valores de los mismos que proporciona la configuración que, tras el entrenamiento, dará lugar a los mejores resultados. Entre estos procedimientos cabe destacar los siguientes por ser los que incorporan los algoritmos más populares:

• Optimización bayesiana: utiliza la moda para elegir qué hiperparámetros considerar, en función del rendimiento de las elecciones anteriores.

• Búsqueda en cuadrícula (grid search): prueba con todas las combinaciones posibles de la cuadrícula.

• Búsqueda aleatoria: muestrea y evalúa aleatoriamente conjuntos de una distribución de probabilidad específica.

• Optimización secuencial basada en modelos: son una formalización de la optimización bayesiana.

A modo de ejemplo, los dos hiperparámetros que más influencia tienen en un modelo de random forest (véase Cap. 28) son mtry (número de variables muestreadas aleatoriamente como candidatas en cada split) y ntree (número de árboles). Pues bien, a continuación, como viene siendo habitual, se utiliza el conjunto de datos Madrid_Sale_num_sample_bin para buscar el valor óptimo de mtry mediante la técnica de búsqueda en cuadrícula; se usa la métrica Accuracy (exactitud), que hace referencia a la proporción de predicciones correctas, véase Sec. 10.7.

control <- trainControl(method = "repeatedcv", number = 10, repeats = 3)
seed <- 7
metrica <- "Accuracy"
set.seed(seed)
mtry <- sqrt(ncol(Madrid_Sale_num_sample_bin))
tunegrid <- expand.grid(.mtry = mtry)

Nota

La implementación del algoritmo de random forest del paquete randomForest proporciona la función tuneRF(), que busca valores mtry óptimos dados los datos disponibles.

Se entrena el modelo y se observa que la mayor exactitud, 68,76%, se obtiene con un mtree de 2,449489.

rf_default <- train(price_bin ~ ., data = Madrid_Sale_num_sample_bin, method = "rf", metric = metrica, tuneGrid = tunegrid, trControl = control)
print(rf_default)
# Accuracy   
# 0.6876006  

10.7 Evaluación de modelos

La última fase del proceso de modelización contesta a las preguntas: ¿Cómo de bueno es el modelo entrenado? ¿Cómo de bien generaliza los (buenos) resultados obtenidos en la fase de entrenamiento a nuevos conjuntos de datos (datos out-of-sample)? Por ello, en este epígrafe se presentan las métricas más populares de rendimiento de modelos en los entornos de regresión (predicción) y clasificación.

En el entorno de regresión, es prácticamente imposible predecir valores exactos, y hay que conformarse con muy buenas aproximaciones a dichos valores exactos, por lo que las métricas que se utilizan para medir la bondad del modelo entrenado suelen estar basadas en la diferencia entre los valores reales y los que predice el modelo, es decir, en los errores de predicción. La medida natural sería la media de los errores de predicción, pero, para evitar la compensación de los errores positivos con los negativos, y puesto que el interés se centra en la magnitud de los errores y no en su signo, las métricas de evaluación más populares en el entorno de regresión son:

• Error cuadrático medio (ECM): es la más utilizada en tareas de regresión. Como se avanzó en la Sec. 10.5, se define como la media de las diferencias cuadráticas de entre los valores objetivo (\(y_j\)) y los predichos por el modelo (\(\hat{y}_i\)), evitando así la compensación de errores positivos y negativos. Su expresión es, por tanto, \(ECM=\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y}_i)^2\). Al considerar los errores de predicción al cuadrado, exacerba los errores grandes, por lo que hay que utilizar esta métrica con cuidado cuando se tengan valores anómalos en el conjunto de datos y no hayan sido tratados en las fases previas a la modelización y validación. En ese caso, incluso un modelo cuasiperfecto podría tener un ECM elevado. Si todos los errores son inferiores a la unidad hay un riesgo elevado de subestimar lo malo que es el modelo (en caso de que lo fuese).

• Error absoluto medio (EAM): es una alternativa al ECM que se define como la media del valor absoluto de los errores de predicción (para evitar compensaciones): \(EAM=\frac{1}{n}\sum_{i=1}^{n}|y_i-\hat{y}_i|\). Al no elevar al cuadrado, no magnifica los errores grandes, por lo que es menos sensible que el ECM a valores anómalos, si bien tampoco es recomendable en caso de que estos no hayan sido tratados previamente. Una ventaja que tiene es que su unidad de medida es la misma que la de la variable objetivo.

• Raíz cuadrada del error cuadrático medio (RECM): “deshace”, no en un sentido matemático, sino aproximadamente, la elevación al cuadrado de los errores en el ECM y, por consiguiente, viene dada en las mismas unidades que la salida del modelo, lo que la hace más interpretable. Su expresión es: \(RECM=+\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y}_i)^2}\).

• Coeficiente de determinación (\(\bf R^2\)): se define como \(R^2=1-\frac{\sum_{i=1}^{n}(y_i-\hat y_i)^2}{\sum_{i=1}^{n}(y_i-\bar y)^2}\) (véanse detalles adicionales en el Cap. 5 de Montero, 2007) y su campo de variación es [\(-\infty\), 1]. En la práctica totalidad de las situaciones reales toma valores entre 0 y 1, puesto que solo toma valores negativos cuando el modelo entrenado sea muy deficiente y prediga peor que cuando se establece como predicción la media de las salidas observadas, sean cuales sean los valores de los predictores. Obviando estas situaciones, y aquellas en las que la varianza de la variable de salida no se pueda descomponer en varianza debida al modelo y varianza debida al error (por ejemplo, en el caso de una regresión potencial),⁸⁷ \(R^2\) se puede interpretar como la reducción proporcional en el ECM que tiene lugar al predecir las salidas del modelo mediante los predictores (cualquiera que sea la función que los ligue con la salida) en vez de mediante la media de la variable output (que es la predicción óptima en ausencia de predictores). Mide, por tanto, lo bueno que es disponer de predictores para predecir los valores de la variable output o de salida; o, en otros términos, el porcentaje de varianza de la variable salida que explican los predictores a través del modelo que liga a ambos. Cuanto más cercano esté a la unidad, mejor es el modelo a efectos predictivos.

• Coeficiente de determinación ajustado (\(\bf R_{ajd}^2)\): una limitación importante del \(R^2\) es que su valor puede aumentarse artificialmente mediante la inclusión de más y más variables predictoras, pues la inclusión de las mismas o mantiene o mejora dicha métrica. Esta circunstancia puede dar lugar a confusión, pues el hecho de que un modelo utilice más variables predictoras que otro no quiere decir que sea mejor. El \(R_{ajd}^2\) corrige dicha circunstancia penalizando la complejidad del modelo, entendiéndose que un modelo es más complejo que otro si utiliza un mayor número de variables predictoras que ese otro. Su expresión viene dada por \(R_{ajd}^2=1-\left(\frac{n-1}{n-p-1}\right)\left(1-R^2\right)\), y su valor nunca supera el del \(R^2\).

• Deviance: es una métrica relacionada con la estimación de modelos (especialmente modelos lineales generalizados) por el método de la máxima verosimilitud. Compara, por cociente, la verosimilitud del modelo estimado con la del modelo saturado (aquel que tiene tantos parámetros como observaciones⁸⁸ y que, por tanto, tiene la máxima verosimilitud alcanzable). Mide el grado en el que un modelo explica la variabilidad en un conjunto de datos cuando se utiliza la estimación de máxima verosimilitud. En términos de log-verosimilitud (\(l\)) se define como \(D=2(l_{Modelo \hspace{0,1cm} saturado}-l_{Modelo \hspace{0,1cm} propuesto})\), y, lógicamente, cuanto menor es la deviance, mejor es el modelo.

• Raíz del error logarítmico cuadrático medio (RELCM): similar a RMSE, pero tomando logaritmos en los valores reales y predichos. De especial interés cuando lo que importa es la magnitud relativa (porcentual) de los errores. No se puede utilizar cuando la variable objetivo toma valores negativos. Para salvar la problemática de que la variable objetivo tome el valor cero, generalmente se agrega una constante a los valores reales y predichos de la variable salida antes de aplicar la operación logarítmica. Dependiendo del problema, se puede elegir otro tipo de constante. Su expresión viene dada por: \(RMSLE=\sqrt{\frac{1}{n}(log(y_i+1)-log(\hat{y}_i+1))^2)}\).

En este manual se usan estas medidas en repetidas ocasiones. Por ejemplo, en el Cap. 19 se ajusta la regresión ridge en el subconjunto de entrenamiento y se evalúa su ECM en el subconjunto de test.

ridge_pred <- predict(ridge.mod, s = 1e10, newx = x[test, ])
mean((ridge_pred - y.test)^2)

En el entorno clasificatorio, las salidas del modelo pueden ser de clase (tal es el caso de los algoritmos de máquinas de vectores soporte y k-vecinos más cercanos, por ejemplo) o de probabilidad (caso de la regresión logística, los bosques aleatorios, el AdaBoost…). Dado que pasar de salidas probabilísticas a salidas de clase consiste únicamente en fijar umbrales de probabilidad, y que algunos algoritmos ya proporcionan el paso de salidas de clase a salidas probabilísticas, en lo que sigue no se hará distinción entre ellas.

En dicho entorno clasificatorio, es muy frecuente el uso de la matriz de confusión, que compara las clases (niveles categóricos) reales con las predichas en el subconjunto de test (cuyos resultados se conocen). La Fig. 10.5 muestra un ejemplo de clasificación multiclase (en concreto, 3 clases) basado en el famoso conjunto de datos “Flor iris” de Fisher, que considera tres especies (Iris setosa, Iris virginica e Iris versicolor). La predicción de la clase a la que pertenece una flor se hace en función del largo y el ancho del sépalo y del pétalo.

En la diagonal ascendente figura el número de flores, de cada color, cuya clase ha sido correctamente predicha. Los elementos fuera de dicha diagonal indican las flores, de cada clase, que el clasificador utilizado ha clasificado erróneamente. Como puede apreciarse, 47 de las 50 flores iris que se consideran fueron bien clasificadas. Sin embargo, dicho clasificador clasificó una flor versicolor como virgínica, y dos virgínicas como versicolores.

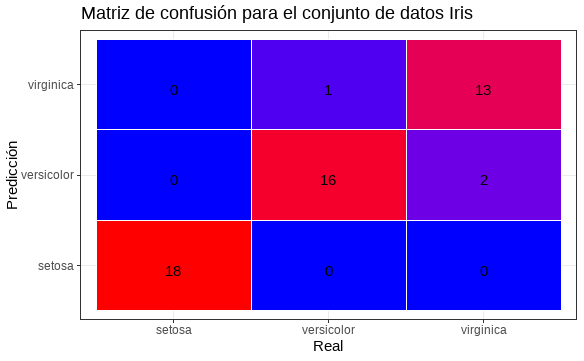
Figura 10.5: Matriz de confusión con tres clases.

Aunque el concepto de matriz de confusión es muy sencillo, la terminología que lo rodea no lo es tanto; incluso podría decirse que es confusa. La predicción proporcionada por el modelo puede ser (véase Fig. 10.6):

• Un verdadero positivo (VP): predicción de verdadero y verdadero en realidad.
• Un verdadero negativo (VN): predicción de falso y falso en realidad.
• Un falso positivo (FP): predicción de verdadero y falso en la realidad.
• Un falso negativo (FN): predicción de falso y verdadero en la realidad.

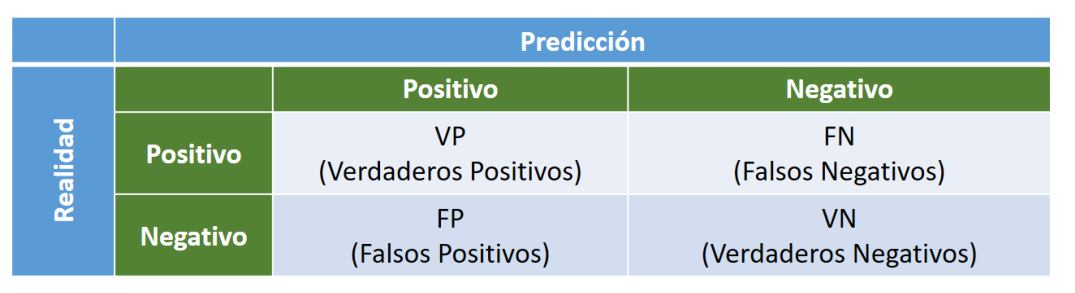
Figura 10.6: Terminología de una matriz de confusión.

Como se avanzó anteriormente, esta terminología es confusa y, por ello, se ilustra a continuación con un ejemplo. Supóngase que se está interesado en conocer si un determinado tratamiento médico tiene efectos positivos sobre una enfermedad. Echando mano de la teoría de la contrastación de hipótesis (véase Sec. 13.5), supóngase que se toma como hipótesis nula (\(H_0\)): SÍ y como hipótesis alternativa (\(H_1\)): NO. Pues bien:

• Si es cierto que el tratamiento en cuestión tiene un efecto positivo en la enfermedad y el modelo no rechaza la hipótesis nula, se tiene un VP.
• Si la hipótesis nula es falsa, es decir, si el tratamiento no tiene un efecto positivo sobre la enfermedad, y el modelo rechaza la hipótesis nula, entonces se tiene un VN.
• Si la hipótesis nula es falsa y el modelo concluye que no se rechaza la hipótesis nula de que el tratamiento cura la enfermedad, entonces se tiene un FP.
• Si es cierto que el tratamiento tiene un efecto positivo en la enfermedad y el modelo rechaza la hipótesis nula, se tiene un FN.

Las siguientes medidas se pueden calcular a partir de una matriz de confusión (es decir, a partir del número de VP, VN, FP y FN) para un clasificador binario:

• Exactitud. Es la proporción de predicciones correctas: \(Exactitud=\frac{VP+VN}{Total}\). Responde a la pregunta: ¿Con qué frecuencia funciona correctamente el clasificador? Lógicamente, la tasa de clasificación errónea se obtiene como \(\frac{FP+FN}{Total}\). En caso de desequilibrio notable de clase, por ejemplo, la clase A contiene 999 casos y la B tan solo 1, siendo B la clase rara, la clase positiva, la precisión no sería una métrica fiable para evaluar el rendimiento clasificatorio del modelo. Por ejemplo, el clasificador podría consistir en una regla que dijese que todos los casos pertenecen a la clase A, ¡y acertaría en el 99,9% de los casos! En estos casos, sería mejor utilizar como métricas la precisión y la sensibilidad.

• Precisión. Da respuesta a la pregunta: cuando el clasificador predice “SÍ”, ¿con qué frecuencia predice correctamente? Su expresión viene dada por: \(Precisión=\frac{VP}{VP+FP}\).

• Sensibilidad.⁸⁹ Restringe el denominador de la precisión a los SÍ reales. Responde a la pregunta: ¿cuando en realidad es un SÍ, cuál es el porcentaje de aciertos del clasificador? Su expresión es \(Sensibilidad=\frac{VP}{VP+FN}\). Por consiguiente, la sensibilidad es una medida de la probabilidad de que un caso real positivo se clasifique como positivo.

• Especificidad. Se define como \(Especificidad=\frac{VN}{FP+VN}\). Es, por tanto, el porcentaje de verdaderos negativos respecto de todo lo que debería haber sido clasificado como negativo. Su complementario, la 1-especificidad (\(\frac{FP}{FP+VN}\)) es, básicamente, una medida de la frecuencia (relativa) con la que se producirá una falsa alarma, o la frecuencia con la que un caso real negativo se clasifique como positivo.

• Puntuación F1. Es la media armónica de la precisión y la sensibilidad. Su campo de variación es [0, 1], donde 0 indica falta total de precisión y sensibilidad y 1 significa precisión y sensibilidad perfectas. La puntuación F1 penaliza los valores extremos y se suele utilizar en caso de conjuntos de datos desequilibrados.

• Área bajo la curva de características operativas del receptor (área bajo la curva ROC). Al graficar la sensibilidad (tasa de verdaderos positivos) frente a la tasa de falsos positivos (también denominada 1-especificidad), se obtiene la curva ROC. La diagonal ascendente representa la aleatoriedad. Cuanto más grande sea el área bajo la curva ROC, mejor será la precisión obtenida. Es una medida recomendable en el caso de clases desequilibradas. Un ejemplo de área bajo la curva ROC puede verse en el Cap. 16, y se reproduce en la parte derecha de la Fig. 10.7.

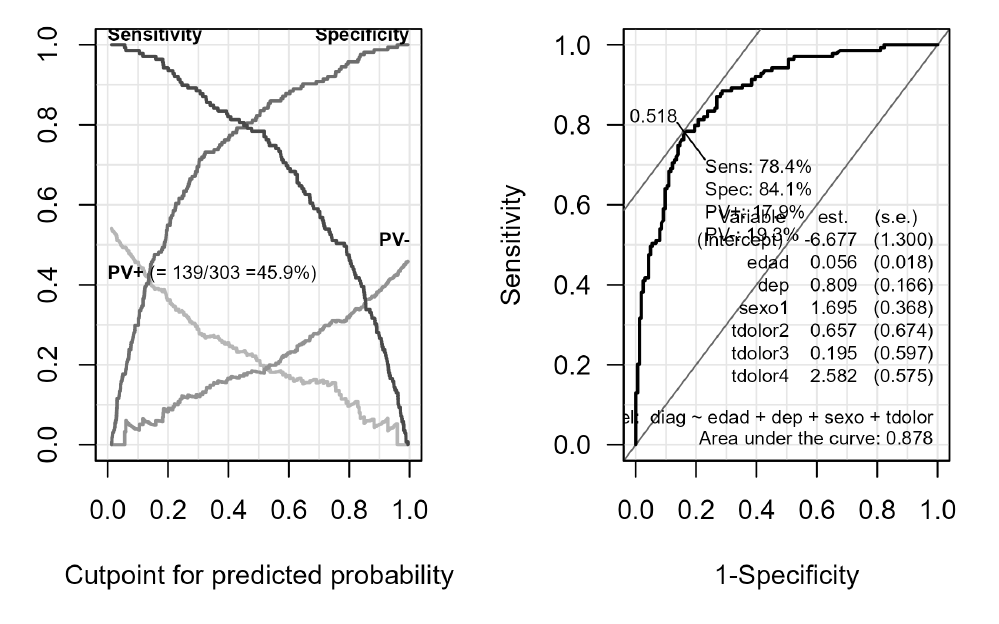
Figura 10.7: Ejemplo de curva ROC a partir de la estimación de un modelo lineal generalizado (parte derecha).

• Índice de Gini. Bien conocido en la literatura estadística sobre concentración, se trata de un indicador útil en el caso de clases desequilibradas. Su campo de variación es [0, 1], donde 0 representa la igualdad perfecta y 1 la concentración en una única clase. Puede calcularse a partir del área bajo la curva ROC de la siguiente manera: \(IG=2\hspace{0,1cm} \acute{A}rea\hspace{0,1cm} bajo \hspace{0,1cm} la\hspace{0,1cm}curva\hspace{0,1cm} ROC-1\). En caso de IG = 0, el área bajo la curva ROC es 1/2 y la curva ROC coincide con la diagonal ascendente. En caso de IG = 1, el área bajo la curva ROC será 0 y dicha curva vale 0 para todos los valores del eje de abscisas, excepto para el último, para el cual vale 1. En caso de que las observaciones no se vayan acumulando de una en una para la configuración de la curva bajo ROC, o para el cálculo directo del índice de Gini, es mejor utilizar una versión del mismo denominada “índice E” (IE, véase Cap. 3 de Montero, 2007), pues el índice de Gini tan solo proporcionará una aproximación de la concentración existente; buena aproximación, pero aproximación.

• Índice de Jaccard. Mide las similitudes entre el conjunto clases reales y predichas por el clasificador. Se define como el cociente entre el número de coincidencias en los conjuntos real y predicho (clases predichas correctamente) y el tamaño de la unión de los dos conjuntos (el doble del número de clases a etiquetar menos el número de clases predichas correctamente): \(I_{Jaccard}=\frac{VP+VN}{2Total-(Fp+FN)}\).

Otras medidas de interés son la pérdida logarítmica, el coeficiente de correlación de Matthews, el gráfico de Kolmogorov-Smirnov y el gráfico de ganancia y elevación. Estas, entre otras, pueden verse en Dembla (2020), Hernández-Orallo et al. (2011) y Vujović (2021), entre otros.

Con tantas métricas, ¿cómo decidir entre ellas? Será el conocimiento de la problemática que se esté estudiando (el negocio) el que normalmente guíe la elección de la métrica: si se trata de un problema de predicción de la producción de un determinado bien cuyo coste de almacenaje es elevado, lo más prudente sería utilizar el ECM para penalizar la sobreproducción; si lo que interesa son valores altos de la precisión y la sensibilidad (tal es el caso en numerosas situaciones del ámbito sanitario), la mejor medida sería la puntuación F1. No obstante, se habrá de tener siempre en cuenta que la exactitud, la precisión, la sensibilidad, la especificidad y el índice de Jaccard son buenas formas de evaluar clasificadores cuando las clases están equilibradas. En caso contrario, el área bajo la curva ROC y el IG (o el IE) son dos buenas alternativas.

Resumen

• En este capítulo se describen una serie de herramientas necesarias para desarrollar proyectos de ciencia de datos. Son herramientas que se utilizan se utilizan pre o postmodelado de los datos y que aumentan significativamente el rendimiento de los modelos. Tal caja de herramientas incluye el particionado del conjunto de datos, el manejo de datos no equilibrados, los métodos de remuestreo, el equilibrio entre sesgo y varianza, el ajuste de hiperparámetros y la evaluación de modelos, entre otras.

• Se hace especial hincapié en las métricas para evaluar modelos, tanto en el entorno de regresión como en el de clasificación, y, en ambos casos, se ofrece un amplio abanico de ellas.

• A efectos ilustrativos, se utilizan, fundamentalmente, el paquete caret y conjuntos de datos derivados del dataset Madrid_Sale.