Capítulo 42 Modelos econométricos espaciales

Andrés Vallone\(^{a}\) y Coro Chasco\(^{b}\)

\(^{a}\)Universidad Católica del Norte
\(^{b}\)Universidad Autónoma de Madrid

42.1 La dependencia espacial

En muchas ocasiones, los fenómenos de estudio no son independientes del espacio geográfico en el cual se producen. Esta circunstancia es precisamente la que se pone de manifiesto en la primera ley de la geografía enunciada por Tobler (1970): “Todas las cosas están relacionadas entre sí, pero las cosas más próximas en el espacio tienen una relación mayor que las distantes” (Tobler, 1970, p. 236). Esta situación produce una violación del supuesto básico de independencia de las variables aleatorias requerido por el método de estimación de mínimos cuadrados ordinarios (MCO).

En este contexto, los estimadores MCO ya no son óptimos y, por tanto, los estadísticos de contraste \(t\) y \(F\) pueden llevar a conclusiones erróneas (Anselin, 1988). Por ello, es necesario encontrar la manera de incorporar el espacio geográfico en los procesos de modelización. En este capítulo se aborda esta cuestión, mostrando primero los métodos de exploración de datos espaciales, para luego presentar las formas de modelización de las relaciones espaciales y los métodos de estimación en presencia de dichas relaciones.

Los modelos econométricos espaciales se centran en manejar las situaciones de dependencia espacial. Existe dependencia espacial cuando lo que sucede en una localización \(i\) está influenciado por lo que sucede en una localización \(j\) y viceversa (Anselin, 2013). La dependencia espacial se traduce en que los valores de la variable en las localizaciones \(i\) y \(j\) con \(i\neq j\) están correlacionados entre sí, hecho que se conoce como autocorrelación espacial (Anselin, 2013). La autocorrelación espacial puede ser positiva, cuando las localizaciones con valores similares tienden a estar juntos (altos con altos, bajos con bajos), o negativa, cuando las unidades espaciales tienden a estar rodeadas de vecinos con valores diferentes. Los patrones espaciales formados por la existencia de autocorrelación se muestran en la Fig. 42.1. La ausencia de autocorrelación es lo que se entiende como aleatoriedad espacial (Anselin, 2013).

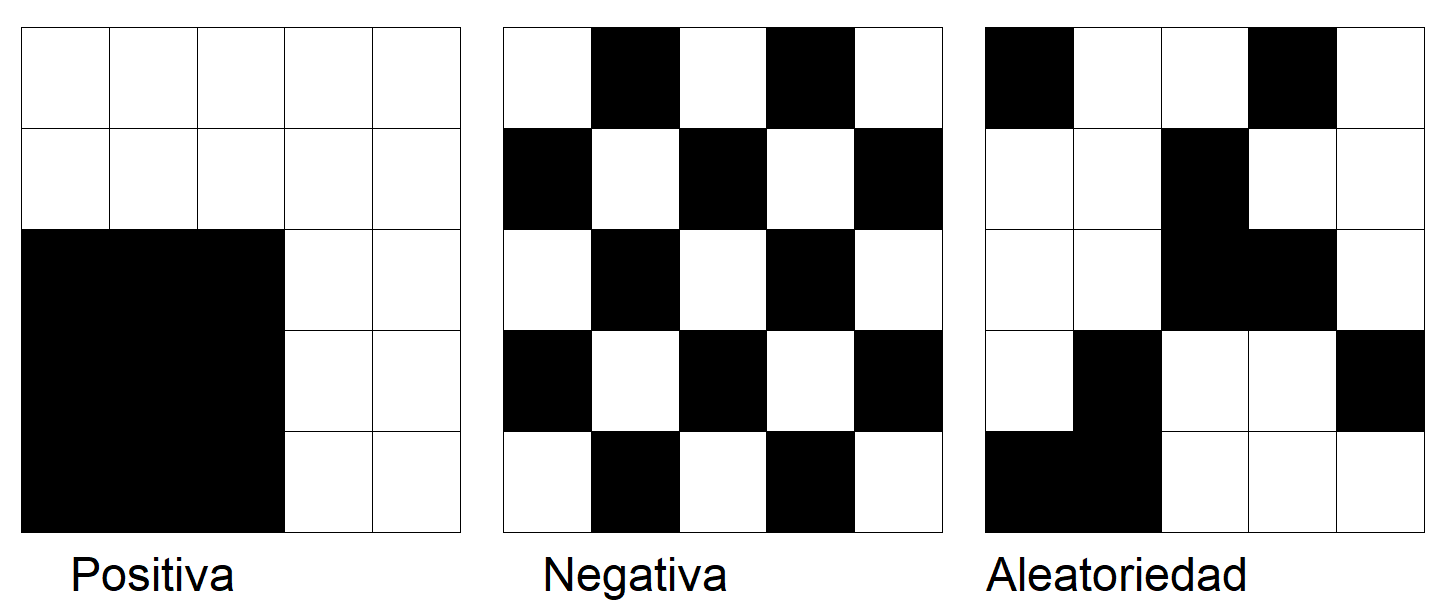
Figura 42.1: Patrones de autocorrelación espacial.

42.1.1 Modelización de las relaciones espaciales

El espacio puede jugar un rol importante en la configuración de los procesos a modelizar. Por ello, es necesario encontrar una forma de incorporar el espacio en los procesos de estimación. Para modelizar la interacción de una variable consigo misma es natural pensar en el concepto de autocorrelación. No obstante, a diferencia de la autocorrelación temporal, que es unidireccional (solo el pasado puede afectar el presente), en el caso del espacio la influencia es multidireccional en el entorno o vecindario de la localidad de análisis y, por tanto, es crucial definir el vecindario.

La matriz de vecindad o contigüidad \(\mathbf{W}_{n \times n}\) muestra la relación entre las \(n\) localidades analizadas, y por tanto, la interacción existente entre sí. Es una matriz simétrica y binaria, de forma que \(w_{ij} = 1\) si las localidades \(i\) y \(j\) son vecinas y cero si no lo son. Por tanto, \(w_{ii}=0\) puesto que una localidad no puede ser vecina de sí misma. Existen distintos criterios de definición de vecindad dependiendo del proceso que se desee modelizar y las características de los datos. Si se cuenta con un mapa de polígonos, entonces se puede utilizar alguno de los criterios que se presentan en la Fig. 42.2 para configurar la matriz \(\mathbf{W}\).

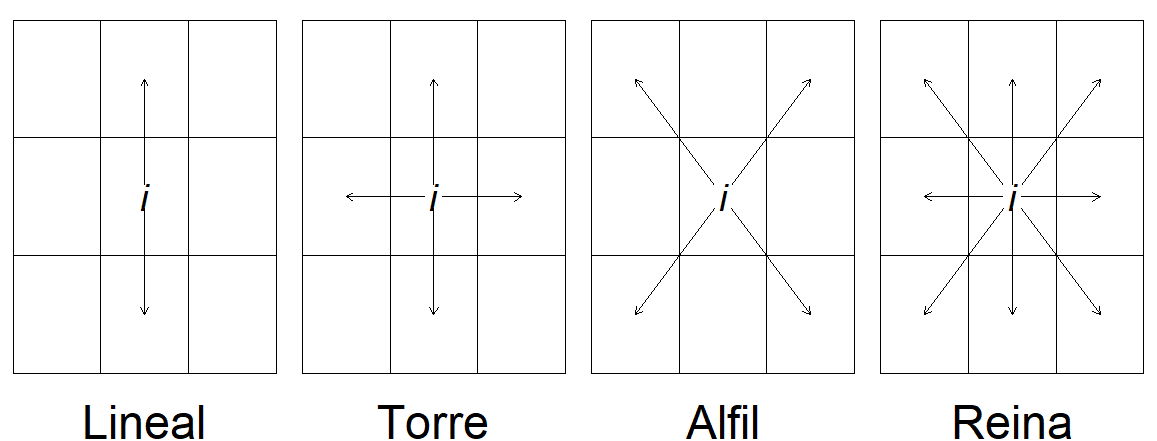
Figura 42.2: Criterios de vecindad.

Las matrices \(\mathbf{W}\) generadas bajo el criterio lineal consideran como vecinas a la localidad \(i\) todas aquellas localidades que compartan un borde situadas en la misma dirección cardinal, norte-sur o este-oeste, de esta localidad. El resto de los criterios de contigüidad siguen los movimientos de las piezas del ajedrez para definir la vecindad de la localidad \(i\). La construcción de una matriz de vecindad bajo el criterio de la torre implica considerar como vecinos de la localidad \(i\) aquellas localidades situadas al norte, sur, este u oeste y que compartan un borde con dicha localidad. El criterio de alfil considera como vecindad de la localidad \(i\) aquellas localidades situadas al noreste, noroeste, sureste o suroeste de la localidad \(i\) y que tengan, al menos, un punto en común. El criterio de la reina considera como vecindario de la unidad espacial \(i\) a las localidades, en cualquier dirección cardinal e intercardinal, que tengan al menos un punto en común con ella (Martori et al., 2008).

Dependiendo del fenómeno que se analice, la matriz de contigüidad puede ser construida considerando un vecindario más amplio; por ejemplo, considerando como vecinos de la localidad \(i\) a los vecinos de los vecinos de dicha localidad. En este caso se dice que la matriz de vecindad es de orden 2 (los vecinos y los vecinos de los vecinos). Las matrices \(\mathbf{W}\) se utilizan para capturar el efecto del vecindario a partir de medias ponderadas basadas en la cercanía de las unidades espaciales. Es por ello que las matrices de vecindad se estandarizan por filas. Los elementos de la matriz estandarizada se obtienen de la siguiente manera:

\[\begin{equation} w^e_{ij}=\frac{w_{ij}}{\sum_{j=1}^n w_{ij}}. \end{equation}\]

En palabras simples, cada elemento de cada fila de la matriz \(\mathbf{W}\) se divide por el total de dicha fila. Esto asegura que cada elemento de la matriz \(\mathbf{W}\) estandarizada se encuentre entre 0 y 1, y que la suma de cada una de sus filas sea siempre 1. Las matrices de vecindad estandarizadas llevan el nombre de matrices de pesos espaciales. A partir de ahora, cuando se haga relación a la matriz \(\mathbf{W}\) se estará haciendo referencia a una matriz de pesos espaciales.

Para el cálculo de las matrices de vecindad se utiliza el paquete spdep (Bivand, 2022). La función poly2nb() construye la relación de vecindad a partir de los polígonos de un objeto espacial según el criterio y el orden que se indique; la función nb2listw() transforma la relación de vecindad en una lista de pesos espaciales. Para ejemplificar la construcción de la matriz \(\mathbf{W}\), se utilizará el conjunto de datos del estudio de Guerry (1833). Esta base de datos contiene información respecto a estadísticas morales, criminales y sociales de las distintas provincias de Francia en 1830.²⁷³

library("spdep")
library("CDR")

reina <- poly2nb(guerry, queen = TRUE)
w_reina <- nb2listw(reina, style = "W", zero.policy = TRUE)
w_reina
#> Characteristics of weights list object:
#> Neighbour list object:
#> Number of regions: 85
#> Number of nonzero links: 420
#> Percentage nonzero weights: 5.813149
#> Average number of links: 4.941176
#>
#> Weights style: W
#> Weights constants summary:
#>    n  nn  S0     S1        S2
#> W 85 7225 85 37.2761 347.6683

En la salida anterior S0, S1 y S2 son constantes que se utilizan en los procesos inferenciales de los estadísticos de autocorrelación espacial global, como los tests I de Moran, C de Geary y G de Getis-Ord, entre otros.

Para construir una matriz de contigüidad de la torre de orden 1 se utilizan las mismas funciones, cambiando el parámetro queen de la función poly2nb():

torre <- poly2nb(guerry, queen = FALSE)
w_torre <- nb2listw(torre, style = "W", zero.policy = TRUE)

Cuando se trabaja con datos a escala puntual, o cuando existen situaciones geográficas de no contigüidad como, por ejemplo, una isla, la construcción de la matriz de contigüidad no es tan evidente. En estos casos, resulta más oportuno definir la matriz de vecindad a partir de criterios de distancia. Las matrices de \(\mathbf{W}\) basadas en distancias pueden tener configuraciones continuas de la matriz respecto a la distancia \(d\) entre las localidades \(i\) y \(j\), de tal manera que \(w_{ij}=1/d_{ij}\) o \(w_{ij}=1/d_{ij}^2\) y \(w_{ii}=0\). Otras configuraciones implican considerar un número \(k\) de vecinos más cercanos a cada localidad \(i\), de tal manera que:

\[\begin{align} \begin{cases} w_{ij}(k)=0 & i=j, \hspace{0,1cm}\forall k \\ w_{ij}(k)=1 & d_{ij} \leq d_i(k)\\ w_{ij}(k)=0 & d_{ij} > d_i(k) \end{cases} \end{align}\]

donde \(d_i(k)\) es la k-ésima menor distancia entre las localidades \(i\) y \(j\).

A continuación se calcula matriz de contigüidad basada en los 5 vecinos más próximos de las áreas urbanas chilenas con más de 2.000 habitantes. Para ello se utilizan funciones de Bivand (2022) y Pebesma (2018) y los datos de Vallone & Chasco (2020).

library("sf")
# Se extraen las coordenadas de las ciudades
coord <- st_coordinates(cities)
# Calcula la matriz vecindad de 5 vecinos más cercanos
w5knn <- knearneigh(coord, k = 5, longlat = T) |> knn2nb()

El uso de matrices de \(k\) vecinos próximos puede forzar la vecindad entre localidades, considerando vecinas a localidades que estén muy distantes entre sí. Para evitar este problema se puede usar una configuración de vecindad basada en una distancia límite \(d_{max}\), de tal manera que:

\[\begin{align} \begin{cases} w_{ij}=1 & d_{ij} \leq d_{max}\\ w_{ij}=0 & d_{ij} > d_{max}.\\ \end{cases} \end{align}\]

El problema de este criterio de vecindad es la posibilidad de generar unidades espaciales aisladas cuando \(d_{max}\) se fija en un valor muy bajo. Este problema se evita fijando la distancia máxima de tal manera que se asegure que todas las unidades espaciales tengan al menos un vecino.

# Calcula la k=1 matriz W
knn1 <- knearneigh(coord) |> knn2nb()
# Obtiene la distancia crítica
distancia_critica <- max(unlist(nbdists(knn1, coord)))
# genera la matriz de vecindad de distancia con w_ij distinto de cero para d_ij <= d_max
k1 <- dnearneigh(coord, 0, distancia_critica)
w_dist <- nb2listw(k1)

Debe considerarse que la configuración basada en \(k\) vecinos y en la distancia censurada dan lugar a matrices binarias, mientras que las matrices \(\mathbf{W}\) basadas en distancias no.

Para realizar el cálculo de la matriz \(\mathbf{W}\) basado en la distancia inversa (\(1/d_{ij}\)) se utilizará el mismo conjunto de datos que en las matrices \(\mathbf{W}\) basadas en distancias. No obstante, hay que tener en cuenta que: \((i)\) hay que utilizar una función decreciente respecto a la distancia (en este caso una hipérbola) para satisfacer la ley de Tobler (Tobler, 1970); y \((ii)\) dado que la incidencia que puede tener una localidad \(j\) que se encuentre muy lejana a la localidad \(i\) tiende a cero (Tobler, 1970), la matriz suele censurarse a una distancia máxima \(d_{max}\) a partir de la cual la incidencia entre unidades espaciales es nula. El criterio para la fijación de \(d_{max}\) es el mismo que el utilizado para evitar la existencia de unidades espaciales aisladas.

knn1 <- knearneigh(coord) |> knn2nb()
distancia_critica <- max(unlist(nbdists(knn1, coord)))
k1 <- dnearneigh(coord, 0, distancia_critica)
# Calcula la distancia entre los vecinos
dist_list <- nbdists(k1, st_coordinates(cities))
# Calcula la distancia inversa
i_dist_list <- lapply(dist_list, function(x) 1 / x)
# Crea la matriz W
w_dist_i <- nb2listw(k1, glist = i_dist_list, style = "W")

Se ha indicado anteriormente que la matriz \(\mathbf{W}\) se utiliza para capturar los efectos espaciales a partir de medias ponderadas, es decir, mediante la matriz \(\mathbf{W}\) se puede de construir el retardo espacial de una variable \(X\) sin más que multiplicar \(\bf{W}\) por \(\bf x\), el vector de observaciones de dicha variable. Por tanto, cada elemento del retardo espacial (o variable retardada espacialmente) \(\bf{Wx}\) es la media ponderada de las observaciones de la variable \(X\) en el vecindario de cada \(i\)-ésima localidad.

42.2 Medidas de autocorrelación espacial

Una buena herramienta para comprender las medidas de autocorrelación espacial es el diagrama de Moran (Anselin, 1996). El diagrama de Moran relaciona una variable con lo que sucede en su entorno mediante su retardo espacial en un gráfico de puntos. La Fig. 42.3 presenta un diagrama de Moran para la variable clergy del conjunto de datos Guerry. Esta variable hace referencia a la ratio de sacerdotes católicos sobre la población de cada provincia francesa. La línea horizontal discontinua en la Fig. 42.3 indica el promedio del retardo espacial, mientras que la línea vertical discontinua indica el promedio de la variable clergy. La división del diagrama de Moran a partir de dichos promedios genera cuatro zonas: \((i)\) el cuadrante superior derecho, que contiene las localidades en las que tanto en ellas como en su vecindario el valor de la variable clergy es superior al promedio correspondiente; \((ii)\) el cuadrante inferior izquierdo, en la que se ubican las localidades en las que tanto en ellas como en sus correspondientes vecindarios la variable clergy tiene valores inferiores a sus correspondientes promedios; \((iii)\) el cuadrante superior izquierdo, que contiene las localidades en las que el valor de la variable clergy es inferior al promedio, pero en su vecindario supera el valor promedio; y \((iv)\) el cuadrante inferior derecho, donde las localidades tienen un valor de la variable clergy superior al promedio de localidades, pero su vecindario no supera el valor promedio de los vecindarios.

A partir del diagrama de Moran es posible observar la situación de una variable respecto a su entorno. Si las localidades se sitúan mayoritariamente en los cuadrantes inferior izquierdo y superior derecho, las localidades con altos valores (superiores al promedio) de la variable de interés están rodeadas por localidades con altos valores de dicha variable, y las localidades con valores bajos (inferiores al promedio) están rodeadas de localidades con valores bajos, lo cual es una señal de existencia de autocorrelación espacial positiva. Si la concentración tiene lugar en los cuadrantes superior izquierdo e inferior derecho, la autocorrelación espacial es negativa.

library("spdep")
library("CDR")
w_reina_francia <- poly2nb(guerry, queen = TRUE) |>
  nb2listw()
## Diagrama de Moran
moran.plot(guerry$clergy, w_reina_francia,
  xlab = "Clergy",
  ylab = "Retardo espacial de Clergy"
)

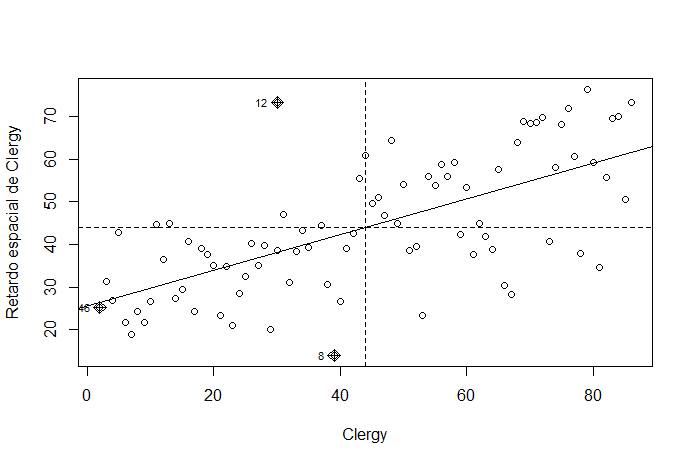
Figura 42.3: Diagrama de Moran de la variable Clergy.

En la Fig. 42.3 se pueden apreciar indicios de la existencia de autocorrelación positiva, es decir, las localidades francesas tienden a estar rodeadas de localidades con una ratio similar de clérigos. El diagrama de Moran es una herramienta gráfica. Para comprobar estadísticamente la existencia de autocorrelación espacial se utiliza el indicador \(I\) de Moran.

42.2.1 El indicador I de Moran

Sea una variable genérica \(X\). Sea \(Z=X- \bar{X}\) la variable \(X\) centrada. Entonces, el valor del indicador de Moran se obtiene como:

\[\begin{equation} I = \dfrac{n}{\sum_{i=1}^n\sum_{j=1}^n w_{ij}}\dfrac{\sum_{i=1}^{n}\sum_{j=1}^{n} z_{i}w_{ij}z_{j}}{\sum_{i=1}^{n}z_{i}^{2}}. \tag{42.1} \end{equation}\]

Su campo de variación es \([-1, 1]\) y el signo coincide con el tipo de autocorrelación: valores positivos son indicativos de autocorrelación positiva y valores negativos son indicadores de la existencia de autocorrelación negativa. Nótese que \(I\) no es sino el cociente entre la covarianza de la variable \(X\) y su retardo espacial y la varianza de la variable \(X\). Por tanto, coincide con el coeficiente de la regresión lineal del retardo espacial de \(X\) sobre la propia variable \(X\). La línea con pendiente positiva en la Fig. 42.3 es precisamente la recta de regresión del retardo espacial de clergy sobre la propia variable y, por tanto, su pendiente es el indicador \(I\) de Moran. En este sentido, cuanto mayor sea la pendiente de esta recta mayor será el grado de autocorrelación espacial existente. La significatividad estadística del indicador \(I\) se establece bajo la hipótesis nula de aleatoriedad espacial. La aleatoriedad espacial implica la inexistencia de autocorrelación espacial en la variable analizada; es decir, considera que la variable que se analiza está distribuida en forma aleatoria entre las localidades. En este contexto, \(p\)-valores bajos permiten rechazar la hipótesis de aleatoriedad espacial, indicando la existencia de autocorrelación espacial en la variable estudiada (Anselin, 2013).

moran.test((guerry$clergy), w_reina_francia,
  randomisation = TRUE,
  alternative = "two.sided"
)
#>
#> Moran I test under randomisation
#>
#> data: (guerry$clergy)
#> weights: w_reina_francia
#>
#> Moran I statistic standard deviate = 6.1632, p-value = 7.13e-10
#> alternative hypothesis: two.sided
#> sample estimates:
#> Moran I statistic       Expectation         Variance
#>       0.421118648      -0.011904762      0.004936422

Como puede apreciarse en la salida de R anterior, en el ejemplo de la variable clergy el \(p\)-valor permite rechazar la hipótesis nula de aleatoriedad espacial en favor de la existencia de autocorrelación positiva.

42.3 Modelos econométricos espaciales de corte transversal

Los modelos espaciales deben ser identificados antes de proceder a su estimación y contraste. Para ello, es importante disponer de una estrategia de identificación propia que permita al investigador estimar los parámetros poblacionales a partir de la observación de una muestra de datos.

Tradicionalmente, la econometría espacial ha resuelto este problema asumiendo que la especificación de los modelos es algo que se conoce a priori, bien a partir de la teoría económica existente o bien aplicando ciertas estrategias consistentes en la comparación de varios modelos competitivos. Dentro de esta última opción, se pueden destacar dos estrategias de modelización ampliamente utilizadas: \((i)\) la que va de lo particular (modelo básico sin efectos de autocorrelación espacial) a lo general (modelo con variables explicativas espacialmente retardadas) y \((ii)\) la que parte de un modelo general para terminar en un modelo de autocorrelación espacial más sencillo. A partir de estos dos enfoques previos es posible plantear la estrategia híbrida de Elhorst (2010).

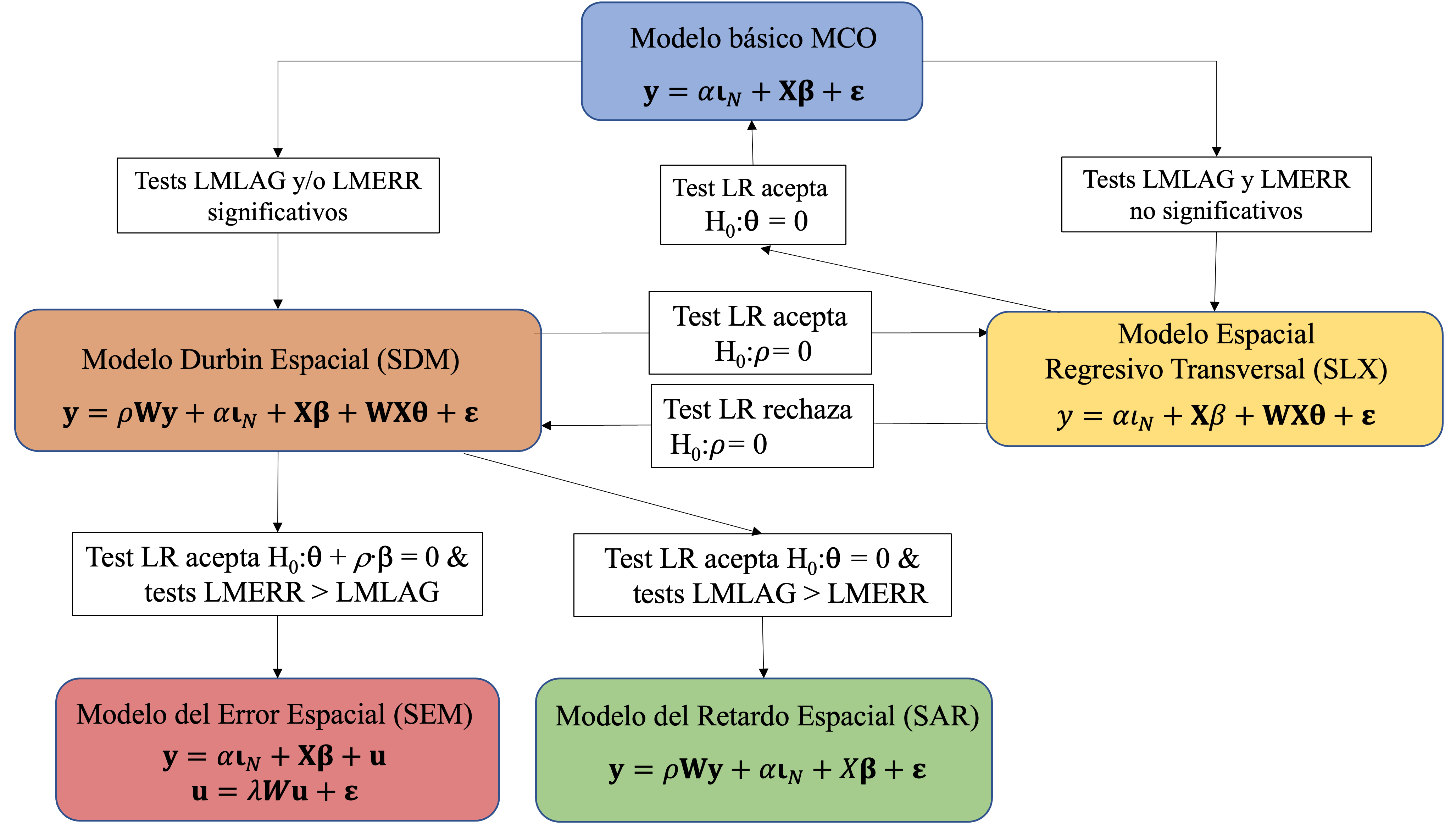
Figura 42.4: Estrategia de especificación híbrida Elhorst (2010).

Como puede verse en la Fig. 42.4, la estrategia híbrida comienza con la estimación de un modelo básico sin efectos espaciales:

\[\begin{equation} \mathbf{y} = \alpha \boldsymbol{\iota_n} + \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon}, \end{equation}\]

siendo \(\mathbf{y}\) el vector de observaciones de la variable dependiente, de orden \((n\times 1)\); \(\mathbf{X}\) la matriz que contiene los valores de las variables explicativas, de orden \((n\times k)\); \(\boldsymbol{\iota_n}\) un vector formado por 1, de orden \((n \times 1)\); \(\alpha\), \(\boldsymbol{\beta}\) son el conjunto de \((p+1)\) parámetros a estimar; y \(\boldsymbol{\epsilon}\) es el vector de perturbaciones aleatorias, de orden \((n\times 1)\), que se distribuye como \(\boldsymbol{\epsilon} \sim N(\mathbf{0},\sigma_{\epsilon}\mathbf{I}_n)\), siendo \(\mathbf{I}_n\) la matriz identidad de orden \(n\).

Este modelo se estima por MCO y luego se llevan a cabo dos contrastes del multiplicador de Lagrange (LM) sobre los errores de la regresión para contrastar si son ruido blanco desde el punto de vista espacial. Se trata de dos tests orientados a una única hipótesis alternativa cada uno de ellos: el LMLAG, para la hipótesis de variable dependiente espacialmente retardada, y el LMERR, para la hipótesis de dependencia residual. La hipótesis nula (el modelo básico MCO es válido) se rechaza si alguno de los estadísticos de contraste, que se distribuyen como una Chi cuadrado con 1 grado de libertad (\(\chi_1^2\)) bajo la hipótesis nula, resulta estadísticamente significativo. En este caso, se recomienda seleccionar el modelo Durbin espacial (SDM), que es un modelo general (Anselin, 1988):

\[\begin{equation} \mathbf{y} = \rho \mathbf{Wy} + \alpha \boldsymbol{\iota_n} + \mathbf{X}\boldsymbol{\beta} + \mathbf{WX}\boldsymbol{\theta} +\boldsymbol{\epsilon}, \end{equation}\]

siendo \(\rho\) un parámetro autorregresivo espacial y \(\boldsymbol{\theta}\) un vector de p parámetros autorregresivos espaciales.

Este modelo general incluye dos tipos de interacción espacial: los efectos endógenos (\(\mathbf{Wy}\)) y exógenos (\(\mathbf{WX}\)). La variable endógena espacialmente retardada (cuyos valores son los componentes del vector \(\mathbf{Wy}\)) referida al mismo momento del tiempo que la variable dependiente (con vector de valores \(\mathbf{y}\)) produce una situación de simultaneidad y, por tanto, de sesgo, ineficiencia e inconsistencia en los estimadores MCO. Por eso se recomienda su estimación por el método de máxima verosimilitud (maximum likelihood en inglés, ML), que supone normalidad en la distribución de los errores (véase Anselin, 1988, Cap. 6).

La estimación ML de este modelo permite utilizar la ratio de verosimilitud (likelihood ratio en inglés, LR) para contrastar, por separado, las hipótesis nulas \(H_0 (\boldsymbol{\theta}=0)\) y \(H_0(\rho=0)\), siendo las hipótesis alternativas las opciones contrarias. Dicho estadístico, bajo la hipótesis nula, se distribuye como una Chi cuadrado con \(k\) grados de libertad. En este punto, se pueden dar tres casos:

1. Si no se rechaza la primera hipótesis, pero sí la segunda, siempre y cuando los valores de los tests LMLAG > LMERR, el SDM debería simplificarse a un modelo del retardo espacial o modelo autorregresivo espacial de orden 1 (SAR):

\[\begin{equation} \mathbf{y} = \rho \mathbf{Wy} + \alpha \boldsymbol{\iota_n} + \mathbf{X}\boldsymbol{\beta} +\boldsymbol{\epsilon}. \tag{42.2} \end{equation}\]

Este modelo se estima por ML si los residuos de la estimación por MCO se distribuyen como una normal.

2. Si no se rechaza la segunda hipótesis, pero sí la primera, y los valores de los tests LMERR > LMLAG, debería seleccionarse el modelo del error espacial (SEM):

\[\begin{equation} \begin{cases} \mathbf{y} = \alpha \boldsymbol{\iota_n} + \mathbf{X}\boldsymbol{\beta} +\mathbf{u}\\ u=\lambda\mathbf{W}\boldsymbol{\epsilon} + \boldsymbol{\epsilon}, \end{cases} \end{equation}\]

siendo \(\lambda\) un parámetro autorregresivo espacial a estimar. La estimación MCO produciría estimadores insesgados y consistentes, pero ineficientes. Por eso, se considera aceptable estimar el modelo SEM por MCO realizando una inferencia robusta de la matriz de varianzas y covarianzas de los estimadores por el método KP-HET propuesto por Kelejian & Prucha (2010), que tiene en cuenta la existencia conjunta de heterocedasticidad y autocorrelación espacial en los residuos de la regresión.

3. Si se rechazan ambas hipótesis nulas o no hubiera consenso entre los resultados del test LR y los tests LM, entonces el SDM sería el modelo que mejor describiría los datos.

En segundo lugar, si tras la estimación MCO del modelo básico ninguno de los tests LM fuera estadísticamente significativo, entonces dicho modelo tendría que ser reestimado como un modelo espacial regresivo transversal (SLX):

\[\begin{equation} \mathbf{y} = \alpha \boldsymbol{\iota_n} + \mathbf{X}\boldsymbol{\beta} + \mathbf{WX}\boldsymbol{\theta} +\boldsymbol{\epsilon}. \end{equation}\]

Este modelo puede estimarse por MCO, ya que si las variables explicativas son exógenas también lo serán sus correspondientes retardos espaciales. Este modelo puede considerar todas las variables exógenas espacialmente retardadas o un subconjunto de ellas. Si la hipótesis de nulidad de los retardos espaciales de todas ellas fuese rechazada, debería elegirse el modelo básico como el que mejor describe los datos, es decir, no existiría evidencia alguna de la necesidad de efectos de autocorrelación espacial para explicar la variable dependiente. Pero si, por el contrario, la hipótesis \(H_0(\boldsymbol{\theta}=0)\) no fuese rechazada, habría que estimar el modelo SDM con las variables \(\mathbf{WX}\) estadísticamente significativas para contrastar, de nuevo, la hipótesis nula \(H_0(\rho=0)\). Si se rechaza esta hipótesis, el modelo seleccionado sería el SDM, pero en caso contrario, sería el modelo SLX el que mejor describiría los datos.

Estos modelos pueden estimarse también con metodología bayesiana utilizando el enfoque Markov Chains Monte Carlo (MCMC), tal y como se explica en LeSage & Pace (2009) Cap. 5.

El siguiente conjunto de secuencias de código muestra cómo estimar los modelos que intervienen en la estrategia de modelización de Elhorst. Para ello, se utiliza un conjunto de datos de los 120 municipios grandes de España (capitales de provincia y ciudades con población superior a 50.000 habitantes) que forman parte de las áreas urbanas del país (Mella & Chasco, 2006). Con estos datos se formula un modelo de crecimiento económico urbano en España en el que la tasa media de variación del PIB per cápita, en logaritmos, durante el período 1985-2003 (LPGH), se explica en función del PIB per cápita en logaritmos de 1985 (LGH85), la tasa de variación del número de entidades bancarias en el período 1985-2003 (BANK), el porcentaje de personas con educación secundaria y universitaria sobre la población de 16 y más años en el año 2001 (UNI01) y la tasa del número de patentes por habitante en el año 2000 (PAT00).

library("spatialreg")
library("tseries")

# Matriz de pesos espaciales
coord <- st_coordinates(gdpmap)
k6 <- knearneigh(coord, k = 6)
dmins <- knn2nb(k6) |> nb2listw(style = "W")
# Estimación modelo básico por MCO
gdp_ols <- lm(LPGH ~ LGH85 + BANK + UNI01 + PAT00, data = gdpmap)
summary(gdp_ols)
jarque.bera.test(gdp_ols$res) # Test normalidad de residuos
lm.LMtests(gdp_ols, dmins, test = "all") # Grupo de tests LM

# Estimación modelo SDM por ML
gdp_sdm <- lagsarlm(LPGH ~ LGH85 + BANK + UNI01 + PAT00, data = gdpmap, listw = dmins, type = "mixed")
summary(gdp_sdm)

# Estimación modelo SAR por ML
gdp_sar <- lagsarlm(LPGH ~ LGH85 + BANK + UNI01 + PAT00, data = gdpmap, listw = dmins)
summary(gdp_sar)
LR.Sarlm(gdp_sdm, gdp_sar) # Test LR: SDM vs. SAR

# Estimación del modelo SEM por ML
gdp_err <- errorsarlm(LPGH ~ LGH85 + BANK + UNI01 + PAT00, data = gdpmap, listw = dmins, tol.solve = 1e-16)
summary(gdp_err)
LR.Sarlm(gdp_sdm, gdp_err) # Test LR: SDM vs. SEM

# Estimación del modelo SLX por MCO

# Cálculo retardos espaciales
gdpmap$WLGH85 <- lag(dmins, gdpmap$LGH85)
gdpmap$WBANK <- lag(dmins, gdpmap$BANK)
gdpmap$WUNI01 <- lag(dmins, gdpmap$UNI01)
gdpmap$WPAT00 <- lag(dmins, gdpmap$PAT00)

gdp_slx <- lm(LPGH ~ LGH85 + BANK + UNI01 + PAT00 + WLGH85 + WBANK + WUNI01 + WPAT00, data = gdpmap)
summary(gdp_slx) # Modelo SLX completo

gdp_slx2 <- lm(LPGH ~ LGH85 + BANK + UNI01 + PAT00 + WLGH85 + WPAT00, data = gdpmap)
summary(gdp_slx2) # Modelo SLX parsimonioso
LR.Sarlm(gdp_sdm, gdp_slx2) # Test LR: SDM vs. SLX

42.3.1 Estimación SAR

A continuación se muestra la salida de la estimación del modelo SAR, pudiéndose observar que todos los parámetros estimados, incluido \(\rho\), son estadísticamente significativos.

library("CDR")
library("spatialreg")
library("tseries")
library("spdep")

# Matriz de pesos espaciales
coord <- st_coordinates(gdpmap)
k6 <- knearneigh(coord, k = 6)
dmins <- knn2nb(k6) |> nb2listw(style = "W")
# Estimación modelo SAR por ML
gdpsar <- lagsarlm(LPGH ~ LGH85 + BANK + UNI01 + PAT00,
  data = gdpmap,
  listw = dmins
)
summary(gdpsar)

#> Call:lagsarlm(formula = LPGH ~ LGH85 + BANK + UNI01 + PAT00, data = gdpmap,
#> listw = dmins)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.0184657 -0.0034523 0.0012278 0.0032544 0.0194746
#>
#> Type: lag
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 2.5745e-01 3.0703e-02 8.3851 < 2.2e-16
#> LGH85 -3.2962e-02 4.4472e-03 -7.4119 1.246e-13
#> BANK 6.6493e-05 1.3086e-05 5.0811 3.753e-07
#> UNI01 4.6884e-04 8.4080e-05 5.5762 2.459e-08
#> PAT00 4.7256e-02 1.8113e-02 2.6090 0.009082
#>
#> Rho: 0.36545, LR test value: 16.353, p-value: 5.2578e-05
#> Asymptotic standard error: 0.078929
#> z-value: 4.6302, p-value: 3.6538e-06
#> Wald statistic: 21.438, p-value: 3.6538e-06
#>
#> Log likelihood: 447.309 for lag model
#> ML residual variance (sigma squared): 3.7602e-05, (sigma: 0.006132)
#> Number of observations: 122
#> Number of parameters estimated: 7
#> AIC: -880.62, (AIC for lm: -866.27)
#> LM test for residual autocorrelation
#> test value: 6.4996, p-value: 0.01079

42.3.2 Comparando SAR con SDM

A continuación se muestra el resultado del test comparando el modelo SDM con el SAR. A la luz de los valores de la LR se rechaza que \(\bf {\theta}=0\) sea cero y, por tanto, el modelo SDM es más adecuado para explicar esta variable que el modelo SAR.

# Matriz de pesos espaciales
coord <- st_coordinates(gdpmap)
k6 <- knearneigh(coord, k = 6)
dmins <- knn2nb(k6) |> nb2listw(style = "W")

# Estimación modelo SDM por ML
gdpsdm <- lagsarlm(LPGH ~ LGH85 + BANK + UNI01 + PAT00,
  data = gdpmap,
  listw = dmins, type = "mixed"
)

# Estimación modelo SAR por ML
gdpsar <- lagsarlm(LPGH ~ LGH85 + BANK + UNI01 + PAT00,
  data = gdpmap,
  listw = dmins
)

LR.Sarlm(gdpsdm, gdpsar) # Test LR: SDM vs. SAR

#> Likelihood ratio for spatial linear models
#>
#> data:
#> Likelihood ratio = 11.559, df = 4, p-value = 0.02095
#> sample estimates:
#> Log likelihood of gdpsdm Log likelihood of gdpsar
#> 453.0885 447.3090

42.3.3 Interpretación de los estimadores de los modelos de autocorrelación espacial

Solo en los modelos de autocorrelación espacial en los que el efecto endógeno (\(\mathbf{Wy}\)) no está presente en la parte derecha del modelo, los coeficientes estimados (\(\hat{{\bf\beta}}\)) pueden interpretarse de forma directa, como en el modelo básico sin efectos espaciales. Es decir, el efecto marginal en la variable explicada de un cambio del valor de una variable explicativa continua coincide con la estimación del coeficiente correspondiente a dicha variable, para todas y cada una de las localizaciones. Por ejemplo, para la \(k\)-ésima variable explicativa, en la \(i\)-ésima localización \(i=1,..., n\) se tiene:

\[\begin{equation} \frac{\partial Y_i}{\partial X_{i,k}}= \beta_k . \tag{42.3} \end{equation}\]

En los modelos SAR y SDM, la correcta interpretación de los estimadores implica pasar antes de su forma estructural a su forma reducida. Así, por ejemplo, en el modelo SAR la forma reducida de la expresión (42.2) sería (bajo ciertas condiciones de invertibilidad):

\[\begin{equation} \mathbf{y} = (\mathbf{I}-\rho\mathbf{W})^{-1}(\alpha \boldsymbol{\iota_n}+\mathbf{X}\boldsymbol{\beta}+\boldsymbol{\epsilon}). \tag{42.4} \end{equation}\]

El término \((\mathbf{I}-\rho\mathbf{W})^{-1}\) se denomina multiplicador espacial y, utilizando la expansión potencial, puede expresarse también del modo siguiente:

\[\begin{equation} (\mathbf{I}-\rho\mathbf{W})^{-1}=\mathbf{I}+\rho\mathbf{W}+\rho^2\mathbf{W}^2+\dots \end{equation}\]

Si se utiliza esta nueva expresión en la ecuación (42.4) se observa más claramente que el valor de \(Y\) en una determinada localización es función no solo del valor de las variables explicativas en esa localización, sino también del valor de las explicativas en las localizaciones vecinas (a través del término \(\rho\mathbf{WX}\boldsymbol{\beta}\)), del valor de las explicativas en las localizaciones vecinas a las vecinas (a través del término \(\rho^2\mathbf{W}^2\mathbf{X}\boldsymbol{\beta}\)), etc., hasta llegar a los límites del sistema espacial en estudio.

\[\begin{equation} E(Y|\mathbf{X})=\mathbf{X}\boldsymbol{\beta}+\rho\mathbf{W}\mathbf{X}\boldsymbol{\beta}+\rho^2\mathbf{W}^2\mathbf{X}\boldsymbol{\beta}+\rho^3\mathbf{W}^3\mathbf{X}\boldsymbol{\beta}+\dots \end{equation}\]

LeSage & Pace (2009) presentan el cambio (también llamado efecto o impacto) experimentado por \(\mathbf{y}\) en una localización \(i\), sea cual sea \(i\), debido a un cambio en el valor \(X_k\) en otra localización, \(j\), sea cual sea \(j\). Dicho conjunto de impactos o efectos se presenta en una matriz completa, \(\mathbf{S}_k(\mathbf{W})_{ij}\), de orden \(n\times n\). Así, cada variable explicativa \(X_k\) del modelo tendrá una matriz completa propia de impactos sobre la variable dependiente:

\[\begin{equation} \mathbf{S}_k(\mathbf{W})_{ij}=(\mathbf{I_n}-\rho\mathbf{W})^-1\beta_k . \end{equation}\]

donde el elemento de la i-ésima columna y la j-ésima fila de la matriz es \(\frac{\partial Y_j}{\partial X_{ik}}\), el impacto de un incremento en la variable \(X_k\) en la i-ésima localización sobre la variable \(Y\) en la j-ésima localización.

En los modelos SAR y SDM, también se puede distinguir entre efectos directos e indirectos. El efecto directo sería el efecto causado por cambios en el valor de \(X_k\), en una localización \(i\) sobre el valor de \(Y\) en esa misma localización. Estos efectos son los valores de la diagonal principal de la matriz, \(s_k(\mathbf{W})_{ii}\). El efecto indirecto viene dado por el resto de los valores de la matriz \(\mathbf{S}_k(\mathbf{W})_{ij}\), que serían los “bucles de retroalimentación” en los que el valor de \(X_k\), en una localización \(j\), afecta al valor de \(Y\) en la localización \(i \neq j\), y viceversa, pudiéndose dar recorridos más largos en los que el efecto en una localización podría llegar a la última localización observada \(n\) y luego volver de nuevo al punto de partida.

Por ejemplo, \(s_k(\mathbf{W})_{11}\) es el efecto directo de un cambio unitario en el valor de la variable \(X_k\) en la localización 1 (\(\mathbf{x}_{k1}\)) sobre el valor de la variable \(Y\) en esa misma localización (\(Y_1\)), mientras que el valor \(\mathbf{s}_k(\mathbf{W})_{12}\) es el efecto indirecto de un cambio unitario en el valor de la variable \(X_{k}\) en la primera localización, sobre el valor de la variable \(Y\) en la segunda (\(Y_2\)). En las filas, la matriz \(\mathbf{S}_k(\mathbf{W})_{ij}\) tiene los efectos de un cambio unitario en \(X_k\) en la \(i\)-ésima localización en la variable \(Y\) y en cada una de sus localizaciones. Las columnas de la matriz contienen el efecto de un cambio unitario en \(X_k\), en cada una de sus posibles localizaciones, sobre la variable \(Y_j\), provocado “desde” todas y cada una de las localizaciones \(i\) sobre la localización \(j\).

Dado que no es posible contrastar si todos los impactos directos e indirectos contenidos en la matriz \(\mathbf{S}_k(\mathbf{W})_{ij}\) son significativamente distintos de cero o construir intervalos de confianza para ellos, LeSage y Pace proponen llevar a cabo el proceso inferencial sobre el valor medio de los efectos directos y totales, extrayendo el promedio de los efectos indirectos por diferencia: \[\begin{align} \bar{M}(k)_{directo}=tr(\mathbf{S}_k(\mathbf{W}))/n \\ \bar{M}(k)_{total}=\boldsymbol{\iota'_n}\mathbf{S}_k(\mathbf{W})\boldsymbol{\iota_n}/n \\ \bar{M}(k)_{indirecto}=\bar{M}(k)_{total}- \bar{M}(k)_{directo}, \end{align}\]

donde \(\bar{M}\) indica que se trata de un efecto promedio.

El siguiente conjunto de secuencias sirve para calcular las matrices de efectos directos, indirectos y totales, así como la inferencia para los modelos SAR y SDM, en el caso de la modelización del crecimiento económico urbano en España.

library("coda")

# Cálculo de los efectos para el modelo SAR (LeSage y Pace)
Wsp <- as(as_dgRMatrix_listw(dmins), "CsparseMatrix")
trMat <- trW(Wsp, type = "mult")

set.seed(1234) # Simulaciones para el proceso inferencial
gdpsar_impacts <- impacts(gdpsar, tr = trMat, R = 1000)
summary(gdpsar_impacts, zstats = TRUE, short = TRUE)
HPDinterval(gdpsar_impacts, choice = "direct")
HPDinterval(gdpsar_impacts, choice = "indirect")
HPDinterval(gdpsar_impacts, choice = "total")
plot(gdpsar_impacts, choice = "direct")
plot(gdpsar_impacts, choice = "indirect")
plot(gdpsar_impacts, choice = "total")
plot(gdpsar_impacts, trace = TRUE, density = FALSE, choice = "total")

# Cálculo de la matriz de impactos para la variable LGH85
clear.pr <- rep(NA, dim(gdpmap)[1])
names(clear.pr) <- gdpmap$MUNICIPIO
svec <- rep(0, dim(gdpmap)[1])
eye <- matrix(0, nrow = dim(gdpmap)[1], ncol = dim(gdpmap)[1])
diag(eye) <- 1
for (i in 1:length(clear.pr)) {
  cvec <- svec
  cvec[i] <- 1
  res <- solve(eye - gdpsar[["rho"]] * Wsp) %*% cvec * gdpsar[["coefficients"]][["LGH85"]]
  clear.pr[i] <- res[i]
}
mult <- solve(eye - gdpsar[["rho"]] * Wsp)
deriv_LGH85 <- solve(eye - gdpsar[["rho"]] * Wsp) * gdpsar[["coefficients"]][["LGH85"]]

# Cálculo de los efectos para el modelo SDM (LeSage y Pace)
set.seed(1234) # Simulaciones para el proceso inferencial
gdpsdm_impacts <- impacts(gdpsdm, tr = trMat, R = 1000)
summary(gdpsdm_impacts, zstats = TRUE, short = TRUE)
HPDinterval(gdpsdm_impacts, choice = "direct")
HPDinterval(gdpsdm_impacts, choice = "indirect")
HPDinterval(gdpsdm_impacts, choice = "total")
plot(gdpsdm_impacts, choice = "direct")
plot(gdpsdm_impacts, choice = "indirect")
plot(gdpsdm_impacts, choice = "total")
plot(gdpsdm_impacts, trace = TRUE, density = FALSE, choice = "total")

42.3.4 Impacto del SDM

A continuación se presenta la salida del cálculo de los efectos para el modelo SDM (LeSage & Pace, 2009), pudiéndose observar que todos son estadísticamente significativos y, salvo en el caso de la variable LGH85, todos ellos son positivos. El signo negativo del coeficiente de LGH85 demuestra la convergencia en renta en el grupo de grandes ciudades españolas. El impacto total de un crecimiento del 10% del PIB per cápita en una ciudad en el período inicial (1985) supuso una caída de la tasa media de variación del PIB per cápita en el período 1985-2003 del \(-0,63\) % en dicha ciudad. Este impacto es la suma del efecto directo causado por el crecimiento del PIB per cápita en la propia ciudad (\(-0,43\)), que es el efecto directo, y el efecto indirecto proveniente del crecimiento del PIB per cápita en el resto de ciudades (\(-0,20\)). Por su parte, el efecto total del crecimiento de 10 patentes por habitante supuso un crecimiento del PIB per cápita en el período del \(2,12\) %, del cual un \(0,5\) % procedía del crecimiento de las patentes per cápita en la propia ciudad (efecto directo) y el \(1,62\) % restante fue causado indirectamente por el crecimiento de las patentes en el resto de ciudades.

# Cálculo de los efectos para el modelo SAR (LeSage y Pace)
Wsp <- as(as_dgRMatrix_listw(dmins), "CsparseMatrix")
trMat <- trW(Wsp, type = "mult")
set.seed(1234) # Simulaciones para el proceso inferencial
gdp_sdm_impacts <- impacts(gdpsdm, tr = trMat, R = 1000)
summary(gdp_sdm_impacts, zstats = TRUE, short = TRUE)
#> Impact measures (mixed, trace):
#> Direct Indirect Total
#> LGH85 -3.967704e-02 -1.656718e-02 -5.624422e-02
#> BANK 7.484574e-05 -3.878932e-05 3.605642e-05
#> UNI01 5.459202e-04 3.900067e-04 9.359269e-04
#> PAT00 5.029859e-02 1.621204e-01 2.124189e-01
#> ========================================================
#> Simulation results ( variance matrix):
#> ========================================================
#> Simulated standard errors
#> Direct Indirect Total
#> LGH85 4.835913e-03 1.205378e-02 1.208788e-02
#> BANK 1.289395e-05 4.475846e-05 4.830235e-05
#> UNI01 8.434442e-05 3.397464e-04 3.621312e-04
#> PAT00 2.037202e-02 1.317136e-01 1.441993e-01
#>
#> Simulated z-values:
#> Direct Indirect Total
#> LGH85 -8.246556 -1.3907437 -4.6859617
#> BANK 5.826543 -0.9252065 0.6980269
#> UNI01 6.504595 1.2126777 2.6527099
#> PAT00 2.454730 1.2664303 1.5035704
#>
#> Simulated p-values:
#> Direct Indirect Total
#> LGH85 2.2204e-16 0.16430 2.7865e-06
#> BANK 5.6587e-09 0.35486 0.4851604
#> UNI01 7.7903e-11 0.22525 0.0079848
#> PAT00 0.014099 0.20536 0.1326920

plot(gdp_sdm_impacts, choice = "direct")
plot(gdp_sdm_impacts, choice = "indirect")
plot(gdp_sdm_impacts, choice = "total")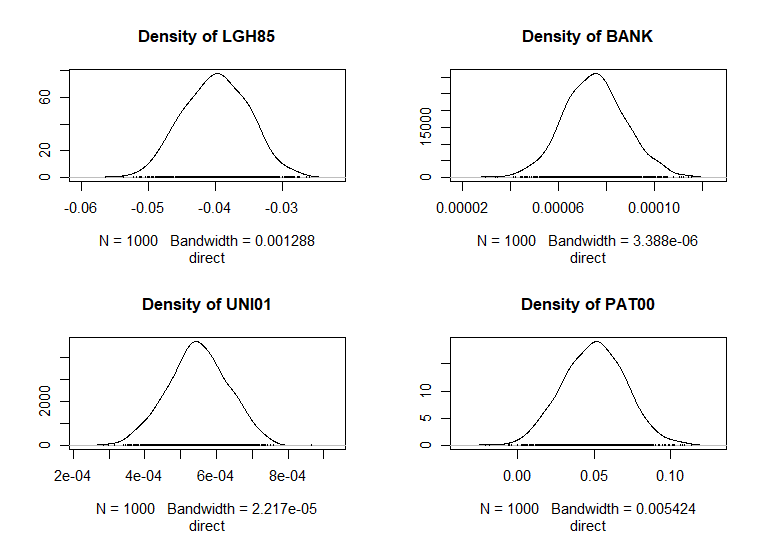

Figura 42.5: Impactos directos (SDM).

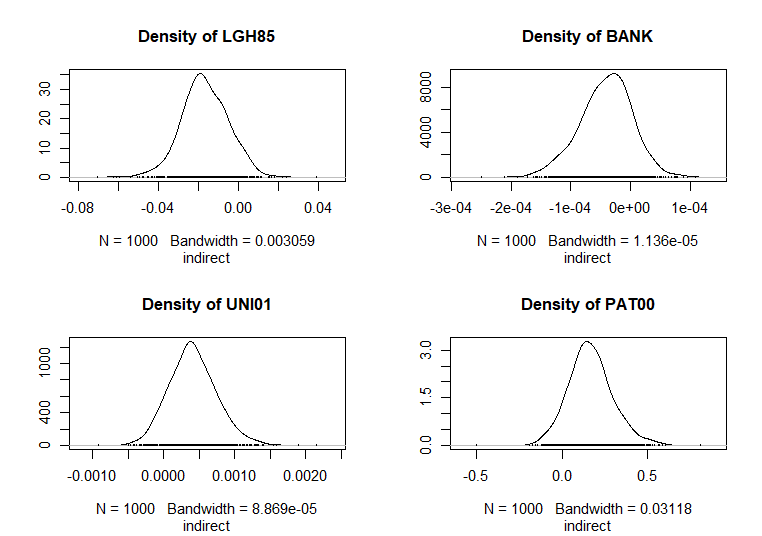
Figura 42.6: Impactos indirectos (SDM).

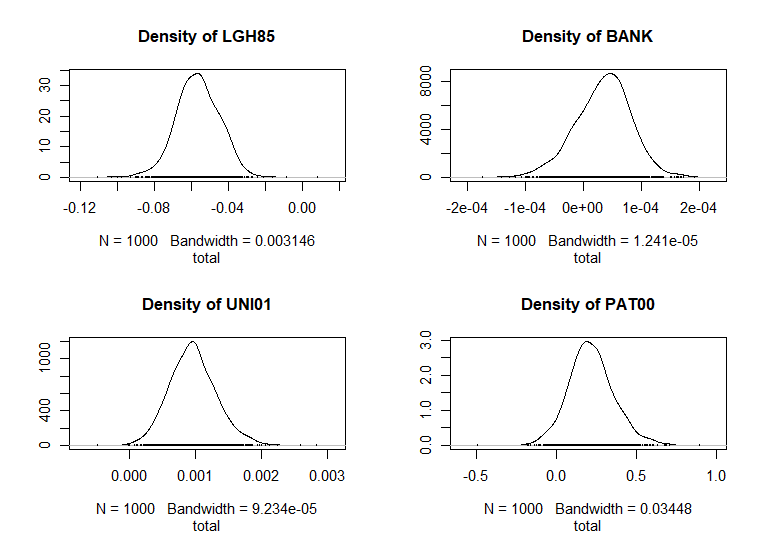
Figura 42.7: Impactos totales (SDM).

Como puede observarse en las Figs. 42.5, 42.6 y 42.7, para cada variable explicativa se estiman tres estimadores, de forma que el efecto total causado por el cambio unitario en el valor de dicha variable sobre el valor de la variable explicada, en una ciudad determinada, es la suma de dos efectos, uno directo, ocasionado por el cambio acaecido en la propia ciudad, y otro indirecto, proveniente del cambio acaecido en el resto de ciudades de España, existiendo tantos efectos como ciudades.

Resumen

• En este capítulo se introduce a la componente espacial en la estimación econométrica y, en particular, el efecto de dependencia espacial inherente en alguna de las variables involucradas en el proceso de modelización.

• Primero, se observa la heterogeneidad espacial de los datos a partir de los mapas temáticos y se presenta el indicador de autocorrelación espacial de Moran.

• Posteriormente, se construye la matriz de pesos espaciales bajo distintas especificaciones.

• Por último, se muestra la taxonomía de los modelos econométricos espaciales, presentando la estrategia de especificación híbrida y se procede a la interpretación de los coeficientes estimados.