Capítulo 43 Procesos de puntos

Jorge Mateu\(^{a}\) y Mehdi Moradi\(^{b}\)

\(^{a}\)Universidad Jaume I
\(^{b}\)Umeå Universitet

43.1 Introducción

La estadística espacial es una rama de la estadística que se ha desarrollado rápidamente durante los últimos treinta años, tanto en el plano teórico como en el práctico. A ello han contribuido, de manera significativa, la creciente disponibilidad de potencia computacional y variedad en software, que han estimulado la capacidad de resolver problemas cada vez más complejos. Lo cierto es que estos problemas tienen como elemento común la estructura espacial. En general, se ha observado un desarrollo científico notable en el campo de la estadística espacial: los nuevos problemas, bien definidos, con un carácter común, que saltaron a la agenda del investigador, y la disponibilidad de datos motivaron nuevos desarrollos teóricos.

La estadística espacial reconoce y explota las ubicaciones espaciales de los datos al diseñar, recopilar, administrar, analizar y mostrar dichos datos. Los datos espaciales suelen ser dependientes, por lo que se necesitan clases de modelos espaciales que permitan la predicción de procesos espaciales y la estimación de sus parámetros. Los patrones espaciales ocurren en una variedad sorprendentemente amplia de disciplinas científicas: los ecologistas estudian las interacciones entre plantas y animales, los silvicultores y agricultores deben investigar la capacidad de las plantas y tener en cuenta las variaciones del suelo en sus experimentos. Así pues, cualquier disciplina que trabaje con datos recopilados en diferentes ubicaciones espaciales necesita desarrollar modelos que indiquen cuándo hay dependencia entre mediciones en diferentes lugares y cómo llevar a cabo estimaciones y predicciones en presencia de dependencia espacial. Referencias modernas sobre estadística espacial incluyen los libros de Diggle (2013), N. Cressie & Wikle (2015), Montero et al. (2015), Wikle et al. (2019), Diggle & Giorgi (2019), entre otros.

Este capítulo se centra en los patrones espaciales de puntos. Datos en forma de conjunto de puntos distribuidos irregularmente dentro de una región del espacio surgen en muchos contextos diferentes; por ejemplo, localizaciones de incendios forestales (véase Fig. 43.1), delitos (véase Fig. 43.2), árboles en un bosque, nidos en una colonia de cría de pájaros, ubicación de núcleos en una sección microscópica de tejido, depósitos de oro mapeados en un estudio geológico, estrellas en un cúmulo estelar, accidentes de tráfico, terremotos, llamadas de teléfonos móviles, avistamientos de animales o casos de una enfermedad rara.

Se llama patrón espacial de puntos a cualquier conjunto de datos de este tipo. La disposición espacial de los puntos es el principal foco de investigación. Son muchos los campos de la ciencia donde este tipo de estructuras son de interés; por ejemplo, en ecología, epidemiología, geociencia, astronomía, econometría e investigación criminal. El análisis estadístico de la disposición espacial de los puntos puede revelar características importantes, como que los yacimientos de oro suelen encontrarse cerca de una gran falla geológica o que los casos de una enfermedad son más frecuentes cerca de una fuente de contaminación.

El análisis de los datos de patrones de puntos ha proporcionado evidencia fundamental para importantes investigaciones, desde la transmisión del cólera hasta el comportamiento de los asesinos en serie y la estructura a gran escala del universo. Los puntos en un patrón de puntos pueden tener todo tipo de atributos. Un estudio forestal podría registrar cada ubicación, especie y diámetro del árbol; un catálogo de estrellas puede dar sus posiciones en el cielo, masas, formas y colores; las ubicaciones de los casos de enfermedades pueden estar vinculadas a registros clínicos detallados. Esta información auxiliar adjunta a cada punto en el patrón de puntos se llama marca y en ese caso se habla de un patrón de puntos marcado. La colección de localizaciones de un patrón puntual puede venir definida en una región plana (Sec. 43.2) o bien en una red lineal (Sec. 43.3), haciendo que las distancias dejen de ser euclidianas para pasar a ser del camino más corto. Esto introduce ciertos cambios metodológicos en cuanto a las construcciones de ciertas características, que en el caso de intensidades de primer orden se tratan en este capítulo.

43.2 Patrones puntuales espaciales en \(\mathbb R^2\)

La teoría de procesos puntuales espaciales constituye la base para el análisis de eventos observados geográficamente a través de sus coordenadas (longitud, latitud) en un espacio bi-dimensional. Esta rama de los procesos puntuales pertenece al campo de la estadística espacial en conjunción con la de procesos estocásticos. De hecho, un proceso puntual espacial es un proceso estocástico cuyas realizaciones consisten en un conjunto numerable de puntos en el plano (patrón puntual). Heurísticamente, se trata de un conjunto de datos que se encuentra en una región concreta (o área de estudio).

Sea \({\bf x} =\{ {\bf x}_1, {\bf x}_2, \ldots, {\bf x}_n \}, \hspace{0,1cm}0 \leq n < \infty\) una realización (patrón puntual) observada de un proceso puntual simple (i. e. sin múltiples eventos por localización) y finito \(X\) en \(\mathbb R^2\) en la región \(W \subset \mathbb R^2\) y con la métrica (distancia) asociada \(d(\bf u,\bf v)\), siendo \(\bf u\) y \(\bf v\) dos localizaciones espaciales en \(W\). En general, las realizaciones consisten en un conjunto numerable de puntos (llamados en muchas ocasiones eventos). Las Figs. 43.1 y 43.2 permiten ver algunos ejemplos de patrones puntuales. Para cualquier conjunto arbitrario \(A \subset \mathbb R^2\), el cardinal de \(X\) viene dado por la función de conteo:

\[\begin{equation*} N(X \cap A) = \sum\limits_{{\bf x} \in X} {\mathbf 1} \{ {\bf x} \in A \} < \infty , \end{equation*}\]

donde \(\mathbf 1\) es una función indicadora.

Además, como establece la fórmula de Campbell (Baddeley et al., 2015), para cualquier función medible \(f: \mathbb R^2 \to [0, \infty)\) se cumple que: \[\begin{equation*} \mathbb E \left[ \sum\limits_{{\bf x} \in X} f({\bf x}) \right] = \int_{\mathbb R ^2} f({\bf u}) \lambda({\bf u}) \mathrm{d} {\bf u}, \tag{43.1} \end{equation*}\] donde \(\lambda (\cdot)\) determina la función de intensidad de \(X\) y gobierna su distribución espacial. De hecho, \(\lambda({\bf u})\) proporciona el valor esperado de eventos por unidad de área en un entorno de \({\bf u} \in \mathbb R^2\). Teniendo en cuenta que \(f({\bf x}) = { 1} \{{ \bf x} \in A \}\), se puede observar fácilmente la relación entre la función de intensidad \(\lambda(\cdot)\) y la de conteo \(N\): \[\begin{equation*} \mathbb E \left[ N(X \cap A) \right] = \int_A \lambda({\bf u}) \mathrm{d} {\bf u}. \end{equation*}\] Si la función de intensidad \(\lambda(\cdot)\) es constante, i.e. \(\lambda(\cdot) = \lambda\), se dice que el proceso \(X\) es homogéneo, mientras que, en caso contrario, se dice que es inhomogéneo; en este último caso, la distribución espacial varía a lo largo de la región soporte (para el lector con un mayor interés en conceptos y desarrollos se aconseja consultar Møller & Waagepetersen (2003), Illian et al. (2008), Diggle (2013) y Baddeley et al. (2015).

En la práctica se suele observar solo una única realización y, por ello, es importante disponer de una estimación de \(\lambda(\cdot)\) que represente fielmente la distribución espacial del proceso subyacente que ha generado el patrón observado. A continuación se exponen diferentes estimadores no paramétricos de la intensidad.

43.2.1 Estimación de la intensidad basada en funciones núcleo

Dos estimadores no paramétricos de la función de intensidad ampliamente utilizados en patrones puntuales en \(\mathbb R^2\), basados en funciones núcleo, vienen dados por: \[\begin{equation} \widehat \lambda^{\text{U}}_{\sigma}({\bf u}) = \frac{1}{c_{\sigma,W}({\bf u})} \sum_{i=1}^n \kappa_{\sigma}({\bf u} - {\bf{x}}_i), \quad {\bf u} \in W \tag{43.2} \end{equation}\] y \[\begin{equation} \widehat \lambda^{\text{JD}}_{\sigma}({\bf u}) = \sum_{i=1}^n \frac{\kappa_{\sigma}({\bf u} - {\bf x}_i)}{c_{\sigma,W}({\bf x}_i)}, \quad {\bf u} \in W, \tag{43.3} \end{equation}\]

donde \(\kappa_{\sigma}\) es una función de densidad de probabilidad en \(\mathbb R^2\) con parámetro de suavizado (ancho de banda) \(\sigma\), y

\[\begin{equation} c_{\sigma,W}({\bf u}) = \int_W \kappa_{\sigma}({\bf u} - {\bf v}) \mathrm{d} {\bf v}, \quad {\bf u} \in W \end{equation}\] es el área del núcleo centrado en \({\bf u} \in W\), y equivale a un corrector de borde que compensa por la falta de información fuera de \(W\). Hay que recordar que, en la práctica, solo se observa una realización de \(X\) en la región acotada \(W\). Más allá de la elección de \(\sigma\), el estimador (43.2) es insesgado si la función de intensidad es constante (Diggle, 1985), mientras que el estimador (43.3) conserva la masa total (Jones, 1993). Los estimadores (43.2) y (43.3) suelen ser llamados “uniformly-edge-corrected” y “Jones-Diggle” (Rakshit, Davies, et al., 2019). En este capítulo, se considera en todo momento la función núcleo gaussiana (Silverman, 1986).

En términos prácticos, la adecuación de los estimadores basados en núcleos depende del parámetro de suavizado, de forma que un suavizamiento pequeño lleva a un sesgo bajo y una varianza alta, mientras que un parámetro de suavizado alto resulta en un sesgo alto y a una varianza pequeña. Para un determinado patrón puntual \({\mathbf x}\), los estimadores (43.2) y (43.3) pueden ser calculados utilizando la función density.ppp() de spatstat.core, especificando diggle=FALSE y diggle=TRUE, respectivamente.

43.2.1.1 Selección del parámetro de suavizado

Scott (1992) propuso elegir este parámetro a través de un regla un tanto naíf (llamada rule of thumb) de la forma: \[ (s_x n^{-1/6}, s_y n^{-1/6}), \] para cada coordenada cartesiana \(x,y\), donde \(s_x, s_y\) son las desviaciones típicas de las coordenadas (\(x,y\)) de los eventos. Este procedimiento es útil para análisis exploratorios. La función bw.scott() de spatstat.explore proporciona este estimador. Nótese que, en el caso de Scott, el parámetro de suavizado es, por construcción, un vector de dos componentes para suavizar ambas coordenadas cartesianas.

Cronie & Van Lieshout (2018) propusieron encontrar el parámetro óptimo minimizando: \[ CvL(\sigma) = \left( |W| - \sum\limits_{i=1}^n \frac {1} { \widehat{\lambda}^*_{\sigma}({\bf x}_i)} \right)^2, \]

donde \(|W|\) es el tamaño de la región \(W\) y \(\widehat{\lambda}^*_{\sigma}({\bf x}_i)\) es un estimador de la intensidad sin corregir (bien sea la expresión (43.2) o la expresión (43.3), pero sin el término de corrección) evaluado en \({\bf x}_i\) y con parámetro de suavizado \(\sigma\). La idea de este estimador proviene de la fórmula de Campbell, ya que: \[ \mathbb E \left[ \sum\limits_{x \in X} 1 / \lambda(x) \right] = \int_W (1 / \lambda(x) ) \lambda(x) \mathrm{d} u = |W|. \] Para un patrón puntual \({\mathbf x}\), la función bw.CvL() de spatstat.explore calcula el parámetro de suavizado mediante el método de Cronie y van Lieshout (se denotará por Cronie–van Lieshout).

43.2.2 Ejemplos prácticos

En esta sección se hace uso de los estimadores de la intensidad anteriormente mostrados y de los diferentes métodos de selección del parámetro de suavizado para analizar la distribución espacial de dos conjuntos de datos: incendios forestales en Nepal (Fig. 43.1), y eventos de crímenes en Medellín, Colombia (Fig. 43.2). Para ello, se utilizan las librerías spatstat, versión 2.3-0, (Baddeley et al., 2015; Baddeley & Turner, 2005) para el análisis de patrones puntuales y raster, versión 3.5-15, (Hijmans, 2022) para determinadas representaciones gráficas.

Nota

La librería spatstat ha sido recientemente dividida en una familia de sub-librerías spatstat.utils, spatstat.data, spatstat.sparse, spatstat.geom, spatstat.random, spatstat.core, spatstat.linnet, spatstat.explore, spatstat.model, de forma que spatstat actúa como una libería paraguas de todas ellas. Los lectores deben estar atentos a posibles futuros cambios en spatstat y raster para satisfacer ciertas restricciones de CRAN en relación con los tamaños de sus librerías.

43.2.2.1 Ejemplo 1: incendios forestales en Nepal

Por cortesía de Ganesh Prasad Sigdel, se dispone de localizaciones georreferenciadas de incendios forestales en Nepal durante 2016, datos cedidos por la institución ICIMOD-Nepal. En 2016, Nepal sufrió 5.757 incendios, de los cuales 475 ocurrieron en el distrito de Surkhet, en la provincia de Karnali, en el medio-oeste de Nepal. Se comienza llamando a algunas librerías de R, útiles para nuestros propósitos.

# library("raster")
# library("spatstat")
# library("CDR")

Utilizando los métodos descritos en la Sec. 43.2.1.1, se estima el correspondiente parámetro de suavizado. La regla de Scott proporciona los valores (50.253,47 m, 21.158,42 m) y el método de validación cruzada de Cronie–van Lieshout estima el valor como 36.513,16 m. Mediante el argumento ns de bw.CvL(), se puede controlar mejor la búsqueda del parámetro óptimo a través de un grid más fino.

data(nepal)
scott_nepal <- bw.scott(nepal) # Scott’s rule
CvL_nepal <- bw.CvL(nepal) # Cronie and van Lieshout’s criterio

Conocido el parámetro de suavizado, se estima la intensidad mediante los estimadores (43.2) y (43.3). La función density.ppp() proporciona una estimación basada en funciones núcleo para patrones en \(\mathbb R^2\), teniendo en cuenta que, por defecto, esta función hace uso del estimador con corrección uniforme para los bordes (uniformly-edge-corrected estimator) (43.2) con un núcleo gaussiano. Se fija leaveoneout=FALSE para no calcular el estimador leave-one-out, mientras que se establece positive=TRUE para forzar valores positivos en la densidad. Esto último obedece a que, debido a errores numéricos en el cálculo de la transformada rápida de Fourier, se pueden obtener valores negativos en ciertas áreas (véase la ayuda de density.ppp()).

d_scott_nepal <- density.ppp(nepal, sigma = scott_nepal, 
                             leaveoneout = FALSE, positive = TRUE)
d_cvl_nepal <- density.ppp(nepal, sigma = CvL_nepal, 
                           leaveoneout = FALSE, positive = TRUE)

La estimación de la intensidad mediante el estimador de Jones-Diggle (43.2) se lleva a cabo escribiendo diggle=TRUE en density.ppp():

d_scott_dig_nepal <- density.ppp(nepal, sigma = scott_nepal, 
                                 leaveoneout = FALSE, positive = TRUE, diggle = TRUE)
d_cvl_dig_nepal <- density.ppp(nepal, sigma = CvL_nepal, 
                               leaveoneout = FALSE, positive = TRUE, diggle = TRUE)

Tras obtener diferentes estimadores de la intensidad bajo diferentes métodos de selección del parámetro de suavizado, a continuación se muestran estas estimaciones y se comentan sus discrepancias. Para una mejor representación gráfica, se convierten las imágenes de intensidad dadas en la clase im a objetos de clase raster para luego juntarlas en un RasterStack. La Fig. 43.1 muestra estas estimaciones, observándose una mayor intensidad en el sur y suroeste de Nepal, indicando una clara distribución no uniforme de dicha intensidad, lo que, a su vez, indica un alto grado de inhomogeneidad.

sp_int_nepal <- stack(raster(d_scott_nepal), raster(d_cvl_nepal), raster(d_scott_dig_nepal), raster(d_cvl_dig_nepal))
sp_int_nepal <- sp_int_nepal * 10^7
names(sp_int_nepal) <- c("scott_gaus_U", "CvL_gaus_U", "scott_gaus_JD", "CvL_gaus_JD")

at <- c(seq(0, 1.4, 0.2))
pts_nepal <- as.data.frame(nepal)
coordinates(pts_nepal) <- ~ x + y
library("latticeExtra")
spplot(sp_int_nepal, at = at, scales = list(draw = FALSE), col.regions = rev(topo.colors(20)), colorkey = list(labels = list(cex = 3)), par.strip.text = list(cex = 3)) + layer(sp.points(pts_nepal, pch = 20, col = 1))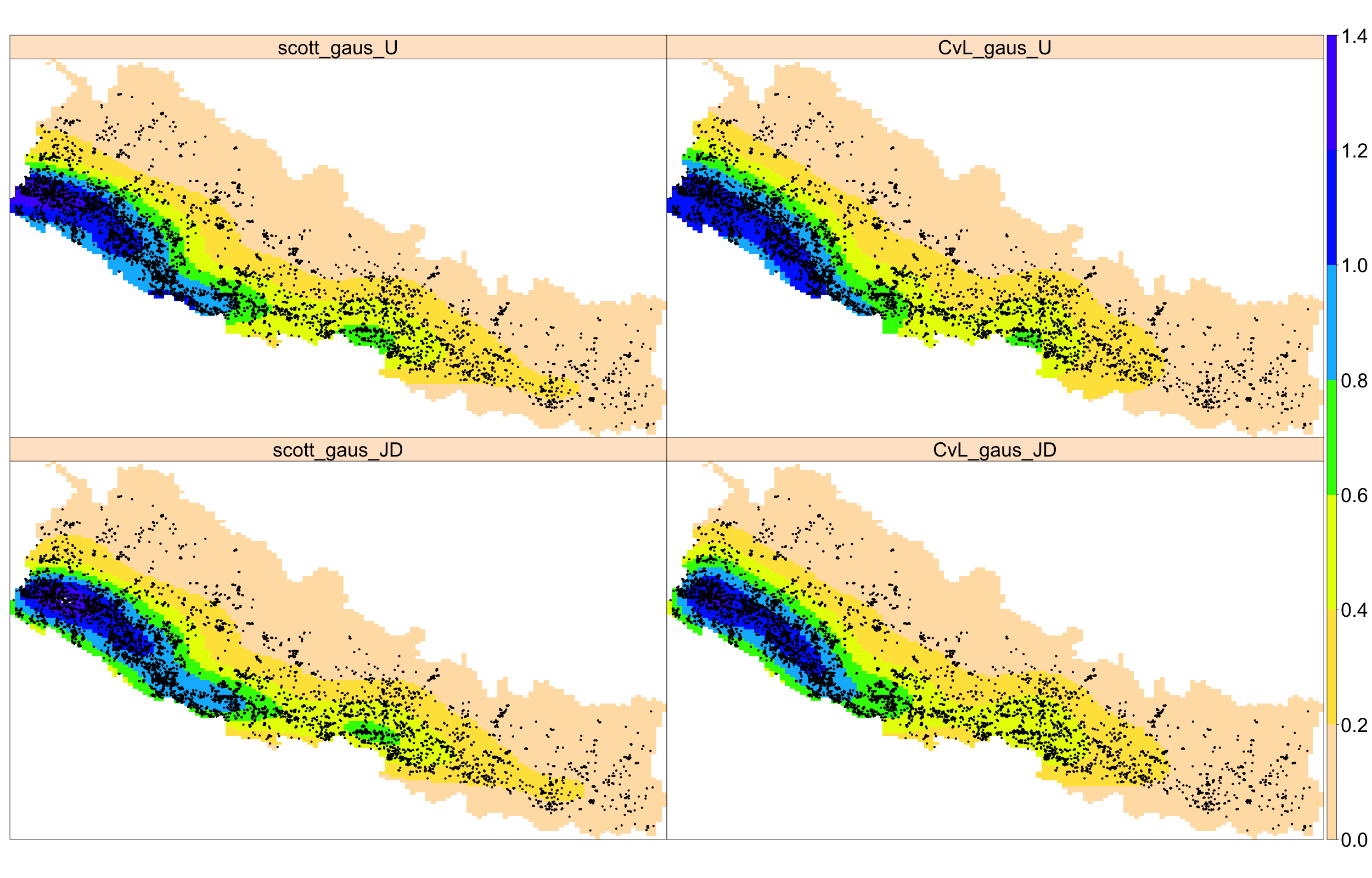

Figura 43.1: Estimación basada en funciones núcleo para los incendios forestales (puntos negros) en Nepal en 2016. Las etiquetas de los nombres comienzan con el método de suavizado, seguido del núcleo utilizado y de la corrección de borde. Los valores de la intensidad indican el número de incendios por 10.000 km2. Se usan JD y U para indicar los estimadores de Jones-Diggle y con corrección uniforme para los bordes, respectivamente.

43.2.2.2 Ejemplo 2: crímenes en Medellín

Medellín es la segunda ciudad con más población en Colombia (DANE, 2019), con un territorio urbano de \(105\) km\(^2\), que ha sufrido de múltiples acciones criminales durante muchos años, como es bien conocido. En 2018, la Secretaría de Seguridad de Medellín reportó que el \(40\%\) de los ciudadanos se sentía inseguro: a modo de ejemplo, en dicho año el número de quejas por robo se elevó a 20.607 (Restrepo, 2019). Adicionalmente, el departamento de policía reconocía la necesidad de contratar al menos 2.000 policías más para luchar contra los homicidios, robos y microtráfico (Monsalve, 2019).

En esta sección solo se analiza la distribución espacial de los eventos georreferenciados de crímenes ocurridos en Medellín durante 2005 (Sanabria et al., 2022). En 2005 ocurrieron 910 crímenes, de los cuales el porcentaje de víctimas varones fue del \(66\%\) y el \(28\%\) fueron cometidos durante los fines de semana; el porcentaje de robos fue del \(42\%\) y el de víctimas con edades entre 20 y 40 fue del \(60\%\).

Nótese que el conjunto de localizaciones donde ocurrieron estos crímenes no hace referencia necesariamente a las calles de la ciudad y, por tanto, se considera que el patrón puntual tiene como dominio de definición todo \(\mathbb R^2\).

data(medellin)
scott_med <- bw.scott(medellin) # Scott’s rule
CvL_med <- bw.CvL(medellin) # Cronie and van Lieshout’s criterio

La regla de Scott estima el parámetro de suavizado en (691,31 m, 954,20 m) mientras que el criterio de validación cruzada (CvL) lleva a un valor estimado de 692,31 m. Para obtener las distintas estimaciones de la intensidad (43.2) y (43.3) bajo los mismos escenarios que en la Sec. 43.2.2.1 se utiliza la función density.ppp()

d_scott_med <- density.ppp(medellin, sigma = scott_med,
                           leaveoneout = FALSE, positive = TRUE)
d_cvl_med <- density.ppp(medellin, sigma = CvL_med,
                         leaveoneout = FALSE, positive = TRUE)

d_scott_dig_med <- density.ppp(medellin, sigma = scott_med,
                               leaveoneout = FALSE, positive = TRUE, diggle = TRUE)
d_cvl_dig_med <- density.ppp(medellin, sigma = CvL_med,
                             leaveoneout = FALSE, positive = TRUE, diggle = TRUE)

La Fig. 43.2 muestra la intensidad estimada bajo diferentes parámetros de suavizado. Se observa, en general, una distribución no homogénea de los crímenes. Independientemente del método utilizado, se identifican dos grandes hotspots en la zona central de Medellín, aunque con diferentes magnitudes. El efecto de la corrección de borde es solo marginal.

sp_int_med <- stack(raster(d_scott_med), raster(d_cvl_med),
                    raster(d_scott_dig_med), raster(d_cvl_dig_med))
sp_int_med <- sp_int_med * 10^5
names(sp_int_med) <- names(sp_int_nepal)
at <- seq(0, 3, by = 0.2)
pts <- as.data.frame(medellin)
coordinates(pts) <- ~ x + y

sp::spplot(sp_int_med, at = at, scales = list(draw = FALSE),
           col.regions = rev(topo.colors(20)), colorkey = list(labels = list(cex = 3)),
           par.strip.text = list(cex = 3)) + layer(sp.points(pts, pch = 20))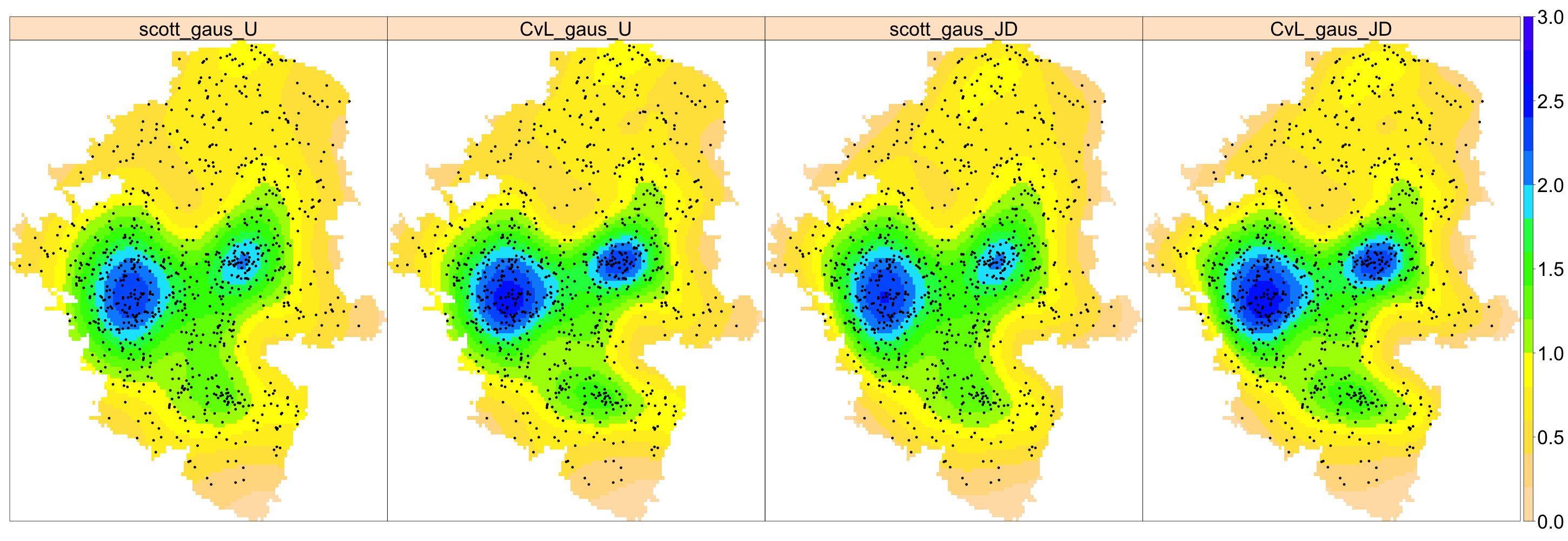

Figura 43.2: Estimación de la intensidad basada en funciones núcleo para los datos de Medellín (puntos negros) durante 2005. Las etiquetas de los nombres comienzan con el método de suavizado, seguido del núcleo utilizado y de la corrección de borde. Los valores de la intensidad indican el número de crímenes por 100 km2. Se usan JD y U para indicar los estimadores de Jones-Diggle y con corrección uniforme para los bordes, respectivamente.

43.2.3 Estimación de la intensidad basada en funciones núcleo en dominios irregulares

Los estimadores (43.2) y (43.3) pueden mostrar deficiencias importantes como no cumplir la condición de que la integral sea el número de puntos, sesgo cerca de las fronteras o presentar suavizamientos artificiales que lleven a resultados inverosímiles en ciertas ocasiones (Baddeley et al., 2022). Estos problemas son más aparentes en caso de dominios irregulares. Como remedio, Baddeley et al. (2022) propusieron estimar la intensidad vía una función núcleo-calor (heat kernel), que puede definirse como una densidad de probabilidad de transición de un movimiento browniano en \(W\) que respeta las fronteras. De hecho, su propuesta, denominada estimador de difusión, toma la forma: \[\begin{equation} \widehat \lambda_t ({\bf u}) = \sum\limits_{i=1}^n \kappa_t ({\bf u}|{\bf x}_i) , \tag{43.4} \end{equation}\] donde \(t= \sigma^2\) (\(\sigma\) es el parámetro de suavizado en las expresiones (43.2) y (43.3)) y \(\kappa_t (\cdot| {\bf x}_i)\) es el núcleo-calor. Este estimador es insesgado (baja homogeneidad) y preserva la masa (es decir, integra el número de puntos). Baddeley et al. (2022) proponen algunos nuevos métodos de selección del parámetro de suavizado, adaptados a su estimador de difusión, incluyendo el de Cronie–van Lieshout. El estimador de difusión se puede calcular con la función densityHeat.ppp(), y el criterio de Cronie–van Lieshout viene en la función bw.CvLHeat(). Todas estas funciones pertenecen al paquete spatstat.explore.

A continuación, a partir de un conjunto de datos de incendios activos en EE. UU. y América Central (sin considerar las islas) desde el 24 de febrero al 3 de marzo de 2022,²⁷⁴ se analiza el comportamiento del estimador de difusión en comparación con el estimador (43.2). Hay que hacer notar que las localizaciones, en este caso, no necesariamente confirman la existencia de un incendio, sino más bien píxeles susceptibles de existencia de incendio que han sido clasificados por medio de algoritmos preparados para ello. Este formato está relacionado con el contexto de datos en Near Real-Time (NRT).

Los parámetros de suavizado para los estimadores (43.2) y (43.4) siguen el criterio de Cronie–van Lieshout. Nótese que al tomar un área mucho más grande que en los ejemplos precedentes, se considera ns=50, es decir, se usa un vector de tamaño 50 para buscar el parámetro de suavizado óptimo (por defecto es 16), y dimyx=512 para obtener imágenes de intensidad con una mejor resolución (por defecto, las imágenes son de tamaño \(128\times 128\) píxeles). Los parámetros de suavizado elegidos para calcular (43.2) y (43.4) son 556,3 km y 104,9 km.

data(activefires)
CvL_northcentre <- bw.CvL(activefires, ns = 50)
d_CvL_northcentre <- density.ppp(activefires, sigma = CvL_northcentre,
                                 leaveoneout = FALSE, dimyx = 512)

heat_CvL_northcentre <- bw.CvLHeat(activefires, ns = 50)
dheat_CvL_northcentre <- densityHeat.ppp(activefires, sigma = heat_CvL_northcentre,
                                         leaveoneout = FALSE, dimyx = 512)

Ambas estimaciones se juntan en un objeto RasterBrick que se representa en la Fig. 43.3. Obsérvese que el dominio no es regular, pues los estados de Florida, California del Sur y América Central hacen que la región objeto de estudio sea ciertamente irregular. Esta irregularidad del dominio provocaría valores de intensidad totalmente irrealistas en dichas zonas. El mapa de intensidad que se muestra en el panel izquierdo de la Fig. 43.3 muestra que el estimador con corrección uniforme (uniformly-edge-corrected) distribuye la masa total por toda la región, provocando una sobresuavización. Sin embargo, el mapa del panel derecho, construido con el estimador de difusión, muestra una situación más realista, distribuyendo la masa de la intensidad acorde a los sucesos ocurridos.

d_northcentre_stack <- stack(raster(d_CvL_northcentre), raster(dheat_CvL_northcentre))
names(d_northcentre_stack) <- c("CvL_gaus_U", "Diffusion")
pts_northcentre <- as.data.frame(activefires)
coordinates(pts_northcentre) <- ~ x + y
d_northcentre_stack <- d_northcentre_stack * 10^6

spplot(d_northcentre_stack, scales = list(draw = FALSE),
       col.regions = rev(terrain.colors(20)), colorkey = list(labels = list(cex = 5)),
       par.strip.text = list(cex = 5)) +
  layer(sp.points(pts_northcentre, pch = 20, col = 1))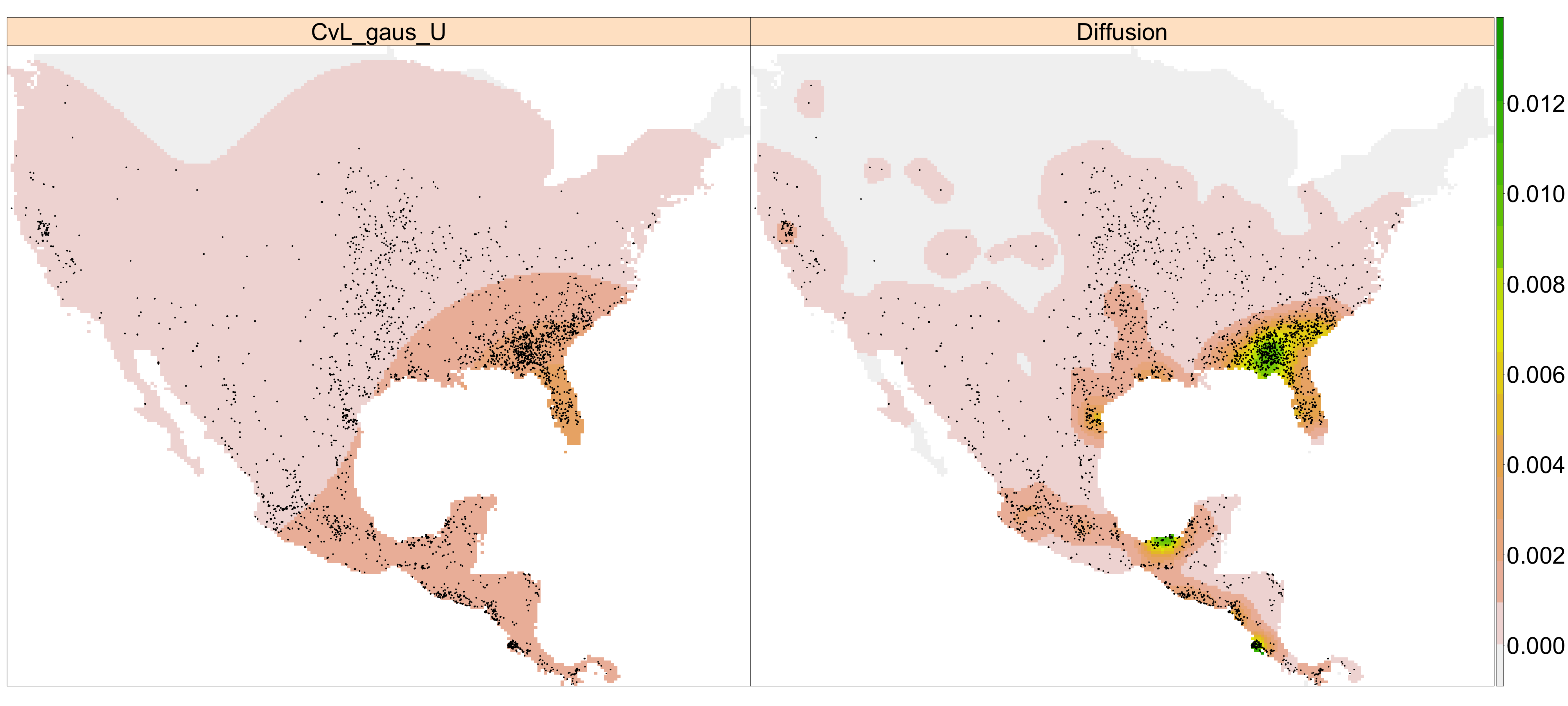

Figura 43.3: Estimación basada en función núcleo para incendios (puntos negros) en EE. UU. y Centroamérica (sin las islas) desde el 24 de febrero hasta el 3 de marzo de 2022. Izquierda: estimador con corrección uniforme con núcleo gaussiano. Derecha: estimador de difusión. El parámetro de suavizado fue obtenido con el criterio de Cronie–van Lieshout. Los valores de la intensidad son fuegos por 1.000 km2.

43.2.4 Estimadores basados en teselaciones de Voronoi

Como se ha visto, el comportamiento de los estimadores basados en funciones núcleo depende del parámetro de suavizado. Sin embargo, en situaciones en las que hay cambios abruptos en la distribución espacial de los puntos, un único valor constante de este parámetro no puede representar el suavizamiento necesario en toda la región. Para dar una solución a este problema, se propuso un parámetro con variación espacial (adaptable a la estructura espacial), aunque a costa de una mayor complejidad (Baddeley et al., 2022; Davies & Baddeley, 2018). Como alternativa a esta propuesta se pueden utilizar estimadores basados en teselaciones de Voronoi, que son no paramétricos (Barr & Schoenberg, 2010).

Para cada \({\bf x}_i\in{\mathbf x}\), su celda de Voronoi/Dirichlet \({\mathcal V}_{{\bf x}_i}\), consistente en todos los \({\bf u} \in W\) más cercanos a \({\bf x}_i\) que a cualquier otro elemento \({\bf x}_{\neq i}\in{\mathbf x}\setminus\{{\bf x}_i\}\), viene dada por: \[\begin{align} \mathcal V_{{\bf x}_i} = \{ {\bf u} \in W: d({\bf x}_i,{\bf u}) \leq d({\bf x}_{\neq i}, {\bf u}), \hspace{0,2cm} \forall {\bf x}_{\neq i}\in \mathbf{x}\setminus\{{\bf x}_i\} \}. \end{align}\]

El estimador basado en teselaciones de Voronoi, evaluado en cualquier punto arbitrario \({\bf u} \in W\), es de la forma:

\[\begin{align} \widehat{\lambda}^{V}({\bf u}) = \sum_{{{\bf x}_i}\in \mathbf{x}} \frac{\mathbf 1 \{ {\bf u}\in\mathcal V_{{\bf x}_i}\}}{\left | \mathcal V_{{\bf x}_i}\right|}. \tag{43.5} \end{align}\]

El estimador \(\widehat{\lambda}^{V}({\bf u})\) conserva la masa (al igual que \(\widehat \lambda^{\text{JD}}_{\sigma}({\bf u})\)) y es insesgado si la intensidad real es constante (igual que \(\widehat \lambda^{\text{U}}_{\sigma}({\bf u})\)), propiedades compartidas por el estimador de difusión. Sin embargo, Moradi et al. (2019) demostraron que \(\widehat{\lambda}^{V}({\bf u})\) tiene una varianza alta, lo que implica una infrasuavización en áreas densas de puntos y una sobresuavización en áreas con pocos puntos. Estos autores proponen corregir el problema de \(\widehat{\lambda}^{V}({\bf u})\) mediante un submuestreo de \(m \geq 1\) copias reescaladas \({\mathbf x}\) a través de adelgazamientos independientes con probabilidad \(p\) (independent \(p\)-thinning).²⁷⁵ Su propuesta viene dada por:

\[\begin{align} \widehat{\lambda}_{p,m}^{V}({\bf u}) = \frac{1}{m}\sum_{i=1}^m \frac{\widehat{\lambda}_i^{V}({\bf u})}{p} , \ {\bf u}\in W, \tag{43.6} \end{align}\] donde \(\widehat{\lambda}_i^{V}({\bf u})\) es el estimador de Voronoi del \(i\)-ésimo patrón adelgazado. Este nuevo estimador trata de forma más adecuada el equilibrio entre sesgo y varianza, que depende de la cantidad de puntos presentes en la subregión. Este efecto se consigue con muestras de menor tamaño procedentes del patrón original. El estimador \(\widehat{\lambda}_{p,m}^{V}({\bf u})\) se conoce como estimador de remuestreo-suavizado (resample-smoothed) y, además de las propiedades estadísticas de \(\widehat{\lambda}^{V}({\bf u})\), tiene una varianza bastante más pequeña. En este caso, también se debe seleccionar a priori (\(m,p\)); sin embargo, Moradi et al. (2019) proponen tanto una rule of thumb (\(m=400\) y \(p \leq 0,2\)) como una validación cruzada. Ambos estimadores (43.5) y (43.6) son accesibles por medio de la función densityVoronoi.ppp de spatstat.explore, y en la que los argumentos f y nrep controlan la probabilidad \(p\) y el número de adelgazamientos \(m\). Fijando f=1 se puede obtener el estimador basado en Voronoi (43.5).

A modo de ejemplo, se estima la intensidad de los incendios en Nepal (Sec. 43.2.2.1) mediante el método de estimador de remuestreo-suavizado de Voronoi (43.6) considerando diferentes probabilidades de retención para el adelgazamiento correspondiente.

d_vor_1_nepal <- densityVoronoi.ppp(nepal, f = 1, nrep = 1)
d_vor_2_nepal <- densityVoronoi.ppp(nepal, f = 0.8, nrep = 400)
d_vor_3_nepal <- densityVoronoi.ppp(nepal, f = 0.6, nrep = 400)
d_vor_4_nepal <- densityVoronoi.ppp(nepal, f = 0.5, nrep = 400)
d_vor_5_nepal <- densityVoronoi.ppp(nepal, f = 0.4, nrep = 400)
d_vor_6_nepal <- densityVoronoi.ppp(nepal, f = 0.2, nrep = 400)
d_vor_7_nepal <- densityVoronoi.ppp(nepal, f = 0.1, nrep = 400)
d_vor_8_nepal <- densityVoronoi.ppp(nepal, f = 0.05, nrep = 400)

Las estimaciones obtenidas, igual que las que proceden de density.ppp, son de clase im y se unen en un objeto RasterBrick para su representación gráfica.

sp_int_nepal_v <- stack(raster(d_vor_1_nepal), raster(d_vor_2_nepal), 
                        raster(d_vor_3_nepal), raster(d_vor_4_nepal), raster(d_vor_5_nepal),
                        raster(d_vor_6_nepal), raster(d_vor_7_nepal), raster(d_vor_8_nepal))
names(sp_int_nepal_v) <- NULL
names <- as.character(sort(c(seq(.2, 1, .2), 0.1, 0.05, 0.5), decreasing = TRUE))
names <- paste("p =", names)

sp_int_nepal_v <- sp_int_nepal_v * 10^7
at <- c(0, 0.3, 0.7, seq(2, 5, 1), 30)

spplot(sp_int_nepal_v, at = at, colorkey = list(labels = list(cex = 3)), 
       col.regions = topo.colors(20), scales = list(draw = FALSE), 
       par.strip.text = list(cex = 3), names.attr = names)

La Fig. 43.4 muestra las intensidades procedentes de los estimadores de remuestreo-suavizado de Voronoi para los incendios de Nepal y para diferentes probabilidades de retención. Se puede observar un menor suavizado y una mayor varianza para valores elevados de las probabilidades de retención \(p\). Asimismo, se puede ver que para probabilidades de retención menores que 0,2 el estimador proporciona mejores suavizados locales que los estimadores basados en suavizados fijos.

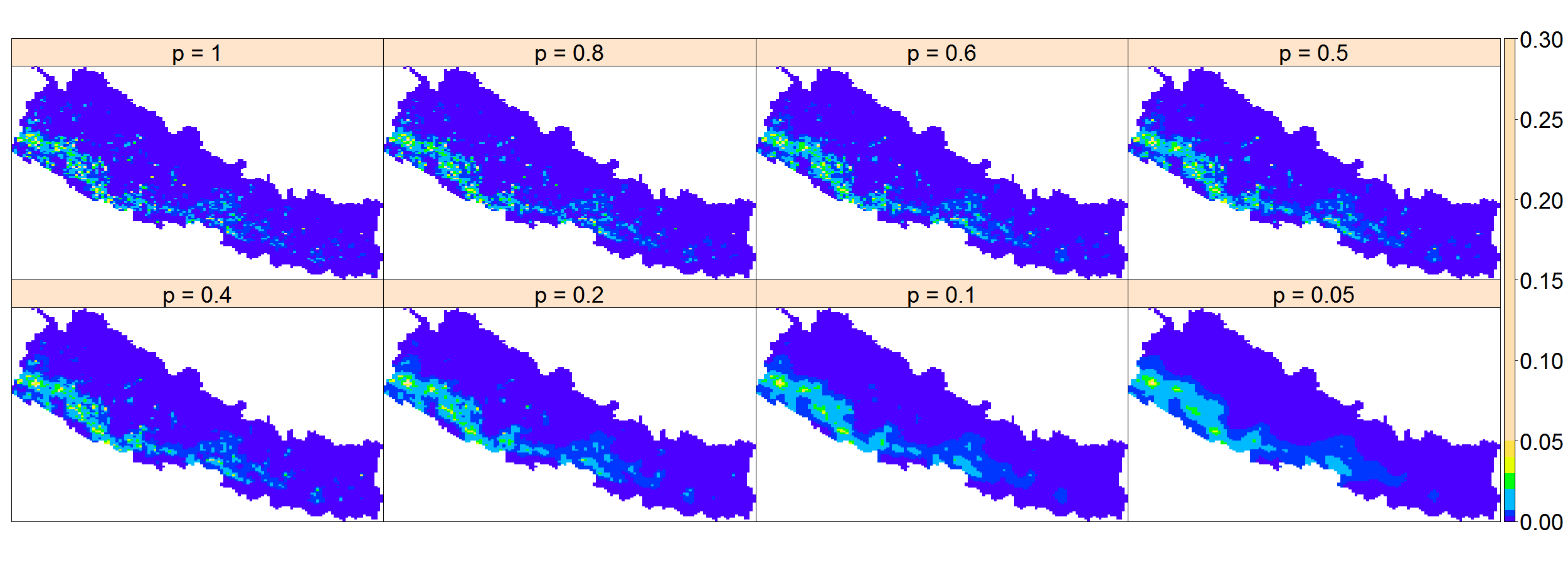
Figura 43.4: Estimaciones de la intensidad mediante estimadores de remuestreo-suavizado de Voronoi para los incendios en Nepal en 2016 con diferentes probabilidades de retención. La intensidad proporciona el número de incendios por 10.000 km2.

43.2.5 Características de segundo orden: la función \(K\) de Ripley

La función de intensidad presentada en las secciones anteriores proporciona el número esperado de puntos por unidad de espacio y no tiene en cuenta la estructura de dependencia entre dichos puntos. Esta estructura, sin embargo, viene caracterizada a través de lo que se llaman características de segundo orden. Las funciones de segundo orden determinan la estructura de dependencia espacial (o en su caso espaciotemporal, si interviene el tiempo) inherente al patrón puntual. La literatura ha propuesto varias funciones de segundo orden, de entre las cuales la función \(K\) de Ripley es posiblemnte la más utilizada. Esta función se define de forma pragmática como el número medio de eventos en un radio \(r\) alrededor de cualquier otro evento. Dicho de otra forma, la función \(K(r)\) representa el número medio de eventos dentro de un círculo de radio \(r\) alrededor de un evento típico del patrón (sin contar dicho evento central). De esta forma, \(K(r)\) describe características del proceso de puntos a muchas escalas (tantas como diferentes \(r\) se consideren). Esta función puede venir corregida por la intensidad de primer orden en el caso de procesos inhomogéneos. Ambas versiones de la función \(K\) vienen implementadas en spatstat a través de las funciones Kest() y Kinhom() para los casos homogéneo e inhomogéneo. Una propiedad interesante de esta función es que tiene una forma cerrada bajo el caso de aleatoriedad espacial completa, es decir, bajo la situación en la que el patrón de puntos es totalmente aleatorio, sin dependencia espacial alguna (llamado, en este caso, proceso de Poisson). Como bajo esta suposición \(K(r)=\pi r^2\), se puede contrastar si un cierto patrón es o no aleatorio construyendo bandas de confianza sobre la función \(K\) evaluada bajo simulaciones de aleatoriedad y evaluando la función \(K\) empírica procedente de los datos. La función envelope() permite construir tales intervalos de confianza.

También se han utilizado otras funciones para describir y contrastar patrones espaciales; estas funciones están basadas en la distribución de las distancias entre puntos que existiría en un patrón de Poisson, como, por ejemplo, la función de distribución de la distancia al vecino más próximo, la función de distribución de la distancia a un punto fijo aleatorio o la función \(J\), una combinación de las anteriores. Todas estas funciones, incluida la función \(K\), son en cierta forma funciones de distribución ya que, a cada escala o distancia \(r\), todos los pares de puntos separados por una distancia menor que \(r\) se usan para estimar el valor de la correspondiente función. En ocasiones puede ser necesario disponer de una función que caracterice el patrón de puntos de forma no acumulativa, es decir, que tenga en cuenta tan solo los pares de puntos que se encuentran separados por una distancia exactamente igual o similar a la distancia \(r\). La función de correlación de par \(g(r)\) (pair correlation function) es la herramienta apropiada en este caso (Baddeley et al., 2015).

A continuación se retoman los ejemplos de los incendios en Nepal y los delitos en Medellín para mostrar el código y los resultados de llevar a la práctica la estimación de la funcion \(K\) (inhomogénea) y la construcción de los correspondientes intervalos de confianza bajo el supuesto de aleatoriedad (véase Fig. 43.5).

d_nepal <- density.ppp(nepal, bw.scott, leaveoneout = TRUE)
en_nepal <- envelope(nepal, fun = Kinhom, correction = "border", nsim = 99, 
                     simulate = expression(rpoispp(d_nepal)), 
                     sigma = bw.scott, normpower = 2)

d_med <- density.ppp(medellin, bw.scott, leaveoneout = TRUE)
en_med <- envelope(medellin, fun = Kinhom, correction = "border", nsim = 99, 
                   simulate = expression(rpoispp(d_med)), 
                   sigma = bw.scott, normpower = 2)

en_nepal$mmean <- NULL
plot(en_nepal, main = "", lwd = 3, cex.axis = 2.5, cex.lab = 2.5, legend = FALSE)

en_med$mmean <- NULL
plot(en_med, main = "", lwd = 3, cex.axis = 2.5, cex.lab = 2.5, legend = FALSE)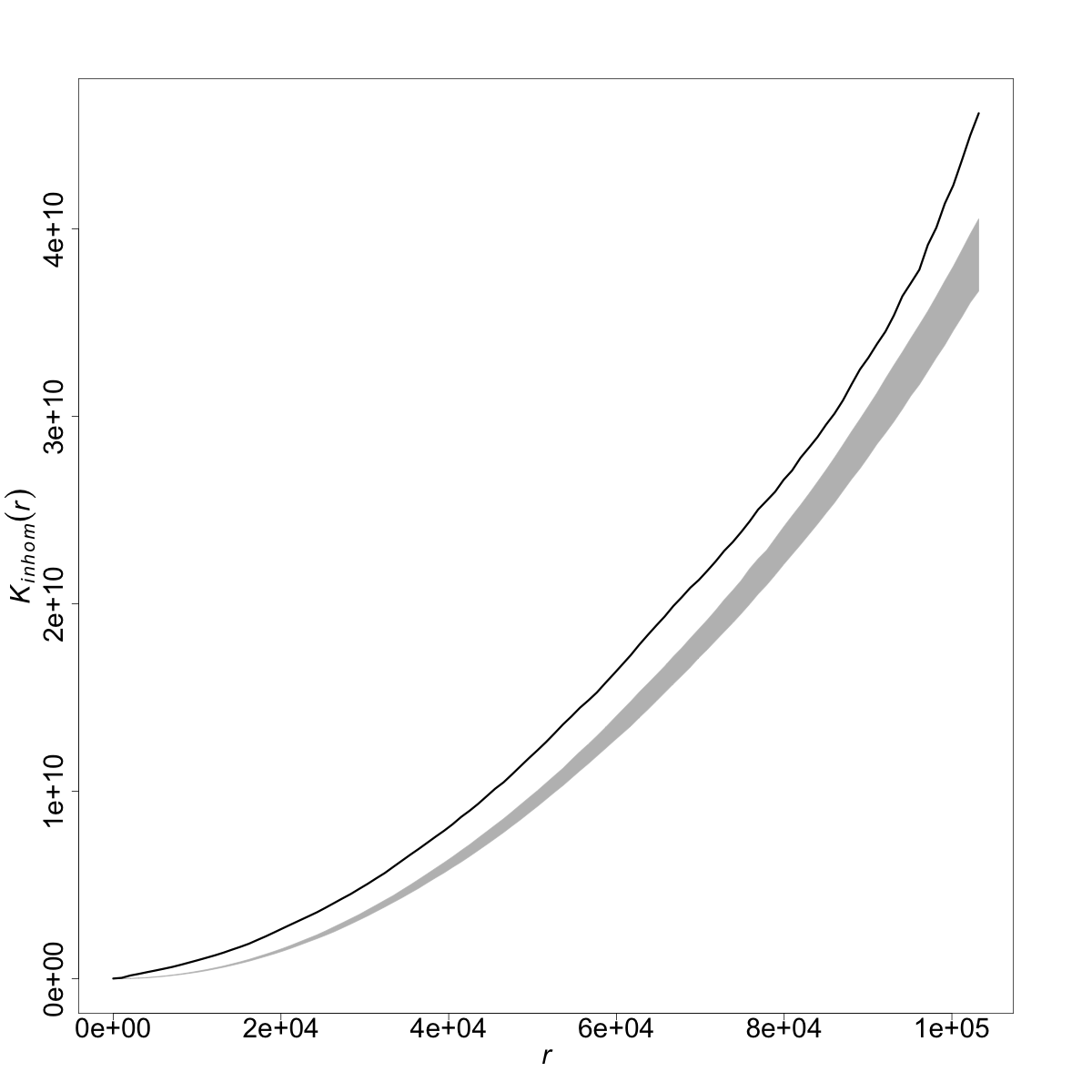

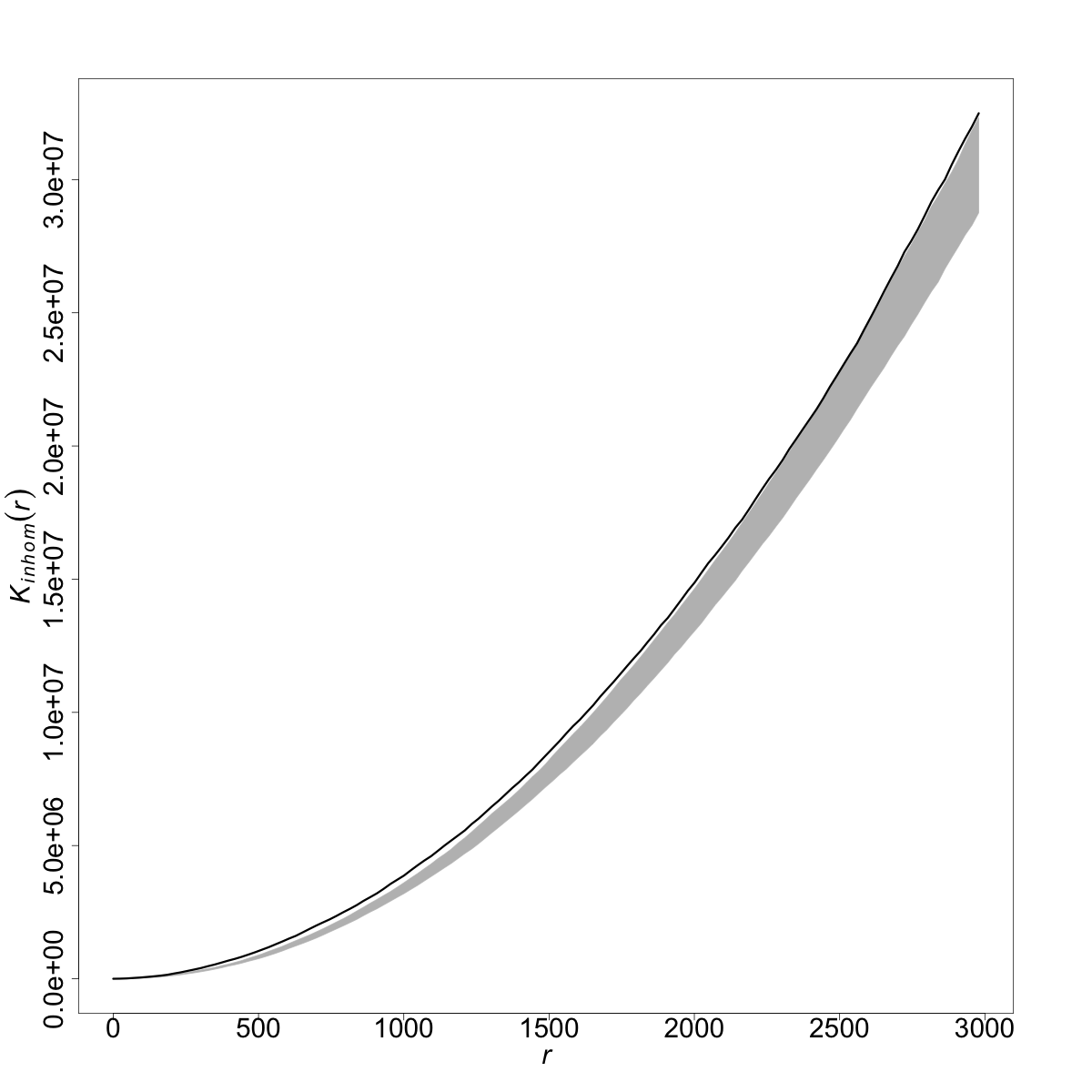
Figura 43.5: Funciones \(K\) de Ripley para incendios en Nepal y delitos en Medellín.

43.3 Patrones puntuales espaciales sobre redes lineales

En los últimos diez años, los patrones de puntos en redes lineales han recibido mucha atención científica. Una red lineal es un conjunto de segmentos (o aristas) unidos por nodos con un formato lineal, como una combinación convexa entre dos nodos. La explicación inicial detrás de la consideración de redes lineales como espacios de estado de algunos procesos puntuales podría estar en el hecho de que los objetos definidos en tales estructuras no pueden usar todo el espacio, y sus movimientos dependen fuertemente de su libertad sobre tales estructuras (Okabe & Sugihara, 2012). En consecuencia, entre otras cosas, la distribución espacial de los puntos, así como la correlación entre ellos, debe estudiarse con respecto a la red subyacente. Sin embargo, no ha sido tan fácil lidiar con este cambio de soporte cuando se pretende adaptar metodologías estadísticas existentes al análisis de patrones de puntos en redes lineales. Los principales desafíos no fueron solo matemáticos/estadísticos, sino también computacionales (Baddeley et al., 2021; Moradi, 2018).

Una red lineal es una unión de segmentos de línea \(l_i=[u_i,v_i]=\{tu_i + (1-t)v_i:0\leq t\leq 1\} \subset \mathbb R^2\). La métrica más común sobre dicha estructura fue inicialmente la distancia de ruta más corta (shortest-path distance) \(d_L({\bf u}, {\bf v})\), aunque más tarde Rakshit et al. (2017) propusieron otros tipos de distancias, incluida la euclidiana. La idea es que moverse por la red de segmentos implica respetar la geometría de dicha red y, por tanto, las líneas rectas (que sería el caso al usar distancias euclidianas) no son adecuadas. La distancia de ruta más corta sí que permite adaptarse a esta geometría. Sea \(Y\) un proceso puntual en una red lineal \(L\); entonces, la fórmula de Campbell (43.1) se adapta como sigue: \[\begin{equation*} \mathbb E \left[ \sum\limits_{y \in Y} f(y) \right] = \int_{L} f({\bf z}) \lambda(´{\bf z}) \mathrm{d}_1 {\bf z}, \end{equation*}\] donde \(\mathrm{d}_1\) denota integración con respecto a la longitud de arco. En este caso, \(\lambda({\bf z})\) proporciona el número esperado de puntos por unidad de longitud de \(L\) en una vecindad de \({\bf z} \in L\). Se han desarrollado distintos estimadores de la intensidad para patrones en redes considerando métricas adecuadas y resolviendo ciertos obstáculos matemáticos. El lector puede consultar más detalles al respecto en Moradi (2018) y Baddeley et al. (2021); en particular, se recomienda leer sobre el método de estimación no paramétrica basado en convoluciones bidimensionales de Rakshit, Davies, et al. (2019). Dada una realización \({\mathbf y}= \{ {\bf y}_1, {\bf y}_2, \ldots, {\bf y}_n \}\) de un proceso puntual \(Y\) sobre una red lineal \(L\), estos autores propusieron: \[\begin{equation} \widehat{\lambda}^\text{U}_{\sigma}({\bf z}) = \frac{1}{c_{\sigma,L}({\bf z})} \sum_{i=1}^{n} \kappa_{\sigma}({\bf z}-{\bf y}_i), \qquad {\bf z} \in L, \tag{43.7} \end{equation}\] con una corrección uniforme, y

\[\begin{equation} \widehat{\lambda}^\text{JD}_{\sigma}({\bf z}) = \sum_{i=1}^{n} \frac{ \kappa_{\sigma}({\bf z}-{\bf y}_i) }{ c_{\sigma,L}({\bf y}_i) }, \qquad {\bf z} \in L, \tag{43.8} \end{equation}\] con la corrección de Jones-Diggle, donde \(\kappa_{\sigma}\) es una función núcleo bivariante con suavizado \({\sigma}\), y \[\begin{equation*} c_{\sigma,L}({\bf z})=\int_L \kappa_{\sigma}({\bf z}- {\bf v}) \mathrm{d}_1 {\bf v} \end{equation*}\] es una corrección de borde.

Los dos estimadores anteriores tienen propiedades estadísticas similares a las de sus análogos para patrones de puntos espaciales en \(\mathbb R^2\) (es decir, los estimadores (43.2) y (43.3)) y sus estimaciones se pueden calcular rápidamente incluso en redes grandes y para grandes anchos de banda (parámetros de suavización). El cálculo rápido se logra mediante la transformada rápida de Fourier (Silverman, 1982). Además, Rakshit, Davies, et al. (2019) propusieron utilizar las versiones adaptadas de la regla de Scott, a la cual se puede acceder a través de la función bw.scott.iso() de spatstat.linnet, para obtener un ancho de banda óptimo. Nótese que el cálculo rápido de los valores de los estimadores anteriores simplifica aún más el cálculo de los valores de los estimadores de intensidad basados en el núcleo adaptativo y el riesgo relativo sobre las estructuras de red (Rakshit, Davies, et al., 2019).

También se recuerda que Moradi et al. (2019) propusieron su enfoque de submuestreo basado en Voronoi para procesos de puntos generales; para patrones de puntos en redes lineales puede calcularse mediante la función densityVoronoi.lpp() de spatstat.linnet.

Como ejemplo práctico para esta sección, se estudia la distribución espacial de delitos callejeros en Valencia. Valencia es la tercera ciudad más grande de España, siendo la capital de la Comunidad Valenciana. El territorio urbano de Valencia encierra un área de 134.65 km\(^2\), con más de 800.000 habitantes en el municipio. El conjunto de datos consta de las ubicaciones de 90.247 delitos callejeros como agresión (55.610 casos), robo (25.342 casos), robo contra la mujer con violencia (454 casos) y otros tipos de delitos (8.841 casos). Estos delitos se cometieron entre 2010 y 2020. Sin embargo, en lo que sigue, el análisis únicamente se centra en los datos correspondientes al año 2020, 6.868 casos, de los cuales 4.077 son agresiones, 2.060 son robos y 66 se relacionan con delitos contra la mujer con violencia.²⁷⁶

A continuación se estima el parámetro de suavizado utilizando la regla general de Scott (téngase en cuenta que ahora solo se considera una dimensión). El valor de la estimación es 584,1 m. La función densityQuick.lpp() de spatstat.linnet se usa para obtener el valor de los estimadores (43.7) y (43.8), teniendo en cuenta que por defecto esta función de spatstat usa el estimador de borde uniforme corregido (43.7).

data(valencia)
scott_valencia <- bw.scott.iso(valencia) # Scott rule
d_scott_valencia <- densityQuick.lpp(valencia, sigma = scott_valencia, 
                                     leaveoneout = FALSE, positive = TRUE, dimyx = 512)
d_scott_valencia <- d_scott_valencia * 1000

Las imágenes obtenidas son de tipo linim, y se convierten en objetos de clase im antes de pasarlas a objetos raster.

par(mfrow = c(1, 2))
plot(valencia$domain$window, lwd = 4)
plot(valencia, pch = 20, main = "", lwd = 4, cex = 1, add = T, 
     cols = "red", col = "blue")
plot(raster(as.im(d_scott_valencia)), main = "", axis.args = list(cex.axis = 4), 
     legend.width = 2, zlim = c(0, 6))
plot(valencia$domain$window, add = TRUE, lwd = 4)
par(mfrow = c(1, 1))

La Fig. 43.6 muestra la intensidad estimada junto con los eventos de delitos. Dicha intensidad identifica las zonas central y norte de la ciudad de Valencia como áreas de alto riesgo junto con otras zonas de bajo riesgo como son el este y la costa de la ciudad.

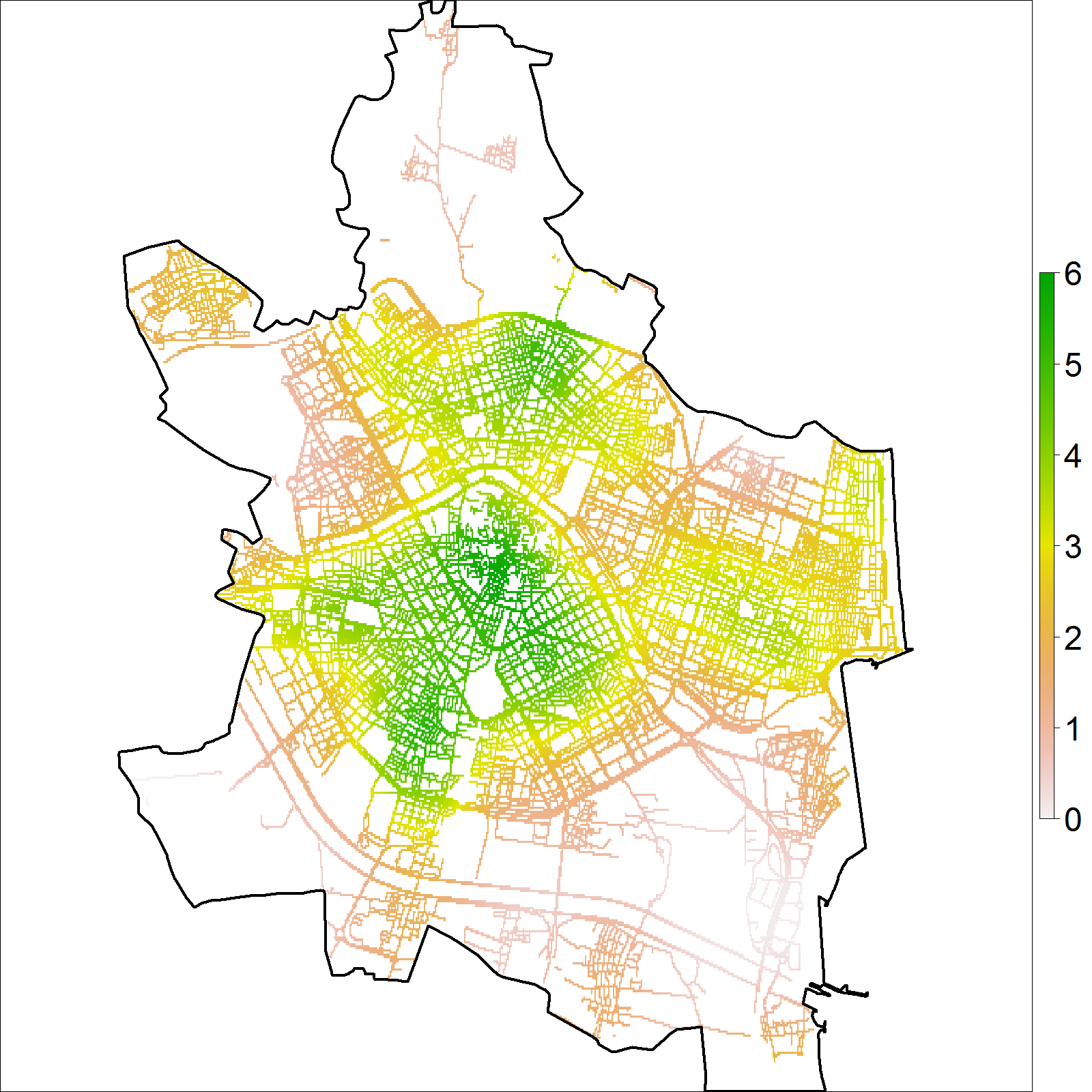
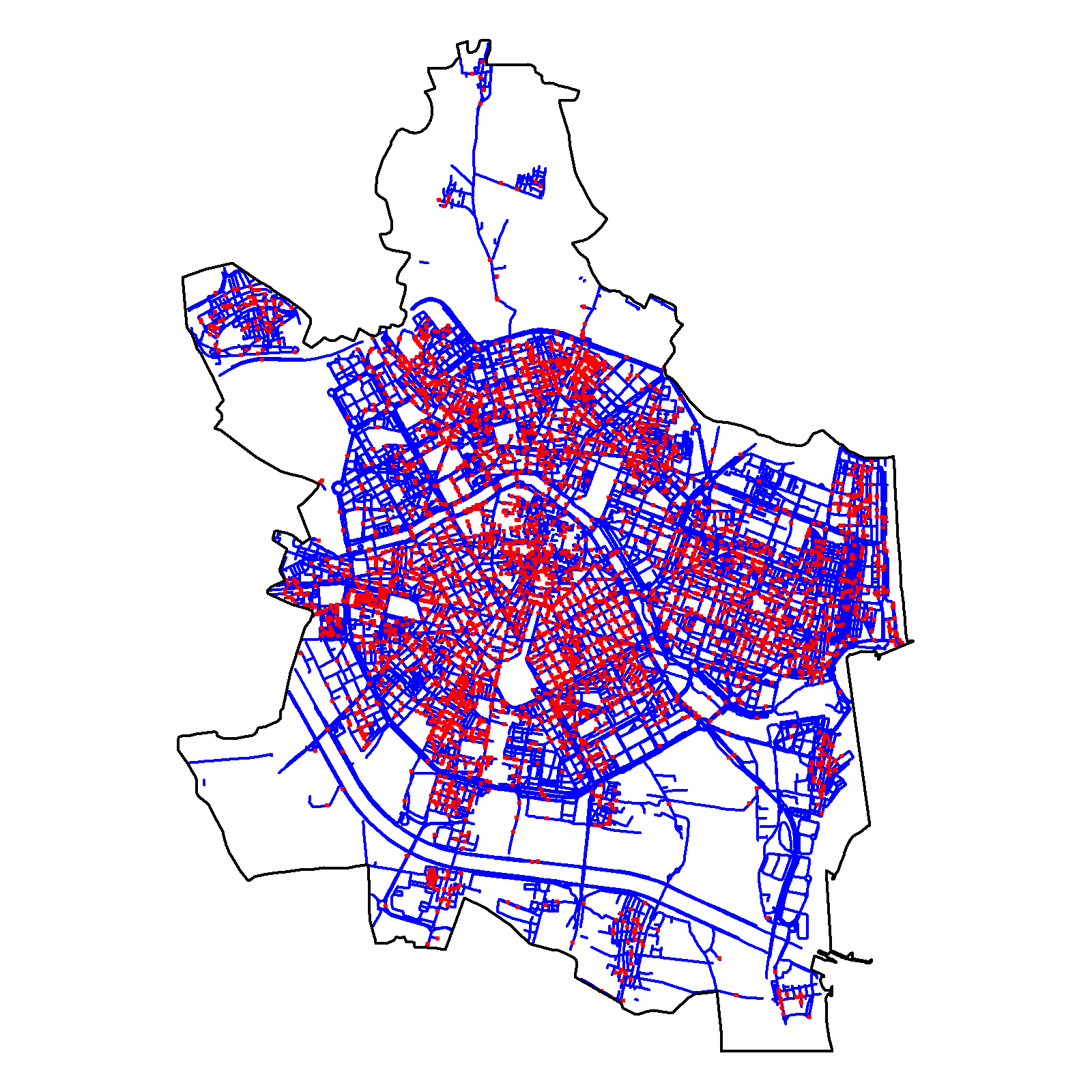
Figura 43.6: Intensidad estimada por función núcleo, usando el estimador de borde uniforme corregido (izquierda), para los datos de delitos (puntos rojos) en Valencia durante 2020 (derecha). Los valores de intensidad muestran el número de crímenes por km lineal.

d_vlc <- densityQuick.lpp(valencia, sigma = scott_valencia, leaveoneout = TRUE, 
                          positive = TRUE, at = "points", dimyx = 512)
d_vlc_im <- densityQuick.lpp(valencia, sigma = scott_valencia, leaveoneout = TRUE, 
                             positive = TRUE, dimyx = 512)

Finalmente, se muestra la función \(K\) de Ripley y el intervalo de confianza bajo un proceso de Poisson en una red lineal (véase la Fig. 43.7 y las siguientes referencias: Ang et al., 2012; Rakshit, Baddeley, et al., 2019). Se observa que la función \(K\) empírica cae dentro de las bandas, lo que indica que el tipo de delitos considerados, en 2020, es compatible con un proceso aleatorio. Obsérvese que al no considerar el tiempo, se pueden detectar clústeres espaciales que no existen en realidad, pues desaparecerían con la evolución temporal.

sim_vlc <- rpoislpp(lambda = d_vlc_im, L = net_vlc, nsim = 199)
library(spatstat.Knet)
K_vlc <- Knetinhom(valencia, lambda = as.numeric(d_vlc))
r <- K_vlc$r

K_sim <- lapply(X = 1:199, function(i) {
  sigma <- bw.scott.iso(sim_vlc[[i]])
  lambda <- densityQuick.lpp(sim_vlc[[i]], sigma = sigma, leaveoneout = TRUE, 
                             positive = TRUE, at = "points", dimyx = 512)
  Ksim <- Knetinhom(sim_vlc[[i]], lambda = as.numeric(lambda), r = r)
  return(Ksim)
})

K_nsim_df <- as.data.frame(do.call(cbind, d_nsim))
K_nsim_df_est <- K_nsim_df[, seq(3, 399, by = 2)]

maxn <- function(n) function(x) order(x, decreasing = TRUE)[n]
minn <- function(n) function(x) order(x, decreasing = FALSE)[n]

Kmin <- apply(K_nsim_df_est, 1, function(x) x[minn(5)(x)])
Kmax <- apply(K_nsim_df_est, 1, function(x) x[maxn(5)(x)])

plot(r, Kmin, type = "n", col = "grey", ylim = c(0, 270), 
     xlab = "r", ylab = expression(italic(K[inhom])))
points(r, Kmax, type = "n", col = "grey")
polygon(c(r, rev(r)), c(Kmax, rev(Kmin)), col = "grey", border = "grey")
points(r, K_vlc$est, type = "l")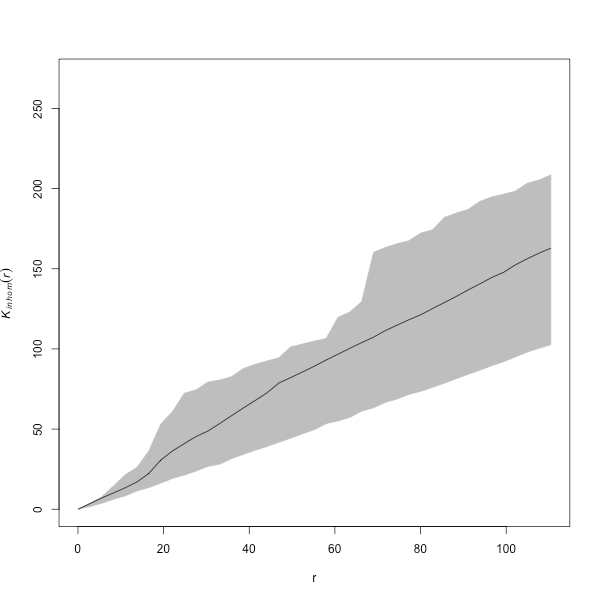

Figura 43.7: Función \(K\) para los delitos en Valencia (2020) junto con la envoltura bajo un proceso de Poisson.

Resumen

• La teoría de procesos puntuales espaciales constituye la base para el análisis de eventos observados geográficamente a través de sus coordenadas (longitud y latitud) en un espacio bidimensional. Esta es una de las ramas del campo de la estadística espacial en conjunción con la de procesos estocásticos. De hecho, un proceso puntual espacial es un proceso estocástico cuyas realizaciones consisten en un conjunto numerable de puntos (llamados en muchas ocasiones eventos). Heurísticamente, se trata de un conjunto de datos que se encuentra en una región concreta (área de estudio). Los puntos pueden representar cualquier población espacialmente explícita, como localizaciones de animales, nidos de aves, epicentros de terremotos, galaxias, crímenes, etc.

• El modelo estadístico más conocido para el análisis de patrones puntuales espaciales es el proceso puntual espacial de Poisson (asociado a la condición de aleatoriedad espacial completa). A partir del modelo de Poisson se construyen modelos más complejos.

• La modelización pasa por determinar las intensidades de primer y segundo orden que caracterizarán las propiedades básicas del comportamiento de los puntos. En este capítulo se proponen varios estimadores de la función de intensidad de primer orden junto con sus elementos asociados relacionados con funciones núcleo, parámetro de suavizado y correcciones de borde. Se consideran también algunos aspectos de medidas de segundo orden. El capítulo finaliza con algunas cuestiones sobre el cambio de soporte del plano euclídeo a redes lineales.